基于AGEP-DNN 的水下聚能装药比冲量预测模型

刘 芳郝慧敏卢 熹郭策安

(1.沈阳理工大学a.理学院，b.自动化与电气工程学院，c.装备工程学院，沈阳 110159；2.辽宁省兵器工业智能优化与控制重点实验室，沈阳 110159)

比冲量是爆炸过程中冲击波超压在正压作用时间上的积分，冲击波产生的峰值超压越高或正压作用时间越长，释放的能量越强大[1－2]。 比冲量是评估装药威力和爆炸能量的重要参数，智能、精准地预测比冲量数值对评估装药的作战效能具有重要意义。

目前，针对水下聚能装药比冲量预测的研究主要有仿真实验和经验公式两种方法。 仿真实验法利用仿真软件研究爆炸过程，能够节省真实实验成本[3－5]，但仿真时间长，不适用于信息化、智能化、快速反应的战场需求；经验公式法通常针对文献[6]提出的装药比冲量计算公式进行改进，采用改进公式预测不同装药质量和测距位置的比冲量[7]，但该方法不适用于装药结构参数变化的情况，算法泛化性较弱。

智能、准确地挖掘装药结构参数和比冲量数值之间的复杂非线性关系是装药结构设计和装药毁伤评估亟待解决的问题。 现已有研究人员利用神经网络的非线性映射能力对装药参数与爆炸载荷数据进行预测，奠定了装药毁伤参数智能预测算法的研究基础[8－9]。 由于神经网络易陷入局部最优且存在网络结构选择多样性问题，其在预测精度方面受到局限。

针对水下聚能装药比冲量预测中存在的泛化性弱、预测精度低、智能化欠缺的问题，本文基于聚能装药水下爆炸的仿真实验数据，提出一种自适应基因表达式编程(adaptive gene expression programming，AGEP)优化深度神经网络(deep neural network，DNN)[10]结构的比冲量预测模型，称为AGEP-DNN 模型。 使用DNN 挖掘水下爆炸过程中装药结构与不同爆距比冲量的非线性关系；构建基因表达式编程(gene expression programming，GEP)算法，优化DNN 的隐藏层层数和隐藏层节点数；设计自适应交叉概率和自适应变异概率，智能调节GEP 算法的搜索范围。 采用包含群智能算法优化三层BP 神经网络、卷积神经网络(CNN)、循环神经网络和GEP 优化DNN 的四大类9 种智能预测模型进行对比实验，验证本文AGEP-DNN 预测模型的有效性。

1 水下爆炸数值仿真

聚能战斗部水下爆炸产生的载荷与爆破战斗部相比，能量分配以及演化规律更加复杂[11]。 考虑到水下爆炸过程中参数获取困难，本文使用AUTODYN 软件进行聚能装药水下爆炸仿真实验，装药材料为B 炸药，药型罩为球缺结构，装药结构如图1 所示。 图中:R1和R2分别为球缺药型罩的外径和内径，R1＝52.5 mm，R2＝49.6 mm；l和d分别为装药长度和装药直径，l＝100 mm，d＝100 mm。 图中数值单位为mm。

图1 聚能装药结构Fig.1 Shaped charge structure

为研究装药结构参数和比冲量数值之间的非线性关系，仿真实验中假设装药类型、壳体材料、水介质等条件均不改变，只选取装药结构参数作为可变条件参数，研究不同爆距的比冲量分布情况。 为消除不同参数量纲的影响，选取无量纲化的药柱长径比l/d、相对轴向距离h/d和相对径向距离r/d三个结构参数对相对比冲量I/d进行预测研究，其中h和r分别表示测点距药柱前端面的轴向距离和测点距轴线的径向距离，I为比冲量。 水下爆炸聚能装药仿真模型及36 个测点位置如图2 所示，仿真实验中水体(WATER)、B 炸药(COMP B)、空气(AIR)和药型罩(COPPER)部分采用欧拉算法计算。

图2 聚能装药仿真模型及测点位置示意图Fig.2 Simulation model of shaped charge and schematic diagram of measurement point

为验证仿真数据的可用性，采用经验公式[6]计算比冲量，计算结果与仿真实验所得数据相对误差不超过15%，表明该仿真模型可靠性较高，可使用其数据对比冲量进行预测。 部分仿真实验数据与经验公式计算结果的对比如表1 所示。

表1 部分仿真实验数据和经验公式计算结果的对比Table 1 Comparison of partial simulation data and empirical formula results

2 比冲量预测模型

2.1 深度神经网络

考虑聚能装药水下爆炸比冲量预测问题涉及多种条件参数，具有高度的非线性，使用三层神经网络很难满足要求。 本文利用具有强大非线性挖掘能力的DNN 建立装药结构参数和比冲量之间的函数映射关系，提升预测精度。 模型网络结构如图3 所示，包含输入层、输出层和多个隐藏层，分为前向传播和反向传播两个过程。

图3 DNN 水下聚能装药比冲量预测模型网络结构Fig.3 Network structure of DNN underwater shaped charge specific impulse prediction model

在前向传播中，输入装药长径比、相对轴向距离和相对径向距离，通过隐藏层传输，对复杂物理化学过程进行拟合，输出网络预测后的相对比冲量。 为增加DNN 对非线性过程的拟合能力，缓解梯度消失问题，设置激活函数为ELU 函数，各层节点取值如式(1)所示。

为衡量预测值与真实值之间的误差，选取均方根误差(RMSE)作为网络的损失函数，其计算式为

式中:yi为真实值；为预测值；n为预测值个数。在反向传播中，使用梯度下降法根据RMSE 值对层间的权重和阈值进行调整。 进行正向和反向传播训练，直至满足最小误差为止。

2.2 自适应基因表达式编程

GEP 算法使用简单编码解决复杂问题，具有较大搜索范围和良好的计算精度[12]。 GEP 主要优化过程包括染色体编码与解码、适应度函数确定和种群遗传操作三个部分。 由于GEP 算法易陷入局部最优，本文设计改进的自适应遗传操作，扩大算法的搜索范围。

2.2.1 染色体编码与解码

GEP 中的染色体可含有单个或多个基因，每个基因有头部、尾部和常数(DC)域三部分，DC 域用于填充头部和尾部的问号，增加表达式的随机性，扩大基因的搜索范围。 预设头部长度的数值，则尾部长度的计算方法如式(3)所示。

式中:T和H分别为尾部和头部的长度；N为函数符允许的最多参数个数。

以一个二基因的染色体为例，描述其编译过程，如图4 所示。

图4 染色体编译过程Fig.4 Chromosome compilation process

2.2.2 适应度函数确定

适应度函数表示染色体对环境的适应能力，其设定会直接影响GEP 的进化过程。 为实现GEP 对DNN 结构的高效优化，本文采用DNN 的目标函数RMSE 作为GEP 的适应度函数，其值越小，说明模型预测精度越高。

2.2.3 种群自适应遗传操作

当染色体适应度不满足设定值时，种群将进行一系列遗传操作，主要包括选择、交叉和变异。传统GEP 算法中选择操作使用轮盘赌法，交叉操作和变异操作如图5 所示，图5(a)中虚线框为交叉的部分，图5(b)中下划线为变异的部分。

图5 染色体的交叉和变异Fig.5 Cross and variation of chromosomes

由图5 可知:交叉操作优化染色体，产生新结构，扩展种群搜索范围；变异操作改变基因位点，保护种群多样性，收敛寻优区间的范围。 传统GEP 算法的交叉率和变异率固定，交叉操作和变异操作没有区分优良个体和劣质个体在种群进化中的作用，不考虑进化过程，不能较好满足种群进化需求。 针对传统GEP 算法的交叉率和变异率固定不变的问题，充分考虑不同时刻基因进化的不同需求，将表征进化进程的迭代次数引入公式，改进GEP 算法的交叉率和变异率，如式(4)和式(5)所示。

式中:pc和pm分别为交叉率和变异率；pc－max和pm－max为交叉率和变异率最大值；pc－min和pm－min为交叉率和变异率最小值；itmax为设定的最大迭代次数；iter为当前迭代次数；favg为所有染色体适应度的平均值；f′为交叉操作中适应度更高的染色体适应度值；f为变异操作中染色体适应度值。

改进后的计算公式使得优良个体的交叉率和变异率随着进化进程线性变化。 当迭代次数增加时，交叉率逐渐降低以保留优秀解并加速收敛，变异率逐渐增加以跳出局部最优并进行全局搜索。这种进化策略能够加速收敛，利于发现优秀解，提高求解效率和质量。 同时，算法使适应度较低的个体始终拥有较高的交叉率和较低的变异率，以促进全局搜索和局部搜索。 改进的公式能够更有效地控制进化过程，提升优化性能。 图6 为每代第一个选中的染色体交叉率和变异率随迭代次数的变化情况。

图6 交叉率和变异率的变化曲线Fig.6 Curve of crossover rate and variability rate

2.3 AGEP-DNN 算法

DNN 中隐藏层层数和隐藏层节点数的设置决定了神经网络的拟合、预测能力与复杂度。 为提高DNN 的精度，同时缩短网络结构参数寻优时间，本文使用AGEP 进行网络结构参数调优。

AGEP-DNN 算法将体现神经网络结构的隐藏层层数和各隐藏层节点数编码到染色体中，当染色体解码时，可将各基因编译成实数，对应于网络结构超参数的值。 本文设置第1 个基因用于表示隐藏层数量L，其余基因用于表示各隐藏层节点数Kl，AGEP-DNN 算法流程如图7 所示。

图7 AGEP-DNN 算法流程图Fig.7 Flow chart of AGEP-DNN network

3 算法验证实验

3.1 数据集的建立

聚能炸药水下爆炸仿真实验中设置不同装药结构和爆距:l/d分别取为0.75、1、1.25、1.5、2；h/d分别取为0、0.312 5、0.625、1.25、1.875、2.5、3.75；r/d分别取为0.562 5、0.75、1.25、1.875、2.5、3.75。 共组成180 组相对比冲量数据，部分原始数据如表2 所示，训练集和测试集的比例为8∶2。 为解决各变量间数量级相差过大的问题，对数据进行归一化处理，提高相对比冲量数值的预测精度。

表2 部分原始数据Table 2 Partial original data

3.2 实验环境与评价指标

实验环境:CPU 型号为AMDRyzen7 5800H，主频3.2 GHz；GPU 型号为NVIDAGeForceRTX 3050。 算法基于Python 语言实现，使用软件Jupyter Notebook 运行程序。

算法及对比算法的评价指标分别为RMSE、平均绝对误差(MAE)、均方误差(MSE)和平均绝对百分比误差(MAPE)。 四种指标计算方法分别如式(2)及式(6) ~(8)所示。

3.3 实验及结果分析

为验证AGEP-DNN 比冲量预测模型的有效性，选用BP 神经网络、CNN、循环神经网络和DNN 四类对比算法，包含BP 神经网络、遗传算法(GA)优化BP 神经网络(GA-BP)、人工蜂群(ABC)优化BP 神经网络(ABC-BP)、粒子群(PSO)优化BP 神经网络(PSO-BP)、CNN、长短期记忆网络(LSTM)、 DNN、GEP 优化DNN(GEP-DNN)和AGEP 优化DNN(AGEP-DNN)共9 种算法进行实验对比，在保证参数及初始条件一致的前提下，验证AGEP-DNN 在比冲量预测方面的可行性。 GEP 和AGEP 初始参数设置如表3所示，BP、DNN、GEP-DNN 和AGEP-DNN 4 种网络的参数设置如表4 所示。

表3 GEP 和AGEP 初始参数Table 3 GEP and AGEP initial parameters

表4 神经网络参数设置Table 4 Neural network parameters settings

9 种智能模型的比冲量预测结果如表5 所示。与BP 神经网络相比较，根据经验设置的DNN 模型获得的MAE、MSE、RMSE、MAPE 分别提高了86.33%、83.64%、76.96%、67.06%，说明DNN神经网络能够解决浅层神经网络对水下爆炸过程中的复杂非线性关系处理能力不足的问题。 与DNN 相比，GEP-DNN 模型获得的MAE、MSE、RMSE、MAPE 分别提升了28.97%、56.16%、33.79%、30.25%，表明GEP 通过对网络的拓扑结构进行进化搜索，获得了更优的网络结构。 与GEP-DNN 相比，AGEP-DNN 模型的MAE、MSE、RMSE、MAPE 分别提升了15.31%、 0.87%、0.44%、24.39%，验证了调整遗传操作交叉率和变异率的有效性。

表5 9 种智能模型比冲量预测结果对比Table 5 Comparison of nine intelligent models for predicting specific impulse

9 种预测模型在包含25 组样本的测试集中得到的预测值与真实值偏差如图8 所示，可见，本文算法的预测值在各样本中均最接近真实值。

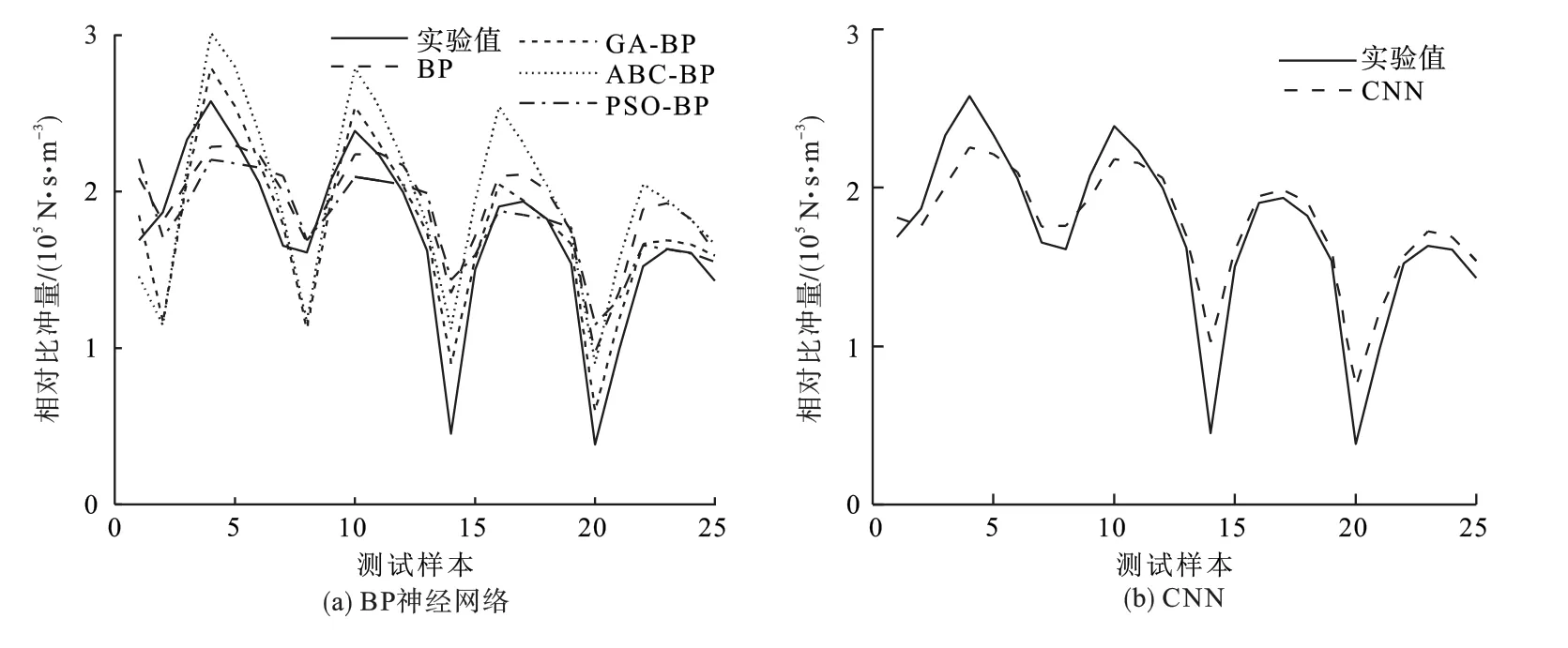
图8 对比算法预测结果Fig.8 Prediction results of comparative algorithms

图9 反映了AGEP-DNN 与GEP-DNN 种群适应度(RMSE)的变化过程。 可见，与GEP-DNN相比，AGEP-DNN 的适应度曲线后期收敛速度更快，说明自适应遗传算法可更好地完成寻优任务。

图9 AGEP-DNN 与GEP-DNN 的RMSE 比较Fig.9 Comparison of RMSE between AGEP-DNN and GEP-DNN

4 结论

本文基于AUTODYN 的数值仿真数据，建立了水下聚能装药比冲量预测模型(AGEP-DNN)。利用DNN 挖掘了装药药柱长径比、相对轴向距离、相对径向距离和比冲量之间的复杂非线性关系，采用AGEP 算法优化了DNN 的结构参数，提升了网络的预测效果。 在包含9 种智能算法的仿真实验中， AGEP-DNN 模型在 MAE、 MSE、RMSE、MAPE 四个精度评价指标中均具有最小值，验证了模型的有效性。

AGEP-DNN 水下聚能装药比冲量预测模型的构建为确定聚能战斗部装药载荷分布规律提供了算法和理论依据，有助于评估聚能战斗部在水下环境中的毁伤效应，可用于军事和爆炸物研究领域。