连续性电液伺服系统位移轨迹的滑模跟踪控制

2024-03-11王峻程武俊峰祝永涛

黑龙江科技大学学报 2024年1期

郑爽, 王峻程, 武俊峰, 祝永涛

(1.黑龙江科技大学电气与控制工程学院, 哈尔滨 150022; 2.黑龙江龙煤双鸭山矿业有限责任公司, 黑龙江双鸭山 155199)

0 引言

阀控液压缸系统是液压控制系统中应用较为广泛的一个分支,其被大量应用于国防、航天等领域[1-2]。由于液压系统中存在液体流动,液压阀阀口的流量系数存在一个非线性关系[3]。

液压伺服系统是通过油流量的流动产生压强来带动液压阀运动,从而推动活塞杆位移。在液压阀运动的过程中,往往将输入电信号与位移信号视为线性关系。阀芯在零位附近动作时便会面临着正负间跳动的问题,阀芯的负载压力增益也将不连续,导致整个系统在阀芯零位附近运动时产生抖振问题[4-6]。另外,液压阀阀芯运动时,阀芯凸肩会与阀口之间产生间隙,导致通流截面积发生改变,液压油的流态也会随之从层流状态改变为湍流状态[7]。也就是说,阀芯在零位附近运动时,电信号与位移信号并不是呈线性关系[8],由于液压缸自身的泄漏及油流特性,导致液压缸在零位附近的压力增益有一定的缓冲。

针对电液伺服系统在阀芯零位附近运动时产生的抖振问题,笔者根据液压缸实际工作情况,采用双曲正切函数拟合电液伺服系统的压力灵敏度,根据液压阀在零位附近工作时进行泰勒展开,确定双曲正切函数的参量和连续性电液伺服系统方程,结合滑模控制方法,设计符合实际功率的控制器,以提高活塞杆位移跟踪精度。

1 连续性电液伺服系统的改进

1.1 电液伺服系统

电液伺服系统原理,如图1所示。由上部液压缸和下部液压阀组合而成。

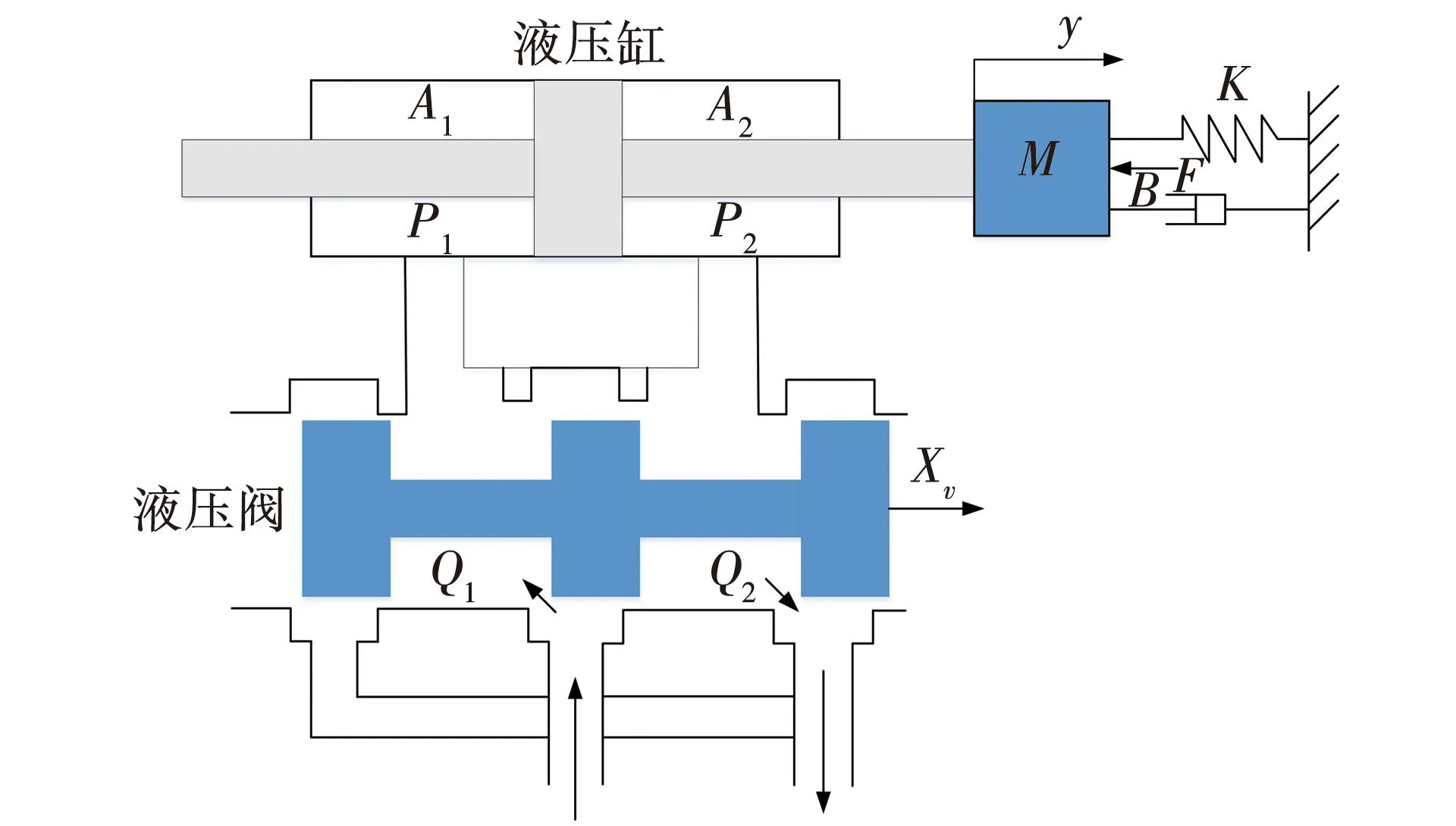
图1 电液伺服系统原理Fig. 1 Schematic of electro-hydraulic servo system

图中,M为等效总质量;B为黏性阻尼系数;K为负载的弹簧刚度;F为作用于活塞杆的任意外负载力;y活塞杆位移值;xv为阀芯位移值;A1为进油腔容积;A2为出油腔容积;P1、P2为液压缸两腔压力;Q1、Q2为液压缸两腔流量。

1.2 传统伺服阀流量方程

电液控制系统的各部分均在同一大气压下,不同的控制电流信号驱动液压阀阀芯运动时,伺服阀流量方程为

(1)

式中:QS——负载流量;

Cd——流量系数;

w——节流口面积梯度;

kx——伺服阀增益;

u——控制输入;

Pg——供油压力;

Ps——负载压力。

式(1)描述了典型的四通滑阀的流量与控制输入之间的关系,这是目前被普遍认可的流量公式。

1.3 连续性伺服阀流量方程

在式(1)伺服阀流量方程中,采用符号定义来拟定液压阀负载压力的压力增益函数。其中符号函数为

(2)

由式(2)可知,其表达的是阶跃函数,根据不同的应用场景,以及所需的不同的精度要求,对符号函数的导数,将使用近似方法或进行特殊处理来描述其变化。针对这个问题,笔者发现液压阀在零位附近动作时,由于制造工艺的缺陷和油流自身特性,使压力增益不是单纯的线性关系。根据电液伺服系统的实际工作情况进行函数拟合,可以得到更加贴合实际的压力增益函数为

ks=tan h(λxv)。

(3)

由双曲正切函数的斜切率代表的负载压强差公式为

(4)

电液伺服控制系统中,通常把阀芯位移与控制输入量近似视为比例环节

xv=kxu。

(5)

将式(3)替换式(2)代入到式(1)中,结合式(5),伺服阀流量方程最终为

(6)

对比式(1)与式(6)可以看出,伺服流量方程中的不连续符号已经被替换成双曲正切函数代表的连续性伺服流量方程。但是对于双曲正切函数中的λ值需要进一步验证,因此先设定电液伺服系统不处于零位状态时,推导伺服阀的三个系数来求解λ值,流量增益可表示为

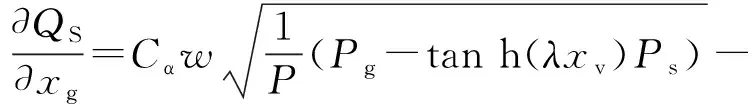
(7)

流量压力系数可表示为

(8)

伺服液压阀压力增益可表示为

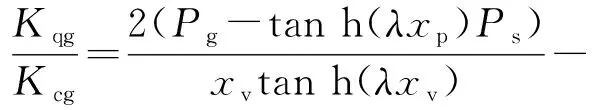
(9)

式(7)～(9)是电液伺服系统在非零位附近状态下的液压阀3个系数表达式[9-10]。若不考虑液压阀小开口时液体流态的非线性变化,则可以得到伺服阀在零位附近的3个系数为

(10)

结合式(3)和式(10)在电液伺服系统工作在零位附近进行泰勒展开式,将工作点标记为A,可以得:

(11)

联立式(3)、(10)和(11)可得,λ的近似表达式为

(12)

不同的λ值所对应的压力增益函数如图2所示。当λ值接近于无穷大时,液压阀的压力增益才会与符号函数相似,由式(12)可知,当电液伺服系统的其他参数固定时,λ将是一个常数。

图2 零位附近压力增益Fig. 2 Pressure gain near zero

由式(12)可知,当λ的值确定时,电液伺服系统在零位附近的压力灵敏度只与液压阀的位移相关。由图2可以看出,当λ的值不为无穷大时,压力增益即使在零位附近依旧连续。因此连续性电液伺服系统的伺服阀流量方程可以改写为

(13)

1.4 液压缸受力平衡方程

液压缸中活塞杆做往复运动时的流量方程可以表示为

(14)

式中:As——活塞有效面积;

V——两容腔总面积;

βe——有效体积弹性模量;

y——活塞杆位移。

对液压缸进行整体受力分析,并运用牛顿第二定律将活塞杆运动时的平衡方程为

(15)

式中:m——等效总质量;

K——负载的弹簧刚度。

联合式(14)、(15)可以表示为

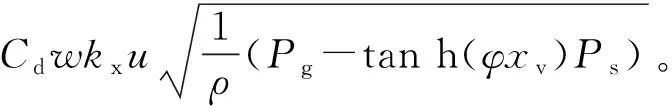
(16)

由式(16)可以得,Ps负载压力表达式为

(17)

根据伺服阀流量方程、液压缸流量连续性方程和液压缸平衡方程,即联立式(13)～(17)可以得:

(18)

2 滑模控制器设计

电液伺服系统为非线性数学模型,当系统中的参量发生改变时,将极大地影响活塞杆位移跟踪效果[11-12]。针对这个问题,提出了滑模控制策略来保证系统受到外界干扰或者系统参量发生改变时,活塞杆位移跟踪效果良好。

为确保活塞杆位移跟踪效果,将活塞杆实际位移与期望轨迹进行对比,得到电液伺服系统位移跟踪的误差值为

e=x1d-x1。

(19)

由式(19)可以将伺服液压系统视为三阶系统,滑模面可以设计为

(20)

为了使其他曲线快速靠近S面,则需要设计滑模控制的趋近律。选用指数形式的趋近律,其表达式为

(21)

将式(19)代入到式(20)可得:

(22)

联合式(21)、(22)可解得:

(23)

由式(23)解得,控制器的表达式为

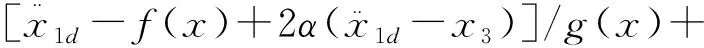
(24)

3 仿真结果与分析

在Matlab环境下,采用脚本形式对液压伺服系统进行编写,其中,包括系统的变量、输入环节、控制环节和输出环节。通过Simulink对整个系统进行搭建并调用系统脚本文件,通过示波器模块观测期望轨迹、实际轨迹及控制器波形。整体系统模型搭建如图3所示。

通过修改控制器脚本文件,将传统伺服液压系统与连续型伺服液压系统进行比较,对比在同一期望轨迹下,两者产生的位移跟踪效果,仿真结果如图4所示。

图3 伺服液压系统模型Fig. 3 Servo hydraulic system model

由图4可以看出,不论是传统系统还是连续性系统,都能在极短的时间内完成轨迹跟踪。这说明连续性系统与传统的系统具有统一性,也验证了连续性系统模型的正确性。

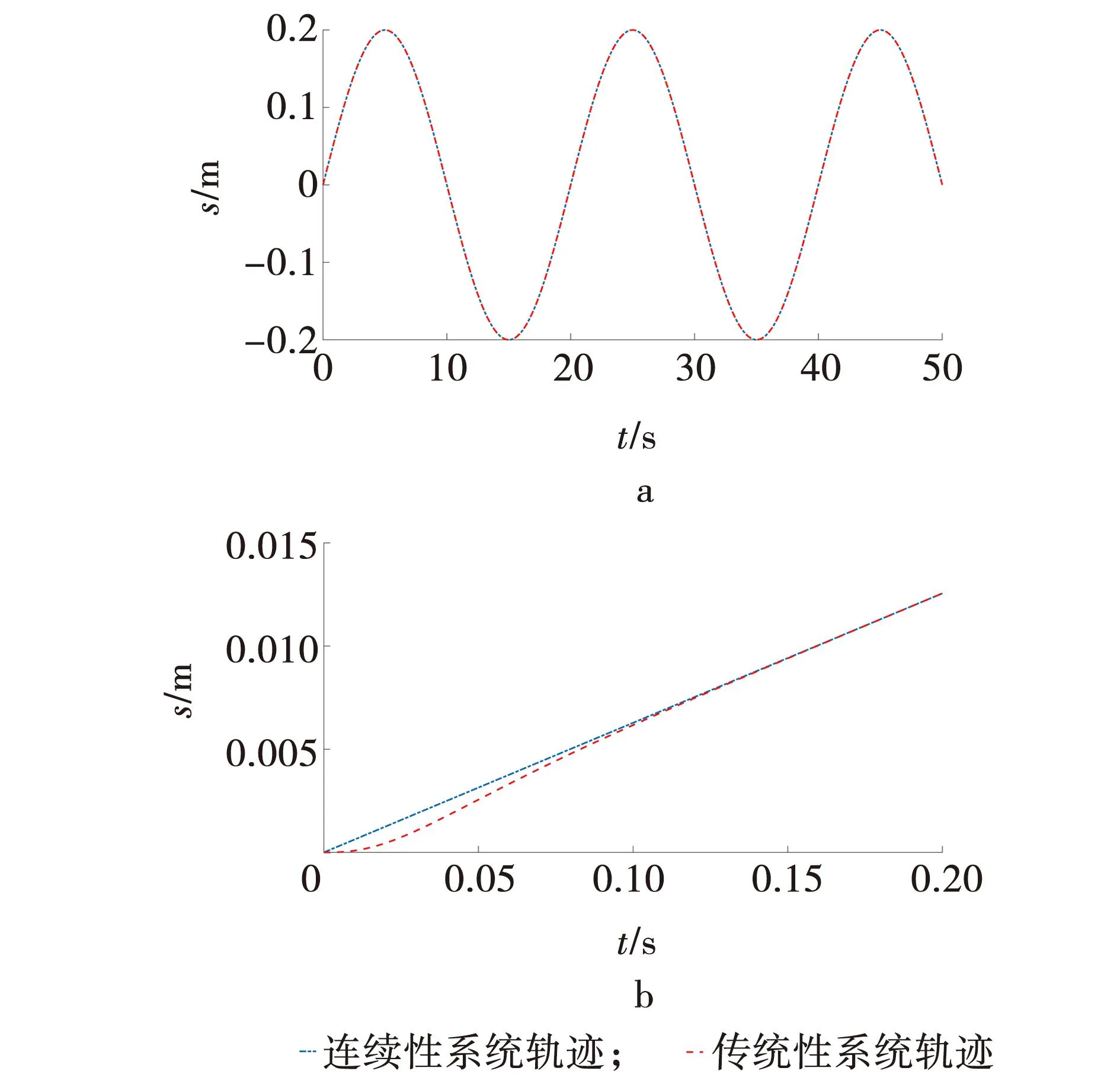
图4 位移跟踪轨迹Fig. 4 Displacement tracking trajectory

两套系统的差异性应该表现在系统的抖振问题上,因此对系统的输出信号进行观测,结果如图5所示。由图5可见,传统的控制器输出波形,由于期望轨迹是周期为20 s的正弦函数,那么控制器输出波形也类似于周期为20 s的正弦函数。这也验证了前文所描述的控制信号与位移信号成比例的推论。

为了验证系统的抖振问题,放大控制器在10 s左右的输出波形。控制器输出波形不再是一条平滑的曲线,而是一段频率高达2 kHz的锯齿波。也正是高频的锯齿波信号对活塞杆位移进行高频的调节,才使系统位移轨迹跟踪良好。

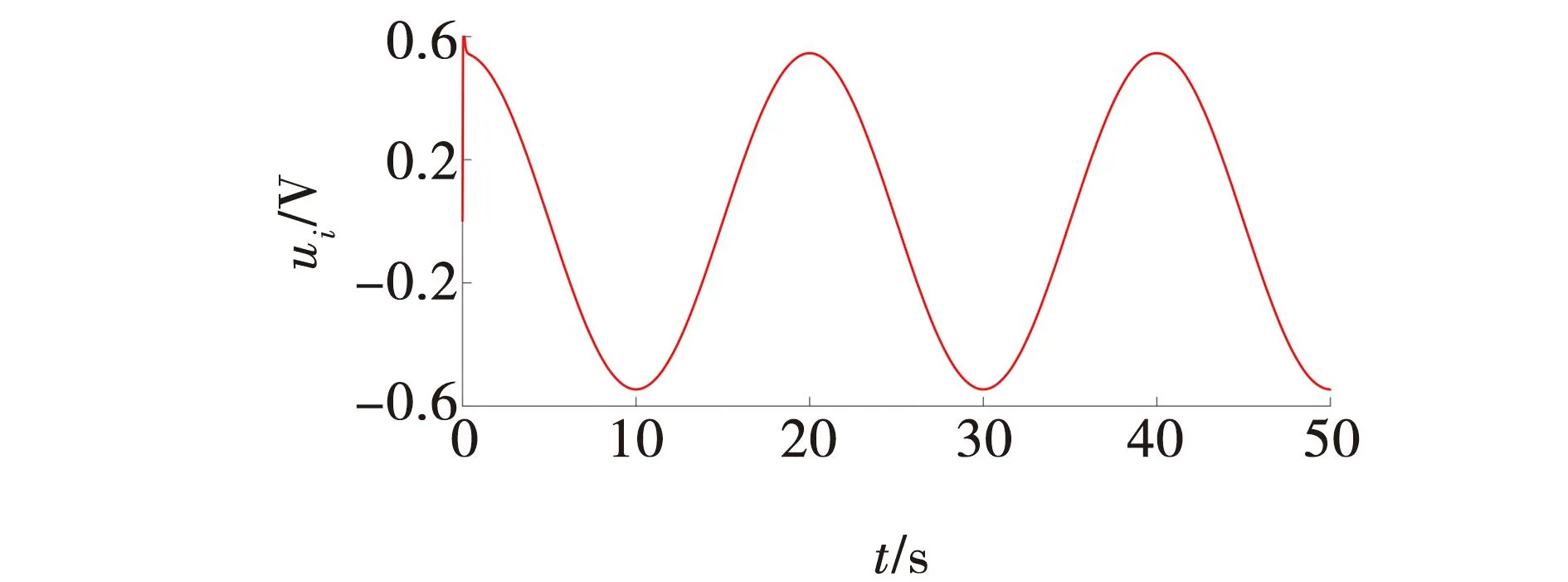
图5 控制器输出波形Fig. 5 Controller output waveform

实际中,控制器输入信号很难达到2 kHz频率以上的信号调节,往往是输入信号还未达到最高点便开始递减,导致控制信号的失真,也是系统产生位移偏差的主要原因。为贴合实际情况下的控制器输出能力,对控制器模块的脚本文件进行修改,限制控制器输出波形的调节频率,再观测系统的位移跟踪效果,结果如图6所示。

图6 控制器输出范围内的位移追踪Fig. 6 Displacement tracking in controller output range

对比图5与6可以发现,当控制器输出能力达不到高频调节时,活塞杆的位移跟踪将产生漂移,得系统的控制精度达不到理想的需求。因此为消除控制器高频调节的问题,采用双曲正切函数替换传统伺服液压系统的符号函数,使伺服液压系统即使在零位附近依旧连续可微。连续弄液压阀系统与传统液压阀系统的控制器输出波形对比,如图7所示。

由图7可以看出,两种系统的控制器输出波形大致重合,可见控制活塞杆做正弦运动时,两套系统的输出能力一致。但是若观测20 s附近的控制器输出波形可以看出,相对于传统液压阀系统,连续型液压阀系统解决了系统中存在的抖动问题,使液压阀系统的控制器输出波形更加平滑。

图7 连续型液压阀对比传统液压阀控制器输出Fig. 7 Continuous hydraulic valve compared with traditional hydraulic valve controller output

连续型液压阀系统的优越性也体现在控制策略上,两种系统的滑模面趋近轨迹如图8所示。滑模控制主要是根据系统所期望的动态特性来设计系统的切换滑模面,通过滑动模态控制器使系统从滑模面之外向切换滑模面收缩。

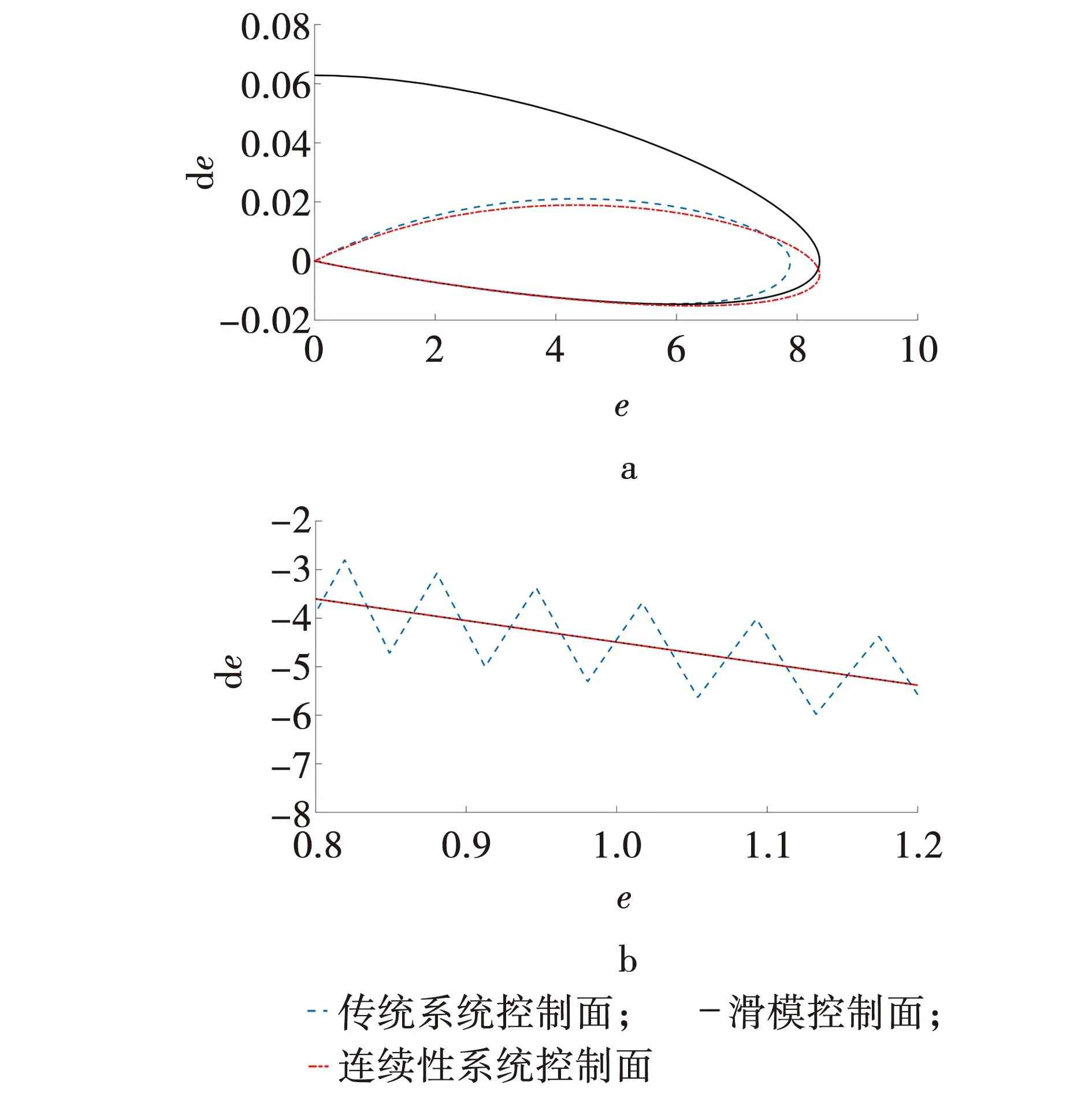
图8 两者系统的滑模面趋近轨迹Fig. 8 Approaching trajectories of sliding mode surface of two systems

两种系统都从滑模面之外向着切换滑模面逼近,当系统到达切换滑模面时,都能沿着切换滑模面到达系统原点。但是对比两种系统的控制面可以看出,连续性系统的控制面比传统系统的控制面更快与滑模控制面重合,并且连续性系统的控制面不会穿越滑模控制面,连续性系统的控制面相比于传统系统控制面更加接近于理想滑模面轨迹,也进一步说明连续性系统比传统系统具备更加良好的动态特性。