桥梁预拱度对行车舒适性的影响及桥面线形调整
2024-03-09郑元勋王博立王长柱
郑元勋, 孔 孟, 王博立, 王长柱, 陈 静
(1.郑州大学 黄河实验室,河南 郑州 450001;2.郑州大学 水利与交通学院,河南 郑州 450001;3.中交第三公路工程局有限公司,北京 100304;4.中国建筑第七工程局有限公司,河南 郑州 450004)
随着中国经济的发展,行车舒适性问题也逐渐受到了广泛的关注。在大跨连续刚构桥中,通常设置成桥预拱度来抵消运营期间混凝土收缩徐变以及活载作用导致的跨中下挠,然而预拱度的设置也会形成以跨径为波长的特定波浪形桥面线形。这种桥面线形将对桥上高速行驶的车辆产生周期性的波形扰动,它不仅影响乘客乘车体验,同时还影响乘客的身心健康[1]。
目前,针对桥梁预拱度对行车舒适性的影响,现有研究中主要围绕简支梁的预拱度进行。如曹胜语等[2]以行车舒适度为评价指标,分析不同跨径下的简支梁满足行车舒适性要求的最大上拱度值。钟明全等[3]分析PC板梁徐变上拱对车辆振动响应和行车舒适度的影响,提出了基于公路设计行车速度的徐变上拱度控制值。马春佳[4]研究了预应力混凝土空心板梁桥徐变上拱与行车舒适性之间的关系,探索性地建立了行车舒适性指标和桥梁上拱度之间的数学关系式。在车-桥耦合振动方面,周小烨[5]、王旭军等[6]对简支梁的上拱度对于行车舒适性的影响进行研究,得出了桥梁振动相对于上拱度对车辆振动影响很小的结论。此外,刘世忠等[7]、Deng等[8]、李武生等[9]用数值方法模拟了车辆与桥梁的动力响应,表明桥面不平度是车-桥耦合振动的主要激励源。对于连续刚构桥来说,其预拱度取值明显大于简支梁,且预拱度作为桥面不平度的重要组成部分,因此有必要对预拱度对行车舒适性的影响做出进一步研究。
本文采用MATLAB/Simlink建立1/4车辆模型,将基于滤波白噪声生成的路面时域模型与按照余弦曲线分配法设置的成桥预拱度叠加生成的桥面不平度作为输入荷载。根据不同跨度下的成桥预拱度对于车辆竖向的激振效果,得出桥梁的预拱度值、车速、跨径对于桥面行车舒适性的影响。最后,根据仿真结果提出改善桥面行车舒适性的具体措施。
1 基于滤波白噪声法的桥面时域模型
1.1 桥面激励模型
桥面不平度是汽车振动的主要振源,它使汽车在行驶过程中产生行驶阻力以及振动。当桥面等级和行车速度一定时,桥面不平顺的速度功率谱密度可以认为是白噪声响应的功率谱密度。
(1)基于功率密度谱的频域描述。桥面不平度可以近似处理为平稳的、各态经历的随机过程。其中功率谱密度的拟合表达式为
(1)
式中:Gq(n0)为路面不平度系数,m3;n为空间频率,m-1;n0为参考空间频率,n0=0.1 m-1。
(2)基于滤波白噪声的桥面时域描述。一阶滤波白噪声系统是指激励为白噪声的一阶单自由度线形系统,一阶滤波白噪声系统的频响函数为[10]
(2)
式中:ω为圆频率,rad/s,ω=2πun;u为汽车行驶速度,m/s;n1为路面空间截止频率,n1=0.01 m-1。
将式(2)转换为微分表达式,故最终基于滤波白噪声法桥面随机激励的时域描述为

(3)
1.2 成桥预拱度线形设置
目前设置成桥预拱度的方法一般都是在理论计算的基础上,根据经验确定跨中最大预拱度后,按某种曲线向全跨分配。由于余弦曲线线形符合连续刚构桥的徐变变形规律,且在跨中以及墩顶处曲线斜率为零。因此现有桥梁线形通常按照余弦曲线进行分配,具体函数如下。
边跨曲线方程:

(4)
中跨曲线方程:
(5)
式中:L为跨径;fcz为中跨跨中成桥预拱度。
1.3 桥面时域模型的建立
根据我国JTG F80/1—2017《公路工程质量检验评定标准》,在新建桥梁的桥面铺装实测项目中,高速公路、一级公路的沥青混凝土面层国际平整度指数最低要求要达到2.5 m/km。国际平整度指数与路面功率谱密度之间存在以下关系[11]:
(6)
式中:a0为系数,a0=103m-1.5;Gq(n0)为路面不平度系数。
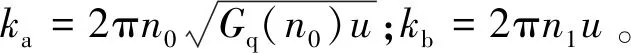
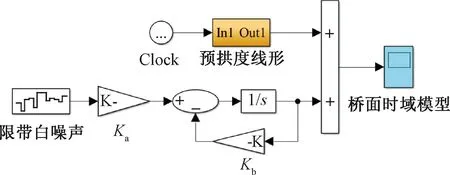
图1 桥面不平度时域仿真模型
为保证当车辆以不同的车速在桥梁的设计线形下行驶时,同样的行车区间内其桥面历程的幅值完全一致,参考文献[12]中的“方法三”来对限带白噪声参数进行设置,具体设置如下:其功率谱密度设置为0.5,同时采样时间设置为(10u)-1,其中车速u的单位为m/s。
2 车辆竖向振动舒适性分析
2.1 车辆-座椅系统模型的建立
在车辆的行驶过程中,桥面的横向坡度并不发生变化,因此主要考虑车辆的垂向振动。如图2所示为3自由度的1/4车辆-座椅模型,由于轮胎阻尼要比悬架阻尼小几个数量级,对车辆的行驶性能影响很小,因此通常忽略轮胎的阻尼[13]。

图2 1/4车辆-座椅模型简图
忽略路面激励引起的质量转移,1/4车辆模型的运动微分方程为
(7)
式中:Z0为桥面激励;Z1为轮胎垂直振动位移;Z2为悬架质量垂直振动位移;Z3为车辆座椅垂直振动位移。以某国产轿车为研究对象,其余结构参数见表1。

表1 车辆结构参数
在Simlink中搭建的1/4车辆仿真模型如图3所示,其中示波器输出车辆振动加速度以及预拱度线形,其中车辆模型根据式(7)进行搭建。

图3 1/4车辆仿真模型
2.2 行车舒适评价指标
在1/4车辆模型中,主要考虑车辆的竖向加速度对于乘客或者驾驶员的影响。本文采取基于国际标准化组织所提出的ISO 2631-1:1997(E)标准[14]的加权加速度均方根值法作为行车舒适性的评价指标。
(1)基本评价方法——加权加速度均方根值RMS[15]:
(8)
式中:T为振动的分析时间,s;aω(t)为瞬时频率加权加速度幅值。
RMS的大小范围与行车舒适性之间的关系如表2所示[14]。

表2 加权加速度均方根值与人体舒适性的关系
(2)辅助评价方法——最大瞬态振动值MTVV。对于特殊路面,相对于RMS,用最大瞬态振动值MTVV能更好地评价振动在短时内对人体的影响,最大瞬态振动值法本质为持续加权加速度均方根值aω(t0):
(9)
MTVV=max[aω(t0)]。
(10)
式中:τ为持续平均积分时间,通常取1 s;t0为选取计算时间。此外,ISO 2631-1:1997(E)标准规定了MMTV和RMS的经验换算公式,同时当两者比值大于1.5时,则采用辅助评价方法替代基本评价方法来评价振动对人体的影响。
在ISO 2631-1:1997(E)规范中,虽然建立了最大瞬时振动冲击指标,但是并未对MTVV进行分级,参考文献[16]中提出的关于路桥过渡段的相关评价方法,其相关舒适性对应评价标准如表3所示。

表3 最大瞬态振动值与人体舒适性的关系
2.3 模型仿真分析
通过查阅资料,选取10座在实际工程中按照余弦曲线分配法设置成桥预拱度的桥梁,如表4所示。对10座主跨跨径为110~200 m的连续刚构桥进行行车舒适性研究,同时为了对比成桥预拱度对行驶车辆的激励效果,设置以下2种工况。
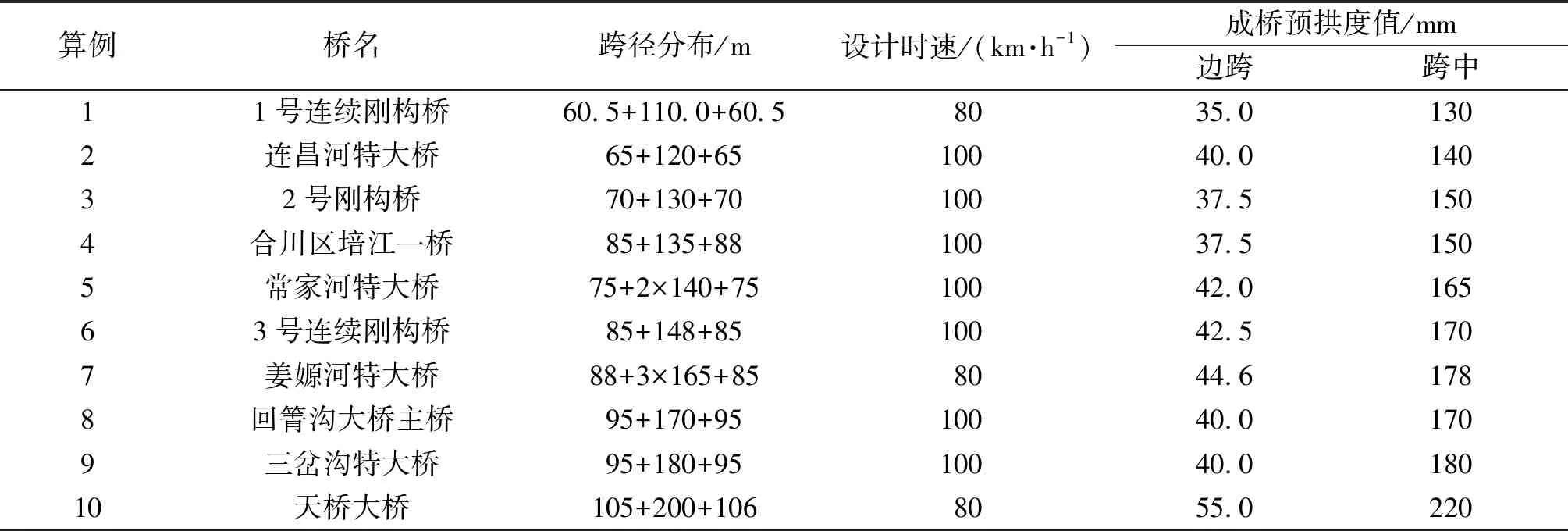
表4 实桥相关参数
(1)工况a:桥梁成桥线形下的桥面激励;
(2)工况b:桥梁设计线形下的桥面激励。
如图4(a)~图4(j)为工况a下的车辆加速度响应及各桥的预拱度线形示意图,图4(k)为工况b下不同的行驶速度所对应的车辆加速度响应,a为加速度,y为成桥预拱度值。

图4 车辆加速度响应及成桥预拱度示意图
表5为边跨、中跨模型仿真结果。如表5所示,由于边跨、中跨线形差异较大,因此分别选取车辆在边跨、中跨行驶时的加权加速度均方根值RMS以及2种工况下的RMS比值作为预拱度影响行车舒适性的衡量指标。

表5 边跨、中跨模型仿真结果
由于车身簧载质量加速度受到车辆行驶速度的影响较大[17],现分析车速在100 km/h时,主跨跨径与桥面加速度响应之间的关系。如图5所示,随着主跨跨径增加,2个工况下的边跨、中跨加速均方根比值明显呈线性正相关,且最终比值趋近于1。说明随着跨径的增加,预拱度对行车舒适性的影响逐渐下降;对同一座桥梁,2种工况下中跨处的加速度均方根比值较边跨更大一些,且拟合曲线在边跨处的斜率更大,说明边跨处的行车响应更为明显。

图5 跨径和RMSb/RMSa响应关系
根据表5数据,从全桥加速度响应结果来看,当车辆以设计时速通过桥面时,人体加速度均方根值小于0.315 m/s2,此时人体感受处于舒适范围内。但该评价指标不能反映桥面局部范围的行车响应效果。如图4所示,当车辆以100 km/h驶过桥面时,在边跨3L/8附近存在瞬时加速度峰值大于0.6 m/s2的情况,此时人体在短时内可能会产生不舒适感。现以最大瞬态振动值MTVV为指标,研究边跨处车辆行驶速度对行车舒适性的影响。
表6为工况a下边跨3L/8处MTVV值。如表6所示,当边中跨比在接近于0.55时,随着主跨跨径的增大,其最大瞬态振动值呈逐渐降低的趋势。当车辆行驶速度为100 km/h时,边跨3L/8范围内MTVV与RMS比值大于 1.5。根据表3中的MTVV分级评价范围,此时人体舒适性感受为稍不舒适,因此有必要采取措施对边跨的桥梁线形进行调整从而改善边跨处的行车舒适性。
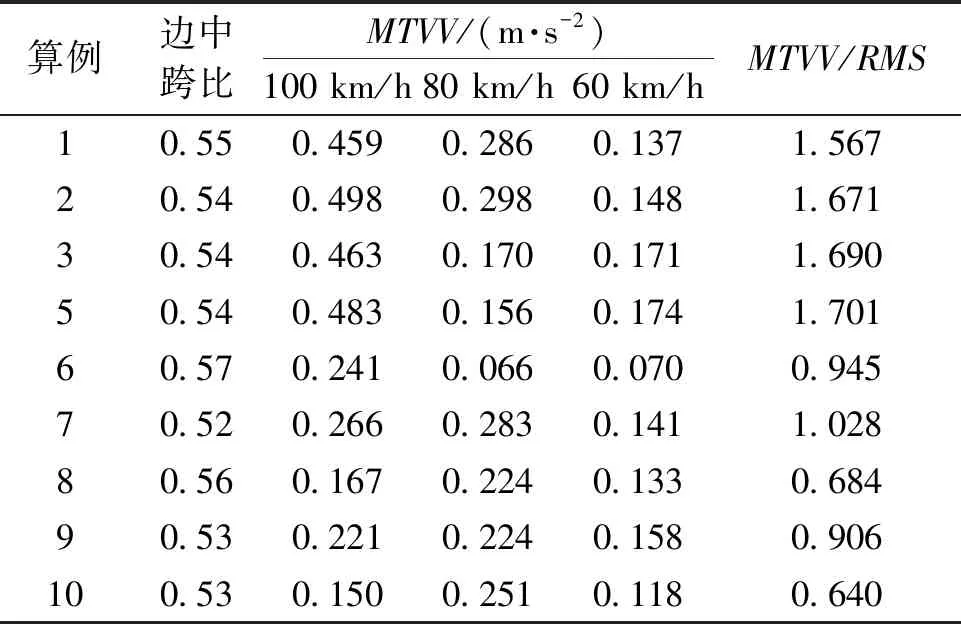
表6 边跨3L/8处MTVV值
3 基于桥面铺装层的桥面线形调整
随着现有桥梁跨径的不断增加,同时在施工阶段受到多种因素的干扰,现有连续刚构桥最终的成桥线形与预期状态之间存在一定误差。目前,连续刚构桥的桥面铺装主要由混凝土调平层和上层沥青铺装组成。因此,针对合龙后的桥面实测线形进行拟合优化,或者在规范允许的范围内对铺装层厚度进行小范围调整,能够进一步提高桥面线形的平顺性。桥面铺装层线形拟合基本原理如下:
g(x)=n·y′(x)+d。
(11)
式中:g为最终的铺装线形;n为成桥预拱度调整系数,当合龙后的桥面实测线形与理想成桥线形完全吻合时其值为1;y′为按照余弦曲线分配法计算的成桥预拱度;d为混凝土调平层厚度,通常取8~12 cm。
线形调整原理如图6所示。方法一:在桥面实测线形的拟合优化中以降低边跨、中跨跨中处的桥面预抛高为目标,从而增加桥面线形的平顺性;方法二:通过增加边墩墩顶混凝土调平层厚度来提高桥面线形的平顺性。
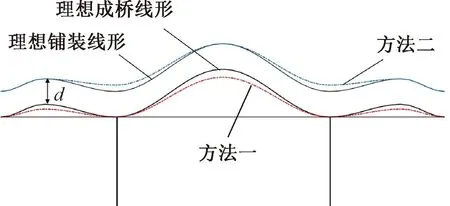
图6 桥面线形调整示意图
参考JTG F80/1—2017《公路工程质量检验评定标准》[18]中对于桥面高程以及桥面铺装的具体要求,如表7所示,方法一、方法二应分别将桥面高程、铺装层厚度控制在检验标准允许偏差以内。同时根据相关研究[19],当铺装层混凝土材料与桥面板结合良好时,铺装垫层厚度的增加对铺装材料内部应力的分布几乎没有什么影响。

表7 桥面线形调整参考指标
以某连续刚构桥为例,该桥跨径分布为65 m+6×120 m+65 m,其桥面混凝土调平层设计厚度为8 cm。在铺装层施工前需要对桥面线形进一步拟合,以提高桥面的平顺性。以边跨、中跨加速度均方根值和边跨3L/8处的大瞬态振动值为指标,研究方法一、方法二对于改善桥面行车舒适性的效果,得到的加速度响应的评价指标如表8所示。

表8 方法一及方法二综合作用下加速度响应结果
根据表8中的仿真结果,整理结果如图7~8所示,当处于工况7时,边跨3L/8处预抛高与边墩墩顶位置预抛高差值达到最小,边跨与中跨的RMS值如图9所示,某大桥由于在施工过程中因施工工期以及施工工艺上的原因,悬浇箱梁顶面施工完成后表面平整度较差,现在基于上述方法对桥面线形进行调整。调整前后边墩桥面行车舒适性提高了11%,边跨位置行车舒适性提高了16.3%,边跨3L/8处的最大瞬态振动值降低了20.7%。

图7 边跨3L/8处RMS响应结果
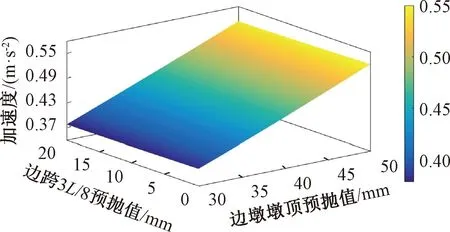
图8 边跨3L/8处MTVV响应结果

图9 边墩桥面线形拟合
变化不太明显,但边跨的RMS值以及边跨3L/8处的MTVV值为最小,此时行车舒适性达到最优。说明通过线形拟合优化降低边跨3L/8处的预抛高值以及增加边墩墩顶混凝土调平层厚度能有效改善边跨桥面的行车舒适性。
综上所述,按照以上方法对桥面线形进行调整,既有效改善了桥面的行车舒适性,也兼顾成桥预拱度在运营期间抵消跨中下挠的作用。
4 结论
本文通过采用滤波白噪声法建立桥面时域模型,同时将得到的桥面时域模型与按照余弦曲线分配的成桥预拱度值进行叠加模拟成桥后的桥面不平度。采用MATLAB/SIMLINK搭建成桥后的桥面不平度模型与1/4车辆模型,并对实桥结构进行仿真分析,得出了以下结论。
(1)以加速度均方根值RMS为评价指标时,边跨、中跨处的RMS值均小于0.315 m/s2,人体感受均处于舒适范围以内;同时随着桥梁跨径的增加,预拱度对行车舒适性的影响逐渐下降,桥面平整度对行车舒适性的影响逐渐增加。
(2)以最大瞬态振动值MTVV为评价指标时,当桥梁跨径较小时,车辆座椅的竖向振动受成桥预拱度值与车辆行驶速度的影响较为明显,在边跨3L/8附近人体会产生稍不舒适感。因此在计算边跨成桥预拱度取值时,应该同时考虑桥梁设计时速的影响。
(3)针对边跨3L/8位置附近产生的行车不舒适感,通过线形拟合降低边跨3L/8处的桥面预抛高或者增加边墩墩顶混凝土调平层厚度能够有效改善行车舒适性。
