基于灰狼算法和极限学习机的风速多步预测
2024-03-09张文煜马可可郭振海邱文智
张文煜, 马可可, 郭振海, 赵 晶, 邱文智
(1.郑州大学 地球科学与技术学院,河南 郑州 450001;2.郑州大学 计算机与人工智能学院,河南 郑州 450001;3.中国科学院大气物理研究所 大气科学和地球流体力学数值模拟国家重点实验室,北京 100029)
风能作为一种清洁的可再生能源,开发潜力巨大。近年来,中国风电装机总容量迅速增加,但由于风具有间歇性和波动性[1-3],当大规模风电接入电网时,将给电网调度带来困难,解决这一问题的有效方式之一是对未来风速变化的准确预测。随着人工智能的发展,人工神经网络(artificial neural networks,ANN)因具有强大的非线性数据拟合能力在风速时间序列的建模和预测中颇具优势[4]。
已有研究大多是对风速进行一步或少数几步预测,而对于大步长风速预测的研究还处于初级阶段,特别是用于风电场的4 h、16步预测[5]。Liu等[6]使用一种基于谱聚类和回声状态网络的方法预测未来16步风速。Zhao等[7]建立了16个一维卷积神经网络来预测未来16步风速,提供了16步风速预测的一种可行思路,但计算开销较大。
鉴于此,本文使用极限学习机(extreme learning machine,ELM)[8]作为风速时间序列的预测模型,并使用多输入-多输出策略建立ELM。ELM是一种特殊的单隐层前馈神经网络,与传统的前馈网络使用梯度下降和误差反向传播进行网络更新的方式不同,ELM随机地生成隐含层的权值和偏置并解析地计算隐含层到输出层的权值参数。因此,ELM具有计算速度快、泛化性能强等优点,适用于风速预测问题[9]。一些研究表明,使用人工智能优化算法求解最优隐含层参数可以降低ELM的输出误差[10]。Mirjalili等[11]的研究结果显示,与粒子群优化、遗传算法等经典的启发式算法相比,灰狼优化(grey wolf optimization, GWO)算法[12]在求解单峰和多峰函数问题时都更具优势。因此,本文采用GWO算法搜索ELM隐含层参数的最优值,并进一步计算输出层权值。
另一方面,风速序列本身具有复杂的非线性特征,单一模型很难取得满意的预测结果。使用信号分解方法将原始数据序列分解成若干具有不同数据特征的子序列的集合,是改进模型预测结果的有效方法。常用的分解方法有经验模态分解(empirical mode decomposition, EMD)[13]、变分模态分解[14]和奇异谱分析等。其中,EMD是应用最为广泛的方法,它能够根据数据自身的时间尺度特征来识别信号中包含的振动模态,并将复杂的原始信号分解为有限个本征模态函数(intrinsic mode function, IMF)。与小波分解等方法不同,EMD不需要预先设定任何基函数,在处理非平稳及非线性数据时具有优势,但EMD存在模态混叠现象。为了解决模态混叠现象,具有自适应噪声的完全集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)[15]算法在分解过程的每个阶段自适应地加入白噪声,并计算唯一的余量信号,其重构误差极低,而且能够产生更好的模态分离结果。韩宏志等[16]使用CEEMDAN分解原始风速信号,将分解结果作为回声状态网络的输入并建立预测模型。Ren等[17]建立CEEMDAN与ANN的混合风速预测模型,并与EMD-ANN、EEMD-ANN等模型进行比较,结果表明:CEEMDAN-ANN模型具有更高的预测精度。
基于以上分析,本文构建了CEEMDAN-GWO-ELM混合模型,用于风速时间序列的多步预测。使用CEEMDAN算法将原始风速分解为若干具有不同数据特征的子序列的集合,在各子序列上建立GWO优化的ELM模型并进行多步预测,最终的预测结果由各子序列的预测重构生成。将提出的CEEMDAN-GWO-ELM模型应用于实际风电场的4 h风速预测问题,进行了预测步长为16的模拟试验和模型比较试验,用于验证该模型在大步长的风速预测问题中的有效性和适用性。
1 数据预处理与特征选择
1.1 数据预处理
1.1.1 具有自适应噪声的完全集成经验模态分解(CEEMDAN)
CEEMDAN通过在每个分解阶段为唯一的余量信号添加高斯白噪声后再进行EMD分解,其分解过程具有完整性[18],能以较低的计算成本提供原始信号的精确重建和更好的模式频谱分离。定义操作符Mk(·)为通过EMD算法得到的第k个模态分量;vi(t)为符合标准正态分布的高斯白噪声;ε为高斯白噪声的标准差。CEEMDAN的计算过程如下。
步骤1 设s(t)为原始信号,对信号s(t)+ε0vi(t)进行I次试验,通过EMD获取第一个模态分量:
(1)
步骤2 在第1阶段(k=1),计算唯一的残差项:
r1(t)=s(t)-IMF1(t)。
(2)
步骤3 以r1(t)作为新的原始信号,进行I次试验,每次试验使用EMD算法分解新构建的r1(t)+ε1M1(vi(t))信号,计算第2个模态分量:
(3)
步骤4 对其余各阶段即k=2,3,…,K,与步骤2和步骤3的计算过程一致。首先计算第k个残差项rk(t),再计算第k+1个模态分量IMFk+1(t):
rk(t)=rk-1(t)-IMFk(t);
(4)
(5)
步骤5 重复执行步骤4,直至残差项无法满足分解条件。此时原始信号s(t)被分解为
(6)
(7)
式中:K为分解得到的模态个数;R(t)为最终的残差项。
1.1.2 归一化
使用最大最小归一化法将模态分量的值z=[z1,z2,…,zi,…,zn]归一化到[0,1]内,如下式:
(8)
式中:zi′为归一化后的元素值;zmax和zmin分别为模态分量中的最大值和最小值;n为模态分量的序列长度。
1.2 输入数据的特征选择
输入数据的窗口大小影响模型的预测水平,这是因为窗口过大会引入冗余信息,而窗口太小会丢失部分有用的信息[19]。本文使用偏自相关函数(partial autocorrelation function, PACF)[20]确定模型输入数据的窗口大小。

2 灰狼算法优化的极限学习机模型
2.1 极限学习机(ELM)
ELM是一种单隐层前馈神经网络,假设它的隐含层节点数为L,输出层的节点数为m,对于输入样本(xi,yi),i=1,2,…,N,N为样本总数,xi=[xi1,xi2,…,xid]T为d维输入数据,yi=[yi1,yi2,…,yim]T为m维输出数据,ELM隐含层的输出可表示为
(9)
式中:G为隐含层节点的激活函数,通常使用sigmoid函数;wk=[wi1,wi2,…,wid]T为输入节点与隐含层节点间的权值向量;bk为隐含层节点的偏置;βk=[βi1,βi2,…,βim]T是隐含层节点与输出层节点间的权值向量。
令ELM的输出值零误差地逼近给定的N个样本,即
(10)
也就是说,存在βk、wk、bk使得
(11)
式(11)可以简化为
Hβ=Y。
(12)
式中:H为ELM的隐含层输出矩阵;β为隐含层与输出层之间的权值矩阵;Y为ELM的理想输出,分别表示为
(13)
(14)
(15)
ELM的训练过程相当于求解出β矩阵,其解可表示为
(16)
式中:H+为H的摩尔-彭罗斯(Moore-Penrose)广义逆矩阵。
2.2 灰狼优化算法(GWO)
GWO是一种元启发式算法,其灵感来源于灰狼,本质上模仿了灰狼的领导阶层和狩猎机制。GWO将每一匹狼作为一个解,设α为全局最优解,γ和δ为全局第二和第三优解,其余候选解记为ω。ω狼(搜索代理)在α、γ及δ狼的带领下进行搜索和狩猎,主要过程可表示为
D=|C·Xp(e)-X(e)| ;
(17)
A=2ar1-a;
(18)
C=2r2;
(19)
(20)
式中:X和Xp分别为搜索代理和猎物的位置向量;D表示搜索代理与猎物的距离;e为当前迭代次数;A和C为系数向量;r1和r2为[0,1]随机数;E为最大迭代次数;a为收敛因子,在迭代过程中从2线性减小至0。
搜索代理X与α、γ及δ狼的距离确定为
(21)
则搜索代理在下一次迭代的位置由下式更新。
(Xδ(e)-A3Dδ)]。
(22)
2.3 极限学习机的参数优化
本文使用GWO选取使得网络输出误差最小的隐含层权值和偏置,通过搜索最优化的隐含层权值和偏置,进一步改进ELM模型的多步预测结果。基于GWO优化的ELM模型的具体步骤如下。
步骤1 初始化GWO参数。其中,最大迭代次数E=2 000,搜索代理的数量C=5,α、γ、δ狼的适应度值Fα、Fγ、Fδ设置为+∞,使用[0,1]中的随机数初始化每个搜索代理的位置向量X。
步骤2 对于第c个搜索代理(c=1,2,…,C),用其位置向量Xc初始化ELM的隐含层权重和偏置,在训练集上求解隐含层与输出层之间的权值矩阵β。在验证集上,计算该灰狼的适应度函数值Fc:
(23)
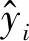
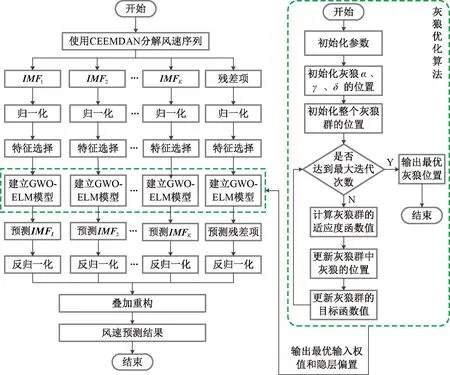
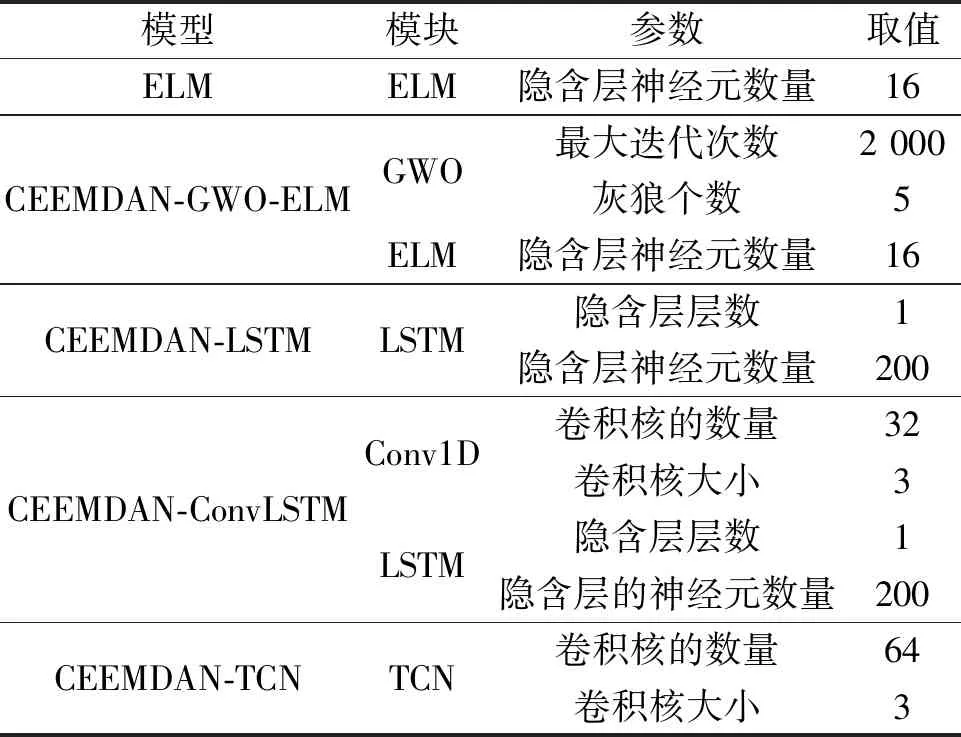
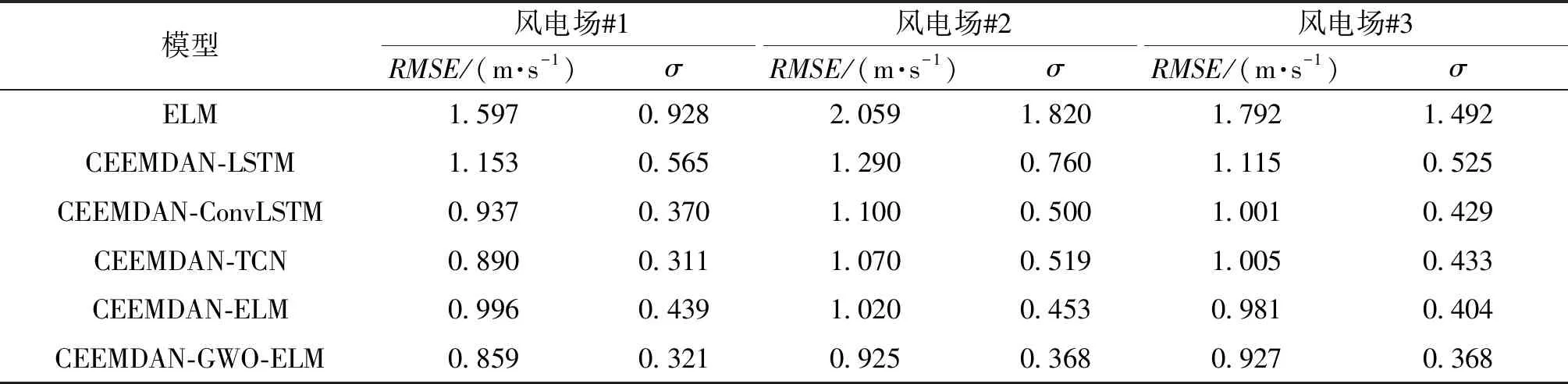
如果该搜索代理的Fc满足Fc 步骤3 对于第c个搜索代理(c=1,2,…,C),使用式(21)和式(22)更新位置向量Xc。 步骤4 重复执行步骤2和步骤3,直到达到最大迭代次数E,输出α狼的位置向量Xα作为ELM的最优隐含层权重和偏置。 本文提出的风速预测模型是由CEEMDAN、GWO及ELM组成的混合模型,记为CEEMDAN-GWO-ELM,图1为混合预测模型流程图。具体步骤如下。 图1 CEEMDAN-GWO-ELM混合预测模型流程图 步骤1 通过CEEMDAN将原始风速序列分解为K个IMF子序列和一个残差项。 步骤2 对分解得到的子序列进行最大最小归一化。 步骤3 计算各子序列在不同滞后阶数下的PACF值,并对模型输入特征进行选择。 步骤4 在每个子序列上,分别建立GWO优化的ELM模型,模型输入由步骤3确定。对未来4 h的风速变化情况进行预测,即16步预测,并对预测结果进行反归一化。 步骤5 对各子序列的预测结果进行重构,得到原始风速序列的混合预测结果。 CEEMDAN将风速序列分解为若干不同频率特征的子序列,以削弱风速序列的非线性[22],从而提高模型的预测水平。由于ELM的隐含层权值和偏置是随机产生的,因此可以使用GWO寻找ELM的最优隐含层权值和偏置,提高ELM预测的精度和稳定性。 本文使用的数据来自中国山东省3个风电场时间间隔为15 min风速观测资料,如图2所示,它们的统计特征如表1所示。对每一个风电场,将原始数据按照7∶2∶1划分为训练集、验证集及测试集,其中训练集用于建立模型,测试集用于模型评价,而在GWO优化ELM参数过程中,将根据ELM在验证集上的适应度值来选择ELM的隐含层参数。 表1 风速序列的统计特征 图2 3个风电场的风速序列 本文使用均方根误差(RMSE)和误差方差σ来评价预测模型的准确性和稳定性。其表达式为 (24) (25) 分别使用3个风电场的数据集建立图1中的预测模型,进行4 h风速预测,即16步预测。 为了验证本文建立的CEEMDAN-GWO-ELM模型的有效性和适用性,选取了4个不同的比较模型。具体地,选取ELM和CEEMDAN-ELM作为CEEMDAN-GWO-ELM的关联模型,用于验证基于CEEMDAN的序列分解方法和基于GWO的参数优化方法对提高ELM模型预测水平的有效性。此外,选择了基于CEEMDAN分解的LSTM[23]、卷积LSTM和时域卷积网络(temporal convolutional network,TCN)[17],分别记为CEEMDAN-LSTM、CEEMDAN-ConvLSTM和CEEMDAN-TCN,用于与CEEMDAN-GWO-ELM的对比分析。上述模型的参数设置如表2所示。 表2 模型的参数设置 以风电场#1为例进行分析。首先使用CEEMDAN对原始风速序列进行分解,得到11个IMFs和一个残差项。其中,残差项的值域约为[-3.553×10-15, 3.553×10-15],其数量级远小于原始序列取值的数量级,对预测结果几乎没有影响,因此,不对该残差项进行建模预测。 计算原风速序列和11个IMFs的偏自相关函数值,选择偏自相关函数值超出95%置信区间的滞后阶数所对应的变量作为输入特征,如表3所示。由表3可以看出,对不同的IMF子序列,模型所选择的输入特征也是不同的。 表3 输入变量选择结果 根据表3中确定的输入特征,在每一个IMF子序列上建立GWO-ELM模型,并对子序列的预测结果进行重构。 图3给出了使用CEEMDAN-GWO-ELM模型在风电场#1的4个仿真案例,左边为未来16步风速的实际值与CEEMDAN-GWO-ELM模型的预测值,右边为每步预测值与实际值的误差。图3中4个仿真案例的预测起始时间分别为2019-04-05T06:00:00、2019-04-05T02:00:00、2019-04-05T22:00:00和2019-04-06T10:00:00。由图3可以看出,该方法能够较好地预测未来4 h的风速变化情况,且随着预测步长的增加,模型的预测偏差始终保持在一定的范围内。这表明本文建立的模型在大步长的风速预测问题中能够产生可靠的预测结果。 图3 CEEMDAN-GWO-ELM预测风电场#1的仿真案例 表4对比了不同模型对3个风电场进行预测的误差指标情况。首先,比较ELM和CEEMDAN-ELM模型的预测结果。可以看出,使用CEEMDAN对原始风速序列进行分解能够显著提高模型的预测水平。具体地,相比于ELM,CEEMDAN-ELM在风电场#1的RMSE下降了37.6%,在其他风电场上的预测精度也有相当大的提升。同时,相比于ELM模型,CEEMDAN-ELM在风电场#1~#3的误差方差分别降低了52.7%、75.1%和72.9%,这表明CEEMDAN分解方法能够在降低模型预测误差的同时提高预测的稳定性。这是因为风速时间序列具有复杂的非线性特征,使用单一模型时通常难以取得满意的预测结果。CEEMDAN将原始风速序列分解为若干具有不同频率特征的子序列,使得预测模型能够更好地描述各数据序列的变化特征,从而提高模型预测水平。 表4 不同模型对3个风电场的预测结果 在对CEEMDAN-GWO-ELM和CEEMDAN-ELM的比较中能够发现,通过搜索ELM的最优隐含层权值和偏置,模型的预测水平得到了进一步提升。结果显示,基于GWO的参数优化使得3个风电场的RMSE分别下降了13.8%、9.3%和5.5%,σ分别下降了26.9%、18.8%和8.9%。这表明与随机初始化ELM隐含层的权值和偏置相比,优化选取的隐含层参数值能够改进ELM的网络性能。本文使用的GWO算法提供了搜索上述最优化参数的有效途径。 进一步分析基于CEEMDAN分解的LSTM、ConvLSTM及TCN在16步风速预测中的表现。表4显示,CEEMDAN-ConvLSTM和CEEMDAN-TCN的预测结果整体上优于CEEMADN-LSTM,这表明在处理风速时间序列的多步预测问题时,卷积网络具有一定的优势,这与文献[5]和[7]的结果一致。与本文提出的模型相比,CEEMDAN-TCN在风电场#1的误差方差略低于CEEMDAN-GWO-ELM,表现出更强的稳定性。除此之外,本文提出的CEEMDAN-GWO-ELM模型对3个风电场的全部评价指标均优于所有的比较模型,表明该混合模型在风速时间序列的多步预测问题中具有较强的适用性。 使用统计模型进行多步预测时,随着预测步长的增加,模型的预测精度和稳定性通常会逐渐下降。这是因为统计模型是基于历史数据集的内在统计规律建立的,并对未来变化进行预估。在多步预测过程中,模型所产生的预测值与真实值之间的偏差会随预测步长的增加不断累积,导致预测误差逐渐增大甚至发散。分析误差随预测步长的变化情况,对讨论多步预测模型在实际应用中的有效性和适用性是颇具意义的。图4直观展示了不同预测模型对3个风电场的RMSE和σ随预测步长的变化情况。 图4 不同模型在3个风电场的误差指标随着预测步长的变化趋势 整体来看,在3个风电场中,所有模型的RMSE和σ都随着预测步长的增加而逐渐增大。以RMSE为例,在风电场#1的预测结果中,各模型的RMSE误差曲线较为集中,且CEEMDAN-TCN和CEEMDAN-GWO-ELM的σ更小。特别地,在预测步长大于12步的情况下(即大于3 h的预测),本文提出的CEEMDAN-GWO-ELM模型在RMSE和σ的比较中都更具优势。在风电场#2和#3的预测结果中,各模型之间具有明显差异。例如在风电场#2中,CEEMDAN-GWO-ELM对未来第4 h风速预测的RMSE和σ分别为1.116 4和0.470 7,分别比排名第二的CEEMDAN-ELM降低了6.4%和14.1%;而在风电场#3中,CEEMDAN-GWO-ELM对未来第4 h风速预测的RMSE和σ分别为1.073 8和0.371 1,分别比排名第二的CEEMDAN-ELM降低了9.8%和24.2%。从图4(b)~4(f)也可以看出,在大于3 h的预测中,CEEMDAN-GWO-ELM模型几乎在所有的预测步长上都有更低的RMSE和σ。这表明,所提出的CEEMDAN-GWO-ELM模型能够更好地描述风速时间序列的复杂变化特征,能够在大步长的预测问题中产生可靠的结果。 (1)利用CEEMDAN将原始风速序列分解为若干具有不同频率特征的子序列能够降低模型的预测难度。 (2)利用GWO搜索ELM的最优隐含层权值和偏置能够提高ELM的预测精度和稳定性。 (3)在3个风电场进行模型比较实验中,提出的CEEMDAN-GWO-ELM混合模型都具有最高的预测水平,验证了该模型具有一定的适用性。 在本文的研究中,CEEMDAN的分解结果存在高频子序列,一定程度上影响模型的预测精度,因此,下一步将在降低高频子序不规则性的基础上改进预测模型。3 CEEMDAN-GWO-ELM混合预测模型
4 算例分析
4.1 数据集


4.2 模型评价指标
4.3 试验设置
4.4 个例分析
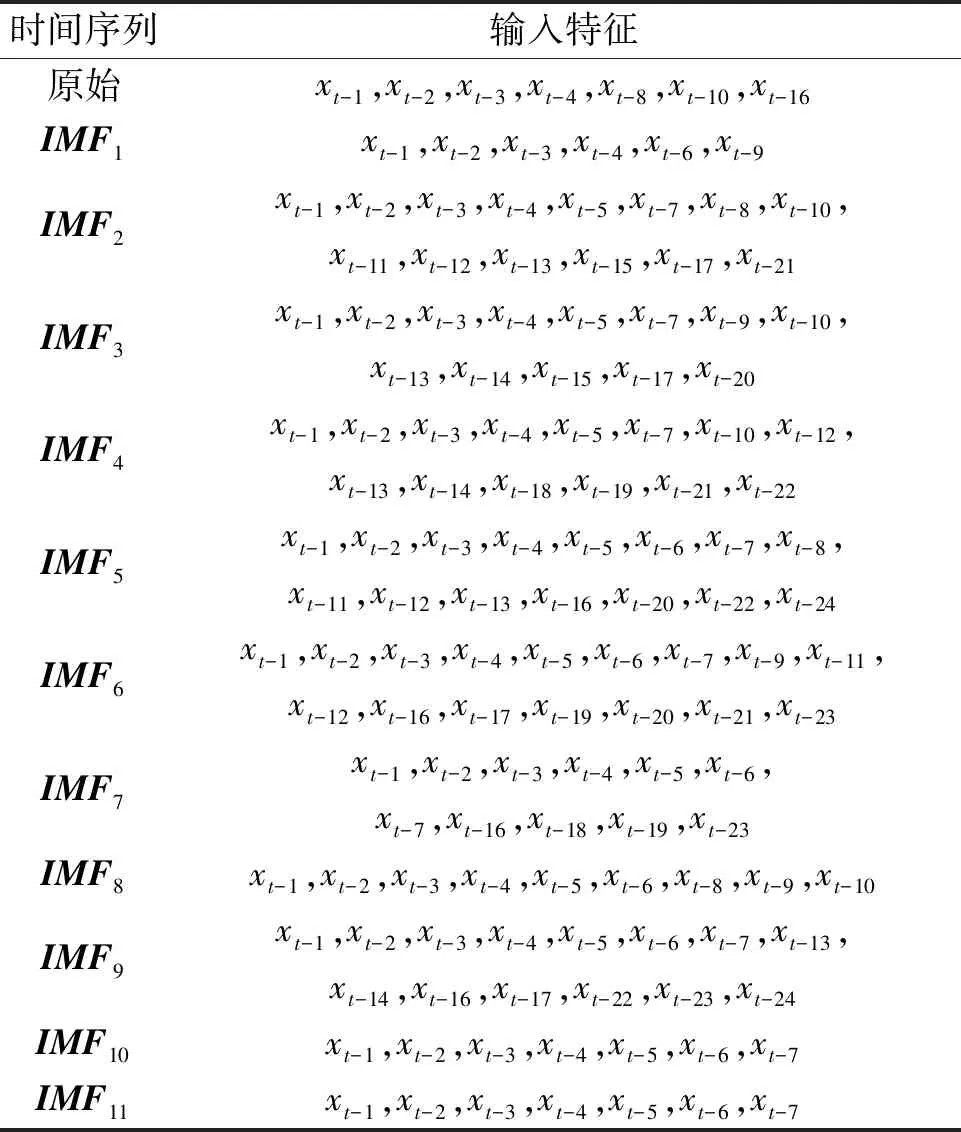

4.5 模型比较分析
4.6 模型的预测性能随预测步长的变化分析

5 结论
