考虑碳排放社会成本的最优峰谷电价研究

左 剑, 孙 傲, 潮 铸, 包 博, 杨 韵, 段秦尉

(1.广东电网有限责任公司电力调度控制中心, 广州 510220; 2.中国人民大学应用经济学院, 北京 100872)

2021年7月,国家发改委发布了《关于进一步完善分时电价机制的通知》,要求进一步完善峰谷分时电价机制,减少用电高峰时段的电网运行供应压力,充分发挥电价信号引导电力资源优化配置[1]。各省份积极响应,并根据本省系统负荷特性完善分时电价政策,广东、陕西、重庆、湖南等地峰谷电价比超过4∶1,其中,广东自2021年10月起执行新的峰谷电价,其峰谷比为全国最大达到4.47∶1[2]。

峰谷分时电价是指根据用户用电需求,将每天的用电时间划分为高峰、平段、低谷三个时段或尖峰、高峰、平段、低谷四个时段,对各时段分别制定不同的电价水平,以刺激和鼓励用户主动改变电力消费行为和用电时段,达到削峰填谷的目的,从而提高电力系统的运行经济性和稳定性。

Peter[3]最早从效率的角度分析和研究了峰谷定价问题,将峰谷定价问题与最优发电能力的选择联系在一起,分固定峰形和移动峰形两种情况,得出了负荷高峰和低谷情况条件下的最优发电能力和相应的电价组合。峰谷分时电价经历了试行及推广期、深化期、全面推行期,峰谷电价的实施对用户、负荷特性产生了显著的影响。袁晓玲等[4]、王宝等[5]、白雪敏等[6]、李陆菌[7]、罗建竹和苏春[8]、王毅等[9]、李建华和周灵刚[10]提出了分时电价下不同用户的用电优化策略。在峰谷电价定价上,顾兵等[11]建立了电力市场下多重因素共同作用的峰谷电价定价模型。黄海涛等[12]提出了一种计及负荷率分档的峰谷分时电价定价模型。谭显东等[13]进行了计及负荷发展和用户行为的分时电价优化研究。黄剑平等[14]提出了一种基于用户成本选择用户范围的分时电价最优策略。李国荣[15]对分时电价时段划分进行调整分析,研究出不同地区用电特点下更能反映用户用电规律的分时电价时段设置。刘浩田等[16]提出了一种基于弹性效应权重的价格弹性矩阵模型,对不同时间段价格影响分别设定权重,并计算出符合居民峰谷电价的激励策略。傅质馨等[17]提出了出双层模型实现家庭能量的优化调度,在结合激励机制的基础下有效降低居民日负荷峰谷差,利于电网调度优化运行。

综上所述,现有峰谷电价制定更多地考虑峰谷时期负荷转移的容量成本、辅助服务成本、输配电成本等成本,这些成本主要基于电力系统的物理运行成本进行评估。然而,随着人们对气候变化和环境保护的认识逐渐深入,以及国家双碳战略和构建新型电力系统背景下促进大规模新能源科学发展及减少电力碳排放势在必行,峰谷电价制定应当考虑峰谷电价政策在减排效果方面的重要作用[18-19],通过合理的峰谷电价设定不仅可以提高电网运行经济性、降低电网的物理成本,还可以减少电力碳排放,当前针对如何考虑电力碳排放的峰谷电价设定研究尚未见有相关报道。

本文通过引入经济学框架模型,设计了一种考虑了电力系统碳排放社会成本的最佳峰谷电价优化模型,考虑了生产者剩余、消费者剩余以及峰谷电价政策在减碳领域的贡献。首先,建立峰谷电价政策制定的总社会收益最大化函数模型,通过构建该优化模型的拉格朗日函数,将该优化问题的极值点求解转化为拉格朗日乘数法求条件极值点,通过详细推导得到峰平谷时电价设定的函数关系式,并结合实际运行数据计算了推荐的峰谷电价比例。

1 模型构建及参数化

1.1 社会收益模型构建

社会效益最优的峰谷价格设定应该反映峰谷电价带来的所有收益或不实行峰谷电价政策所造成的所有损失,这意味着在设定峰谷电价时必须充分考虑峰谷电价为整个电力生产环节乃至整个社会带来的收益。基于此框架,综合电力生产、销售、输配、使用的全流程,本文将峰谷电价的社会收益分成电力系统机会成本、生产者及消费者剩余和碳排放社会成本三个部分,以下分别叙述。

1.1.1 机会成本

第一部分为电力系统机会成本(Copportunity)的减少。峰谷电价的设定可以帮助“平滑”负荷曲线,将部分电力需求从高峰时期转移,进而减少尖峰需求对电力系统造成的物理压力,有利于维持电力系统安全稳定充足供应,减少了输配电过程中的机会成本(Ctransmission+Cdistribution)。在长期中,相对平滑的负荷曲线要求的保供的装机容量更少,可以节省对于电力系统备用容量(Ccapacity)、辅助服务机组(Cancillary)的投资,经济学上将这部分成本定义为机会成本,除了资金净值的节省,还可以转移投资,从而带来社会收益。本部分成本节约在目前峰谷电价制定过程中被广泛考虑,现行峰谷电价比例在一定程度上是基于这部分机会成本设定的。这也是模型第一部分,即峰谷电价的社会收益之一是带来的电力系统机会成本的减少,其中机会成本表示为

Copportunity=Ccapacity+Cancillary+Ctransmission+Cdistribution

(1)

1.1.2 生产者及消费者剩余

第二部分为经济学上对买卖双方福利的衡量:生产者剩余(producer surplus,PS)和消费者剩余(consumer surplus,CS),分别表示在交易过程中卖方和买方获得的收益,在峰谷电价的环境中分别为零售商在卖电过程中获得的利润和电力用户在使用电的过程中获得的效用。生产者剩余和消费者剩余是经济学框架下社会收益的主要构成部分,该数值大小与电力需求和购售电价格有关,可表示为PS(p,q)和CS(p,q)。

1.1.3 碳排放社会成本

第三部分为峰谷电价对碳减排的贡献,这是本文研究的主要创新之处。通过对电力系统边际碳排放因子(marginal emission factor,MEF,即每增加一单位负荷带来的碳排放量)的测算,发现在电力需求高峰时期,电力系统的边际碳排放因子也会随之增加,边际碳排放因子真实反映了电力系统发电结构和发电机组类型的排放强度指标,在碳排放的计算中更具有参考价值。因此,峰谷电价政策带来需求转移的同时,也会带来碳排放强度的减少,即减少了碳排放的社会成本(social cost of carbon,SCC)。

综合上述三部分,执行峰谷电价政策的社会总收益(social surplus,SS)模型可表示为

SS=CS+PS-SCC-Ccapacity-

Cancillary-Ctransmission-Cdistribution

(2)

社会总收益公式(2)中包含着峰谷电价带来的总社会收益由消费者剩余、生产者剩余、减少的碳排放社会成本、减少的装机容量成本、减少的辅助服务成本、减少的输电成本和减少的配电成本组成。该分析框架涵盖了电力生产发输配售全生命周期,同时考虑了经济成本和社会环境成本,是描述峰谷电价社会总收益最完整的框架。

1.2 社会收益模型参数化

接下来需要对社会收益模型即公式(2)进行参数化,写出优化目标和约束的具体形式,分析峰谷电价是如何影响社会总收益(SS)的。

在电力需求曲线的构建上,用β表示构成不同时段电力需求曲线qk的一系列参数,不同时间段的电力需求曲线对数形式为

(3)

式中:βk为k时段的需求价格弹性,反映本时段价格对需求的影响;βk,j为k时段与j时段价格的交叉价格弹性,反映其他时段价格对本时段需求的影响。式(3)意味着每个时间段的电力需求是关于本时段电价和其他时段电价的函数。

对价格的需求曲线积分得到消费者剩余CS(p0,θk,β):

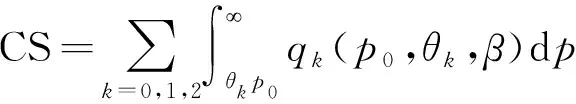
(4)

对需求曲线在批发价格以上、零售价格以下的部分积分得到生产者剩余PS(p0,θk,β):

(5)

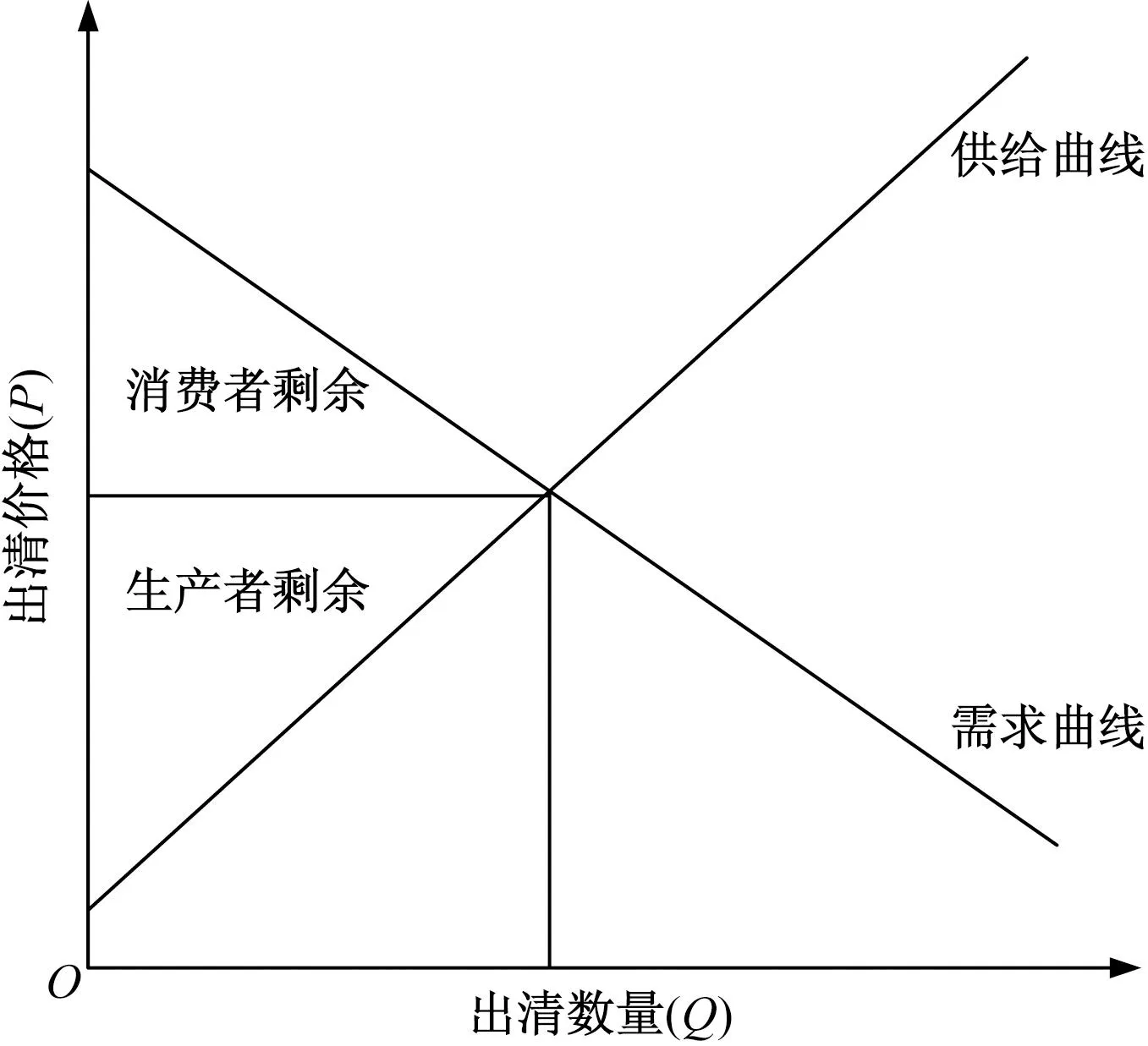
图1 消费者剩余和生产者剩余示意图

SCC(qk)为不同电力需求量带来的碳排放的社会成本,当峰谷电价驱动电力负荷曲线更加平缓时,同时也减少了碳排放的社会成本(SCC),该成本可以通过边际碳排放因子(MEFk)反映,为边际碳排放因子(MEFk)电力消费量qk和碳价Pcarbon的乘积,即

(6)

式中:Pcarbon为碳价;边际碳排放因子(MEFk)的计算过程简述如下:

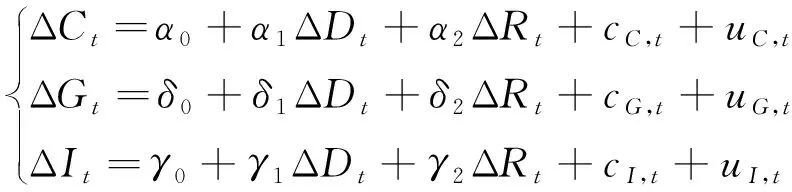
(7)

式中:ΔCt、ΔGt和ΔIt分别为煤电、气电及外受电每小时发电量的一阶差分;ΔDt和ΔRt分别为小时级电力需求及可再生能源发电的一阶差分;α0、δ0和γ0为常数项;α1、δ1和γ1分别为煤电、气电和外受电量对电力需求变化的响应程度;α2、δ2和γ2分别为煤电、气电和外受电量对可再生能源发电变化的响应程度;cC,t、cG,t和cI,t分别为小时级(或更高精度的)电力系统对煤电、气电和外受电量产生影响的其他因素;uC,t、uG,t和uI,t分别为环境噪声变量。运用近似不相关回归模型对式(7)进行估算,可得到参数α1、δ1、γ1的估计值。

由此,可以得到发电系统的边际碳排放因子(MEFk)为

MEFk≈eCα1+eGδ1+eIγ1

(8)

式中:eC、eG、eI分别为煤电机组、气电机组和外受电量的单位碳排放强度(tCO2/MWh)。

通过式(4)～式(6)的参数化模型,可得到峰谷电价政策制定的总社会收益最大化目标函数为

maxθkSS=CS(p0,θk,β)+PS(p0,θk,β)-

SCC(qk)-Ccapacity(qk)-Cancillary(qk)-

Ctransmission(qk)-Cdistribution(qk)

(9)

式(9)中需要确定的参数为峰谷电价的比例θk。

2 拉格朗日乘数法求解

给出目标函数和约束条件,可构建拉格朗日函数来求解参数。在模型(9)中,社会收益最大化的条件为拉格朗日函数的一阶导数为0。由于现在的峰谷电价比例设定主要是基于电力系统的机会成本,假设现在峰谷电价比例已经充分反映了机会成本的Ccapacity+Cancillary+Ctransmission+Cdistribution四部分;在此基础上,聚焦生产者剩余、消费者剩余和碳的社会成本,设置最优的峰谷电价比例。构建拉格朗日函数:

L=CS(p0,θk,β)+PS(p0,θk,β)-SCC(qk)

(10)

式(10)的等式约束条件为式(4)～式(6)。在此,对拉格朗日函数求导并代入约束条件可得

(11)

通过对式(11)第一项进行分部积分变换,得到

(12)

总社会收益目标函数SS极值处,拉格朗日函数导数为0,即执行峰谷电价政策下总社会收益最大化的条件为

(13)

∂qk/∂θk是电力需求对峰谷电价比例的导数,具体而言,由于假设电力需求函数的形式如式(3)所示,可以将该式进一步分解为

(14)

又因为:

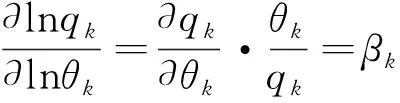
(15)

所以:

(16)

将式(16)带入式(13),得出关于最优峰谷电价比例θk的一次方程,对于每个不同时段的k,有

(17)

βk、qk和θk均不为0,即可得

(18)

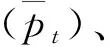
3 算例分析

3.1 边际碳排放因子结果

电力负荷具有显著的分时异质性,按照广东省分时峰谷时段将电量需求样本进行划分,取每日10:00—12:00、14:00—19:00的数据为高峰时段,0:00—8:00为低谷时段,其余时间为平时段。为了揭示电力负荷峰谷碳排放的异质性,使用广东2022年1—3月每15 min的各类型机组出力、需求、西电和现货价格数据,通过似不相关回归分析,估计了基于2021年10月起施行的峰谷电价政策(1.7∶1∶0.38)后,峰谷不同时段广东省燃煤和燃气机组对负荷的响应程度,其结果如表1所示。

表1中回归结果显示当负荷增加时,煤电机组的响应程度要明显高于气电机组,且峰时每增加一单位负荷,煤电和气电机组的响应程度比平时和谷时高30%以上,即在峰时负荷水平增加一单位的碳排放量将比平时和谷时增加一单位负荷的碳排放量高。由于装机容量、调度指标等因素不会在短时间变化,分时峰谷的回归结果更能反映一天内负荷变化造成的碳排放差异。

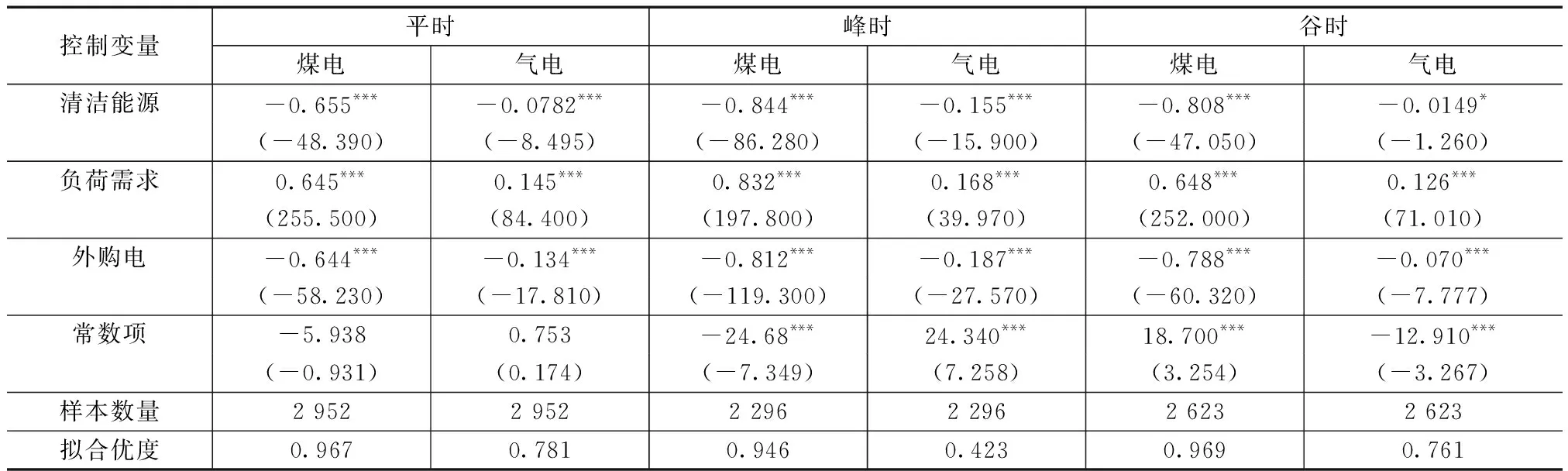
表1 负荷响应回归结果

表2列出了基于近似不相关回归模型估计的峰平谷时段边际碳排放因子MEF的具体数值,可以看出,在不同时段的边际碳排放因子是不同的,高峰时段MEF1明显高于平时MEF0和低谷时段MEF2,对应于表1中对峰谷时段燃煤和燃气机组对负荷的响应程度分析。

3.2 最优峰谷电价比例

计算出各时段的边际碳排放因子MEF后,可以得出在不同电力需求弹性和碳价下的合理峰谷价差。使用广东省2022年1—3月每15 min的电力批发价格和月度电网代理售电价格,结合第3部分的模型和前述边际碳排放因子的回归结果,计算求解考虑了碳排放社会成本的最优峰谷电价调整幅度。在实际计算中,电力批发价格采用广东电力批发市场每15 min的出清价格(该数据保密),峰、平、谷时期的MEF采用表2的结果,Pcarbon参照2022年中国碳市场成交价格设定为49元/t,由于电力零售价格数据保密,本算例中使用2022年1—3月公布的月度电网代理购电价格,如表3所示。

表2 广东省2022年峰平谷的边际碳排放因子

基于表3中数据,可以计算出峰、平、谷时期的平均电价比率,分别为1.089 73、1.038 42和0.819 86。将平时比率标准化为1后,峰时、谷时比率分别标准化为1.049 411和0.789 524,即平均峰时价格需较平时上涨约5%,平均谷时价格应较平时下降约21%。由于本计算假设原始峰平谷比例(1.7∶1∶0.38)已经反映了峰谷电价的机会成本,则进一步考虑了碳社会成本的峰平谷价差应由原来的1.7∶1∶0.38进一步拉大为1.784∶1∶0.30,即峰时电价比例可较现有水平提高0.084,而谷时电价可下降0.080,峰谷比例由当前的4.47∶1扩大至5.95∶1,相关结果如表4所示。

表3 2022年1—3月电网代理购电价格

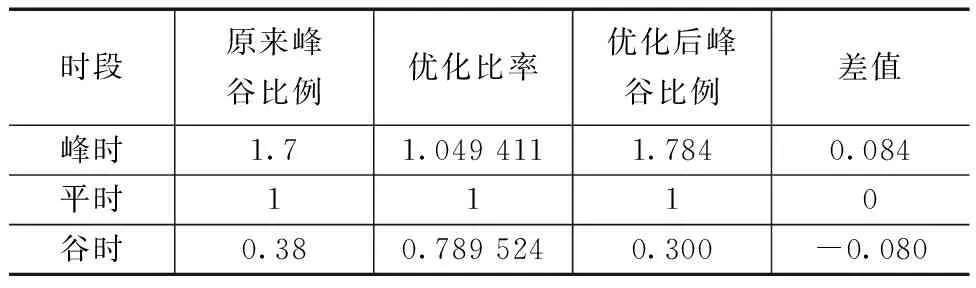
表4 优化后的峰谷电价比例

4 结语

本文针对双碳目标下峰谷电价最优比例设置问题,提出了一种考虑碳社会成本的最优峰谷电价设定方法,通过灵活运用拉格朗日乘数法,将峰谷电价最优比例设置问题转换为求全社会效益最大优化函数极值点拉格朗日函数偏导为0等式约束,从而构建峰谷电价比率与电力批发价格、各每个时段的边际碳排放因子、碳价和电力零售价格关系式。通过广东实际算例,采用似不相关回归分析得出高峰时段燃煤对负荷的响应程度明显高于燃气机组,并首次计算出峰、平、谷三个时段对应的边际碳排放因子,发现高峰时段边际碳排放因子明显高于平时和低谷时段,在此基础上得到计及碳社会成本的最优化峰平谷比例为1.784∶1∶0.3,即在目前峰谷比例4.47∶1基础上进一步拉大电力峰谷电价差至最优值5.95∶1。

基于上述发现可以进一步优化峰谷电价设计,通过峰谷电价和尖峰电价充分引导企业和居民用户在高峰时段尽可能少用电,在低谷时段多用电,不但可以有效减少电网峰谷负荷差,降低电网的物理、运行及调节成本,增加系统经济效益,还可以减少电力碳排放,实现全社会效益最大化。