TBM引水隧洞施工模拟管片力学特性影响因素分析
2024-03-09张建伟李火坤郭新蕾张文远
陈 磊,张建伟,李火坤,杨 帆,郭新蕾,张文远,黄 伟
(1. 华北水利水电大学 水利学院,郑州 450046;2.南昌大学 工程建设学院,南昌 330031;3.中国水利水电科学研究院,北京 100048)
1 概述
随着我国经济的快速发展,引水隧洞工程影响着国民的生活,但引水隧洞在开挖过程中影响管片安全的因素较多[1]。其中引水隧洞顶部的土体深度、周围的围岩类型和加固材料的强度等均会影响隧洞的安全,因此,探究多种因素对引水隧洞管片开挖过程中的力学特性,保证引水隧洞运行期的安全是必要的[2-4]。
当前,国内外学者对于引水隧洞施工模拟技术已取得较多的研究成果。赵首创[5]依托实际隧洞工程,借助数值模拟的方法还原隧洞开挖等过程,开展开挖过程土体的影响范围研究,认为仿真模拟结果较好且开挖过程的土体位移均在安全范围内;吕金辉[6]借助有限元技术,采用上下台阶法开挖,对水工隧洞的位移和应力开展研究,得出开挖过程的围岩位移和应力均满足规范要求且应重点关注开挖区域;Shi C等[7]依托某市地铁盾构开挖工程,提出一种新型盾构隧洞模型,开展不同工况下隧洞管片的应力和位移的研究,得出隧洞开挖中在卸载过程对管片变形较大;张社荣等[8]基于盾构隧道工程,采用有限元法,建立三维非连续接触模型,探究管片变形及螺栓受力的过程,得出不同开挖步骤下管片变形规律基本一致,管片拱顶沉降,拱底隆起的现象;莫键豪等[9]基于某地区输水隧洞工程,开展单层衬砌原位试验研究,揭示了管片在不同内水压力下承载变形特征,得到了管片变形随内水压力的增加而增大且逐步呈现向外的趋势;周济芳等[10]针对引水隧洞TBM施工方法,选取大量研究数据进行论证,得出围岩强度、变形和耐磨性均可采用该方法进行施工;陈克霖[11]依托引大济湟工程,采用仿真软件,模拟引水隧洞施工过程,开展水位、孔隙压力和埋深等因素对隧洞开挖的影响研究;王永德等[12]借助软弱底层盾构隧道工程,采用数值模拟的方法,开展盾构施工过程管片圆周应力的变化规律研究,得出管片的最大、最小主应力随着管片环数的增加而逐渐减小的趋势。综上可知,目前对于水工隧洞施工过程的研究仅进行仿真模拟和方法预测,未探究多种因素对引水隧洞施工过程中管片力学特性变化规律的影响。
针对不同影响因素,借助榕江-关埠引水隧洞工程资料,建立相应的三维有限元模型,开展TBM引水隧洞施工模拟管片受力变形的研究,分析不同因素对引水隧洞施工期管片受力变形变化规律的影响。研究结果可为类似的TBM施工工程提供依据和参考。
2 基本原理
2.1 引水隧洞围岩体地应力平衡
探究引水隧洞施工模拟等研究,首先要进行围岩体初始地应力的模拟。实际工程中围岩体经过长时间的沉降,自身会形成地下应力场,如何模拟围岩体周围的初始应力场是研究隧洞工程合理性的关键[13-14]。
根据大多数引水隧洞工程实例,引水隧洞地表起伏较大及埋深大的区域,水平地应力明显较大,围岩体的构造应力影响更高。本研究的区间段地形平坦、埋深小,围岩体水平向构造应力不突出,自重应力影响较高,因此本次研究仅考虑围岩体的自重应力场[15]。依据工程勘测的地质图,建立该工程典型段的有限元模型。在模拟围岩体初始地应力场时,仅考虑围岩体重力所产生的初始地应力场,其地应力理论解为:
σz=ρgH
(1)
式中:
σz——竖向地应力;
σx——水平地应力;
ρ——围岩的密度;
μ——泊松比;
H——引水隧洞距地面高度。
在数值模拟分析隧洞开挖工程问题时,初始地应力的模拟是计算中的关键问题之一。在有限元计算时需要满足两个条件:
1)隧洞周围应力平衡条件。由应力场形成的等效节点荷载要和外荷载相平衡,如果隧洞周围应力平衡条件得不到满足,将不能提供一个真实的的初始状态,此时所对应的应力场也不再是所施加的初始应力场。
2)隧洞周围单元屈服条件。若通过直接定义高斯点上的应力状态的方式施加初始应力场,常常会出现某些高斯点的应力位于屈服面之外的情况。
在有限元分析软件中,在第一步设置相应的分析步可作为地应力场的平衡,该步骤为岩石工程分析的第一步。在该步骤中,对隧洞周围的土体单元施加对应的体积力,理想状态下,该作用力与土体的初始地应力平衡,使得围岩体单元3个方向位移的数量级减小到10-5m,即此有限元施加第一步初始地应力平衡结果可以接受,对后续的隧洞开挖分析操作无影响。
2.2 岩体摩尔库伦本构
为真实反映围岩体的真实材料,数值模拟中常采用摩尔库伦(Mohr-coulomb)模型屈服准则,借助本构关系来体现岩石的剪切破坏。模型的破坏包络线和Mohr-coulomb强度准则(切屈服函数)以及拉破坏准则(拉屈服函数)相对应。本次计算采用Mohr-coulomb本构模型来模拟围岩石体[16]。
1)增量弹性法则
在Mohr-coulomb屈服准则中,借助了力学中主应力σ1、σ2和σ3,以及平面外应力σzz。主应力和主应力的方向可以通过应力张量分量得出:
σ1≤σ2≤σ3
(2)
对应的主应变增量Δe1、Δe2和Δe3分解如下:
(3)
式中,上标e和p分别指弹性部分和塑性部分,且在弹性变形阶段,塑性应变不为零。
根据主应力和主应变,胡克定律的增量表达式如下:
(4)
式中:α1=K+4G/3;α2=K-2G/3。
2)强度准则
由Mohr-Coulomb屈服函数可以看出A点到B点的破坏包络线图为:
(5)
B点到C点的拉破坏函数如下:
ft=σt-σ3
(6)
式中:
φ——内摩擦角;
c——粘聚力;
σt——抗拉强度。
(7)

(8)
3 仿真模型建立及计算方案
3.1 仿真模型建立及材料参数
以榕江-关埠引水工程输水隧洞段为研究对象,其施工方式以TBM开挖为主[17]。该工程是以城市供水为主要任务,兼顾灌溉的综合水利工程。输水隧洞段地质条件复杂,以Ⅱ、Ⅲ类围岩为主,夹杂少量Ⅳ、Ⅴ类围岩,主要以粗粒黑云母花岗岩为主,地质构造简单,且全风化夹强风化岩状较多。选取该工程的典型区间段,建立精细化三维有限元模型(见图1)。其中管片环模型由4组管片拼接组成,管片环内径为4.3 m,外径为4.8 m,长1.4 m,纵向采用螺栓进行连接;管片内部采用钢笼式-半环加固法铺设内张钢圈,钢环宽600 mm,厚20 mm,排距为1.4 m,管片与内张钢圈之间为环氧树脂(厚10 mm);管片以外的结构依次是豆粒石层(厚0.18 m)、固结灌浆层(厚5 m)、围岩体。数值模拟计算中,除锚杆和化学螺栓采用线单元,其余部件采用三维实体单元,锚杆,并赋予具体的材料参数,其相应力学参数见表1所示。地基域X向、Y向和Z向(竖直向)均以隧洞中心点为起点分别向左、向右、向下延伸5倍洞径,隧道开挖方向长度为14 m。模型网格主要以规则六面体单元为主,整个模型共划分单元65 344个,单元节点77 853个;其中围岩体与注浆层、注浆层与豆砾石、豆砾石与管片等之间采用面面接触,法向“硬”接触,切向摩擦接触,摩擦系数为0.5。隧洞围岩采用Mohr-Coulomb屈服准则,钢筋混凝土衬砌视为弹性体。模拟计算的边界条件设置为:模型围岩前后边界约束Y向位移,左右边界约束X向位移,竖直方向即底面施加完全固定约束。

表1 有限元材料计算参数

a 有限元整体模型
3.2 计算工况
为探究多因素对TBM引水隧洞施工期管片应力位移的影响程度,以各个因素为不同试验工况,具体信息见表2所示,表2中各围岩类型的材料属性见表3。

表2 TBM隧道施工期计算工况

表3 相关参数的物理力学参数
3.3 地应力平衡分析
引水隧洞未开挖前需要进行初始地应力场平衡。由图2~图3可知,围岩体初始地应力场的Z向位移为28.57 mm,若模拟隧洞开挖情况不使用地应力平衡方法,其模拟结果与实际情况不符;采用地应力平衡法后,其围岩体平衡前后应力不变,最大值为1.9 MPa,且平衡后的Z向位移为1.732×10-5m,计算结果能够符合工程精度要求。
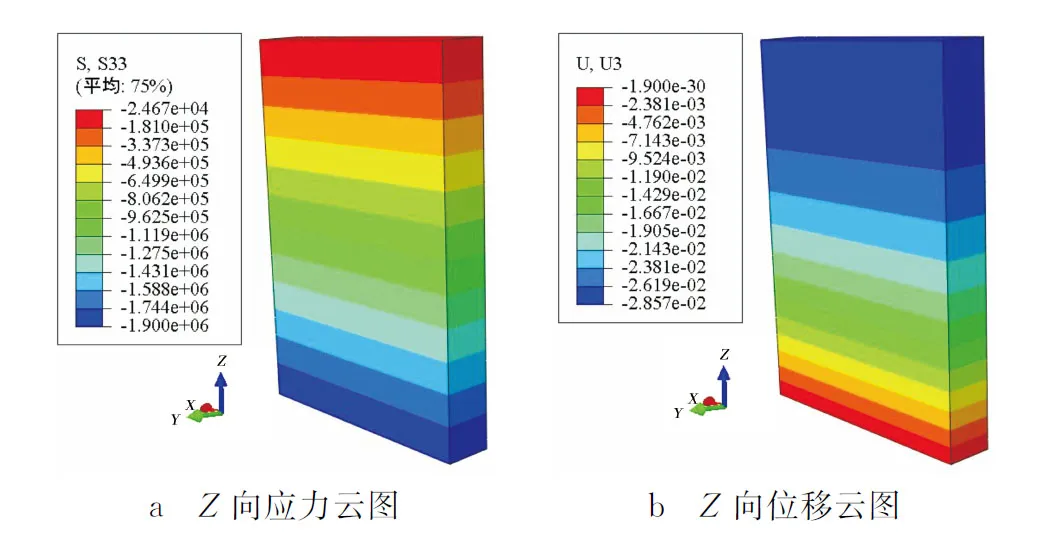
图2 引水隧洞地应力平衡前结果示意

图3 引水隧洞地应力平衡后结果示意
4 多因素对TBM引水隧洞施工模拟管片的影响分析
为探究不同影响因素对引水隧洞施工期管片力学特性的影响。本研究模拟了管片环随着TBM开挖前进的动态变化过程,提取不同开挖步数下,第一环管片的最大位移和最大、最小主应力。为消除边界影响,提取第一环靠内部管片的应力和位移,具体位置见图4。

图4 管片结果位置提取示意
4.1 不同因素对TBM引水隧洞开挖模拟管片位移的影响
4.1.1隧洞埋深对开挖模拟管片位移的影响
不同隧洞埋深下管片位移随引水隧洞开挖环数的变化曲线如图5所示。由图5可知,管片竖向位移随着开挖环数的增加而增大,当隧洞开挖环数在1~4步时,不同埋深下管片的竖向位移增加较为明显,在5~10步时,该环管片的竖向位移上升缓慢。不同隧洞埋深下管片竖向位移最大值分别为0.520 mm、0.811 mm、1.088 mm、1.390 mm和1.670 mm,工况5(埋深为61 m)比工况2(埋深为20 m)的管片竖向位移增加了68.9%,说明管片竖向位移随着隧洞埋深的增大而增大;隧洞埋深为20 m时,管片位移从开挖第1步到第10步增大了59%;隧洞埋深为61 m时,管片位移从开挖第1步到第10步增大了91.7%;说明隧洞埋深增大会增加施工开挖对管片竖向位移的影响效果。因此,TBM开挖围岩体时,对于隧洞埋深较大的工况应重点监测。
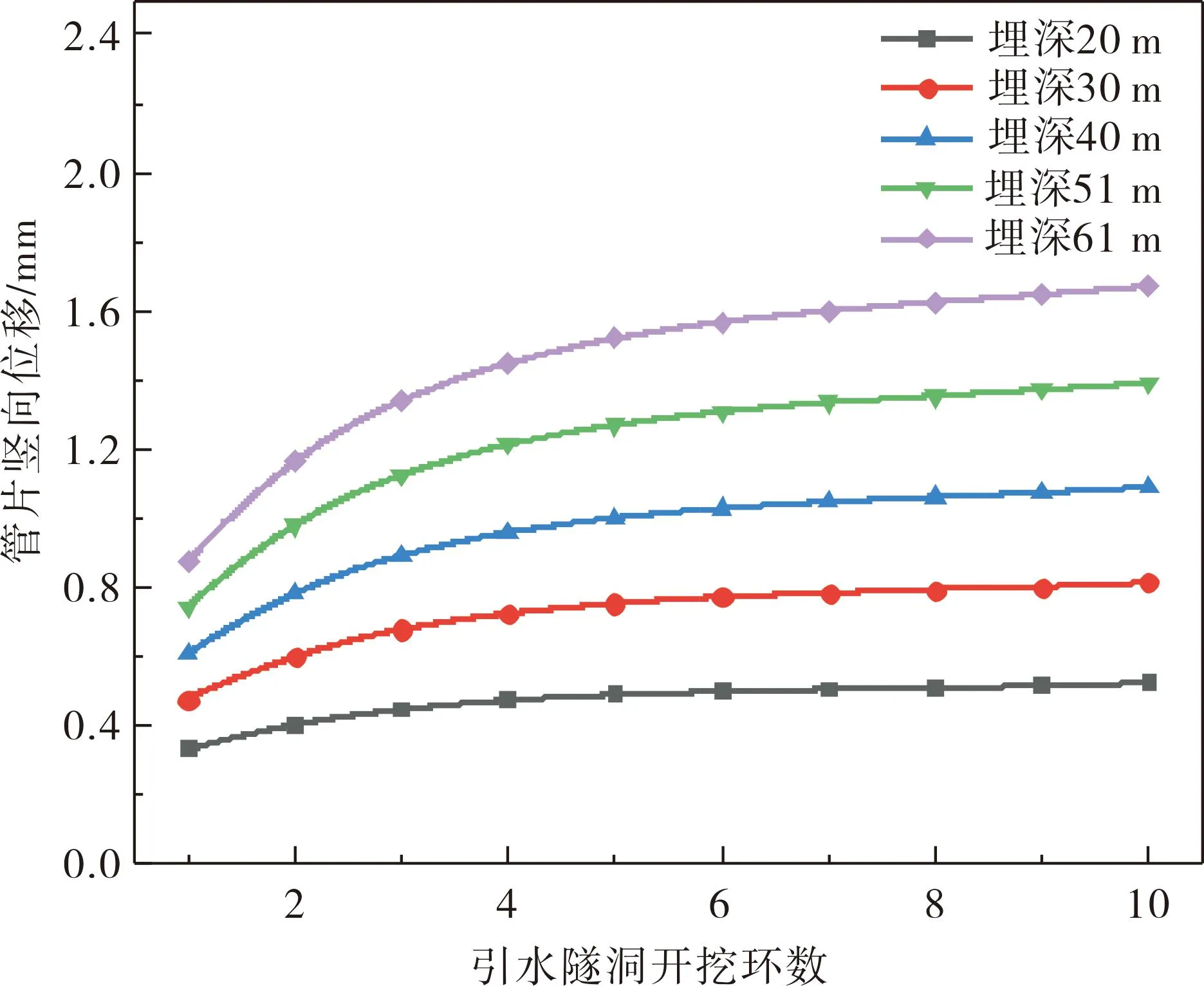
图5 不同隧洞埋深下开挖环数与管片位移关系示意
4.1.2围岩类型对开挖模拟管片位移的影响
不同围岩类型下管片位移随引水隧洞开挖环数的变化曲线如图6所示。由图6可知,管片竖向位移随着开挖环数的增加而增大,当隧洞开挖环数在1~3步时,不同埋深下管片的竖向位移增加较为明显,在4~10步时,该环管片的竖向位移上升缓慢。不同围岩类型下管片竖向位移最大值分别为0.902 mm、1.224 mm、1.390 mm和1.406 mm,工况4(Ⅴ类围岩)比工况8(Ⅱ类围岩)管片竖向位移增加了35.8%,说明管片竖向位移随着围岩质量的削弱而增大;围岩类型为Ⅴ类时,管片位移从开挖第1步到第10步增大了87.8%;围岩类型为Ⅱ类时,管片位移从开挖第1步到第10步增大了55.2%;说明围岩质量增大会减小施工开挖对管片竖向位移的影响效果。因此,TBM开挖围岩体时,对于围岩质量差的工况应重点监测。

图6 不同围岩类型下开挖环数与管片位移关系示意
4.1.3注浆体刚度对开挖模拟管片位移的影响
不同注浆属性下管片位移随引水隧洞开挖环数的变化曲线如图7所示。由图7可知,管片竖向位移随着开挖环数的增加而增大,当隧洞开挖环数在1~5步时,不同埋深下管片的竖向位移增加较为明显,在6~10步时,该环管片的竖向位移上升缓慢。不同注浆属性下管片竖向位移最大值分别为1.099 mm、1.276 mm、1.390 mm、1.523 mm和1.863 mm,工况9(注浆体刚度为3 GPa)比工况12(注浆体刚度为6 GPa)的管片竖向位移增加了41.0%,说明管片竖向位移随着注浆体刚度的减小而增大;注浆体刚度为3 GPa时,管片位移从开挖第1步到第10步增大了91.3%;注浆体刚度为6 GPa时,管片位移从开挖第1步到第10步增大了84.8%;说明注浆体刚度增大会降低施工开挖对管片竖向位移的影响效果。因此,TBM开挖围岩体时,对于注浆属性的选择应重点考虑。

图7 不同注浆属性下开挖环数与管片位移关系示意
4.2 不同因素对TBM引水隧洞施工模拟管片应力影响分析
4.2.1隧洞埋深对开挖模拟管片应力的影响
不同隧洞埋深下管片应力随引水隧洞开挖环数的变化曲线如图8所示。由图8a可知,当隧洞埋深>30 m时,管片压应力随着开挖环数的增加呈现先增大后平稳的现象;当隧洞埋深≤30 m时,随着开挖环数的增加,管片压应力出现较弱的减小趋势,不同埋深下管片压应力最大值分别为2.117 MPa、2.895 MPa、3.808 MPa、4.853 MPa和5.765 MPa;当隧洞开挖次数在1~4步时,不同埋深下管片压应力增加较为明显,之后该环管片的压应力逐渐趋于平稳状态。由图8b可以看出,当隧洞埋深>30 m时,管片拉应力随着开挖环数的增加呈现先减小后增大,再趋于平稳状态;当隧洞埋深≤30 m时,随开挖环数增加,管片拉应力呈现先减小后平稳的状态,其中开挖该环管片时,所受的拉应力最大,最大值分别为0.270 MPa、0.344 MPa、0.465 MPa、0.574 MPa和0.667 MPa;当隧洞开挖环数在1~3步时,不同埋深下管片拉应力减小较为明显。因此TBM开挖围岩体时,在隧洞埋深较大及开挖初期和末期对管片的应力影响较大,实际工程中应重点关注。

a 管片压应力
4.2.2围岩类型对开挖模拟管片应力的影响
不同围岩类型下管片应力随引水隧洞开挖环数的变化曲线如图9所示。由图9a可知,管片压应力随着开挖环数的增加呈先增加后平稳的趋势,随围岩类型的增强,管片压应力逐渐减小,不同围岩类型下管片压应力最大值分别为3.181 MPa、4.256 MPa、4.518 MPa和4.833 MPa;由图9b可以看出,管片拉应力随着开挖环数的增加呈现先减小后增大,再趋于平稳状态,其中开挖该环管片时,所受的拉应力最大,最大值分别为0.482 MPa、0.591 MPa、0.658 MPa和0.674 MPa;当隧洞开挖环数在1~3步时,不同埋深下管片拉应力减小较为明显。因此TBM开挖围岩体时,在开挖初期和末期对管片的应力影响较大,实际工程中应重点关注。

a 管片压应力
4.2.3注浆体刚度对开挖模拟管片应力的影响
不同注浆体刚度下管片应力随引水隧洞开挖环数的变化曲线如图10所示。由图10a可知,管片压应力随着开挖环数的增加而增大,且随着注浆体刚度的增加,管片压应力逐渐减小,其中管片压应力最大值分别为6.165 MPa、5.233 MPa、4.833 MPa、4.482 MPa和3.919 MPa;当隧洞开挖环数在1~4步时,管片压应力增加较为明显,之后该环管片的压应力逐渐趋于平稳状态;由图10b可以看出,管片拉应力随着开挖环数的增加呈现先减小后增大,再趋于平稳状态,其中开挖该环管片时,所受的拉应力最大,最大值分别为0.712 MPa、0.617 MPa、0.574 MPa、0.536 MPa和0.472 MPa;当隧洞开挖环数在1~3步时,不同埋深下管片拉应力减小较为明显。因此,引水隧洞进行施工时,在开挖初期和末期对管片的应力影响较大,实际工程中应重点关注。

a 管片压应力
5 结语
为探究不同影响因素下TBM引水隧洞施工模拟管片位移和应力的变化规律,以某引水隧洞工程为研究对象,建立对应的有限元模型,模拟实际工程的开挖过程,分析不同因素对管片的计算结果,得出结论如下。
1)采用地应力平衡技术,使引水隧洞周围岩体在平衡前后的S33最大应力相等,最大值为1.9 MPa,岩体平衡后的的最大位移为1.732×10-5m,其计算结果满足工程规定。
2)管片位移均会随引水隧洞开挖环的增加而逐渐增加,在开挖1~4步时,管片位移上升明显,之后趋向于稳定。减小隧洞埋深、增强围岩质量和增大注浆体刚度将会降低管片的位移,其最大值分别为1.670 mm、1.406 mm和1.863 mm。
3)随着引水隧洞开挖环数的增加,管片压应力逐渐增加,拉应力呈先减小后增加的趋势,且隧洞埋深较大、围岩质量较差和注浆刚度较小时,管片的压应力和拉应力均为最大值,其中管片压应力最大值分别为5.765 MPa、4.833 MPa和6.165 MPa,均满足规范要求。因此,TBM引水隧洞施工时,应对埋深大和围岩质量差隧洞工程应重点监测。
