基于神经网络算法的汽车前纵梁碰撞性能优化设计

王甲畏 WANG Jia-wei

（澳汰尔工程软件（上海）有限公司，上海 200070）

0 引言

汽车碰撞安全，关系到乘员和车体的安全。如何提高车体的防撞能力，减少伤害事故，车体的结构设计至关重要。对于汽车安全，随着国家汽车碰撞安全法规的不断升级和行业标准的不断提高，对汽车设计的要求也越来越高。当前我国的相关法规有国标，中汽研的C-NCAP 和中保研的C-IASI。

1 汽车碰撞安全性能开发策略

对于汽车厂家来讲，在车辆设计时，根据车辆星级目标，首先要制定碰撞安全策略，即车身结构采用什么样的变形模式，常见的有两大类，分别称为吸能式和掠过式。所谓吸能式就是碰撞时能量分散至全车身结构来承担，目的是避免仅由部分车身结构来承担碰撞能量吸收工作。所谓掠过式（主要是针对小偏置碰）就是车身会滑出壁障，减少车身的变形，进而车内的碰撞冲击力就大幅减小，乘客生存空间几乎不变形。

对于绝大部分碰撞工况，都是依靠车身结构吸收碰撞时产生的能量来进行乘员保护。由于车身结构的复杂性，对车身不同部位，一般采用不同的吸能策略，通常划分为三个区域：低速行人保护区，相容吸能区和自身保护区。

其中，低速行人保护区，车辆的变形和变形受力都应该比较小，这样有利于保护行人和车辆。相容吸能区，是车辆中速碰撞性能区，碰撞时能量比较均匀地被吸收，尽量降低撞击时的加速度峰值。车身设计时，将前端设计软一些，正面碰撞时的能量靠前端车头的变形来吸收，并通过纵梁将撞击力导入到地板结构中。自身保护区，体现高速碰撞时汽车乘员室具有的自身保护能力，车身结构具有较大的刚度，碰撞时为乘员提供足够的生存空间。

2 局部结构变形模式

在车辆发生碰撞时，根据车身结构特点以及对应的工况，每个车身都有明确的载荷传力路径，每个部件结构形状不同，位置不同，所承受的载荷也会不同。

但是，无论结构形式如何，承受的载荷大小多少，每种结构在局部区域或位置上，变形模式主要分为两种：逐级屈服模式和欧拉屈服模式。逐级屈服变形模式如图1a 所示，它最主要的特点是结构尽可能的发生压溃，极少的折弯。吸收的能量与结构的截面积成正比。欧拉屈服变形模式如图1b 所示，最主要的特点是在压溃的同时，发生了较大的折弯。

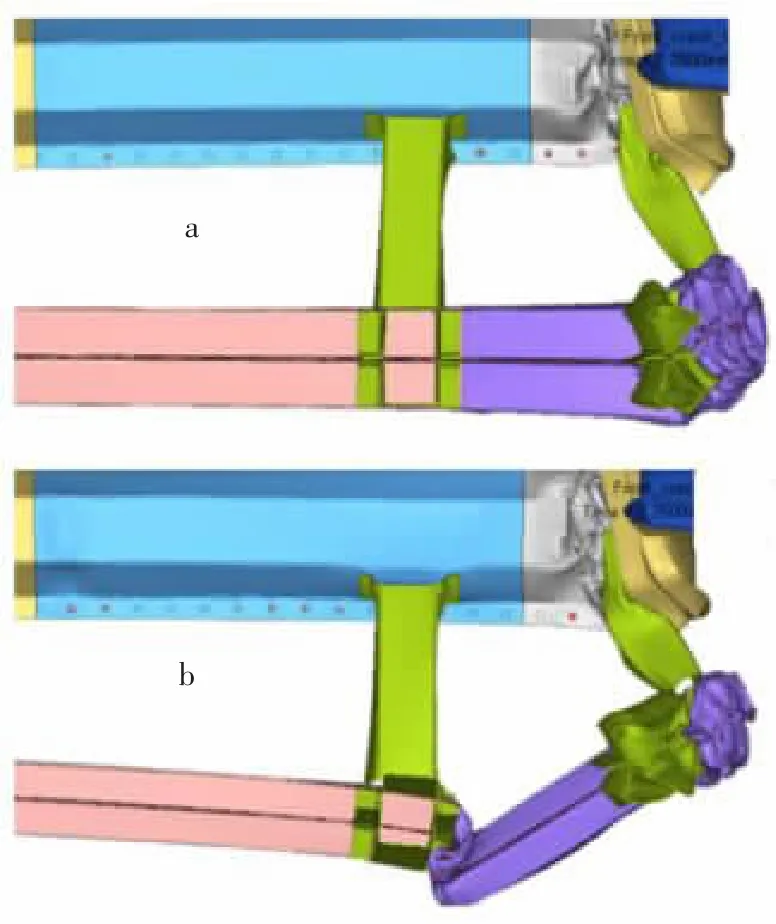
图1 逐级屈服和欧拉屈服变形模式

同样的结构形式，一旦发生了折弯，结构继续承载的能力将大大降低，从而吸能效果也大大折扣。

因此，对于车身结构来说，在绝大部分碰撞工况下，在保证传力路径正常的前提下，都是需要尽可能多的吸收能量，进而给乘员留出安全空间。

3 前纵梁优化设计

本文以某车型前纵梁为例，来描述采用传统的优化设计和基于神经网络模型结合优化设计两种设计方案，并进行结果对比。

3.1 基础设计及碰撞变形模式

前纵梁的基础设计如图2 中a 所示，可以看出，根据设计经验，已经做了一些开孔和加强筋。但是根据100%正碰有限元模型①仿真计算结果可见，如图2 中b 所示，整个结构发生了严重的折弯。

图2 前纵梁基础设计和100%正碰变形结果

3.2 前纵梁优化设计

在结构的优化设计中，有非常多的优化方法，比如拓扑优化，形状优化，尺寸优化，形貌优化[1]等，根据本文的目的，本章节只介绍形状优化方法在前纵梁碰撞工况下的应用。

形状变量：在有限元仿真模型中，主要是通过变化节点的位置，进而带动单元形状的变化，最终形成形状设计变量，优化时，对形状变量定义上、下限范围[1]。

在HyperMesh 中，可以非常方便的通过HyperMorph功能来定义形状变量[2]，本算例中实际定义了47 个变量，主要是在前纵梁上设置一些凹槽加强筋，其目的是希望碰撞发生时在凹槽处发生压溃，图3 为形状变量部分示例，代表凹槽所在的位置。

图3 前纵梁形状变量

本算例的约束条件是：

Internal Energy@200mm > 7.5kJ（在碰撞200 毫秒时，内能大于7.5 千焦）；

Max Force ＜ 120kN。

目标函数是：

其中，xi为设计变量凹槽的深度。

在优化计算时，是把前纵梁放置在整车模型中，其它部件也作为设计变量和对应的约束条件。另外还考虑其它属性，如NVH。因此采用的是多学科优化，在HyperStudy中运行，优化算法采用的是传统的全局响应面法GRSM[3]。

优化后的结果如图4 所示，变形模式（传统优化设计）比基础设计有了改善，但还是发生了一些折弯，与图1 中a 的逐级屈服模式有一定差异，需要继续优化改进。

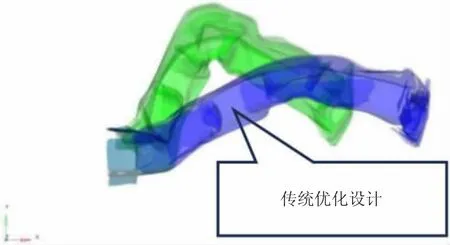
图4 前纵梁优化后变形模式

3.3 神经网络算法与传统优化算法结合

在传统的优化算法中，虽然定义了47 个形状变量，目的是诱发前纵梁产生逐级屈服的变形模式，但因为整车结构复杂，每个部件之间受力相互传递，最后在整车碰撞分析中就难以保证达到想要的设计预期效果。

另外，碰撞计算后的变形模式是由人为来判定的，即发生的结果是折弯还是压溃，是基于变形后的结果，依靠人的经验给出的判定。借助于机器学习（神经网络）算法在图像识别方面的应用，本文把神经网络算法引入到模型结果变形模式的判断中，筛选出最想要的变形模式（本文选择是逐级屈服模式），然后再进行结构优化。

下面内容描述整个算例的过程和方法：

3.3.1 实验设计

实验设计（DOE：Design of Experiment）是一种研究输入参数与响应关系的方法，目的之一是以最少的计算次数研究参数的影响，本文采用的实验设计方法是修正的可扩展格栅序列法（MELS：Modified Extensible Lattice Sequence）[3]。

对前纵梁，选择节点位移为输出结果，为后续机器学习算法来识别其变形模式。本算例选择前纵梁上所有150个节点，每个节点有x，y，z 三个方向，共计450 个位移值，同时结合其它变量，共形成200 个计算。在DOE 结果中，选择输出前纵梁的变形图，参考图2 中b 结果。

3.3.2 数据标签

在HyperStudy 中，以其自带的算法，对DOE 的每种变形图结果进行打标签[3]，一般标注为：Bad, Good, Medium，图5 为示例，共计200 组数据。

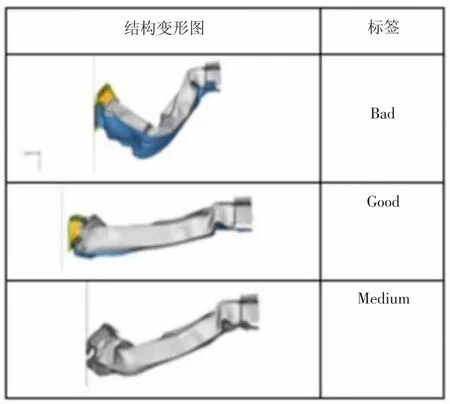
图5 结构变形数据及标签结果

3.3.3 聚类分组

根据标签后的数据，进行聚类分析，很容易的就可以把同类型的变形模式分组，并结合后续优化的计算量，最终分为三组，如图6 所示，左侧106 种的组1 以折弯变形模式为主，中间39 种的组2 以压溃为主，右侧55 种的组3 具有折弯和压溃的组合，本算例中，最后选择中间组2变形模型继续做优化，以提升碰撞性能。

图6 变形模式分组

3.3.4 最终优化

优化目标与3.2 章节一致，除了包含3.2 章节两个约束条件之外，增加一条：

Probability of Cluster 2 > 0.9

这个约束条件的目的是最终结构变形模型发生的可能性要大于90%。

最终的优化结果如图7 所示，比采用传统优化设计的变形模式更加满足设计预期，基本上是逐级屈服模式，达到了设计目的。

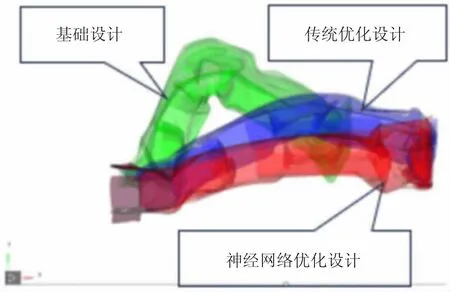
图7 三种设计方案对比

4 小结

本文通过对比传统结构优化算法与基于神经网络+优化算法的两种方法，在前纵梁碰撞性能设计中，采用神经网络+优化算法结合的方法，可以代替人为经验判定，并且在设计时就可以控制结构的变形模式，进而对最终的碰撞性能有更准确的把控和预期，丰富了设计手段。同时，这种方法在汽车其它的结构设计时也得到了很好的验证，说明此方法可靠、可信，有很高的实践价值。

注释：

①本文中的所有结果都是采用有限元仿真计算所得，整车有限元模型采用HyperMesh 建立，求解器采用Radioss 计算，关于模型建立和计算，此文不再详细描述。