基于贝叶斯网络的百色市生态环境综合评价与预测

莫定源 MO Ding-yuan

（百色学院数理科学与统计学院，百色 533000）

0 引言

百色市于2020 年3 月30 日被国务院批复同意设立为广西重点开发开放试验区，这对区域经济快速发展提供了契机，而城市发展也给生态环境带来必然的压力，生态环境污染、生态系统损害的问题将日益凸显。本文开展百色市生态环境综合评价研究，目的在于识别影响百色市生态环境的关键驱动因子，探究各类生态环境指标对生态环境的影响程度及指标间强弱的耦合关系，丰富和发展现有的百色市生态环境评价理论。

目前针对生态环境的综合评价研究包括以下两类：①对生态环境评价指标体系的构建及指标变化趋势的定性研究，研究对象涉及省域、市域、山区道路、矿区、草原等；②基于研究区构建生态环境评价指标体系，并利用统计数据或提取的指标数据，运用相关数学模型对生态环境质量评价进行定量研究。譬如蔡文博等[1]基于遥感多源数据和统计数据对全球四大湾区生态环境进行综合评价，郁文等[2]综合运用层次分析法以及模糊综合评价法对矿山地质的生态环境进行评价，刘璐[3]利用遥感指数法研究河套平原绿洲的生态环境状况，吴倩[4]基于遥感与GIS 技术对华北油田中部地区进行生态环境评价，盖美等[5]基于熵权TOPSIS 法探究海洋生态环境质量状况。此外，也有学者将贝叶斯网络模型应用于生态环境领域，譬如黎斌等[6]提出运用贝叶斯网络对城市生态红线进行划定，杨湘艳等[7]基于贝叶斯网络对海洋生态环境质量进行评判。虽然众多学者对生态环境的评价进行了研究，但鲜有学者以市域为研究对象进行生态环境质量的预测研究。另外，在进行生态环境综合评价时，存在指标体系构建欠妥、数据质量难以保证以及对生态环境系统认知受限等问题，影响了生态环境的综合评价结果的客观性和准确性。

本文在前人研究的基础上，构建百色市生态环境综合评价指标体系，并建立基于贝叶斯网络的百色市生态环境综合评价模型，该模型的优点是可以弥补生态环境综合评价过程及预测的不确定性，在某种程度上提高评价结果的准确性及预测的可靠性。利用贝叶斯网络直观、可视化的特点，可以直观揭示指标间的依赖关系。此外，利用贝叶斯网络强大的推理能力，结合生态环境系统的内部作用机理，充分挖掘各要素间蕴藏的潜在关系，并对百色市生态环境质量进行预测研究。

1 生态环境综合评价模型

1.1 贝叶斯网络相关理论

贝叶斯网络（Bayesian network，简称BN）是利用图模型表示概率知识的模型，己经成为解决不确定性问题进行有效表示、概率推理、结构学习和参数学习的有效工具之一[8]。BN 是一个有向无环图，由网络拓扑结构和条件概率表构成。其理论依据是概率统计中的贝叶斯公式：

上式中，将X=x 视为假设，Y=y 视为证据。在输入证据Y=y 之前，P（X=x）称为先验概率，在输入证据Y=y 之后，P（X=x｜Y=y）称为后验概率[9]。贝叶斯网络可以有效融合专家先验知识和证据信息，新证据输入模型后能对先验概率进行修正，各节点能得到更符合客观事实的概率分布。

假设V={x1，x2，…，xn}表示随机变量的集合，E 表示节点间的相互依赖关系，P 表示模型中的条件概率表，则贝叶斯网络模型可表示为B=＜G，P＞。根据统计学概率论的相关知识，贝叶斯网络联合概率分布则可表示为[10]：

根据马尔可夫理论，若已给定父节点集的情况下，则该节点独立于其非后继节点。记β（xi）表示节点xi父节点集，则：

通常，确定节点的有向弧（即网络的拓扑结构）的过程称为结构学习，而确定节点间相互依赖程度（即条件概率表CPTs）的过程称为参数学习，将二者统称为贝叶斯网络学习。计算贝叶斯网络节点后验概率的过程称为贝叶斯网络推理，是实现模型预测、诊断分析、评估系统的理论依据[9]。

1.2 基于贝叶斯网络评价模型的构建

本文将贝叶斯网络模型应用于生态环境综合评价，融入专家知识和实证数据，建立指标间的贝叶斯网络拓扑结构，并利用实证数据进行参数学习、敏感性分析，再通过贝叶斯概率推理进行生态环境预测研究。本文构建的基于贝叶斯网络的生态环境综合评价模型如下：

上式中，Y 表示子节点生态环境综合指数（i 表示生态环境综合指数等级，本文中设置该节点为三个等级，在贝叶斯网络中也称为三个状态，分别为良好、一般、较差）或者准则层指标指数。X 表示父节点准则层指标或指标层指标。xj表示第j 个指标的观测值。

利用本模型进行生态环境综合评价与预测，步骤如下：①针对研究区独特性的地理位置、气候、经济状况等，筛选合适指标构建综合评价指标体系；收集指标数据及计算相关指标数据，并对数据进行标准化处理、等级划分等；②利用AHP 方法、熵值法二者组合最终确定指标权重；③根据指标间的因果关系或依赖关系，并咨询相关领域专家，确定贝叶斯网络拓扑结构示意图；④利用Netica 软件基于实证数据对贝叶斯网络模型进行参数学习；⑤对参数学习后的模型进行验证，并对感兴趣节点（生态环境综合指数）进行敏感性分析；⑥利用贝叶斯网络强大的推理能力，设置因果推理及诊断推理，挖掘指标间潜在的强弱耦合关系，对2013-2020 年百色市生态环境质量进行评价，并对预测结果进行综合分析。

1.3 综合评价指标体系构建

本文以百色市为研究对象，依据目的性、整体性、主导性、动态性和相关性等原则，结合百色市独特的地理位置、气候特点等，筛选合适指标并确定百色市生态环境综合评价指标体系（表1），本文所用到的数据主要来源于《百色市国民经济和社会发展统计公报》（2013-2020）、《广西统计年鉴》（2013-2020）、《百色市统计年鉴》（2013-2020）、广西百色市生态环境局官网等。所用指标的部分数据，是经计算整理后得到。

表1 百色市生态环境综合评价指标体系及指标代码

1.4 数据处理与权重确定

目前，确定指标权重的方法主要有两类：一类是客观法，另一类是主观法。本文为了避免受主观因素影响较大，同时也为了消除对数据的过度依赖，采用AHP 法和熵值法二者混合最终确定指标的权重。AHP 方法的具体计算步骤详见相关参考文献[11]。

熵值法计算步骤如下：

①假设样本数据可以用m 行n 列的矩阵表示，即

②数据标准化处理，计算公式如下[12]：

正向指标：

负向指标：

由xij组成标准化矩阵。

③计算上述标准化矩阵第j 项指标下第i 个记录所占比例：

由yij组成矩阵。

④计算上述矩阵Y 第j 项指标的熵值：

⑤计算差异性指数hj。令hj=1-Ej，则当hj越大时，该指标对评价作用就越大。计算hj占总体的比重，计算方法为：

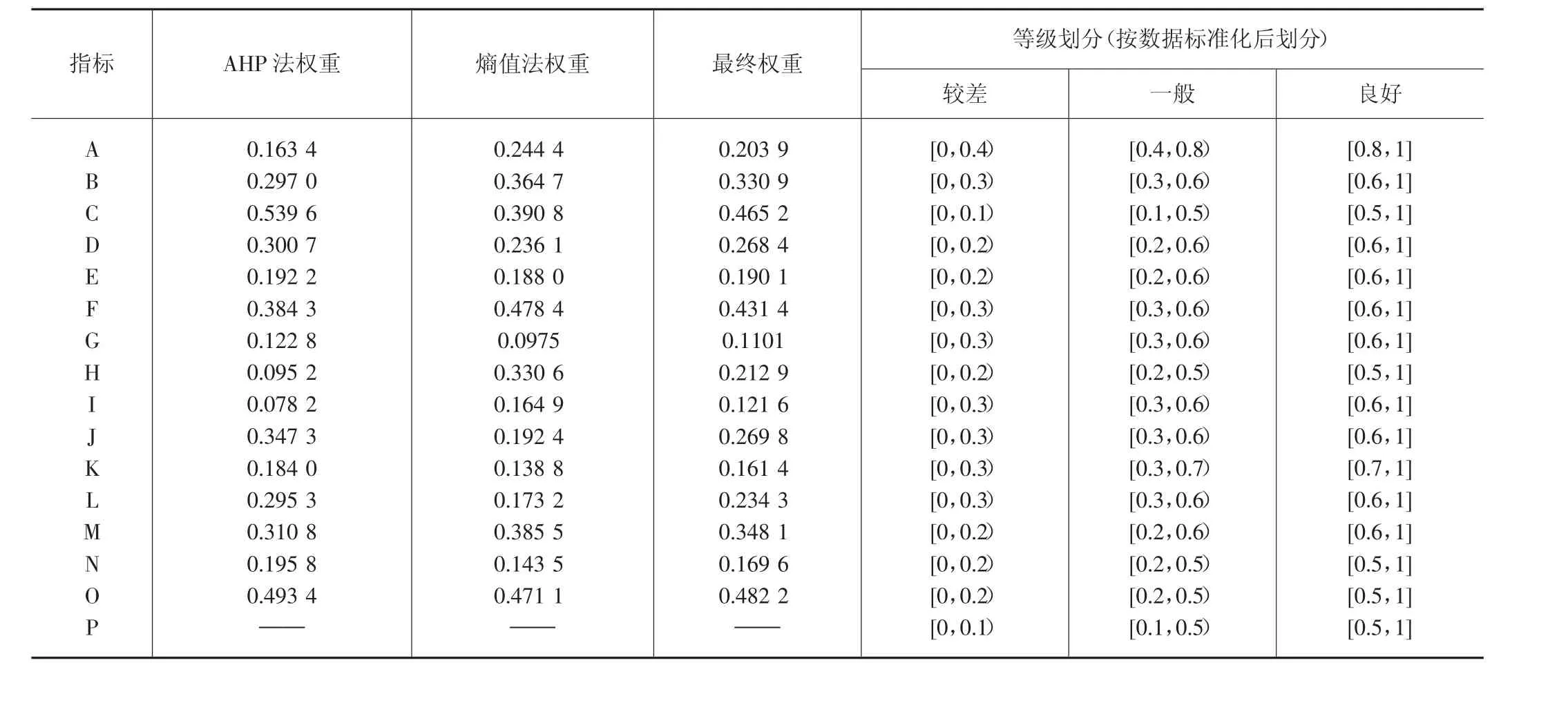
表2 百色市生态环境综合评价指标权重及等级划分

下一步，利用综合指数法计算准则层和目标层数值，综合指数法公式如下：

上式中，W 表示某一年的生态环境综合评价指数或准则层某个指标，Qi表示准则层指标或指标层指标标准化值，Pi表示指标权重，n 表示指标个数。经计算，百色市2013-2020 年各年份的目标层和准则层指标数据如表3所示。依据自然断点法及相关文献研究成果对指标进行等级划分，等级划分结果详见表2。

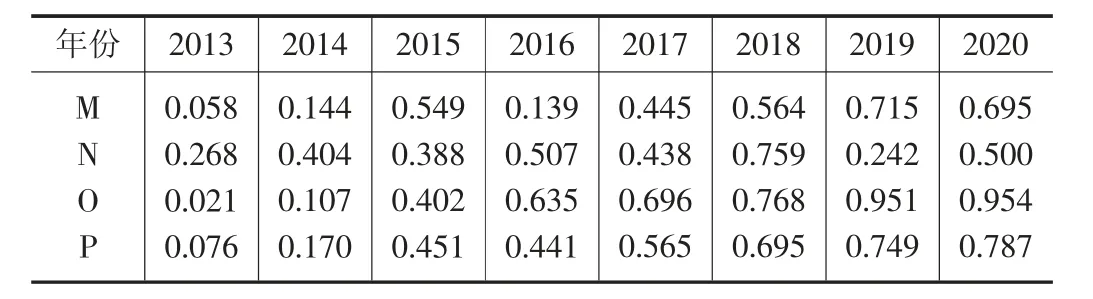
表3 2013-2020 年百色市生态环境准则层、目标层指标标准化数据

2 结果与分析

2.1 综合评价及演变过程分析

为了直观反映百色市2013-2020 年生态环境质量状况，以折线图的形式揭示百色市自然环境指数、生态环境指数、社会环境指数、生态环境综合指数评价结果及演变过程，详见图1。

图1 百色市生态环境综合评价结果及演变过程

由图1 可知，从2013-2020 年，自然环境指数总体呈现上升-下降-上升-下降的趋势，因为2015 年是降水量最多的年份，因此自然环境指数较高，而2016 是降水量最少的年份，导致自然环境指数呈现较大幅度下降。2013-2020 年，生态环境指数呈现曲折上升的趋势，这是因为城市道路面积在增加，对生态环境有明显的负向作用，加剧了生态环境的破坏，而污水处理厂集中处理率、人均公园绿地、生活垃圾处理率都呈现总体上升的趋势，对生态环境有明显的正向作用，在这四个因素的耦合作用下，使得生态环境指数呈现曲折上升的趋势。2013-2020 年，社会环境指数呈现总体上升的趋势，社会环境变得越来越好。主要原因是第三产业占GDP 比值、人均GDP、教育支出均呈现逐年增加趋势，从而促进社会环境质量变好；同时，工业废水排放量、工业二氧化硫产量总体呈现逐年下降的趋势，对社会环境的改善起到很大的促进作用，虽然该两项指标在2020 年有所上升，但在这五个因素的耦合作用下，使得社会环境指数呈现不断上升的趋势。生态环境综合指数除了在2016 年有较小幅度下降，其余年份均呈现不断上升的趋势，表明百色市生态环境质量在不断得到提升。

2.2 贝叶斯网络结构学习

本文以驱动力（压力）-状态-响应为主线构建贝叶斯网络模拟和预测模型，指标层指标作为影响百色市生态环境的直接驱动力，生态环境质量是生态环境受到驱动力影响的状态，而响应是国家、政府部门及个人采取具体措施阻止、减轻生态环境恶化而作出的行为与决策。目前，构建贝叶斯网络结构的方法主要有两种：一是领域专家确定；二是实证数据训练。若通过实证数据学习得到，则必须要有足够的样本数据，而节点间因果关系或依赖关系很明显时，领域专家确定网络拓扑结构更具优势[13]。本文选取的指标依赖关系明显，因而采用领域专家知识方法确定贝叶斯网络拓扑结构，详见图2。

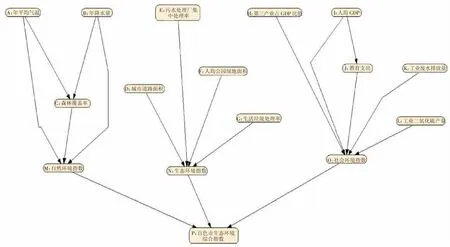
图2 贝叶斯网络拓扑结构示意图

2.3 贝叶斯网络参数学习

贝叶斯网参数学习的目的是为了确定BN 各节点条件概率表（CPTs）。本研究运用Netica 软件EM 算法对贝叶斯网络模型进行参数学习，参数学习后的模型如图3 所示。限于篇幅，现以节点C（森林覆盖率）为例，参数学习后的条件概率表如表4 所示。

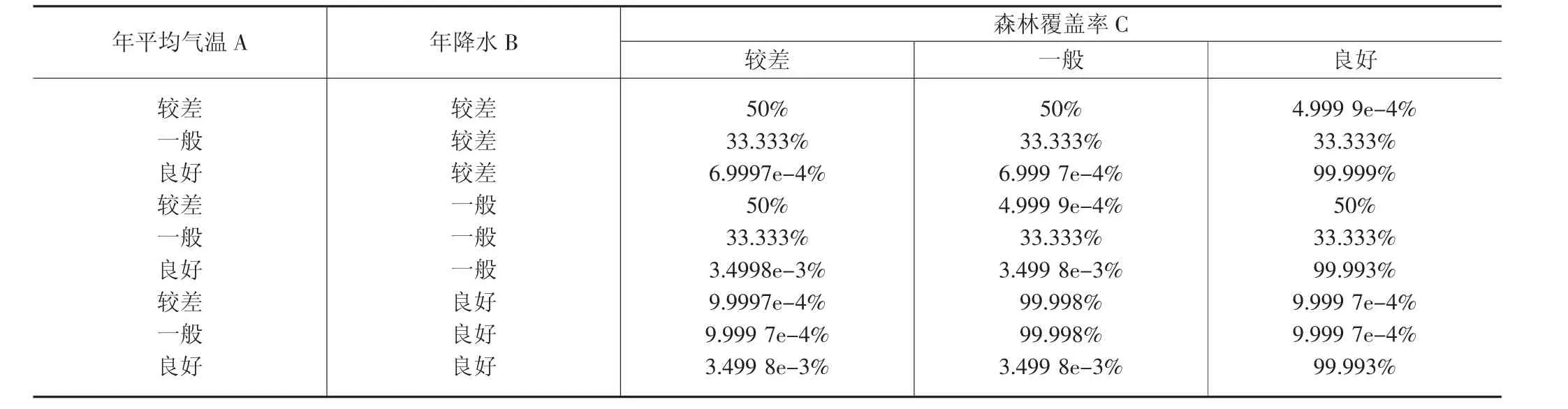
表4 节点C 森林覆盖率参数学习结果

当人类活动过度干预生态环境，干预程度超过生态环境自我修复的阈值时，必将导致生态环境受损。政府部门应当根据不同的生态环境质量等级，采取相应的生态环境政策，以促进生态环境与社会经济的协调发展。现以图3构建的贝叶斯网络模型为例，在贝叶斯网络模型的基础上添加响应模块，图3 中节点U 即为响应节点，模拟政府部门在不同生态环境质量等级下的管理对策，详见表5。

2.4 敏感性分析

贝叶斯网络模型中敏感性分析是通过改变输入节点参数的值来量化目标节点的影响程度[14]，Netica 软件通过方差缩减方法对目标节点进行敏感性分析。方差缩减的值越大，表示该节点对目标节点影响越大；反之，则越小[7]。通过敏感性分析，识别影响百色市生态环境的主要驱动因子，从而为生态环境保护提供理论依据。选择百色市生态环境综合指数作为目标节点，敏感性分析结果如表6 所示。

表6 模型中各指标敏感性分析

由表6 可知，准则层指标对目标节点影响最大的指标依次是社会环境指数、自然环境指数、生态环境指数；在指标层各指标中，对目标节点影响的前五个驱动因子分别是森林覆盖率、年平均气温、年降水量、工业废水排放量、教育支出，表明该五项指标对百色市生态环境质量影响较大。

2.5 模型验证

为了验证模型的稳定性和鲁棒性，参照相关学者[15]的方法对模型进行验证。根据图3 训练的模型，以目标节点（百色市生态环境综合指数）的最大概率所在等级作为最终预测值，并将预测值与综合指数法计算得到的实际值进行比较。

大部分年份预测结果与真实值相吻合，经计算该模型预测准确率为87.5%。根据相关学者的经验，BN 模型准确率高于80%即可表明模型的预测效果较好[16]，因此本文构建的贝叶斯网络模型性能较好，从而可利用该模型进行预测研究。

2.6 推理预测研究

本文在综合考虑敏感性分析、人类活动影响等因素的基础上，从因果推理、诊断推理两个方面设置典型的情景分析。

2.6.1 因果推理

在贝叶斯网络中通过设置父节点的值（输入证据）来推导子节点各等级发生的概率，依据最大概率原理来判断推理的结果。

①单因素对百色市生态环境综合指数的影响。依据敏感性分析，选择对百色市生态环境综合指数影响较大的因素（森林覆盖率）作为典型例子。现通过输入森林覆盖率的证据，对百色市生态环境综合指数的等级进行预测，结果如表7 所示。

表7 单因素对百色市生态环境综合指数等级的预测

由表7 可知，输入证据森林覆盖率为较差时，预测的百色市生态环境综合指数等级为一般；输入证据森林覆盖率为一般或良好时，预测的百色市生态环境综合指数等级为良好。由此可见，在其他变量保持不变时，不断提升森林覆盖率的等级，对百色市生态环境综合指数等级有较明显的提升，从而促进人与自然环境的和谐相处，改善人们的居住环境质量。

②多因素对百色市生态环境综合指数的影响。通过设置与人类活动相关的教育支出、工业废水排放量、工业二氧化硫产量指标的混合证据，基于最大概率原则对百色市生态环境综合指数进行预测研究，结果如表8 所示。

表8 多因素对百色市生态环境综合指数等级的预测

由表8 可知，在其他变量均不变时，输入证据教育支出、工业废水排放量、工业二氧化硫产量指标的混合证据均为较差或一般时，百色市生态环境综合指数的预测等级为一般；在其他变量均不变时，输入证据教育支出、工业废水排放量、工业二氧化硫产量指标的混合证据均为良好时，百色市生态环境综合指数的预测等级为良好。由此可见，随着教育支出的增加，工业废水排放量、工业二氧化硫产量的减少，百色市生态环境综合指数将由一般变为良好。

2.6.2 诊断推理

在贝叶斯网络中通过设置子节点的值（输入证据）来推导父节点各等级发生的概率，依据最大概率原理判断推理预测结果。现输入百色市生态环境综合指数状态三的证据，探讨指标层指标各等级发生的概率，并对比先验概率与后验概率的变化量。结果详见表9。

表9 输入百色市生态环境综合指数状态三证据对指标层指标各等级的概率

由表9 可知，输入证据百色市生态环境综合指数状态三时，变化量排在前十名分别是森林覆盖率状态三、年平均气温状态一、年平均气温状态三、工业废水排放量状态三、教育支出状态三、人均GDP 状态三、年降水量状态三、森林覆盖率状态一、年降水量状态一、工业二氧化硫产量状态三。此外，当百色市生态环境综合指数为状态三时，各指标状态三的概率均有不同程度的提升，由此说明欲提升生态环境的质量，必须不断提升各指标良好状态所占的比例。其中，森林覆盖率指标状态三的概率变化最大，并且预测值由原来的状态二转变为状态三，即为了达到生态环境综合指数为良好等级，则必须保证森林覆盖率也必须是良好等级，这可为地方政府实施政策体系提供一种思路。其他推理研究类似上述讨论，在此不再赘述。

3 讨论

3.1 综合评价与演变过程分析

从图1 可知，社会环境指数与生态环境综合指数的变动几乎趋于一致，表明社会环境指数对生态环境指数影响很大，这与敏感性分析中社会环境指数对生态环境指数影响最大的结论相吻合。同时，在2013-2020 年间生态环境综合指数在不断上升，由此可以看出百色市生态环境质量在不断得到提升，表明政府部门实施的生态环境保护政策已发挥应有的作用。

近年来，百色市为了加大环境保护力度，先后颁布了《百色市环境保护“十二五”规划（2011-2015 年）》《百色市“十三五”工业绿色发展规划》《百色市节能环保产业发展“十三五”规划》等规划方案，这些规划方案对百色市生态环境进行严格监管，对工业废水排放、工业二氧化硫排放、生活垃圾处理、大气污染物排放等方面设立严格的标准，使得百色市生态环境质量得到了明显的提升。在近几年，工业废水排放量、工业二氧化硫排放量等显著下降，生活垃圾处理率显著上升，表明百色市生态环境保护在政府相关部门的监管下已有一定成效。

3.2 基于贝叶斯网络模型概率推理的预测分析

通过构建贝叶斯网络预测模型，可以克服指标体系构建欠妥、数据质量难以保证以及对生态环境系统认知受限等因素的不确定性，贝叶斯网络预测结果并不是绝对的，而是将最大概率所在的状态作为预测值，从而提升了预测结果的客观性、科学性和准确性。通过贝叶斯网络因果推理和诊断推理，可以预测在不同情境下生态环境的变化趋势，为预防环境恶化及生态破坏提供理论依据。

敏感性分析结果表明，对百色市生态环境综合指数影响最大的五个指标分别是森林覆盖率、年平均气温、年降水量、工业废水排放量、教育支出，从诊断推理可知变化量排在前十名分别是森林覆盖率状态三、年平均气温状态一、年平均气温状态三、工业废水排放量状态三、教育支出状态三、人均GDP 状态三、年降水量状态三、森林覆盖率状态一、年降水量状态一、工业二氧化硫产量状态三。从诊断推理结果可知，变化量越大的指标表示受生态环境综合指数影响也越大，即该指标对生态环境综合指数越敏感。通过对比敏感性分析结果与诊断推理结果，二者彼此交融、相互验证：一方面，贝叶斯网络的诊断推理结果充分验证了敏感性分析的正确性；另一方面，敏感性分析结果能为贝叶斯网络推理提供决策支持。

4 结论

本文基于贝叶斯概率相关理论，结合领域专家知识和客观实证数据，构建了基于贝叶斯网络的百色市生态环境综合评价与预测模型，主要结论如下：

①本研究确定各指标权重充分融合了领域专家知识和客观实证数据。AHP 方法确定权重主要基于生态、环境相关领域专家知识，而熵值法权重则基于客观数据，融合两种方法确定指标权重，使得评价结果更加科学、合理。

②对百色市生态环境综合指数进行了贝叶斯网络敏感性分析，从而有效识别影响百色市生态环境的关键驱动因子，可以为政府部门制定生态环境保护政策提供参考。

③基于贝叶斯网络强大的推理能力，通过输入单因素或多因素组合的证据，模拟情景分析进行预测研究，可以充分挖掘模型中潜在的信息。此外，在贝叶斯网络模型的基础上可以添加响应模块，模拟不同管理对策下的效应。

④对百色市2013-2020 年生态环境质量进行综合评价及演变过程分析，结果表明百色市近年来在生态环境保护工作方面已取得一定成效。

百色市生态环境综合评价与预测模型的构建，一方面可以为百色市生态环境保护与社会经济发展协调的政策制定提供科学指导，促进百色市自然、环境、社会等可持续发展；另一方面，利用贝叶斯网络强大的推理能力，可以预测在不同情境下生态环境的变化趋势，为预防环境恶化及生态破坏提供理论依据，发挥动态监测在实践中的有效应用。本文在某些指标数据获取时存在一定困难，导致构建的综合评价指标体系还不够全面。下一步，我们将构建更加完善、全面的生态环境综合评价指标体系，同时融入动态贝叶斯网络模型，进一步提高评价和预测的准确性。