后摆心潜入式喷管柔性接头力学特性数值仿真

龚建良，徐朝起，胥亚亚，白梦雪，古呈辉，许桂阳，杨燕京

（1.西安近代化学研究所，陕西 西安 710065；2.西安交通大学 航天航空学院，陕西 西安 710049；3.甘肃银光化学工业集团有限公司，甘肃 白银 730900；4.山西北方兴安化学工业有限公司，山西 太原 030008）

0 引言

柔性喷管具有偏转能力强、摆动力矩小、密封性好、抗扭刚度好、推力损失小、结构简单、工艺性好等优点，是目前固体火箭发动机推力矢量控制的主要方式，在战术导弹、战略导弹、运载火箭中都有应用，如标准-3 导弹、THARD 导弹和MX 导弹[1-3]。柔性接头作为柔性喷管的关键部件，由前法兰、后法兰、弹性件、增强件组成。前、后法兰采用高强不锈钢材料；弹性件采用高延伸率与低模量的超弹性橡胶材料；增强件采用高强不锈钢或者复合材料。弹性件与增强件相互交替黏接制备而成[4]。载荷形式、动态性能、力学性能、热性能、结构参数、结构形式对柔性接头的工作安全性与可靠性具有重要的影响[5]。

国内外学者针对柔性喷管已开展了相关研究。文献[6]针对固体火箭发动机柔性接头的优化问题，采用了大变形非线性有限元方法，比较分析了等截面与变截面柔性接头的质量、内部应力、变形和动态性能，确定了轻质化变截面柔性接头结构；文献[7]针对柔性喷管在弹射压强载荷下应力分析，采用了轴对称有限元方法，分析了在0.5 MPa弹射压强下，接头内部应力分布，校核了弹性件强度与界面黏接强度；文献[8]针对柔性接头在有限元计算过程中，网格规模大、收敛难的问题，采用了刚-柔混合法，展开了柔性接头摆动力矩、变形分析，计算结果误差小于5%；文献[9]针对柔性喷管在高压下摆动力矩减小的问题，建立了三维柔性接头模型，分析了不同容压下柔性接头内部剪切应力分布，研究表明，弹性件剪切应力变化是引起高压下摆动力矩减小的原因；文献[10]研究了战术导弹发动机柔性接头的摆动特性，采用二阶超弹性模型描述硅橡胶弹性件的材料属性，研究表明，驱动接头转动的力主要是克服弹性件的剪切应力，其径向剪应力远大于纬向剪应力；文献[11]针对小型柔性接头的弹性力矩变化特性，采用试验与数值模拟方法，研究表明，弹性力矩随压力与摆角增大，先下降而后上升；文献[12]研究了增强件数量对柔性接头变形与应力分布的影响规律，研究表明，在增强件总厚度不变情况下，随着增强件数量增加，增强件变形减小、增强件应力上升及增强件失效的风险增加；文献[13]针对战术导弹发动机柔性接头在燃烧室压力与摆角载荷下变形与应力分布的问题，采用有限元方法，获取了柔性接头的变形与应力分布；文献[14]针对二维轴对称的柔性接头模型，研究了增强件弹性模量变化对接头变形与应力分布的影响规律，研究表明，随着增强件弹性模量增大，轴向压缩变形减小；文献[15]针对柔性接头的动态力学特性计算问题，采用模拟退火算法优化模型参数，提高了计算精度；文献[16]针对柔性喷管的动力学仿真问题，采用电液伺服机构-神经网络模型方法，开展了不同摆动振幅、摆动频率、工作压强下动力学特性计算，计算结果与实验吻合较好；文献[17]针对柔性喷管的力矩辨识问题，采用1 种基于遗传算法优化的神经网络方法，准确地描述了柔性喷管在典型测试信号激励下的力矩特性。

可知，针对喷管柔性接头在载荷作用下的变形与应力分布，国内外学者已经开展了相关研究，获取了一些有价值的成果。然而，针对后摆心潜入式喷管在燃气压力、摆动载荷与联合载荷下的变形、应力分布、弹性比力矩等变化规律方面缺乏相关细致的研究，本文拟采用数值分析方法进一步开展此项研究。

1 有限元模型

1.1 几何模型

图1 为后摆心潜入式喷管结构图，其关键部件为柔性接头。柔性接头是由以同心球形状的增强件与弹性件相互交替，以及前、后法兰黏接而成的1个整体部件。它是柔性喷管承受活动体的喷射载荷，同时也是全轴摆动的核心部件。

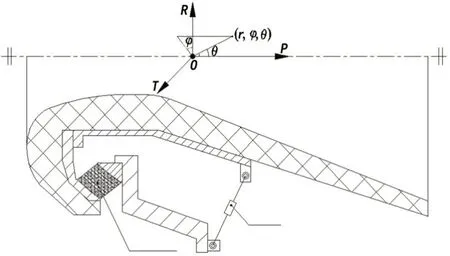
图1 后摆心潜入式喷管结构图Fig.1 Structure diagram of afterward pivot movable nozzle

一般来说，柔性喷管需要经历冷态摆动试验与热态点火试验考核。冷态摆动试验在压力模拟容器中进行；热态点火试验在试车台进行。依据柔性接头在喷管中结构与受力形式，为了模拟柔性接头在摆动过程中的变形与受力，建立了柔性接头几何模型，其由前、后法兰、弹性件、增强件、加压堵盖组成，见图2。

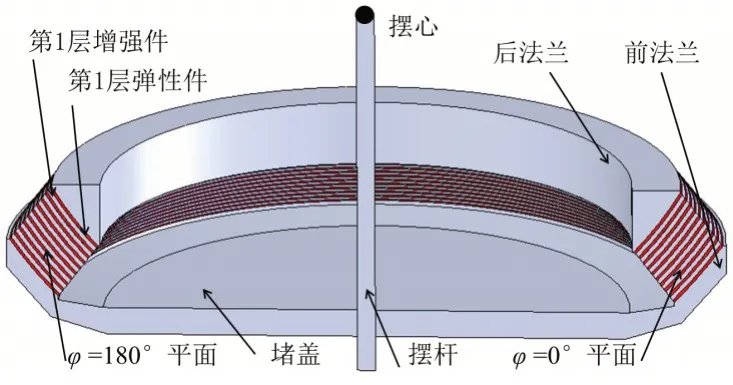
图2 柔性接头几何模型Fig.2 Geometric model of flexible joint

结构化网格具有计算结果准确、计算效率高的优点。柔性接头模型采用结构化网格，如图3 所示。总网格数约为8 000 个。弹性件为超弹性材料，采用C3D8H 单元；增强件为超强结构钢，采用C3D8R 单元；前、后法兰也是超强结构钢，采用C3D8R 单元；摆杆为刚性体，采用刚体约束条件。

图3 柔性接头网格模型Fig.3 Structured mesh of flexible joint

1.2 材料属性

柔性接头的弹性件具有高延伸率与低模量的特点，是几何与材料双重非线性，属于超弹性材料，采用超弹性模型较为合适。“三阶五项式”模型拟合弹性件的本构模型具有很高精度，文献[18]证明了在大应变范围内模型精度较高，即三阶Mooney-Rivlin 模型的变形，其应变能函数的表达式如下：

式（1）中：W是应变能；J1、J2是Cauchy-Green 应变张量的第一、二主不变量。

采用橡胶材料的单轴拉伸、平面剪切试验数据，拟合得到式（1）中的材料常数，如表1[9]所示。

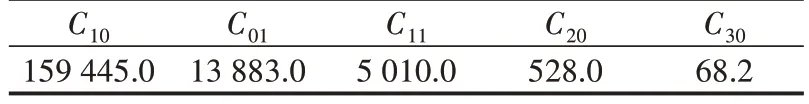
表1 三阶模型的材料常数Tab.1 Material constants for the third-order Mooney-Rivlin model单位：Pa

1.3 边界条件

柔性接头边界条件设置如图4所示。对称面采用对称约束条件，法线位移为0；后法兰采用固定边界条件；摆心具有平面内平动自由度U1、U2，绕法线转动自由度U6。

图4 计算模型边界条件Fig.4 Boundary conditions of model

柔性接头在地面试验时，承受载荷有燃烧室压力、喷射载荷与作动筒驱动载荷。柔性接头在工作时，燃烧室压力保持不变，作动筒驱动载荷大小与方向随柔性接头转动而改变。为了便于设定边界条件，作动筒驱动载荷采用刚性摆杆的转动实现，刚性摆杆与前法兰连接，燃烧室压力与喷射载荷采用等效的容器压力模拟。

2 数值验证

为确定本文方法的可靠性与精度，采用文献[13]柔性接头几何模型，应用本文数值计算方法，分别计算了在压力为1 MPa、2 MPa、3 MPa、4 MPa、5 MPa 与6 MPa 下柔性接头的轴向压缩变形，并与文献[13]实验数据进行比较，结果如图5所示。可知，本文方法计算结果的误差很小，计算方法是可靠的。

图5 在不同压力下数值计算与试验的轴向变形Fig.5 Axial deformation of numerical simulation and test under different pressures

3 计算结果与分析

3.1 压力载荷

采用本文数值方法，获取了在容器压力6 MPa 载荷下柔性接头的应力与变形分布。

在图1 中球坐标系下：图6～8 分别给出了弹性件剪切应力τ13、τ12、τ23分布情况。

图6 在容器压力6 MPa下弹性件剪切应力τ13分布Fig.6 Distribution of shear stress τ13 for elastomeric shims at vessel pressure of 6 MPa

图7 在容器压力6 MPa下弹性件剪切应力τ12分布Fig.7 Distribution of shear stress τ12 for elastomeric shims at vessel pressure of 6 MPa

表2 给出了弹性件剪切应力极值。可知，在容器压力6 MPa 下，弹性件剪切应力τ13比剪切应力τ12与τ23明显高。因此，弹性件剪切应力τ13为主要应力分量，其是弹性件重点关注的指标。

表2 在容器压力6 MPa下弹性件剪切应力极值Tab.2 Extreme value of shear stress for elastomeric shims at vessel pressure 6 MPa

在图1 中球坐标系下：图9～11 分别给出了增强件正应力σ11、σ22、σ33分布情况。

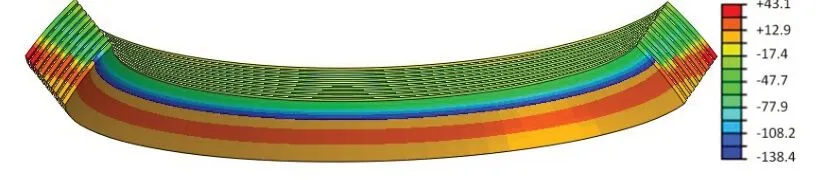
图9 在容器压力6 MPa下增强件σ11应力分布Fig.9 Distribution of normal stress σ11 for shims at vessel pressure of 6 MPa

图10 在压力6 MPa下增强件σ22应力分布Fig.10 Distribution of normal stress σ22 for shims at vessel pressure of 6 MPa

图11 在容器压力6 MPa下增强件σ33应力分布Fig.11 Distribution of normal stress σ33 for shims at vessel pressure of 6 MPa

表3 给出了增强件正应力极值。可知，在容器压力6 MPa 下，增强件正应力σ22为最大应力分量，应力极值为192 MPa，处于增强件内径处，是压应力。因此，增强件环向正应力σ22是增强件重点关注的指标。

表3 在容器压力6 MPa压力下增强件正应力极值Tab.3 Extreme value of normal stress for pads at vessel pressure of 6 MPa

为了分析柔性接头在容器压力下的变形，图12获取了在容器压力6 MPa 下，柔性接头最大位移为3.89 mm，位移前法兰中心处。

图12 在容器压力6 MPa下柔性接头位移分布Fig.12 Distribution of displacement for flexible joint at vessel pressure of 6 MPa

3.2 摆动载荷

采用本文数值方法，获取了在摆动角度6°下柔性接头的应力与变形分布。在图1 中球坐标系下：图13～15 分别给出了弹性件剪切应力τ13、τ12、τ23分布情况。

图13 在摆动角度6°下弹性件剪切应力τ13分布Fig.13 Distribution of shear stress τ13 for elastomeric shims at a defection angle of 6°

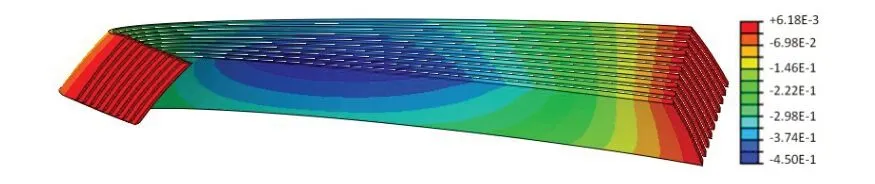
图14 在摆动角度6°下弹性件剪切应力τ12分布Fig.14 Distribution of shear stress τ12 for elastomeric shims at a defection angle of 6°

图15 在摆动角度6°下弹性件剪切应力τ23分布Fig.15 Distribution of shear stress τ23 for elastomeric shims at a defection angle of 6°

表4 给出了弹性件剪切应力极值。可知，在摆动角度6°下，弹性件剪切应力τ13比剪切应力τ12与τ23明显高，因此，弹性件剪切应力τ13为主要应力分量，是弹性件重点关注的指标。

表4 在摆动角度6°下弹性件应力极值Tab.4 Extreme value of stress for elastomeric shims at a deflection angle of 6°

在图1 中球坐标系下：图16～18 分别给出了增强件正应力σ11、σ22、σ33分布情况；表5 给出了增强件正应力极值。可知，在摆动角度6°下，增强件环向正应力σ22为最大应力分量，应力极值为13.9 MPa，因此，增强件环向正应力σ22是增强件重点关注的指标。

表5 在摆动角度6°下增强件应力极值Tab.5 Extreme value of stress for pads at a deflection angle of 6°

图16 在摆动角度6°下增强件σ11应力分布Fig.16 Distribution of normal stress σ11 for pads at a defection angle of 6°

图17 在摆动角度6°下增强件σ22应力分布Fig.17 Distribution of normal stress σ22 for pads at a defection angle of 6°

图18 在摆动角度6°下增强件σ33应力分布Fig.18 Distribution of normal stress σ33 for pads at a defection angle of 6°

为了分析柔性接头在摆动载荷下的变形，图19获取了在摆动角度6°下，柔性接头最大位移为26.2 mm，位移前法兰外侧处。

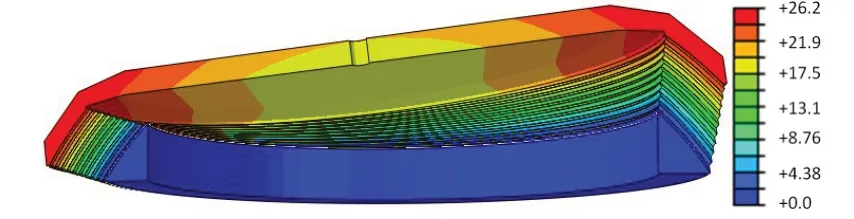
图19 在摆动角度6°下柔性接头位移分布Fig.19 Distribution of displacement for flexible joint at a defection angle of 6°

3.3 联合载荷

柔性接头在发动机工作条件下，同时承受压力与摆动载荷。为了验证柔性接头的结构安全性，需要获取柔性接头在容器压力为6 MPa 与摆动角度为6°联合载荷下的受力情况。由上文分析可知，在容器压力或者摆动载荷下，弹性件主要指标为剪切应力τ13，增强件主要指标为环向正应力σ22。图20给出了联合载荷下，弹性件剪切应力τ13分布，可知剪切应力最大值0.81 MPa，最小值0.66 MPa，满足文献[19]中的剪切强度小于4.2 MPa要求。

图20 在容器压力6 MPa与摆动角度6°下弹性件τ13剪切应力分布Fig.20 Distribution of shear stress τ13 for elastomeric shims under vessel pressure of 6 MPa and a deflection angle of 6°

图21 给出了联合载荷下，增强件正应力σ22。可知环向正应力最大值为316 MPa，为增强件外径处受拉；最小值为411 MPa，为增强件内径处受压。

柔性接头弹性比力矩特性对摆动喷管工作特性具有重要影响。图22给出了在不同容器压力下，弹性比力矩随摆动角度变化情况，可知，在一定的容器压力下，弹性比力矩随摆动角度增大而增大。

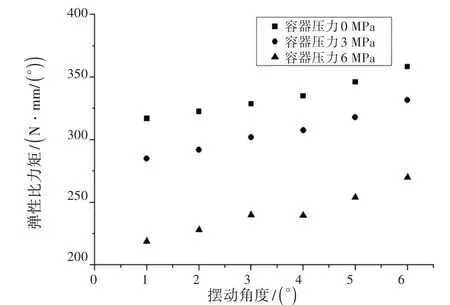
图22 在不同容器压力下弹性比力矩随摆动角度变化Fig.22 Spring ratio torque varies with the deflection angle under different vessel pressures

图23给出了在不同摆动角度下，弹性比力矩随容器压力变化情况。可知，在固定摆动角度下，弹性比力矩随燃气压力增大而减小。

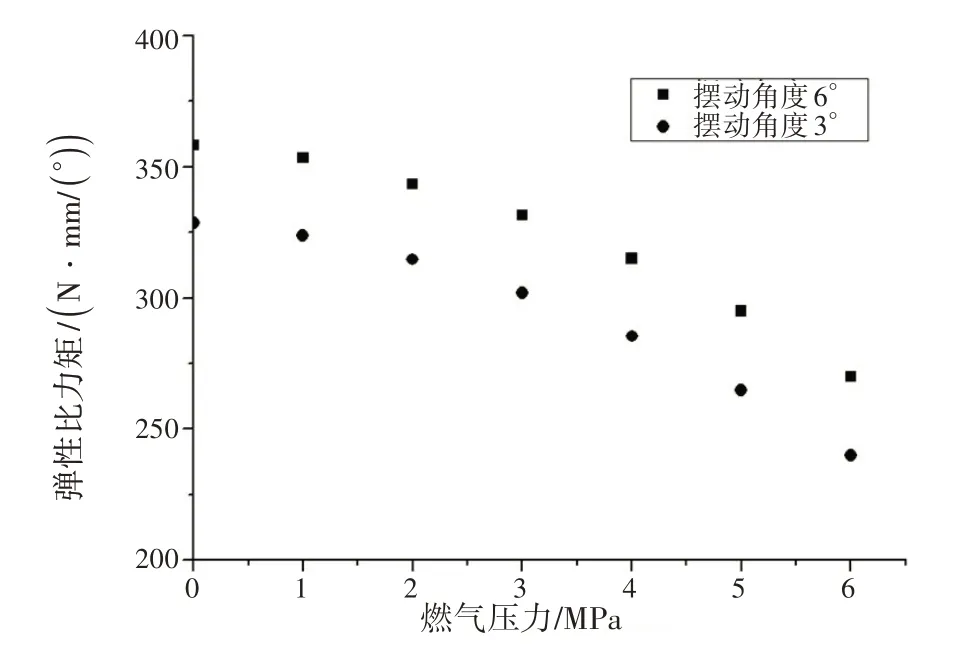
图23 在不同摆动角度下弹性比力矩随容器压力变化Fig.23 Spring ratio torque varies with the vessel pressure under different deflection angles

4 结论

本文建立了1 种刚体-柔性体结合有限元方法，研究了后摆心潜入式喷管柔性接头力学特性的数值仿真问题。计算与分析弹性件剪切应力分布规律、增强件正应力分布规律、柔性接头弹性比力矩分布规律，得出如下结论：

1） 柔性接头弹性件剪切应力主要分量为τ13，柔性接头增强件正应力主要分量为σ22；

2） 随燃气压力增大，柔性接头弹性比力矩降低；

3） 随摆角增大，柔性接头弹性比力矩增大。

通过本文的数值方法，评估了柔性接头弹性件与增强件的强度安全，为柔性接头工程设计提供了理论指导。