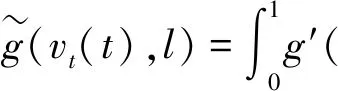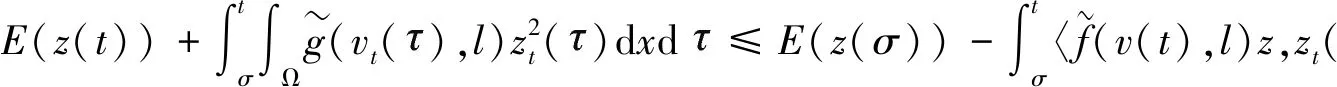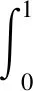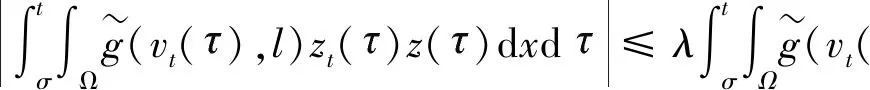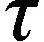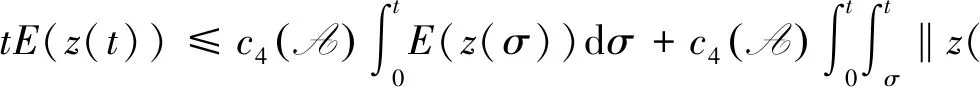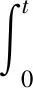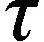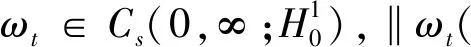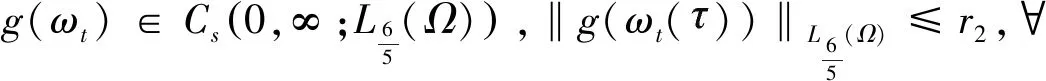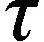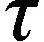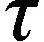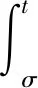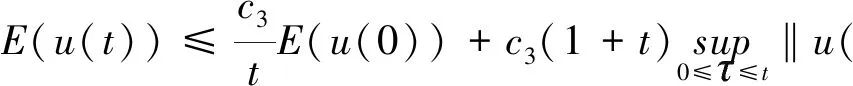具临界指数的非线性阻尼梁方程的全局吸引子

王思博,姜金平,王雪

(延安大学数学与计算机科学学院, 陕西 延安 716000)

0 引言

设Ω⊂3,我们考虑方程:

(1)

其中,h∈L2(Ω),g(ωt)为非线性阻尼项,f(ω)为非线性函数,α>0是粘性阻尼系数。

基于以上研究,文献[4-6]中研究了非线性梁方程的全局吸引子,马巧珍等[7-8]研究了基尔霍夫型梁方程的全局吸引子和具有记忆项的拉回吸引子,同时苏小虎,姜金平[9]讨论了时间依赖全局吸引子的存在性,但是目前研究具有临界指数的全局吸引子文献相对较少,孟凤娟,曹凤雪[10]研究了具临界指数的波方程的时间依赖全局吸引子。本文中讨论具临界指数的非线性阻尼梁方程的全局吸引子。利用文献[11-13]中的思想,证明了在条件式(2)～(5)下问题(1)的全局吸引子的存在性,并改进了文献[4]中的结果。此外,在附加条件式(30)下我们证明了全局吸引子的正则性和有限分形维数,并改进了之前的结果。

1 预备知识

我们令H=L2(Ω),在H中的内积和范数分别用〈·,·〉和‖·‖来表示.我们也用‖·‖1来表示在下面H1中的范数。

非线性项f和g满足下列条件

f∈C1(),|f′(s)|≤c(1+|s|2)

(2)

(3)

g∈C1(),g(0)=0,g是严格单调递增的。

(4)

|g(s)|≤c(1+|s|5)

(5)

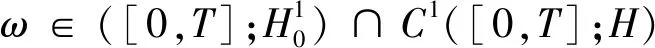
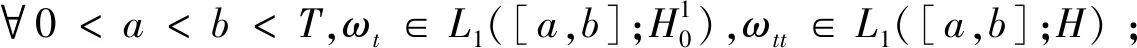
ii)对于所有t∈[0,T],αΔ2ω+g(ωt)∈H;

iii)对于所有t∈[0,T],且x∈Ω使得方程(1)成立,

则ω称为问题(1)在[0,T]×Ω上的强解。

则称ω为问题(1)在[0,T]×Ω上的广义(弱)解。

关于问题(1)解的适定性在文献[14]中已经得到证明,这里不再进行论证。

(6)

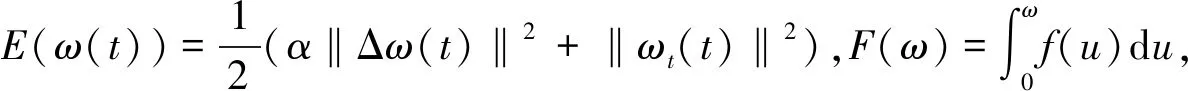
2 全局吸引子

定义2.1[15]设{S(t)}t≥0是度量空间(X,d)上的半群.一个最小的,非空的有界闭集A⊂X满足:

对于每一个有界集合B⊂X,称为{S(t)}t≥0的全局吸引子。

在(6)式中考虑条件(2)～(5),我们可以给问题(1)插入一个不递增的李亚普诺夫函数

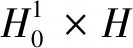
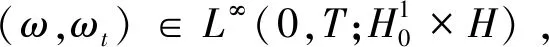
F(ω)∈C([0,T];L1(Ω)),

并且

(7)

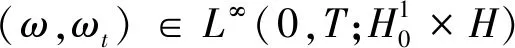
则有

在空间L1((0,T)×Ω)上F(ωn)→F(ω)强收敛;

则(2.1)式成立。

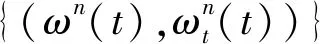
(8)

(9)

则由紧嵌入定理可得

在空间C([s,T];H)中,ωn→ω强收敛

(10)

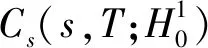
则根据嵌入定理可得在空间L1(Ω)中F(ωn(t))→F(ω(t))强收敛,∀t∈[s,T]。

由引理2.1可得

=0.

(11)

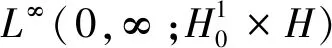
(12)

(13)

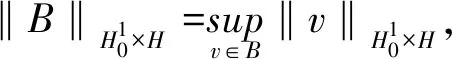
(14)

≤E(ωn(s)-ωm(s))

(15)

则

由文献[13]可知∀δ>0,∃c2(δ)>0,使得

|u-v|2≤δ+c2(δ)(g(u)-g(v))(u-v)∀u,v∈R。

通过以上两个不等式,我们有

(16)

对于每个δ>0,将下式

两边同时乘以ωn-ωm,然后在[0,T]×Ω上积分,并且根据式(13)可得

(17)

由式(16)和式(17)可得

对式(15)关于s在[0.T]上积分,并根据上面的不等式可得

(18)

则由引理2.2可得

(19)

另一方面,由于

由文献[18,定理5.1],可得

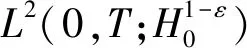
则有

(20)

现在对K4进行估计,使用Hölder不等式有

(21)

利用文献[12]相似的技巧,通过式(5)和式(12)可以得出

+TmesΩ(|g(-δ)|+|g(δ)|)

(22)

由式(21)～(22)可得

(23)

因此由式(18)～(20)和式(23)可得

则

又因为g∈C()且g(0)=0,则不等式(11)成立。

下面证明半群{S(t)}t≥0的渐近紧性。

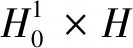
3 吸引子的正则性和有限维数

根据文献[19]可得,A是不变的,对于每一个φ∈A存在一个不变的轨迹γ={W(t),t∈R}⊂A,使得

W(0)=φ

(24)

其中不变的轨迹是指连续曲线γ={W(t),t∈R},这使得

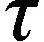
证明全局吸引子A的正则性和有限维数,需要以下引理:

引理3.1假设K是H1上的一个相对紧的子集,并且f(·)满足条件(2),则对于任意的ε>0,存在δ>0,使得‖u2-u1‖1<δ,

‖f′(u2)-f′(u1)‖L3(Ω)≤ε,∀u2,u1∈K

(25)

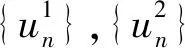
(26)

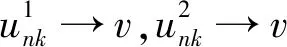
则有

(27)

另一方面,由式(26)和式(2)可以推出:

则式(27)成立。

=0.

与式(26)中第3个关系式矛盾,引理3.1得证。

引理3.2假设K是H1的一个相对紧的子集,并且f(·)满足条件(2),那么对于∀ε>0,∃c(ε)>0,使得

‖f′(v)u‖≤ε‖u‖1+c(ε)‖u‖,∀v∈K,∀u∈H1

(28)

对于每一个v∈K,利用引理3.1,可得

则有

(29)

所以

再由式(29)可得式(28)成立。

下面证明全局吸引子的正则性。

定理3.1令条件式(2)～(5)成立,假设

(30)

则∃R>0,使得

‖φ1‖1+‖φ2‖1+‖Δφ1+g(φ2)‖≤R,φ=(φ1,φ2)∈A.

定理3.1的证明设φ=(φ1,φ2)∈A且γ={W(t),t∈R}⊂A是一个满足式(24)的不变轨迹,由不变轨迹的定义可以得出

W(·)=(ω(·),ωt(·)),

(ω(t+s),ωt(t+s))=S(t)(ω(s),ωt(s)),∀t≥0,∀s∈R.

那么v(t)=ω(t+s)是下面问题式(31)的解,

(31)

设s<0,且0

(32)

则

z0=ω(s+l)-ω(s),z1=ωt(s+l)-ωt(s).

将式(32)第一个式子两边同时乘以zt和z,并且在(σ,t)×Ω上积分可得:

(33)

(34)

另一方面,由式(30)可得

与(33)式联立可得

(35)

(36)

由式(33)～(36)可得

(37)

其中0≤σ≤t。

对于μ∈(0,1),我们用强解来证明它,因为式(37)是式(31)的强解,所以作为广义解也是正确的,因为它们可以用一系列强解来逼近。

(38)

选择足够小的ε,结合式(37)和式(38)可得

(39)

在式(39)上关于σ在[0,t]上积分,可得

(40)

另一方面,由于(ω(s),ωt(s))∈A,∀s∈R,由式(6)和式(30)可得

则

将上面的不等式代入式(40)可得

tE(z(t))≤cE(z(0))+cl2(1+t),∀t≥0

(41)

当s→-∞时,有

(42)

由不等式(42)与ωt∈C([0,∞];H)可得

(43)

并因此有

(44)

(45)

其中,r3与ω(t)无关,在式(31)的第一个式子下,利用式(43)～(45)可得

(46)

其中,r4与ω(t)无关,因此,对于每一个φ=(φ1,φ2)∈A,有

‖φ1‖1+‖φ2‖1+‖Δφ1+g(φ2)‖≤R.

其中R不依赖于φ.

下面证明A的有限维数.

定理3.2假设满足定理3.1中条件式(30),那么全局吸引子A的分形维数是有限的.

定理3.2的证明设φ1=(ω0,ω1)∈A,φ2=(v0,v1)∈A,(ω,ωt)=S(t)φ1,(v,vt)=S(t)φ2,并且令u=ω-v,则u(t,x)是下面问题的解

(47)

给式(47)第一个式子两边同时乘以ut和u,并且在(σ,t)×Ω上积分可得

(48)

则

(49)

在定理3.1中提到,我们可以利用稠密性来证明式(48)和式(49),利用Gronwall引理,从式(48)中可得

(50)

其中,常数c1和ω依赖于A,但是不依赖于φi(i=1,2)。

另一方面,利用式(48)～(49)和引理3.2,并且运用定理3.1中的论证,可得

对于上述不等式关于s在[0,t]上积分可得

(51)

其中,c3依赖于A,但不依赖于φi(i=1,2)。

因此,根据文献[11,定理3.11]和式(50)～(51)可以得出A的分形维数是有限的。