小波分析在锚杆无损检测中的应用

任长安

（河北省水利水电勘测设计研究院集团有限公司，天津 300220）

锚杆是各类工程支护的重要组成部分，作为深入地层的受拉构件，它一端与工程构筑物连接，另一端深入地层中，整根锚杆分为自由段和锚固段。传统检测方法为空心液压千斤顶拉拔法等破坏性检测方法，受场地等因素制约很大，浪费人力物力。基于这种情况，随着技术发展，锚杆的无损检测方法应运而生，具有无损、高效等优点，此后得到大量运用。锚杆无损检测主要是检测施工后锚杆的杆体长度和锚固段灌浆密实度，其理论基础是冲击弹性波法。通过分析采集后的波形信号，得到锚杆的长度范围及缺陷位置。

锚杆无损检测过程中易被外界和仪器本身的噪声干扰， 导致所得信号失真， 无法准确判断所得结果。所以对原始信号的消噪处理就显得格外重要。传统的处理方法有很多， 使用较多的方法为傅立叶分析，傅立叶变换建立了时间域和频率域的联系，可有效获得信号的频率构成， 通过滤波过滤掉噪声所在的频率信号，对信号重构后可有效去除噪声影响，达到消噪滤波的目的。但傅立叶分析的缺点很明显，它只能对信号进行整体分析， 而无法对局部信号进行处理，导致某些有用信号被过滤掉。因此在20 世纪80 年代，小波分析方法被提出，同样是一种时频交互分析方法， 通过伸缩平移运算对信号进行多尺度的分析，在时域和频域同时具有良好的局部化特性，常被誉为信号分析的“数学显微镜”［1］，在许多领域得到广泛运用。 所以尝试在锚杆检测的信号分析中引入小波分析，以达到去除噪声的目的。

1 小波分析原理

小波分析方法是一种窗口面积固定但其形状可改，时间窗和频率窗都可改的时频局域化分析方法，即在低频部分具有较高的频率分辨率和较低的时间分辨率， 在高频部分具有较高的时间分辨率和较低的频率分辨率。

小波变换的含义： 把一称为基本小波的函数Ψ(t)做位移τ 后，再在不同尺度a 下与待分析信号x(t)做内积：

等效的频域表示为：

式中X(ω)，Ψ(ω)分别为x(t)，Ψ(t)的傅立叶变换。

在实际工程中，需要低频信号，噪声一般是高频信号，小波消噪的基本流程：首先选择合适的小波信号，对实测信号进行多尺度分解，具体过程是：第一层可将信号分为低频和高频两个子带， 第二层将第一层得到的低频子带再次分解成低频和高频两个二级子带，以此类推。从而得到信号的各级子带，因为工程信号噪声一般存在于高频信号中， 所以通过对高频子带的处理，以过滤噪声信号，然后对各级子带进行重构， 得到去除噪声的重构信号， 达到滤波目的。三层分解过程如图1。

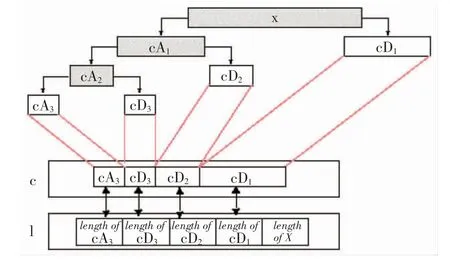
图1 三层小波分析示意图

2 锚杆信号的采集

当工程的结构构件的尺寸为圆柱体且其直径d远小于其长度L 时，即L>d，则此构件完全可以作为弹性波中的一维杆件理论分析处理。 锚杆是钢筋与混凝土胶结在一起，与周围围岩（土）存在较大的弹性波波阻抗差异，因此，应用弹性波理论对锚杆进行无损检测，可以视锚杆为一维弹性杆件［2］，用一维弹性杆件来检测分析锚杆的质量， 即钢筋与混凝土的胶结质量、混凝土与围岩（土）的胶结质量（也就是锚杆的饱满度）及锚杆的长度。

当锚杆锚固体系存在波阻抗（Z=ρVA）差异的界面时（如空浆、欠密实、欠长度等），弹性波在该界面将发生反射。根据检测到的反射信号的频率、幅值及反射波的时间等特征， 可确定锚杆的锚固状态及施工缺陷。

锚杆锚固质量检测采用的方法为应力反射波法。其基本过程：在锚杆端部激发应力波，应力波沿锚杆向下传播， 遇到波阻抗发生变化的界面产生反射波，安装在锚杆端部的探头接收到此反射波，通过分析此反射波的性质来推断锚杆的长度和空浆、欠密实等缺陷。

3 锚杆实测信号的处理

3.1 小波函数选择

小波分析中所用到的小波函数具有不唯一性，即有多种小波函数可选择。 所以选择合适的小波函数是关键问题。基于锚杆信号噪声高频的特征，所以选择的小波函数应该具有优秀的时频局部化特点［3］，Daubechier(dbN)小波符合这一要求，选择这个小波作为小波母函数。

3.2 实测信号的小波系数提取

本次实测信号通过武汉中岩科技股份有限公司生产的RSM-RBT(C)型号锚杆无损检测仪采集，仪器采样间隔1～1000 μs，采样长度最高可达8 K，采集器带宽2～50000 Hz。

在锚杆无损检测中，噪声信号一般出现在小波变换的小尺度当中， 分离出的信息数据一般没有规则，并且当尺度增加后， 对应位置的能量会迅速减小；而有用信号的能量不会随着尺度增加出现明显变化，且信号的正负基本一致。根据这些特征，就可通过小波变换把噪声与有用信号区别出来，从而去除噪声［4］。

本次测试的原始波形如图2。

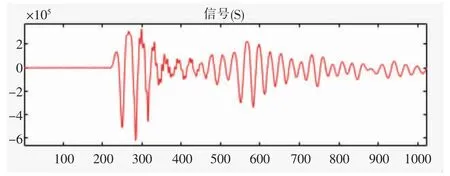
图2 锚杆原始波形

针对原始信号，使用Matlab 软件实现小波分解，选择上文选出的DB3 小波基，对信号进行4 层分解，分解结果如图3。

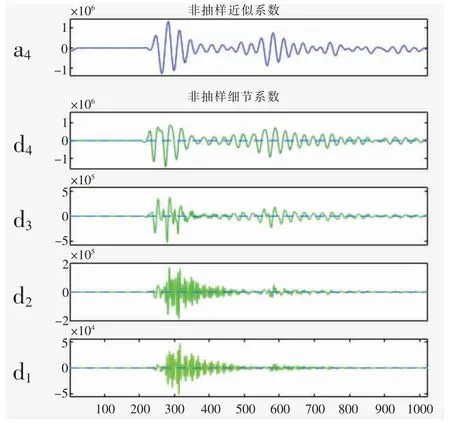
图3 各级小波分解

如图3，d1～d4是小波分析的4 级高频信息，a4是最后分离出来的低频信号。 可以看出，d1～d3的数据几乎没有相关性， 且其绝对值较小， 且随着尺度增加，能量出现很大衰减，所以认为锚杆数据的噪声集中在此。 而对检测有用的缺陷信号应该集中在d4和a4中。于是在软件中把d1～d3这3 级小波分解参数置零，同时把d4小于阈值的置零，然后对信号进行重构就得到滤除噪声后的信号，如图4。

图4 去噪重构后波形

观察图4 去噪重构后的波形， 可看到重构波形相比原始波形，高频毛刺噪声明显降低，这是由于重构波形基本只包含了有用信号，噪声被滤除，信号的缺陷判断能力得到增强， 比直接使用原始信号更加可靠。

分析重构后波形图，可看出波形较规则，信号呈平缓衰减状态，无缺陷反应，故判断该锚杆注浆饱满度良好。

4 结语

（1）小波分析是当前数学和工程学科中快速成熟的一个新方向，经过几十年的发展已相当成熟，其理论基础和应用经过无数的应用和验证， 被证明是可行完备的。它实际是时频的一种转换方法，但可完成局部的信号分析提取，尺度可自由调整，小波母函数众多，可适应各种信号分析的需求，相比傅立叶变换拥有更多优点［5］。

（2）锚杆检测信号中的噪声为高频信息，这就要求对于噪声信息的研究，其时间间隔应越小越好，这样就可准确分析出高频噪声所处的位置， 从而精确消噪；而有用信息是低频信号，研究其时间间隔应该相对加大，以满足获取至少一个周期的完整信息。小波变换的特点完美符合这一要求， 在大幅度保留有用信号的前提下，对于信号的消噪效果优秀。

（3）matlab 软件作为专业的数学分析软件，拥有强大的信号处理分析能力，在其工作环境下，可方便地进行信号识别、小波分析、信号分解及重构等。