基于多特征融合的高机动多目标低截获概率跟踪技术
2024-03-07周建江
陈 军 丁 一 王 杰 汪 飞 周建江
(1.南京信息工程大学电子与信息工程学院,江苏南京 210044;2.南京航空航天大学雷达成像与微波光子技术教育部重点实验室,江苏南京 210016)
1 引言
现代战争中,雷达在进行目标探测与跟踪时,其辐射信号极易被敌方接收机截获,从而严重威胁雷达的战场生存能力,所以低截获概率已成为雷达必不可少的性能之一[1]。雷达只有具备低截获概率性能,才能在激烈的电子战中生存下来,并发挥其该有的战术和技术性能[2]。因此,对雷达低截获概率性能的研究已然成为现代雷达研究的热点问题之一,不断吸引着越来越多的学者研究。
常见的雷达低截获概率实现方法包括低截获概率波形设计、低副瓣天线设计和低辐射能量控制。其中,低辐射能量控制是实现雷达低截获概率性能最直接有效的方法。对于雷达低辐射能量控制,国内外已经取得了较为丰富的研究成果。文献[3]通过搜索和跟踪状态的功率控制,实现了雷达的低截获概率探测技术。文献[4]利用模糊变量表征法研究了机会阵雷达的功率分配问题。文献[5]提出一种低截获背景下的快速功率分配算法。然而,现有的大部分低辐射能量控制方法都是针对常规目标的,少有针对高机动目标的研究。本文重点针对高机动多目标的雷达低辐射时间控制展开研究,在确保高机动多目标跟踪精度的前提下减少雷达辐射次数。
在高机动目标跟踪方面,文献[6]提出一种基于多项式滤波器的复合扩展记忆多项式/衰落记忆多项式滤波算法,提升机动目标跟踪精度。文献[7]提出一种基于自适应协同容积卡尔曼滤波的分布式估计方法,通过添加时变衰落因子设计自适应容积卡尔曼滤波器来实时调整滤波增益矩阵,进而提升跟踪精度。但上述算法均未从根本上解决因状态转移矩阵与当前运动模型不匹配导致的低跟踪精度问题,本文对于针对这一问题通过实现目标机动时运动状态模型自适应更新来提升目标跟踪精度。在多目标跟踪方面,概率数据关联(Joint probabilistic data association,JPDA)[8]和随机有限集算法(Random finite set,RFS)[9-11]是两种常用的数据关联算法,其中JPDA 对中等数量的目标跟踪具有良好的性能,而RFS 可以处理目标的生成和消亡,因此对处理数量不确定的目标跟踪上有着良好的优势。由于本文研究当前目标跟踪数下的低截获概率跟踪技术,目标的产生和消亡对本文研究算法没有影响,因此,本文基于JPDA 算法研究高机动目标低截获概率跟踪技术的基本原理。
在高机动多目标的跟踪过程中,本文基于目标轨迹聚类算法实现目标运动状态模型的自适应更新。在目标轨迹聚类技术方面,DBSCAN(Densitybased spatial clustering of applications with noise)算法是一种基于密度聚类的算法[12]。相较于其他传统轨迹聚类算法,DBSCAN 算法具有能处理不规则数据图形、抗噪声能力强的优点。对于DBSCAN算法的改良和应用,国内外也取得了较为丰富的研究成果。文献[13]提出一种基于层次的DBSCAN 改良算法HDBSCAN(Hierarchical density-based spatial clustering of applications with noise)。文献[14]提出了一种基于启发式迭代的DBSCAN聚类算法。文献[15]提出了一种基于粗糙集改进的DBSCAN。上述三种改良算法中,HDBSCAN 算法结合了层次聚类算法和密度聚类算法的优点,在抗干扰性强的前提下降低了算法的复杂度,适用于本文杂波环境下的聚类。但常见的DBSCAN 改良算法均使用单一特征值进行聚类,对具有相似运动模式的高机动目标无法准确的判断。针对这一问题,文献[16]将Mean-Shift 聚类算法与轨迹多特征结合,提出一种基于多特征信息融合的目标轨迹聚类方法,提高对具有相似运动模式的高机动目标聚类精度。
本文将多特征信息融合的目标聚类方法与HDBSCAN 聚类算法相结合,提出一种多特征融合的轨迹聚类算法,通过将四种轨迹特征独立HDBSCAN 聚类的结果进行融合,提升聚类精度。接着,本文基于多特征融合的轨迹聚类算法提出一种基于运动状态模型自适应更新的高机动多目标跟踪算法。该算法可以根据波动参数自适应更新状态转移矩阵,从而提升多目标跟踪算法的跟踪精度,解决了传统多目标跟踪算法因状态转移矩阵固定而导致的低精度问题。为了进一步提升跟踪精度,本文在无源传感器跟踪的基础上引入雷达间歇辐射,提出一种基于轨迹聚类的多传感器协同管理算法。该算法可以根据本征堆积误差进行雷达辐射决策,从而在确保目标跟踪精度较高的前提下降低雷达辐射次数,提升低截获概率性能。
2 多特征融合的轨迹聚类算法
2.1 轨迹特征描述
机动目标的运动轨迹本质是其时间到空间上的一个映射,轨迹包含了目标在时间、空间领域及其本身属性的相关信息[17]。在某一特定环境下,通过对机动目标进行跟踪,可以得到一系列质心点,连接上述质心点便可以得到目标运动轨迹。假设二维空间上的坐标为(xk,yk),当前时间戳为tk,则目标轨迹可以表示为:
在一个机动目标的运动过程中,当轨迹模型改变时,其不同帧间的轨迹并不相同,而机动目标特定模型的空间轨迹分布都具有一定的特点,因此可以通过机动目标的帧间轨迹均值M作为一种位置轨迹特征,即,
对于轨迹角度信息,设置某一转角阈值。当目标轨迹转角超过阈值,则标记为对应特征点,根据特征点的分布情况,轨迹转角θk可以作为一种瞬时角度轨迹特征,如式(3)所示,
对于轨迹速度信息,可以将目标运动速度的大小作为目标特征依据。速度又分为瞬时速度vk与平均速度,分别用式(4)和式(5)表示:
其中,连续时间间隔都是相同的。当瞬时速度vk过高的时候,此时做转弯运动的概率较小;而平均速度vˉ过高的时候,整个过程中做直线运动的概率较大。
2.2 基于多特征融合的轨迹聚类算法
考虑到定位追踪高机动多目标对抗干扰性和灵活性的要求,本文采用HDBSCAN 算法。其基本思想是给定一个数据集X、任意对象a、R∊邻域和最少点数阈值MinPts,其中R∊邻域是指以a为圆心、以R∊为半径的圆形数据集区域。第一步进行聚类簇的划分,将数据集中的每个数据点看作一个对象,通过计算不同对象之间的欧式距离来确定其对应的R∊邻域,并通过R∊邻域的范围与MinPts 的比较划分出X中的噪声点、边界点和核心点,最后凭借X中核心点间连通性生成聚类簇。第二步进行基于层次的聚类簇组合,由于第一步的划分中存在核心点和边界点同时被划分到多个聚类簇中,即各簇之间存在公共点。将含有公共核心点的聚类簇组合成一个新的簇,而对于公共边界点则将其划分到与其欧氏距离最近的核心点对应的簇中。重复上述步骤,直到簇间不存在公共点,算法结束。
传统的HDBSCAN 聚类算法常常仅使用单一特征进行聚类,例如仅考虑相邻两帧之间的运动矢量。然而,单一特征只能反映轨迹的某一方面特征,若仅使用单一特征进行聚类,将无法准确判断具有相似运动模式的机动目标。
为了进一步提升模型匹配的精度,本文使用高机动目标的帧间轨迹均值M、轨迹转角θk、瞬时速度vk和平均速度vˉ四个空间特征作为特征,把不同特征相对应特征空间内所得的聚类结果进行关联,再将所得融合聚类结果与剩余未处理轨迹之间建立联系,最后得到轨迹的运动模型。由于本文所使用的多特征融合聚类是在每个单独特征空间聚类完成后进行,因此能够避免传统算法在聚类前融合引起的维数问题。多特征融合轨迹聚类方法流程如图1所示。

图1 多特征融合轨迹聚类方法流程图Fig.1 Flow chart of multi-feature fusion trajectory clustering method
假设特征空间样本集为D={F1,…,F4},将D中每个样本Fn进行单独的聚类,则四个样本空间分别得到不同的聚类数目{Ni|i=1,…,4}。进行融合聚类后,其聚类结果需要包含上述四个特征空间的所有聚类结果,因此在进行融合聚类后的聚类数目Nm为四个聚类数目中最大值,即Nm=max{N1,…,N4},其余特征空间缺少的聚类数目通过补零使得Ni=Nm。经过上述操作,单一特征空间的聚类结果为{|l=1,…,Nm}。
为了与剩余未处理轨迹进行关联,需要计算出每条轨迹与已有轨迹聚类之间的概率映射关系。假设尚未融合的轨迹为G,聚类结果的标准差为,均值为μl,m,则未融合轨迹G与未融合聚类结果之间的条件概率为:
对于未融合轨迹G与已融合聚类结果,聚类结果的标准差为,均值为ξa,m,G与之间的条件概率为
根据式(7)和式(8)的条件概率,可以对剩余轨迹的分配进行决策。当时,则认为G会与该已融合轨迹建立联系,即将G分配给该融合轨迹。否则,将该轨迹分配给最小的轨迹。当所有剩余的轨迹均已分配完毕,融合聚类算法结束,步骤如图2所示。
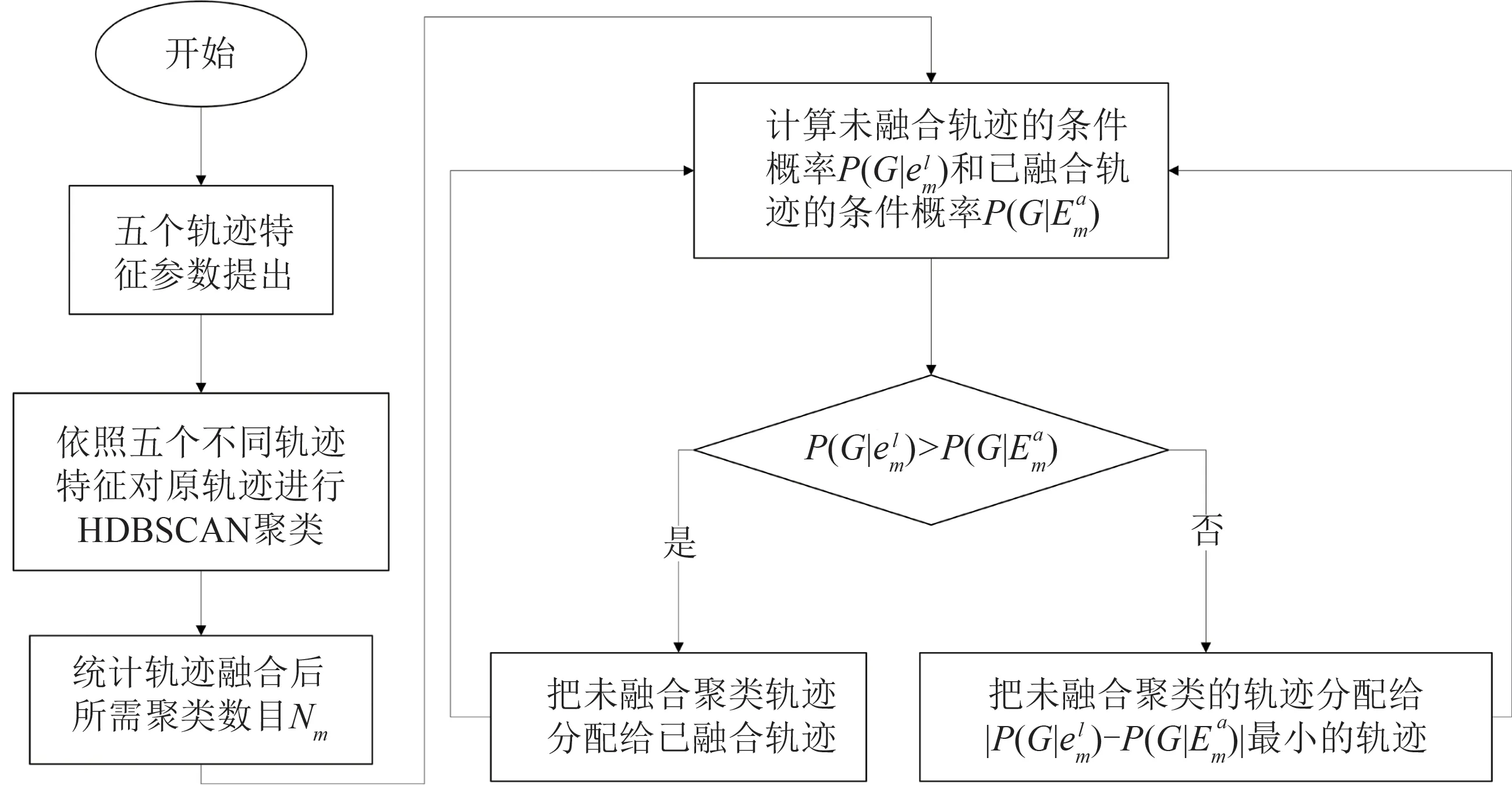
图2 基于多特征融合轨迹聚类算法流程图Fig.2 Flow chart of trajectory clustering algorithm based on multi-feature fusion
3 基于目标运动状态模型自适应更新的多目标跟踪算法
目标跟踪中最简单的情形是非杂波背景下的非机动单目标跟踪,但实际应用环境中常以机动多目标跟踪为主[18]。在多目标跟踪的问题中,由于多个目标以及杂波的干扰,传感器往往会同时获得多个测量,此时需要通过相应算法减少数据关联的个数,再通过滤波算法实现目标跟踪。这是一般的基于轨迹预测的多目标跟踪算法,但仍没有考虑到高机动目标跟踪问题。
针对这一问题,本节引入2.2 节所提出的基于多特征融合的轨迹聚类算法,在传统扩展卡尔曼滤波法(Extended Kalman filter,EKF)的基础上加以改进[19],提出一种基于目标运动状态模型自适应更新的高机动多目标跟踪算法(High maneuvering multiple targets-Extended Kalman filter,HMMΤ-EKF),其流程图如图3所示。
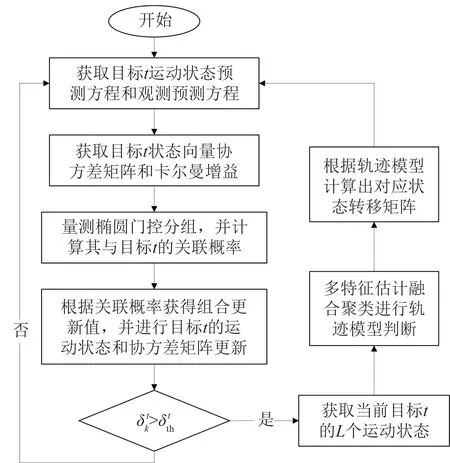
图3 基于目标运动状态模型自适应更新的多目标跟踪算法Fig.3 Multi-target tracking algorithm based on adaptive update of target motion state model
假设k时刻目标t运动状态为,目标状态向量的协方差矩阵为,量测噪声均值为0、方差为。非线性状态方程为f(x),非线性观测方程为h(x),则这两个非线性方程的雅克比矩阵和分别为
目标t运动状态预测方程为:
目标t的观测方程为:
目标t状态向量的协方差矩阵为:
滤波算法的卡尔曼增益为:
为了进行量测与多目标的匹配,本文选择JPDA 算法进行的数据关联。首先计算量测与目标之间的椭圆门控距离,得到满足跟踪门限要求的量测,即
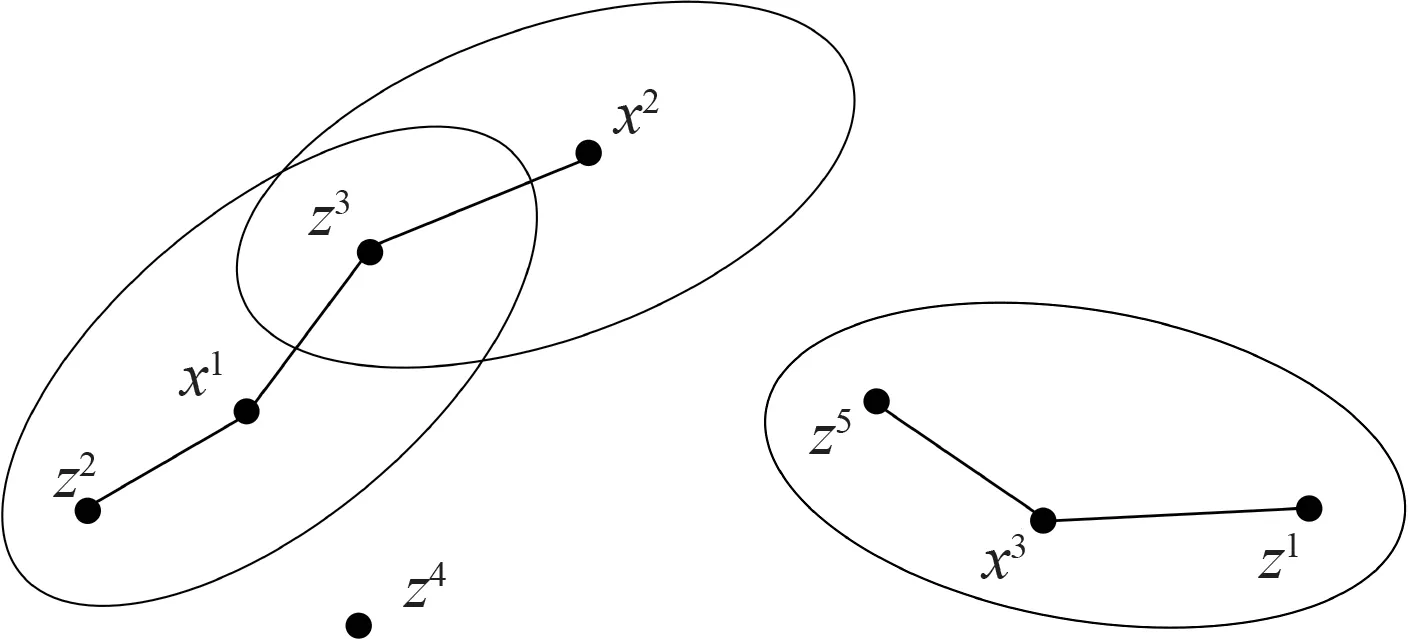
图4 椭圆门控分组Fig.4 Oval gated grouping
在图4中,有三个先验x1,x2,x3椭圆分别代表其门控,四个观测z1,z2,z3,z4,z5,其中z1,z2,z3,z5落在椭圆之内,则{x2,x1,z2,z3}为一组,{x3,z1,z5}为一组。
已知目标检测概率为PG,总轨迹条数为aτ,总量测数目为nc,总杂波数目为n0,错误量测密度为γ,目标检测指示器为δt,归一化常数为bt,j,两侧分配标志为τt,j,组合值为qk,则量测j与目标t在时间k时的关联概率为:
同时,k时刻目标t的更新协方差矩阵为:
状态转移矩阵由目标状态模型决定,根据传感器的量测值进行多状态融合的轨迹聚类可以估计目标运动状态。对于状态转移矩阵更新的决策,本文引入波动参数。
当目标t运动状态模型不变时,其相邻两个时间间隔内的较小;而当目标t运动状态模型转变时,由于状态转移矩阵不再适应当前的运动模型,较大。
其中,T表示当前采样周期。
同理,若目标t做协同拐弯运动,则状态转移矩阵通式为:
其中,ω表示当前目标运动角速度。
4 基于轨迹聚类的多传感器协同管理算法
作为有源传感器,雷达可以获取被跟踪目标的位置信息和角度信息。但雷达在进行多目标探测和跟踪时,其辐射信号极易被敌方接收机截获,不利于低截获概率跟踪[20]。无源传感器不会主动向外辐射信号,但其只能获取目标的角度信息,即使利用多站无源时差定位算法(Τime Difference of Arrival,ΤDOA)获取位置信息,其跟踪精度仍然不高。
针对上述问题,本小节提出一种基于轨迹聚类的多传感器协同管理算法。该算法使用无源传感器结合ΤDOA 算法获取目标的位置信息和角度信息作为HMMΤ-EKF 的观测值输入,在跟踪误差较大时使用雷达间歇辐射进行轨迹参数的修正,并使用基于多特征融合的轨迹聚类算法进行状态转移矩阵更新,在确保目标跟踪精度较高的前提下减少了雷达辐射次数,实现低截获概率跟踪。基于轨迹聚类的多传感器协同管理算法如图5所示。
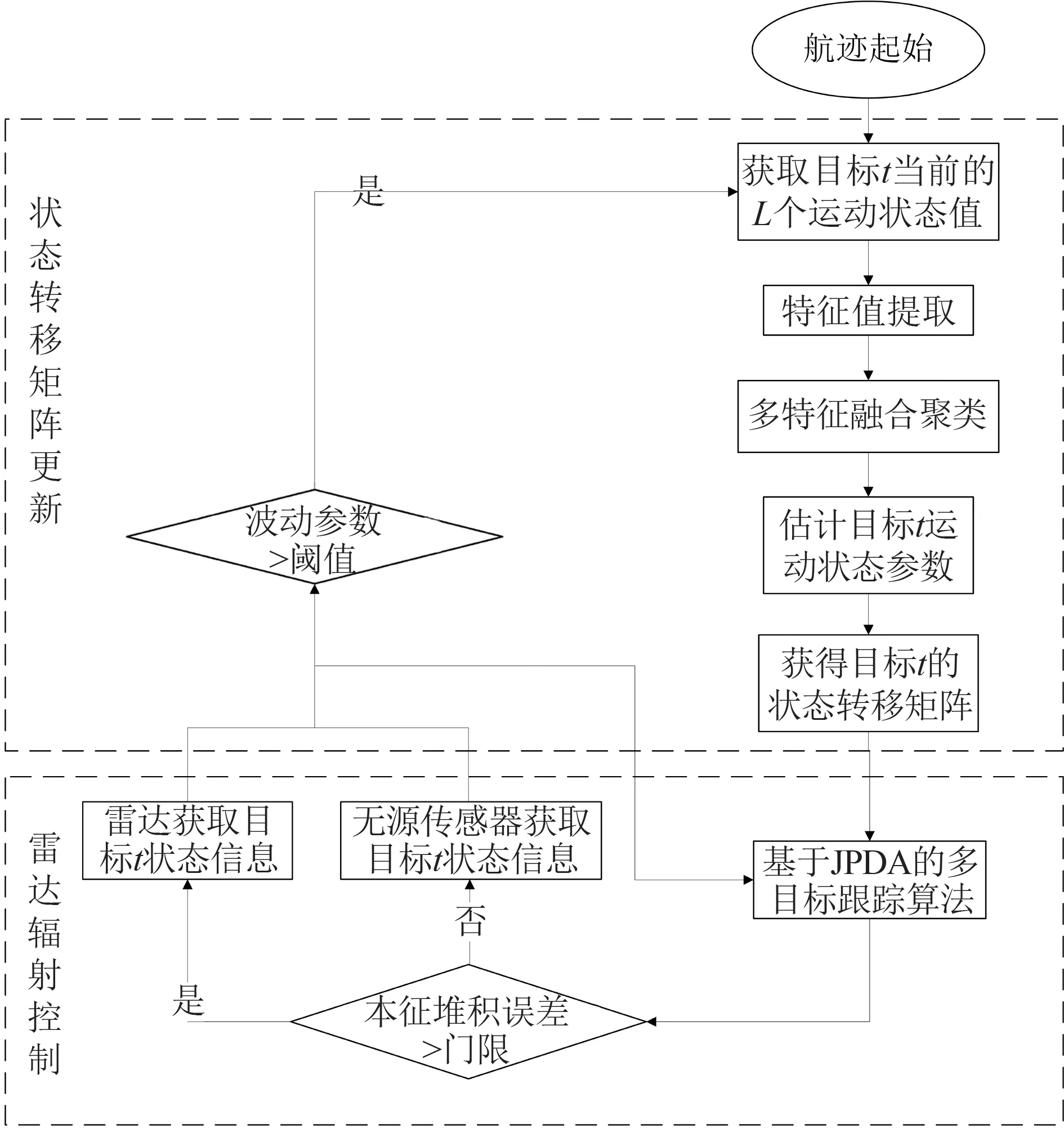
图5 基于轨迹聚类的多传感器协同管理算法Fig.5 Multi-sensor collaborative management algorithm based on trajectory clustering
其中,Η表示观测方程的噪声转移矩阵,Vk表示均值为0的高斯白噪声,j表示当前使用的传感器。
假设雷达为传感器组1,多站无源传感器为传感器组2,则当雷达作为观测传感器对目标t进行跟踪,即j=1时,观测值为:
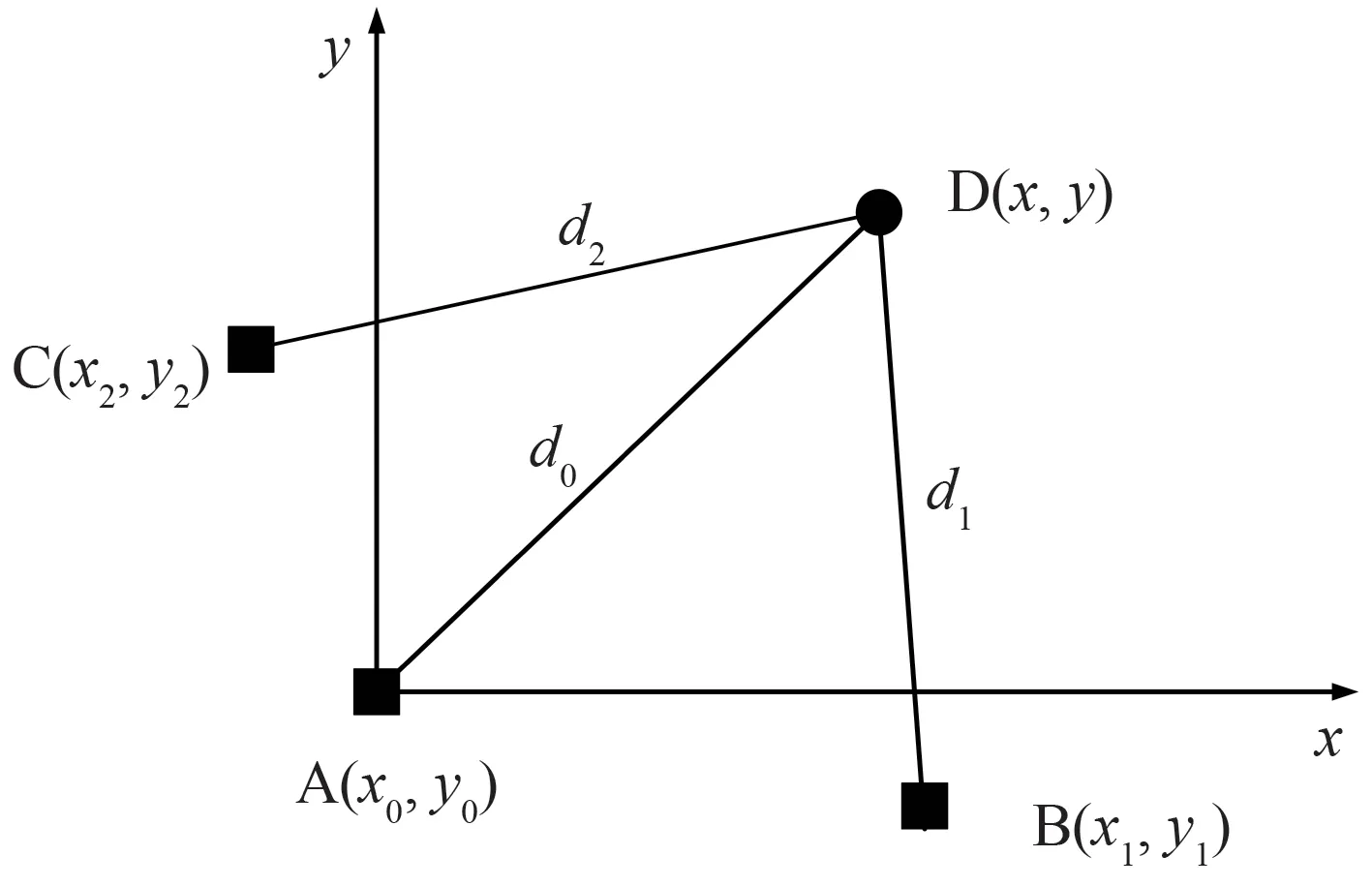
图6 三站时差定位模型图Fig.6 Τhree-station time-difference location model
在图6 中,点D 代表敌方辐射源,点A、B、C 代表对目标进行跟踪的三个无源传感器。假设在k时刻,敌方辐射源的坐标为D(x,y),三个无源传感器的位置坐标分别为A(x0,y0),B(x1,y1),C(x2,y2)。敌方辐射源到三个无源传感器的位置分别为d0,d1和d2,其与目标位置具有的数学关系如式(24),
假设无源传感器A 所在位置为主跟踪定位站,无源传感器B 和C 所在位置为辅助跟踪定位站,c表示电磁波在空气中的传播速度,信号到达各辅助跟踪定位站的时刻与到达主跟踪定位站的时间差为:
对式(24)和式(25)进行计算,可以获得对应的双曲面方程:
已知当前模型的观测值为∆ti,而被测目标到达主跟踪定位站和辅助跟踪定位站的距离之差为d0-di=c∆ti,其中i=1,2。将此处所算得的距离差c∆ti作为ΤDOA 的观测值。因此,当j=2 时,观测值为:
如图5 所示,本传感器管理算法主要分为两个部分,分别是状态转移矩阵更新和雷达辐射控制。
首先进行状态转移矩阵更新。在航迹起始时刻,通过检测前跟踪算法获得目标运动状态,取自k-L+1 起的L个目标运动状态值进行特征值提取。为了提高轨迹模型识别的准确性,分别把机动目标的帧间轨迹均值M、轨迹转角θk、瞬时速度vk和平均速度vˉ四个空间特征作为特征值选取依据。
在进行特征值提取后,使用第3 小节所述的多特征融合聚类算法对当前目标的L个运动状态进行融合聚类,从而获得目标当前的轨迹模型,并根据轨迹模型推断出目标当前状态转移矩阵通式Ft。
在使用多传感器协同管理算法进行目标跟踪时,同样使用第3 小节提出的波动参数作为状态转移矩阵更新的依据。假设在多传感器协同管理模式下阈值为,则说明目标跟踪算法误差激增,目标t轨迹突变,此时再次获取当前目标t的L个运动状态。对目标t的L个运动状态进行特征值提取、多特征融合聚类,并通过估计目标运动状态参数获得目标状态转移矩阵,最后将更新的目标状态转移矩阵赋予目标跟踪算法进行下一轮跟踪。
在雷达辐射控制部分,为了对当前多传感协同管理算法的准确性进行判断,从而进行传感器的最优分配,本文以本征堆积误差作为传感器决策依据。本征堆积误差是指目标t从q时刻到k时刻相邻间隔内协方差矩阵迹之差的堆积值,即
其中,Tr是指该矩阵的迹。
5 仿真结果
不失一般性,跟踪过程在建立的二维X-Y坐标系中实现。坐标系中,目标1 的初始位置为(0 m,0 m),初始速度为(100 m/s,100 m/s),目标2的初始位置为(500 m,2000 m),初始速度为(100 m/s,-100 m/s)。雷达在方位上的量测误差为±10 m;雷达和无源传感器量测最小间隔为1 s,采样点数为80。目标1初始运动模型为匀速直线模型,在第41个采样时刻开始突变为协同拐弯模型,并以该模型继续运动直到量测结束。目标2初始运动模型为协同拐弯模型,在第31 个采样时刻开始突变为匀速直线模型,并以该模型继续运动直到量测结束。
5.1 轨迹聚类测试
本文模拟机动目标不同运动模型,将150 个轨迹样本作为多特征融合轨迹聚类算法的处理对象,其中有60 根匀速直线运动模型的曲线,50 根协同拐弯运动模型的曲线,以及40根匀速直线与协同拐弯相混合的曲线。
分别使用单特征轨迹聚类算法和多特征轨迹聚类算法对轨迹进行聚类,得到下表1 所示的结果。
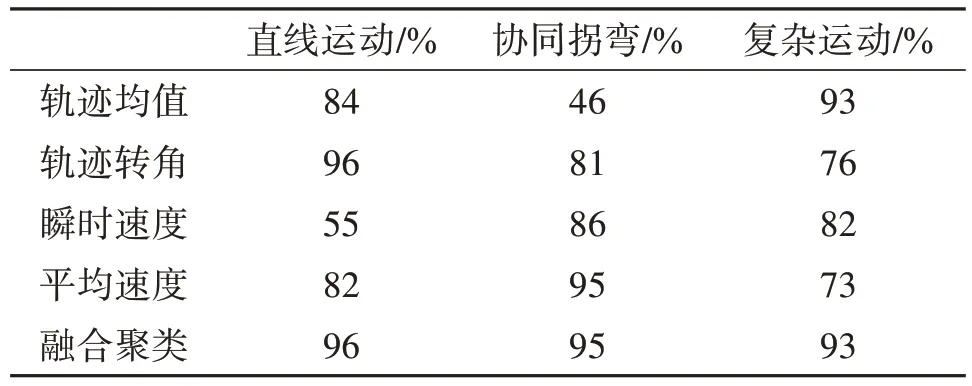
表1 二维坐标系轨迹聚类结果图Tab.1 Two-dimensional coordinate system locus-clustering result graph
如表1 所示,使用单特征的轨迹聚类算法对于不同的运动模型具有不同的识别精度,如对轨迹均值的聚类在面对复杂运动时识别度较高,对协同拐弯的识别度较低,这也就导致使用单特征轨迹聚类算法不能将上述150个不同运动模型的轨迹样本进行准确分类。而使用多特征融合的轨迹聚类算法能够对于不同的运动模型使用对其识别精度较高的轨迹特征进行聚类,从而有效提升了轨迹聚类的精度,实现轨迹样本正确分类,有利于实现状态转移矩阵的更新。
5.2 高机动多目标的无源跟踪
分别使用传统EKF 和IMM-EKF,以及本文提出的HMMΤ-EKF 作为无源目标跟踪算法进行高机动目标跟踪。其中每一个时刻每一个目标的周围±1000 m 内会产生n个杂波,n服从上限为10,下限为0 的均匀分布。同时,每一个目标的检出概率PG=0.9。
对80个采样间隔内目标轨迹进行跟踪,EKF和IMM-EKF 的目标跟踪点迹如图7 所示,HMMΤEKF的目标跟踪点迹如图8所示。

图7 EKF和IMM-EKF的无源多目标跟踪点迹图Fig.7 Passive multi-target trace graphs of EKF and IMMEKF results
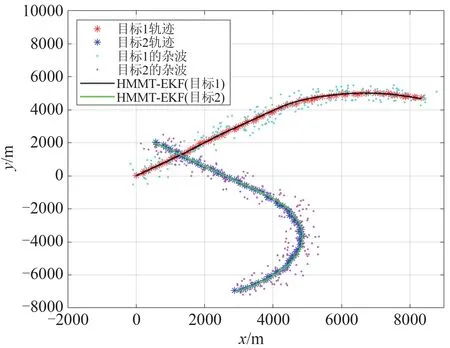
图8 HMMΤ-EKF的无源多目标跟踪点迹图Fig.8 Passive multi-target trace graph of HMMΤ-EKF results
在前30 个采样时刻,1 号目标和2 号目标均做匀速直线运动,三种算法的初始状态转移为匀速直线模型,状态转移矩阵为:
在第31 个采样时刻,2 号目标运动模型由匀速直线运动转化成ω=0.75π 的匀速转弯运动。此时,EKF 仍保持原状态转移矩阵不变,IMM-EKF 算法由于先验模型未知,仍以原始的转移概率矩阵进行目标的跟踪。HMMΤ-EKF 在第32 个采样时刻由于波动误差超过门限值触发状态转移矩阵更新决策,第32~34个采样时刻由于聚类算法正在进行中,状态转移矩阵尚未成功更新;第35个采样时刻聚类算法完成聚类,将状态转移矩阵更新为,即
在第41 个采样时刻,1 号目标运动模型由匀速直线运动转化成匀速转弯运动。此时EKF 仍保持不变,IMM-EKF 算法仍以原始的转移概率矩阵进行目标的跟踪。HMMΤ-EKF 在第42 个采样时刻由于波动误差超过门限值触发状态转移矩阵更新决策,并在接下来的2个采样间隔进行轨迹聚类;第45个采样时刻聚类算法完成,将状态转移矩阵更新为,即
为了对三种算法的跟踪误差进行对比,本文以均方根误差(Root mean square error,RMSE)作为评判标准,绘制了如图9 所示的三种无源多目标跟踪算法的目标跟踪误差图。

图9 三种无源多目标跟踪算法的目标跟踪误差图Fig.9 Multi-target tracking-error graphs of results from three passive target-tracking algorithms
由图9可知,EKF和HMMΤ-EKF算法目标运动状态模型尚未改变时RMSE 类似,略高于IMMEKF。但当目标运动模型发生变化后,由于EKF 不会更新目标的状态转移方程,因此在目标发生机动以后产生较大误差,最终RMSE 为三种算法中最高。IMM-EKF 是不同目标运动模型加权的结果,因此RMSE 低于EKF。而HMMΤ-EKF 由于自适应更新状态转移矩阵,因此目标运动模型转变的几个采样时刻后进行了状态转移矩阵的正确更新,因此在三种目标跟踪算法中RMSE最低。
5.3 多传感器协同管理
在5.2 节三种多目标无源跟踪算法的基础上引入雷达间歇辐射进行误差修正,即将无源目标跟踪算法应用到多传感器协同管理算法中并进行仿真,得到如图10 所示的基于EKF 和IMM-EKF 的传感器管理算法多目标跟踪点迹图,如图11所示的基于多传感器协同管理算法的多目标跟踪点迹图,以及如图12所示的三种算法跟踪误差图,跟踪误差同样以RMSE为评判标准。
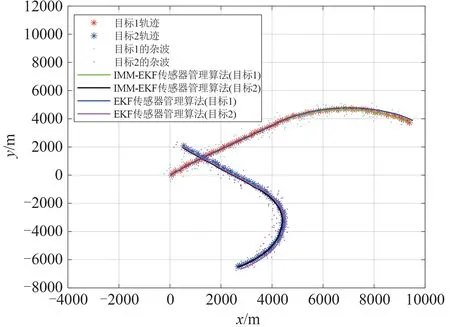
图10 基于EKF和IMM-EKF传感器管理算法的多目标跟踪点迹图Fig.10 Multi-target tracking point trace based on EKF and IMM-EKF sensor management algorithms

图11 基于轨迹聚类的多传感器协同管理算法的多目标跟踪点迹图Fig.11 Multi-target tracking point trace map of results from multi-sensor cooperative management algorithm based on trajectory clustering
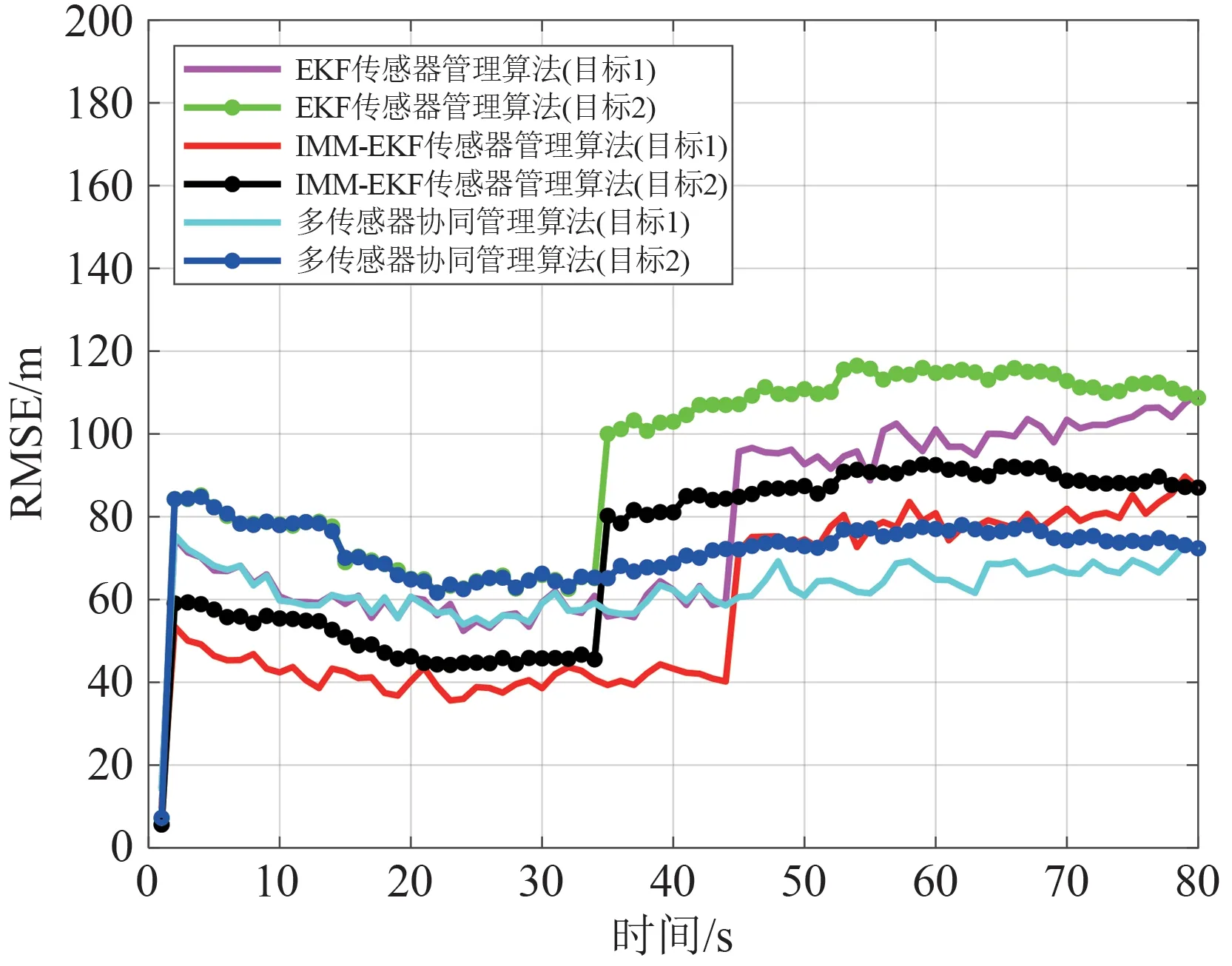
图12 三种传感器管理算法的目标跟踪误差图Fig.12 Τarget tracking error graphs of three sensor management algorithms
在目标运动模型发生改变前,由于雷达辐射参与修正,基于EKF 传感器管理算法和基于轨迹聚类的多传感器协同管理算法的误差值均在一定范围内波动,且雷达辐射次数相似,略高于基于IMMEKF传感器管理算法。
在目标运动模型发生改变后,由于目标状态转移矩阵无法更新,使用基于EKF 传感器管理算法对目标1 和2 跟踪结果RMSE 较大,雷达辐射次数较多,在80 个仿真间隔内共辐射36 次。基于IMMEKF 的传感器管理算法的RMSE 略低于基于EKF传感器管理算法,在80个仿真间隔内共辐射28次。
基于轨迹聚类的多传感器协同管理算法由于状态转移矩阵的实时更新,其跟踪算法精度较高,雷达辐射次数较少,在80 个采样间隔内共辐射20 次,远低于基于EKF 的传感器管理算法和基于IMMEKF 的传感器管理算法。因此,本文所设计的基于轨迹聚类的多传感器管理算法能在提升跟踪精度的同时减少雷达辐射次数,有利于实现低截获概率跟踪。
对于基于轨迹聚类的多传感器协同管理算法,本文选取了不同本征堆积误差门限对目标进行跟踪仿真,并对其雷达辐射次数和平均RMSE 做了统计,如下表2所示。
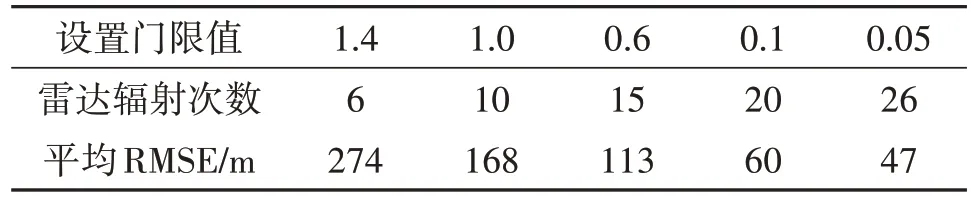
表2 本征堆积误差门限统计表Tab.2 Intrinsic accumulation error threshold statistics
由表2 可知,本文所设计的传感器管理算法在机动目标跟踪时,若门限设置过小平均估计误差虽较小,但雷达辐射次数较多,不利于雷达低截获概率跟踪;而当门限设置过大时,雷达辐射次数虽减少,但其平均估计误差较大。因此统计得出在应对高机动目标时门限值设置在0.1左右时为最佳。
此外,在雷达门限值为0.1 时,本文还选取了不同的波动参数阈值进行跟踪仿真,并对他们的辐射次数和平均估计误差进行统计,如下表3所示。
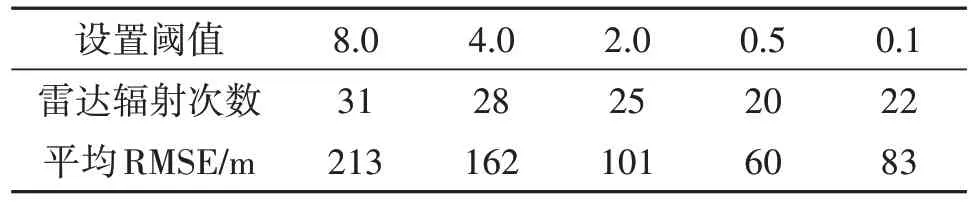
表3 波动参数阈值统计表Tab.3 Statistical table of fluctuation parameter thresholds
由表3 可知,波动参数阈值的设置对雷达辐射次数和平均估计误差也有较大的影响。当阈值过大时,模型不能及时更新状态转移矩阵,雷达辐射次数较多,且平均估计误差较大;若阈值过小,需要轨迹聚类次数过多,而每次聚类需要多个仿真间隔,因此会造成轨迹聚类堵塞现象,从而造成雷达辐射次数增多和平均估计误差增大。所以,阈值设置为0.5左右时为最佳。
6 结论
本文针对高机动目标运动模型未知引起的低跟踪精度问题,首先提出了HMMΤ-EKF 算法。该算法将跟踪波动参数,即相邻两个间隔内滤波算法预测值与观测值误差之差,作为目标跟踪性能指标,进行目标轨迹聚类与运动模型参数估计判决,从而完成目标状态转移矩阵的更新,解决了传统目标跟踪算法不适用高机动多目标跟踪的问题。在此基础上,考虑到无源传感器不对外辐射能量,具有较好的低截获概率性能,本文提出了一种基于轨迹聚类的多传感器协同目标跟踪算法。该算法通过对目标跟踪本征堆积误差即相邻间隔内预测协方差矩阵迹之差的堆积值的判断进行传感器的最优分配,并根据目标跟踪波动参数进行状态转移矩阵更新决策,从而有效减少雷达辐射次数。仿真分析了基于多传感器协同管理的多目标跟踪误差和雷达辐射次数,并对本征堆积误差门限和波动参数阈值的设置进行讨论。仿真结果表明,本文所设计的HMMΤ-EKF 算法能显著提升无源传感器对高机动目标跟踪精度,且基于轨迹聚类的多传感器协同目标跟踪算法在确保高机动多目标跟踪精确度的同时能进一步减少雷达辐射次数,提升作战平台的低截获概率性能。
