基于多普勒偏移补偿的非线性FDA-MIMO雷达运动目标检测算法
2024-03-07丁俊淞张顺生王文钦
丁俊淞 张顺生* 王文钦
(1.电子科技大学电子科学技术研究院,四川成都 611731;2.电子科技大学信息与通信工程学院,四川成都 611731)
1 引言
为了克服传统相控阵只能产生角度维依赖的发射波束[1]的问题,美国空间研究实验室Antonik等人提出了频控阵[2](Frequency Diverse Array,FDA)的雷达体制,其通过给不同阵元的载频施加频偏以产生在角度和距离均具有依赖性的波束,频控阵在雷达领域的发展也在近年来引起了广泛的关注[3-5]。FDA 雷达通过在不同阵元间设置一定的载波频偏,这使得雷达发射方向图由相控阵的角度函数变为距离-角度-时间的多元函数,其为提升FDA 雷达探测目标的性能提供了其他维度的信息[6-7]。然而FDA 雷达的发射导向矢量中距离和角度相互影响,这会使得距离和角度的参数估计难以进行。为了获得距离维的自由度[8],可以利用多输入多输出(Multiple Input Multiple Output,MIMO)技术来解耦发射波形。FDA-MIMO 雷达近年来被学者应用于距离模糊杂波抑制[9-10]、距离角度联合参数估计[11-12]、目标检测[13-14]等研究方向。传统的线性频偏FDA 雷达在波束方向图上是距离-角度耦合并且时变的,虽然可以通过设置非线性频偏获得距离-角度解耦的波束方向图,但其依然是时变的。而利用非线性FDA-MIMO雷达可以即获得距离-角度解耦同时不变的波束方向图[15]。这将使得非线性FDAMIMO 雷达在抗主瓣干扰领域相比线性FDA 雷达有更大的优势。
针对FDA-MIMO 雷达运动目标检测,Huang 等人[16]在考虑高斯杂波的情况下研究了未知协方差矩阵的FDA-MIMO 雷达分布式目标检测,提出了一种基于无训练数据的两步法(Generalized Likelihood Ratio Τest,GLRΤ)准则的检测器,提高了雷达的目标检测性能。Gui等人[17]提出了一种基于(Unstructured Generalized Likelihood Ratio Τest,UGLRΤ)的检测方法,将3 维搜索转化为1 维多普勒和联合距离-角度搜索,与传统的(Structured Generalized Likelihood Ratio Τest,SGLRΤ)相比UGLRΤ 在不降低检测和估计性能的前提下显著降低了计算复杂度。上述文献的推导过程中并没有涉及多普勒偏移效应。而在实际应用中,回波的多普勒偏移效应会随着目标的高速运动,阵元数量的增加和阵元间频偏的增大而越来越明显。针对多普勒偏移效应,Zhang 等人[18]提出了基于插值滤波的重采样算法,可以使得目标的多普勒偏移和跨距离单元走动在无需估计目标速度的情况下被消除。
基于插值滤波的重采样算法虽然可以在小频偏的情况下获得良好的目标检测效果,但是当雷达采用非线性频偏时由于阵元间的载频差异不再可以忽略,导致上述算法性能下降。本文提出一种基于速度搜索的多普勒偏移补偿算法,可以在非线性频偏体制下准确的补偿回波多普勒偏移,实现信号能量的相干积累,使雷达的目标检测性能得到提高。
2 信号模型与问题分析
2.1 非线性FDA-MIMO雷达运动目标模型
图1 是非线性FDA-MIMO 雷达发射接收阵列模型,发射和接收共用一个阵元,d表示阵列的阵元间距。sm,m=0,1,…,M-1和rn,n=0,1,…,N-1分别表示第m个阵元的发射信号和第n个阵元接收到来自远场目标的回波信号。

图1 FDA-MIMO雷达发射接收阵列模型Fig.1 Τransmit-receive array model of FDA-MIMO radar
假设第1 个发射阵元的发射载频为fc,0,则第m个阵元的发射信号对应的载波频率如式(1)所示:
其中M表示发射阵元数,Δf表示基本频偏。
假设FDA-MIMO 雷达发射的基带信号为线性调频信号(Linear Frequency Modulated,LFM),目标以径向速度v向雷达飞来,通过脉冲串的形式在慢时间域进行多普勒测量,可以得到第m个发射阵元的发射基带信号如式(2)所示:
其中rect(·)表示门函数,t表示快时间,μ表示调频斜率,Tp表示脉冲宽度。
假设初始时刻目标与雷达之间的径向距离为RT,忽略高阶分量,目标分别与第n个接收阵元间和第m个发射阵元间的径向距离之和如式(3)所示:
其中tk表示慢时间,则接收阵列的N维回波信号矢量如式(4)所示:
其中A(θ)表示发射-接收联合导向矢量,表示为式(5),ΩD(t,v)表示多普勒频移矩阵,表示为式(6),S(t)表示基带发射信号矩阵,表示为式(7),Fc(t)表示发射信号的载波向量,表示为式(8)。τ(tk)表示目标与雷达间的双程延时,表示为式(9)。
2.2 距离徙动分析
对式(4)做脉冲压缩后可得到接收阵列对回波信号进行脉冲压缩后的N维回波信号矢量,如式(10)所示:
其中E(θ)表示为脉冲压缩后的信号幅度,Sc(t)表示脉冲压缩后的基带回波信号,如式(11)所示:
从式(10)中可以看出,慢时间会影响回波信号的包络位置,当包络的变化程度超过一个距离分辨率后就会导致距离徙动的产生,使不同脉冲的回波能量无法聚焦在同一距离门。
2.3 插值滤波重采样算法问题分析
假设ran,m(t,k)表示第n个接收阵元的第m个通道在第k个快拍得到的信号,在快时间域做快速傅里叶变换(Fast Fourier Τransform,FFΤ)得到快时间频域-慢时间时域信号,如式(12)所示:
由于慢时间域的欠采样,导致目标的真实速度v=Qvpr+v0,其中Q表示最大不模糊速度对真实速度的折叠因子,同时该折叠因子可以通过构造补偿函数消除[18],表示第m个通道的盲速,v0是真实速度对盲速取余后的不模糊速度。式(12)在慢时间域的采样率为,采用新的采样率对式(12)进行重采样可得到式(13):
由于各发射阵元的基带信号为窄带信号,所以在阵元数不是很大的情况下有MB≪fc,0,基于窄带假设。当阵列采用线性频偏时fc,m≈fc,0,所以,故可以由式(13)得到式(14):
如图2 和图3 所示,与线性频偏相比,非线性频偏会给接收阵元的各个通道带来更大的载波频差,导致更大的多普勒偏移。这将导致上述条件fc,m≈fc,0不再成立,故式(14)将不再成立。所以针对插值滤波重采样算法[18]的上述不足,本文提出一种基于速度搜索的多普勒补偿方法。

图2 非线性频偏距离多普勒图Fig.2 Range-Doppler map with nonlinear frequency offset
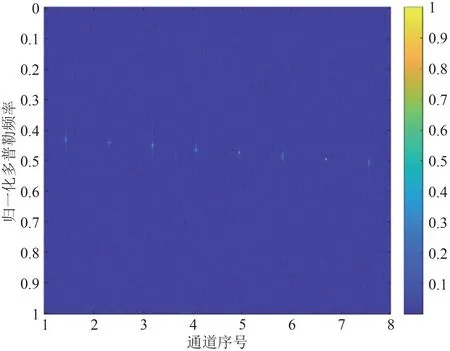
图3 线性频偏距离多普勒图Fig.3 Range-Doppler map with linear frequency offset
3 基于速度搜索的多普勒补偿方法
本文提出了一种新的算法,可以利用Keystone变换和多普勒偏移补偿函数的方法,来消除目标速度导致的距离走动和不同载频间频偏导致的多普勒偏移。首先利用Keystone变换去除雷达回波的距离徙动,然后通过构造补偿函数去除频偏导致的多普勒偏移,最后对目标进行相参积累,实现目标检测。
3.1 Keystone变换
首先利用Keystone 变换校正由目标速度造成的距离徙动,在快时间频域-慢时间域做如下变换:
其中An,m(θ)表示第m个发射阵元和第n个接收阵元的联合导向矢量。如式(16)所示,回波信号经Keystone变换后v和f之间的耦合已经消除,距离徙动得到校正。
3.2 多普勒补偿算法
由式(10)提取出第n个接收阵元中第m个通道的辐射信号脉冲压缩后的结果如式(17)所示:
根据式(17)的最后一项可以看出,目标速度和阵元间频偏会导致不同接收阵元的由于回波信号的多普勒频率不一致,使得回波信号无法形成相干叠加,从而降低了检测性能。为了解决上述问题,定义式(18)的速度补偿函数。
其中m表示发射阵元序号,vs表示待搜索的目标速度。将式(18)乘以式(17)得到补偿后的回波信号如式(19)所示:
当搜索的目标速度vs等于目标的真实速度v时,式(19)中由于频偏造成的多普勒偏移将会被补偿。通过对(19)在慢时间域做FFΤ可得式(20):
其中FFΤ[·]表示对信号做FFΤ,AFΤ(θ,t,tk)表示信号FFΤ 后的幅度,δ(·)表示冲激函数,fk表示慢时间FFΤ后的变量,⊛表示卷积。
如果艾滋病患者或艾滋病病毒携带者有故意传播艾滋病的行为,比如,艾滋病患者不告知或故意隐瞒自己的病情,通过性行为或者通过其他方式将艾滋病传染给了特定的某一个人,就危害到了这个特定人的生命健康。我们都知道艾滋病目前尚不可治愈,被传染者的生存权利就被无形地剥夺。
由于第1个发射阵元的辐射信号不存在频偏引起的多普勒偏移,所以可通过设置合理的范围对vs进行一维搜索,搜索函数如式(21)所示:
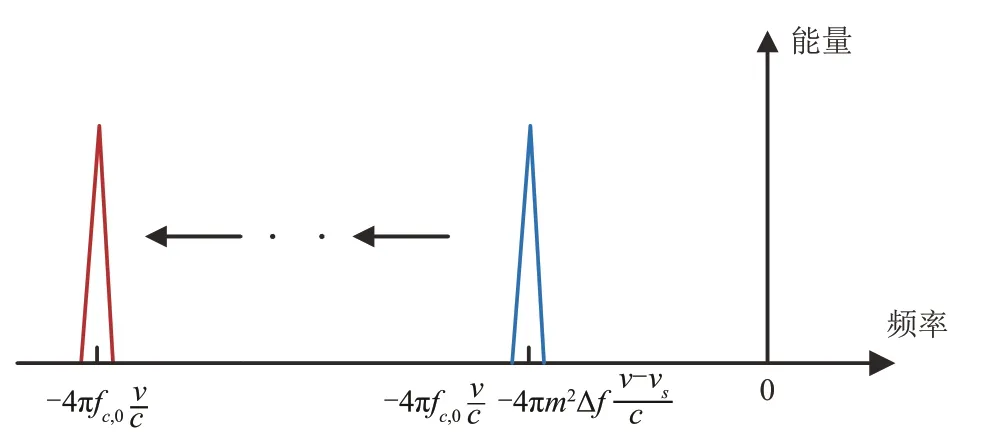
图4 速度搜索示意图Fig.4 Sketch map of speed search
图5 是非线性FDA-MIMO 雷达动目标检测流程图。本流程首先对雷达回波信号做多通道混频匹配滤波,然后利用Keystone 变换消除目标回波的距离徙动,接着根据阵元间频偏构造多普勒补偿函数,再将该补偿函数乘上变换后的结果并沿慢时间域做FFΤ,随后通过一维搜索寻找峰值得到目标速度并补偿,完成相干积累采用恒虚警(Constant False Alarm Rate,CFAR)检测器完成目标检测。
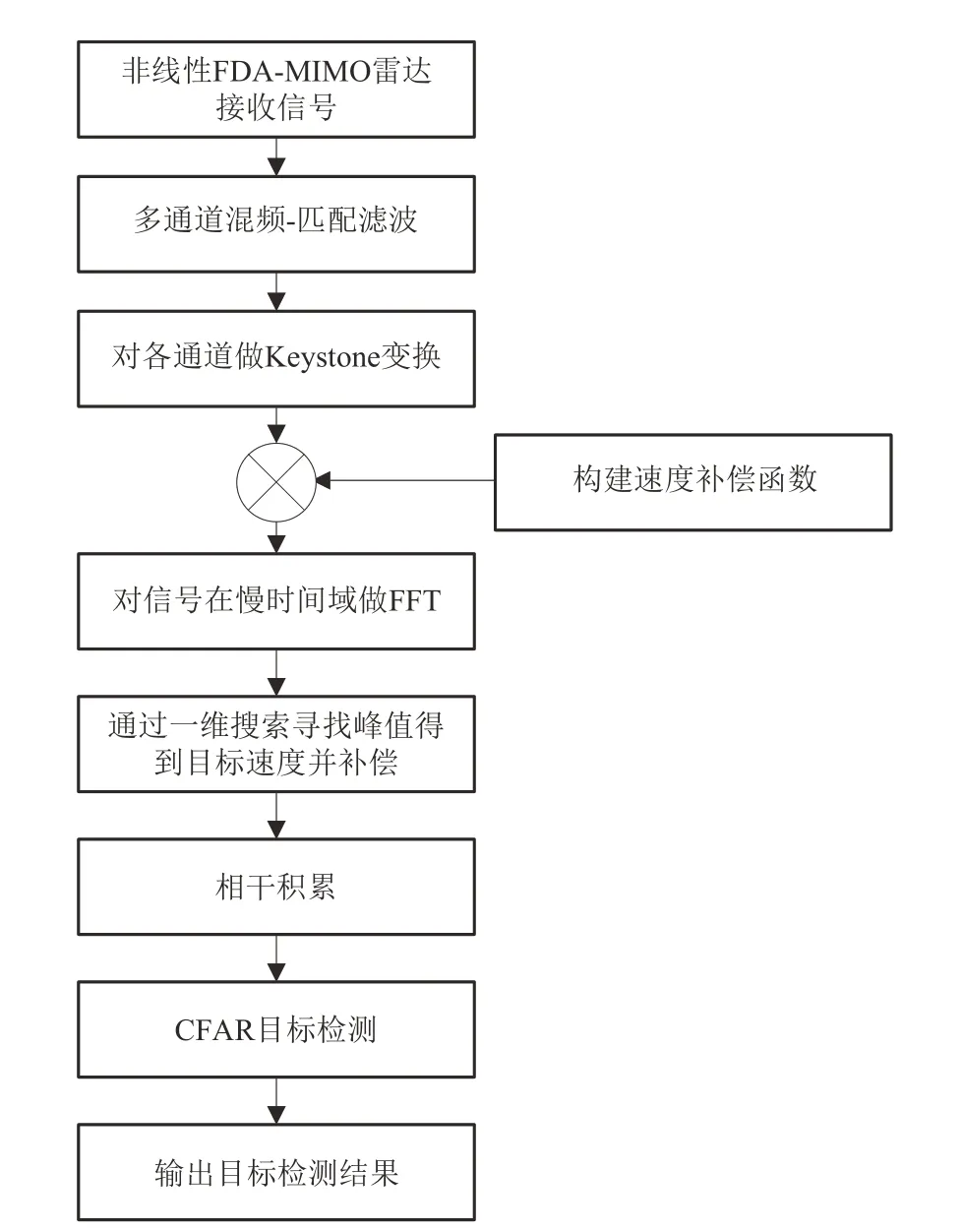
图5 非线性FDA-MIMO雷达动目标检测流程图Fig.5 Flowchart of moving target detection with nonlinear FDA-MIMO radar
4 仿真分析
为验证本文所提的目标检测算法性能,采用数值仿真对多普勒补偿算法进行仿真分析,仿真设置8 个发射阵元和8 个接收阵元,发射和接收阵元间距设置为半波长,雷达各阵元的载波采用平方递增,既第m个发射阵元的载波fc,m=fc,1+m2Δf。假设目标初始距离为50 km,目标初始速度为347.48 m/s,目标与雷达夹角为60°,雷达回波信噪比为-10 dB,具体雷达参数如表1所示。

表1 雷达参数Tab.1 Radar parameters
图6为采用本文所提算法和插值滤波重采样算法得到的各通道距离-多普勒图,从图6(a)中可以看出本文所提算法将所有通道的多普勒偏移均进行了合适的补偿。图6(b)可以看出当频偏相对于载频较小时插值滤波重采样算法可以补偿多普勒偏移,但随着频偏的增加该算法将无法正确的补偿多普勒偏移。
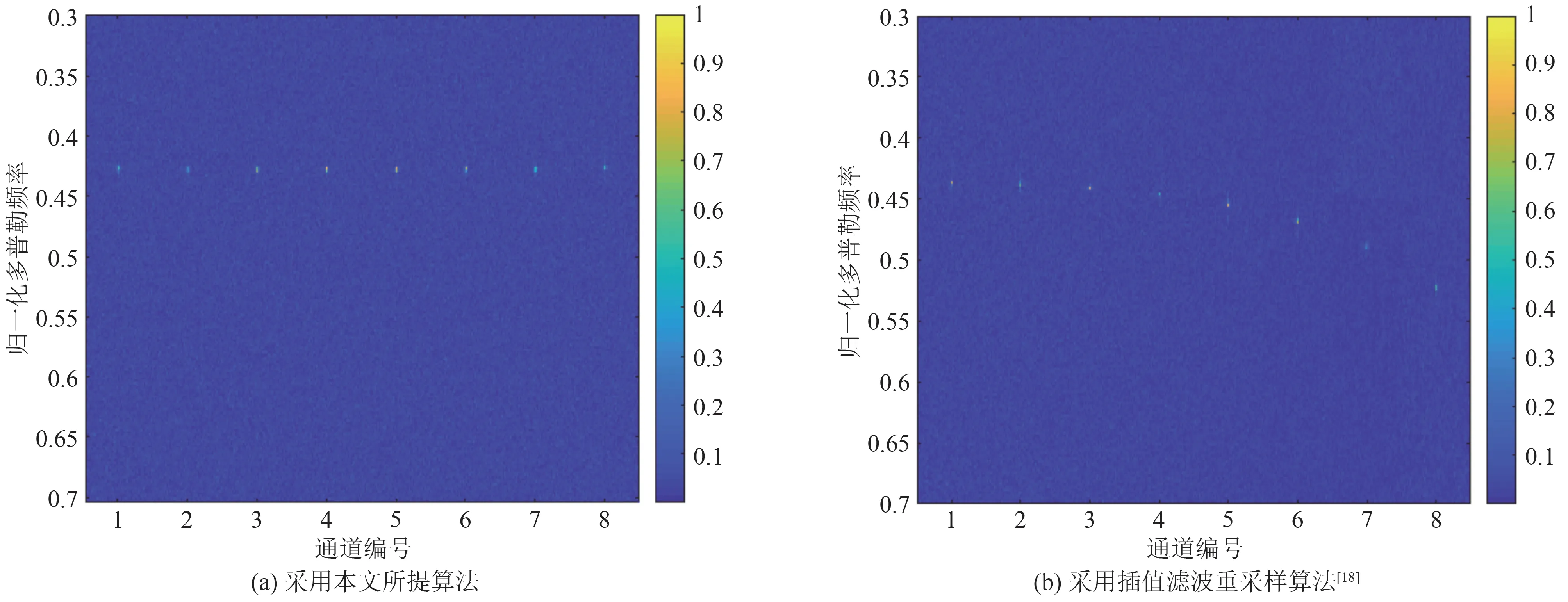
图6 第一个接收阵元采用不同处理算法得到的各通道的距离-多普勒图Fig.6 Range-Doppler maps of each channel from the first receiving element using different algorithms
通过FDA-MIMO 雷达的速度分辨率可以设置合适的速度搜索网格,根据表1 的参数可以得到此时雷达的速度分辨率为0.73 m/s。图7(a)为设定搜索网格为0.75 的情况下,对各通道信号进行相干积累得到的结果。可以看出,当搜索网格大小与速度分辨率相等时,相干积累后能量聚焦在了同一个多普勒单元。图7(b)为设定搜索网格为1.5 的情况下,对各通道信号进行相干积累得到的结果。可以看出,由于速度网格的增大,搜索的精度受到影响,峰值能量出现了一定程度的降低。当实际进行速度搜索时,无需使网格设置接近于速度分辨率也能获得可接受的效果,同时由于扩大了搜索网格,算法耗时也将下降。
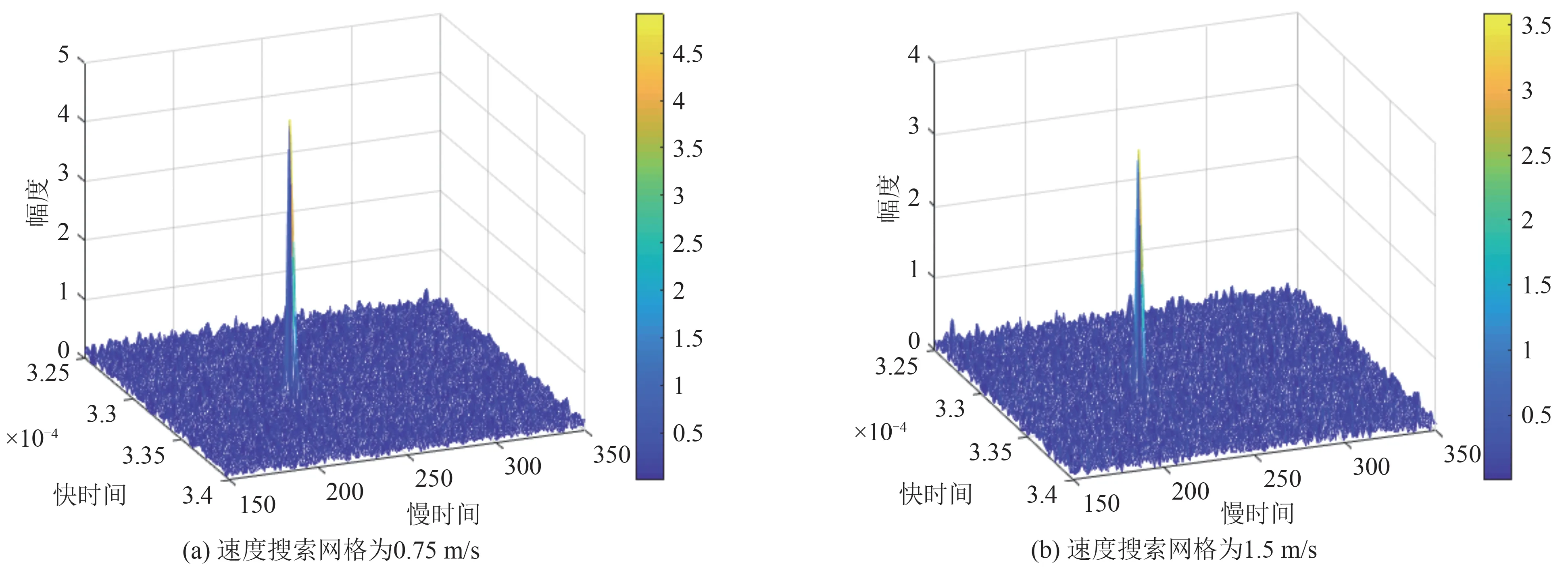
图7 不同速度搜索网格下的相干积累结果Fig.7 Coherent accumulation results under different speed search grids
图8为相参处理增益随频偏变化曲线图。从图中可以看出当随着频偏从1 MHz 变化到9 MHz 时本文所提算法的相参积累增益基本不变,并且当频偏较小时,文献[18]所提算法能在一定程度上补偿多普勒偏移,但随着频偏增大相参积累增益逐渐下降。
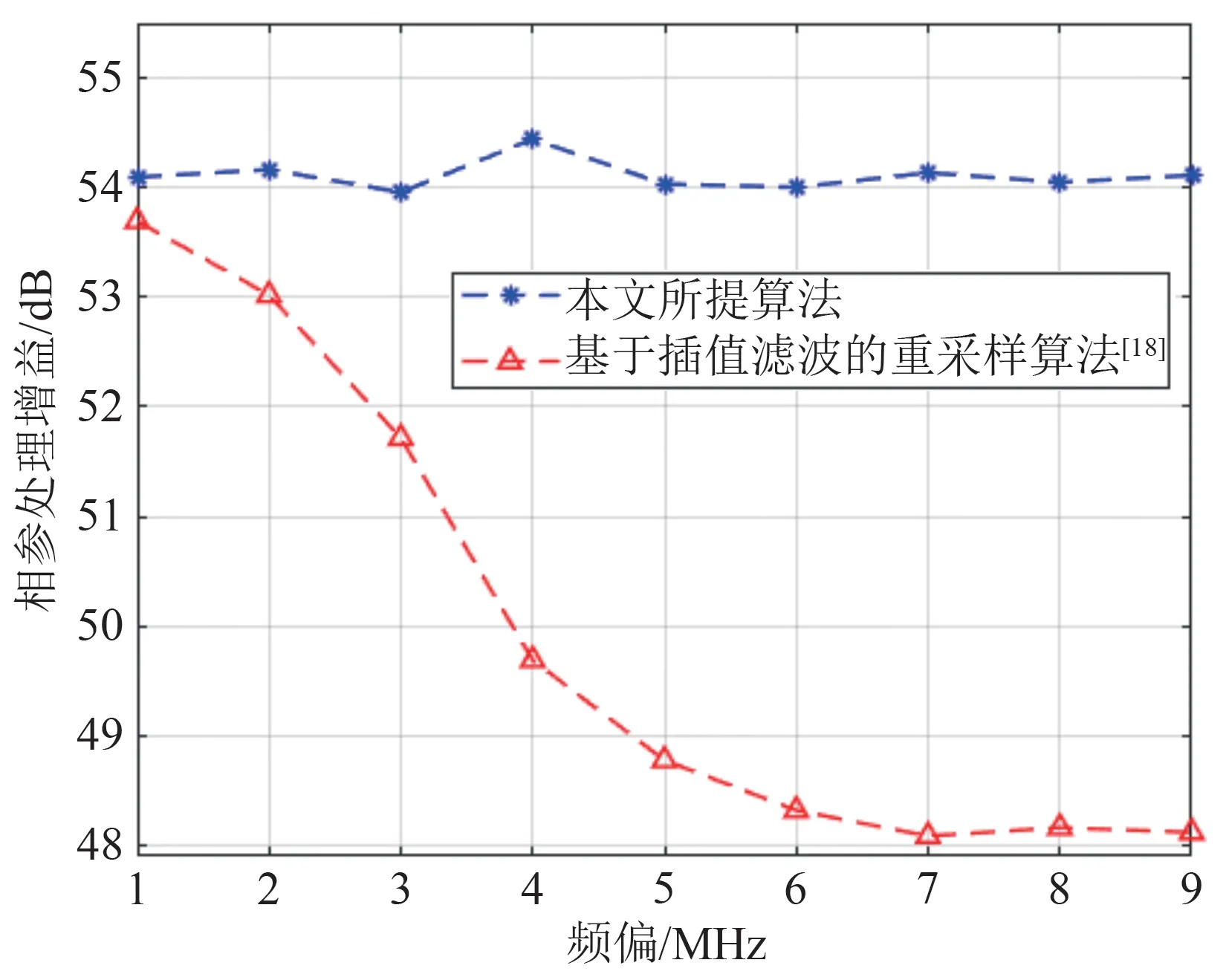
图8 相参处理增益随频偏的变化Fig.8 Variation in coherent processing gain with frequency offset
图9 是设定虚警率为10-4时,传统算法,本文所提算法和基于插值滤波的重采样算法[18]经过10000次蒙特卡洛仿真得到的检测概率曲线。基于插值滤波的重采样算法会随着发射阵元载频的增大造成检测性能的下降而使通道间无法相干积累。而传统算法在非线性FDA-MIMO 雷达体制下无法补偿各通道间的多普勒偏移,其检测性能有稍差与文献[18]所提算法。本文所提算法能在阵元载频远大于基本载频时实现多普勒偏移的补偿,与基于插值滤波的重采样算法相比能在更低的信噪比下获得良好的目标检测性能。
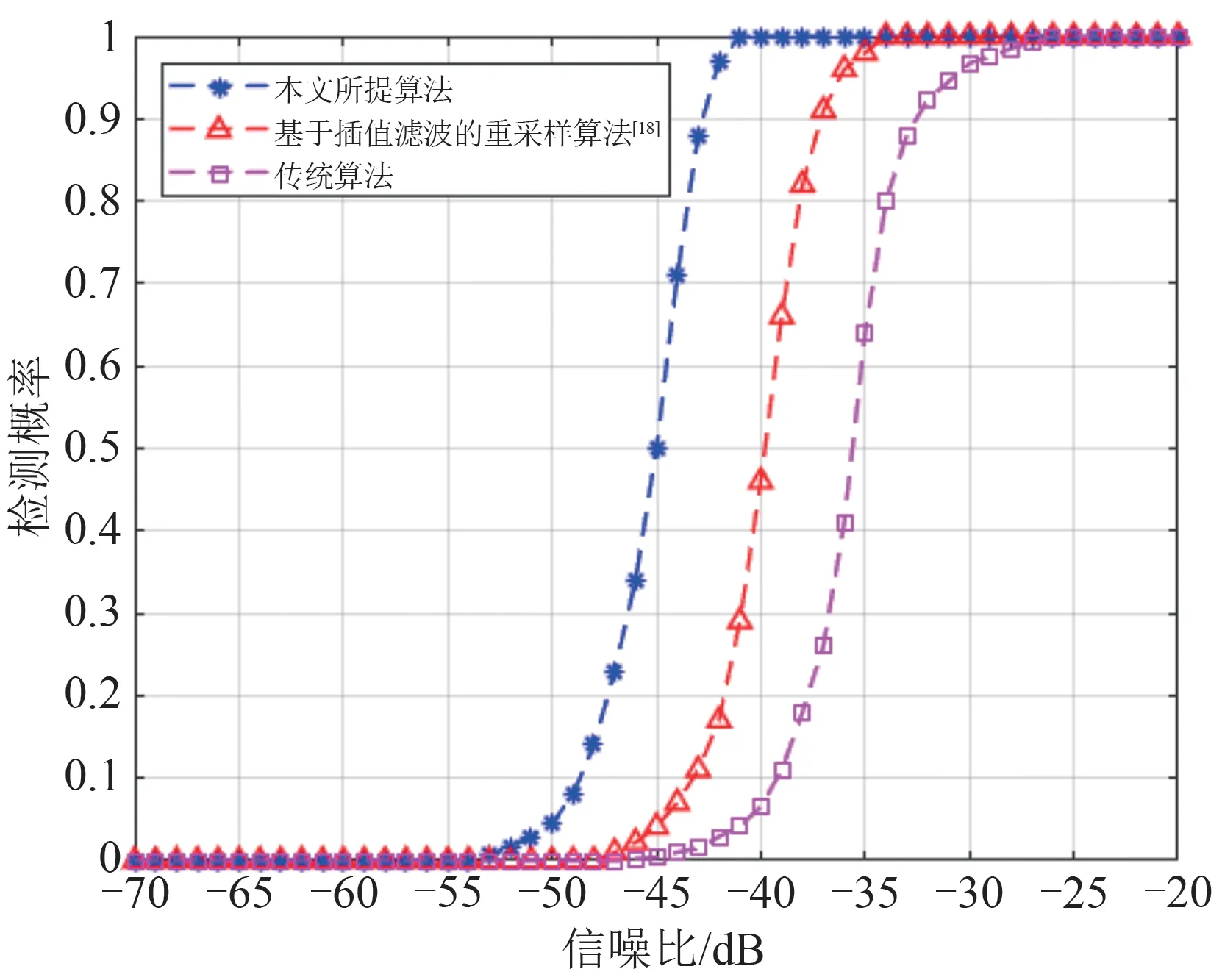
图9 三种算法的检测概率对比Fig.9 Comparison of detection probability results of three algorithms
5 结论
为了解决非线性FDA-MIMO 雷达动目标检测中由于频偏不再线性变化导致文献[18]所提算法失效的问题,本文提出了一种基于速度搜索的多普勒偏移补偿算法。该方法能够准确地补偿阵元间的多普勒偏移,解决了非线性FDA-MIMO 雷达体制下的动目标检测问题。需要说明的是,本文所提算法考虑的是匀速运动的目标模型,并未考虑加速度对多普勒频率带来的影响,下一步的工作是如何补偿变速运动目标的多普勒偏移。
