Consequences of Rényi entropy on the thermal geometries and Hawking evaporation of topological dyonic dilaton black hole

Muhammad Yasir ,Xia Tiecheng ,Muhammad Usman and Shahid Chaudhary,*

1 Department of Mathematics,Shanghai University and Newtouch Center for Mathematics of Shanghai University,Shanghai,200444,China

2 Department of Natural Sciences and Humanities,University of Engineering and Technology Lahore,New Campus,Pakistan

Abstract The thermodynamics of black holes (BHs) has had a profound impact on theoretical physics,providing insight into the nature of gravity,the quantum structure of spacetime and the fundamental laws governing the Universe.In this study,we investigate thermal geometries and Hawking evaporation of the recently proposed topological dyonic dilaton BH in anti-de Sitter(AdS)space.We consider Rényi entropy and obtain the relations for pressure,heat capacity and Gibbs free energy and observe that the Rényi parameter and dilaton field play a vital role in the phase transition and stability of the BH.Moreover,we use Weinhold,Ruppeiner and Hendi Panahiyah Eslam Momennia models to evaluate the scalar curvature of the BH and find out that the divergence points of the scalar curvature coincides with the zero of specific heat.Finally,using Stefan–Boltzmann law,we determine that the BH without a dilaton field evaporates far more quickly compared to the dilaton BH in AdS space.

Keywords: topological dyonic dilaton black hole,phase transition,thermal geometry,Hawking evaporation

1.Introduction

The study of the geometric structure of black holes (BHs)within the framework of general relativity (GR) and alternative gravity theories stands out as an intriguing and demanding subject [1].Thermodynamics of BHs is a fascinating topic that combines principles from GR and thermodynamics.Hawking and Bekenstein started work on the thermodynamics of BHs and showed that they possess certain thermodynamic properties.The well-established four laws of BH mechanics are employed to analyze the thermal properties and behavior of BHs [2,3].Bekenstein proposed that BHs have entropy which is directly related to horizon area.This implies that BHs possess a large number of microscopic states,similar to thermodynamic systems,even though they are objects of extreme gravitational collapse.Later,Hawking showed that BHs are not completely black but emit a form of radiation now known as Hawking radiation.This radiation arises due to quantum effects near the event horizon,and they carry away energy from the BH,causing them to gradually lose mass and eventually evaporate.

Recently,the thermal analysis of BH in anti-de Sitter(AdS) space has been comprehensively investigated in the extended phase space where the cosmological constant Λ is taken as the thermodynamic variable[4–8].Kubiznk and Mann[7,9] studied the P-V criticality of BH in extended phase space and provided important results on the liquid gas systems and phase transitions.Davies [10] studied phase transition through thermal analysis of the BH and obtained high-ordered phase transitions.Husain and Mann [11,12] showed that heat capacity of the BH becomes positive when phase transition reaches the Plank scale.Another result in BH physics is the van der Waals liquid gas phase transitions of charged AdS BHs[13].In AdS space,Hawking–Page phase transition occurs enclosed by a stable large BH,and thermal gas,[14] which is illustrated as the confinement and deconfinement phase transition of a gauge field[15].Chamblin et al[16]discussed phase structures of an electrically charged BH and showed its analogy to a van der Waals phase transition.

Hawking radiation arises from the application of quantum field theory near the event horizon of a BH.According to this theory,pairs of virtual particles constantly form and annihilate near the event horizon.Occasionally,one particle from the pair falls into the BH,while the other escapes to infinity as radiation.The escaping particle is observed as Hawking radiation.The temperature of Hawking radiation is inversely proportional to the mass of the BH.As the BH emits radiation,it loses mass,causing its temperature to increase.This process continues until the BH eventually exhausts its mass and completely evaporates.Hou et al[17]evaluated the Hawking evaporation of BHs in massive gravity and studied the influence of massive gravity on the evaporation process.Wu et al [18] discussed the evaporation process of Gauss Bonnet BHs in n ≥4 dimensions and provide the influence of higher dimensions on the evaporation process.

In our study,we consider recently introduced topological dyonic dilaton BHs in AdS space [19]and investigated some interesting thermodynamic aspects.These BHs are a specific class of BH solutions that arise in theories of gravity with additional fields,such as dilaton fields and gauge fields.These BHs possess both electric and magnetic charges,and they have nontrivial topological structures.These BHs are very important due to their close ties to the AdS/CFT correspondence,cosmic censorship and arise naturally in the context of string theory and supergravity.We consider Rényi entropy,which allows for the incorporation of quantum corrections to the thermodynamic properties of BHs.It provides a more versatile framework to study deviations from classical thermodynamics,especially in situations where quantum effects become significant.For a BH,the Rényi entropy is often employed to describe the entanglement entropy associated with the degrees of freedom outside and inside the event horizon.Understanding the Rényi entropy with varying Rényi parameter can shed light on the distribution of entanglement entropy across different energy scales and help discern the nature of correlations among the degrees of freedom inside and outside the event horizon.The study of thermal geometries and Hawking evaporation of topological dyonic dilaton BHs in AdS space can provide better insight into the nature of BHs.

The layout of the study is as follows.In section 2,we provide an overview of the new class of topological dyonic dilaton BHs in AdS spaces.In section 2.1,we uncover the impact of Rényi entropy on the thermodynamics of the BH.In section 2.2,we introduce thermal geometries of topological dyonic dilaton BHs.In section 2.3,we discuss the Hawking evaporation process for the BH.Finally,in section 3,we conclude by summarizing our results.

2.Brief review of topological dyonic dilaton BHs

The action of Einstein–Maxwell-dilaton gravity with dilaton potential is expressed as follows [19]:

whereR represents the Ricci scalar curvature,F2=FμνFμνis the Maxwell Lagrangian and V(Φ)denotes the potential for Φ,which can be written as follows:

where Λ represents the cosmological constant.The variation in action with respect to metric yields Maxwell and dilaton fields as follows:

The non-rotating spherically symmetric topological BH in 4D is given by(for the detailed solution we refer the reader to[19]):

where m and b are the mass and dilaton field of BH,and p and q manifest the magnetic and electric charges,respectively.In this context,the symbol k represents a dyonic dilaton parameter,giving rise to electric and magnetic fields through the application of Maxwell’s equations.A BH that possesses both electric and magnetic charges is termed a dyonic BH.These BHs serve as excellent subjects for investigating the impact of external magnetic fields on superconductors,as well as studying Hall conductance and DC longitudinal conductivity,as discussed in [20].Moreover,it has been proposed that a dyonic BH in an AdS background could serve as the holographic dual of a van der Waals fluid with a chemical potential[21].In addition,on the conformal boundary of AdS spacetime,the dual of these BHs corresponds to stationary solutions of relativistic magnetohydrodynamics equations[22].This is a very interesting solution and for the limiting case r →∞,the solution leads to asymptotically AdS due to the dominance of the cosmological constant.

2.1.The impact of Rényi entropy on the thermodynamics of the BH

The cosmological constant can be treated as thermodynamic pressure and after the inclusion of thermodynamic pressure P into the laws of thermodynamics,it is shown to be of significant importance in BH physics.Setting f(r)=0 and usingP=,we can easily obtain the mass of the BH as a function of horizon radius and pressure as follows [23–25]:

Figure 1 shows the plots of Hawking temperature T versus horizon radius rhof the topological dyonic dilaton BH for fixed values of q=0.064,b=0.10 and p=0.04.It can be seen that the temperature increases with increasing values of the horizon radius and there is an inverse relation between the temperature and the mass of the BH.The increasing temperature w.r.t the horizon radius manifests that the BH shows thermodynamical stable behavior.The first law of thermodynamics for the topological dyonic dilaton BH can be expressed as [23–27],

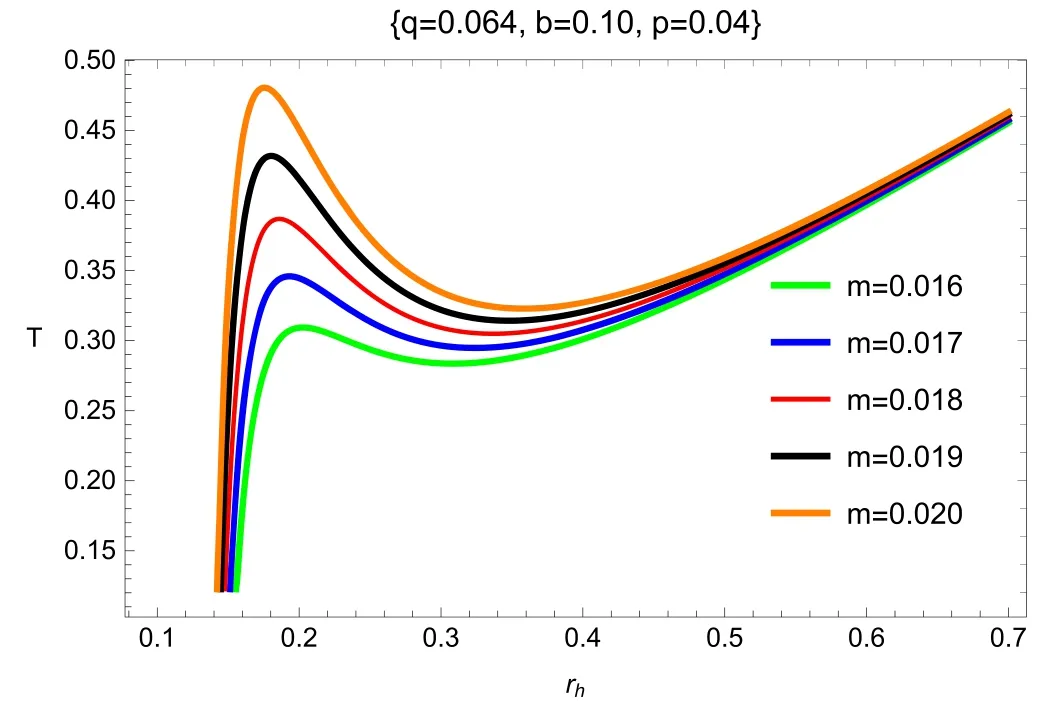
Figure 1.Plot of Hawking temperature T versus horizon radius rh of the topological dyonic dilaton BH.

where m,V,P,S and φ are the mass,volume,pressure,entropy and chemical potential,while P1,B1and K1are the conjugate variables.The thermodynamic volume and chemical potential of the BH can be obtained from the following relations:

respectively.Using the law of thermodynamics,the entropy of the BH becomes S=πr(r-2b).Another important model for the entropy is Rényi entropy,which is a valuable tool in the study of BH thermodynamics,offering a more refined understanding of the microstate structure and the quantum aspects of BH entropy beyond the leading Bekenstein–Hawking formula.Rényi entropy can explore the nuances of BH information and its connection to quantum gravity,and it has made a significant impact on the thermodynamics of BHs.It can be calculated as [28],

where λ represents a non-extensive variable with limitation-∞<λ<1.Rényi entropy turns into Bekenstein entropy for λ →0 and it yields a positive value for 0<λ<1.The mass of the BH in terms of Rényi entropy takes the following form:

Figures 2 and 3 manifest the plots of mass m in terms of Rényi entropy of the topological dyonic dilaton BH for different values of non-extensive Rényi parameter λ and dilaton field b,respectively.Figure 2 shows that the non-extensive Rényi parameter λ is directly related to the mass of the BH.The mass increases with increasing values of the Rényi parameter,which leads to the stable behavior of the BH.Figure 3 shows that the influence of dilaton field b on the mass of the BH is interesting because there exists a critical point in this plot.The mass of the BH decreases for increasing values of the dilaton field after the critical point,which results in instability of the BH.Using equation(10),one can rewrite the Hawking temperature of the BH in the form of Rényi entropy as follows:

Figure 2.Plot of mass m versus Rényi entropy SR for the topological dyonic dilaton BH.

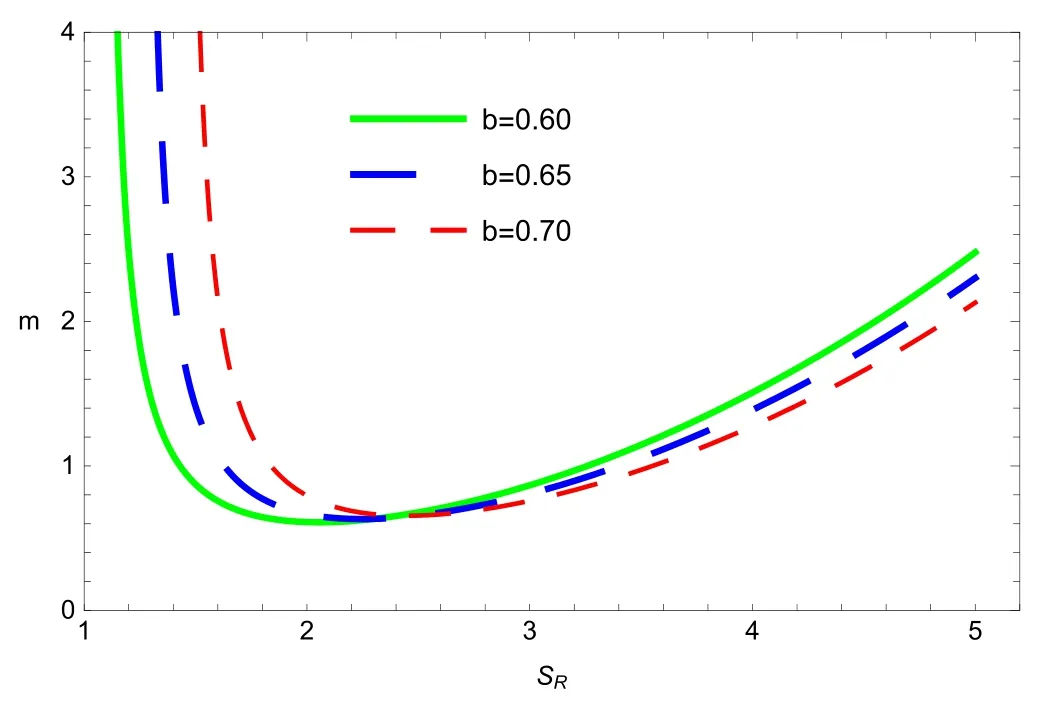
Figure 3.Plot of mass m versus Rényi entropy SR for the topological dyonic dilaton BH.

Using equation (9),the volume of the topological dyonic dilaton BH takes the following form:

From equations(9)and(10),the equation of state for the BH can be calculated (See appendix).The local stability of the BH can be studied using the specific heat capacity,which can be evaluated from the following relation [23,29,30]:

Using the relations of entropy and Hawking temperature,the specific heat of topological dyonic dilaton BH can be obtained (See appendix).Another important thermodynamic quantity is Gibbs free energy,which is used to study the global stability of the BH.It can be evaluated using the following relation [30,31]:

Utilizing the relations of mass,temperature and Rényi entropy,the Gibbs free energy in the form of Rényi entropy can be evaluated (See appendix).

Figure 4 manifests the pressure P in terms of Rényi entropy SRof topological dyonic dilaton BH for λ=0.001 and λ=0.99,respectively.Different curves correspond to different values of Hawking temperature of the BH.The red dashed curve corresponds to T>Tc,the green dashed curve curves correspond to TTc,i.e.red curves show that BHs are thermodynamically stable.Blue curves show that phase transitions occur at T=Tc,while green curves show that BHs are unstable with negative thermodynamic pressure.The negative range of pressure reduces for large Rényi parameter.The thermal local stability of the BHs can be studied from the heat capacity,the discontinuities of heat capacity yield phase transition.Moreover,positive and negative heat capacity provides local stability and instability of the BH,respectively.Figures 5 and 6 demonstrate the heat capacity in terms of Rényi entropy of the topological dyonic dilaton BH for different values of Rényi parameter and dilaton field,respectively.It can be observed that there exist divergence points in both plots,which show the phase transition points of the BH.We determine that for large BHs CP>0,which shows that a large topological dyonic dilaton BH is thermodynamically stable,while for small BHs CP<0,which represents the thermodynamic instability.By comparing both plots,it can be seen that Rényi parameter and dilaton field have a significant effect on the stability of the large BH,and the impact of both the parameters is negligible for the small BH.Figures 7 and 8 demonstrate the Gibbs free energy in terms of Rényi entropy of the topological dyonic dilaton BH for Rényi variable and dilaton field,respectively.In both plots,the Gibbs free energy is positive throughout the range,which manifests that the BH is globally stable.By comparing both plots,it can be seen that the increasing Rényi parameter decreases the overall range of the Gibbs free energy,while the Gibbs free energy increases with increasing values of the dilaton field.This means that both parameters have an important impact on the global stability of the BH.

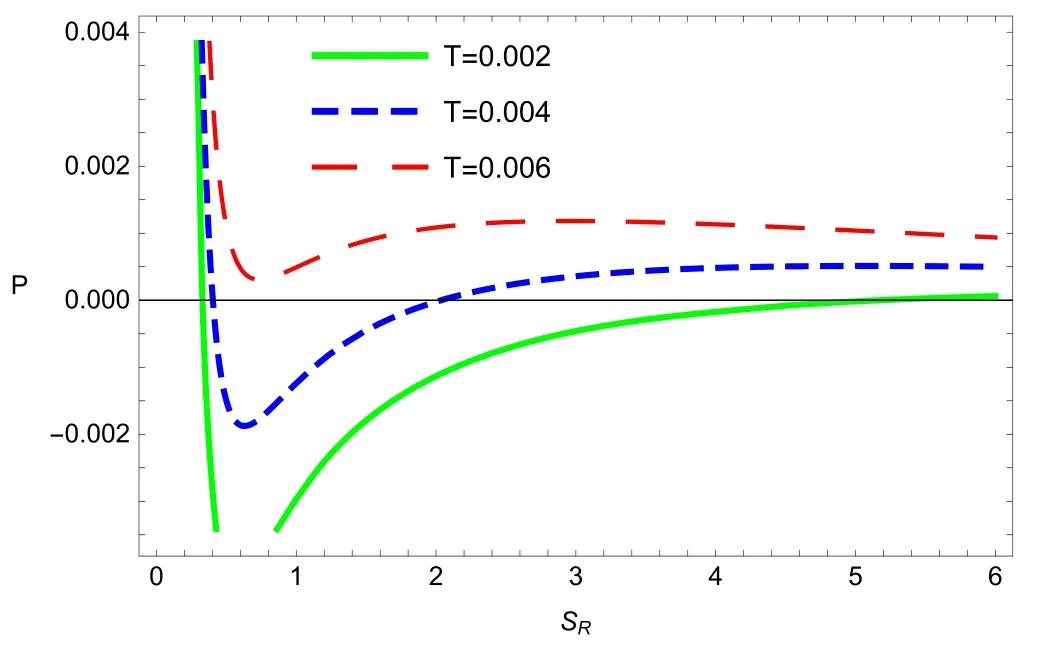
Figure 4.Plot of pressure P versus Rényi entropy SR for the topological dyonic dilaton BH with fixed values of critical temperature.

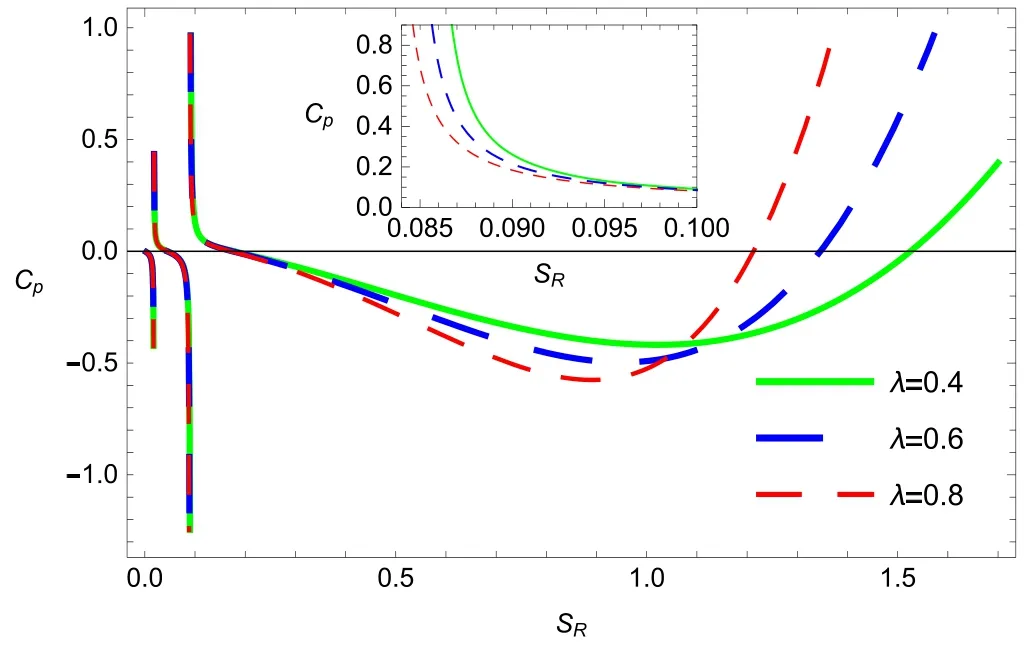
Figure 5.Plot of heat capacity Cp versus Rényi entropy SR of the topological dyonic dilaton BH.

Figure 6.Plot of heat capacity Cp versus Rényi entropy SR of the topological dyonic dilaton BH.

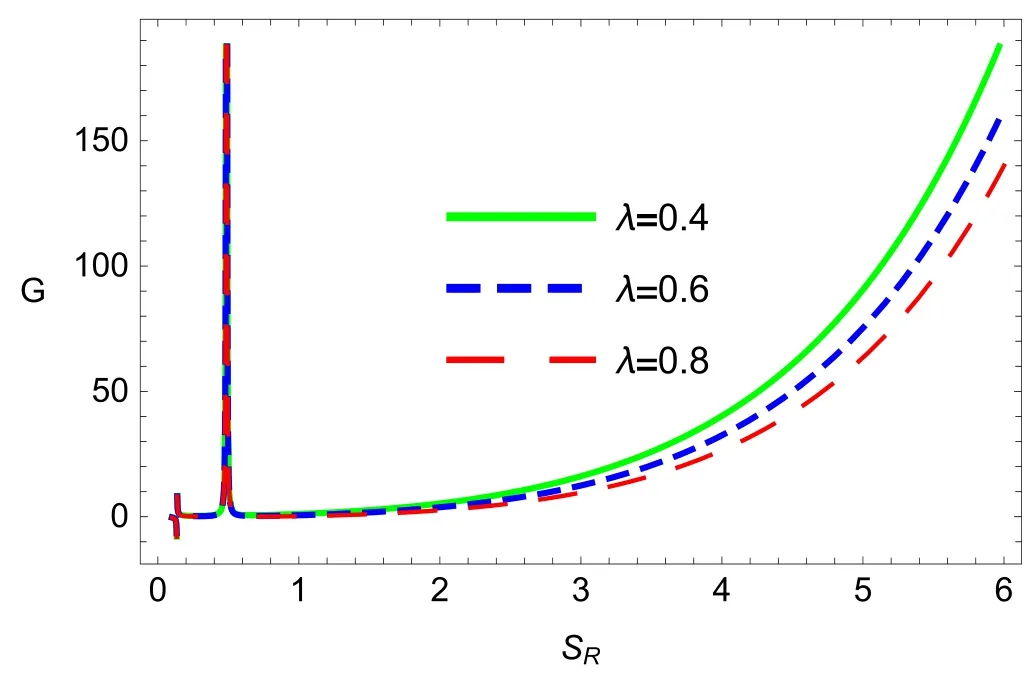
Figure 7.Plot of Gibbs free energy G versus Rényi entropy SR of the topological dyonic dilaton BH.

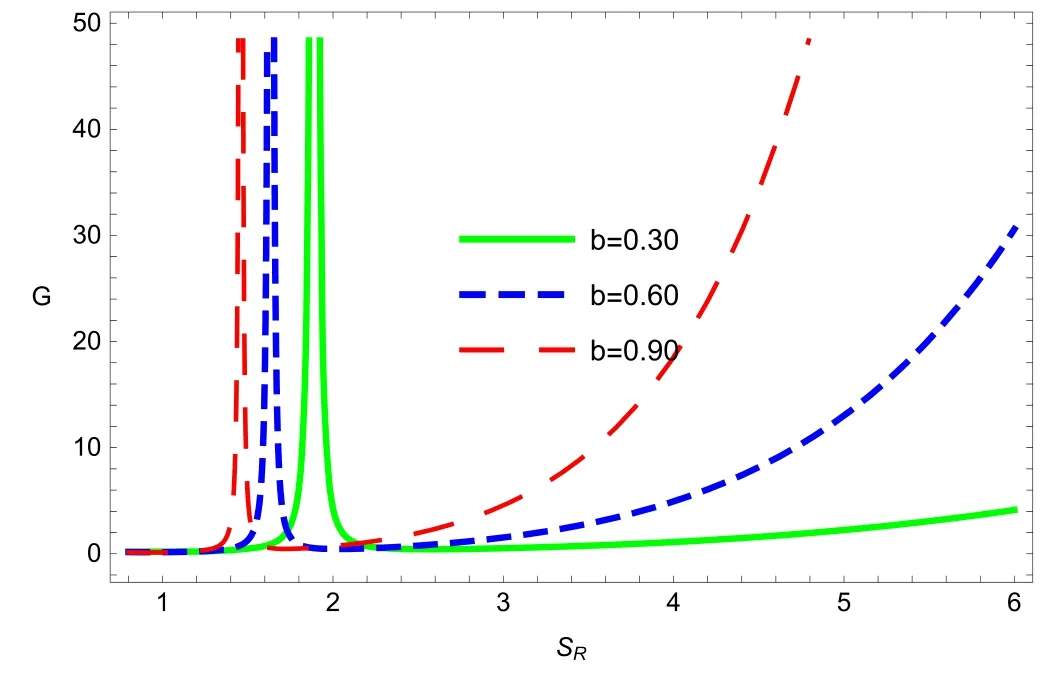
Figure 8.Plot of Gibbs free energy G versus Rényi entropy SR of the topological dyonic dilaton BH.

2.2.Thermal geometries of topological dyonic dilaton BHs

In this section,we use well-known models,such as Weinhold,Ruppeiner and Hendi Panahiyah Eslam Momennia(HPEM),to discuss the thermodynamical geometries of the topological dyonic dilaton BH.Basically,the thermodynamics geometry relates the thermodynamics to statistical mechanics in which a suitable metric space is decisive in the equilibrium state of a thermodynamic system.We first discuss the thermal stability of the topological dyonic dilaton BH using the heat capacity of the BH.The positive/negative heat capacity yields stability/instability of the BH regardless of the values of parameters in this theory.The relations for mass and Hawking temperature of the BH in terms of entropy take the following form:

The divergence points of heat capacity yield the phase transition point.The relation for heat capacity can be obtained from the following:

In our analysis,we focus on the geometric mass to study the geometries.The relation for Weinhold geometry in terms of mass is given by [32],

The metric form of the topological dyonic dilaton BH takes the following form:

whose matrix form is given by,

Using the above relation,the scalar curvature of Weinhold metric (RW) for the topological dyonic dilaton BH can be calculated as,

Figure 9 manifests the scalar curvature of Weinhold metric(RW) and specific heat of the topological dyonic dilaton BH to study the phase transition.It can be seen that the divergence points of the scalar curvature coincide with the zero of specific heat,which represents the phase transition point.Moreover,the variation in singular points of scalar curvature is consistent with the divergences of figures 7 and 8,which also confirms our analysis.Ruppeiner geometry is another important model that is conformal to the Weinhold geometry and it is defined as [32],

Figure 9.Plot of the heat capacity and curvature scalar for Weinhold metric of the topological dyonic dilaton BH.

Using the thermodynamic quantities of the topological dyonic dilaton BH in the above equation,the curvature for Ruppeiner geometry turns out to be the following:

Figure 10 manifests the scalar curvature of Ruppeiner geometry R(Rup)and specific heat of the topological dyonic dilaton BH to study the phase transition.Similar behavior of the plots is observed to that discussed for scalar curvature of Weinhold metric,which confirms our finding.Finally,we study the HPEM geometry and the metric for HPEM geometry is defined as[32],

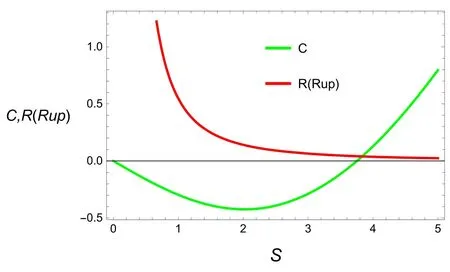
Figure 10.Plot of the heat capacity and curvature scalar for Ruppenier geometry of the topological dyonic dilaton BH.

The scalar curvature of the topological dyonic dilaton BH for HPEM geometry takes the following form:

Figure 11 manifests the scalar curvature of HPEM geometry and specific heat of the topological dyonic dilaton BH.Our analysis reveals that the scalar curvature of the topological dyonic dilaton BH for the HPEM has no singular point,which indicates that HPEM metric has no physical information.

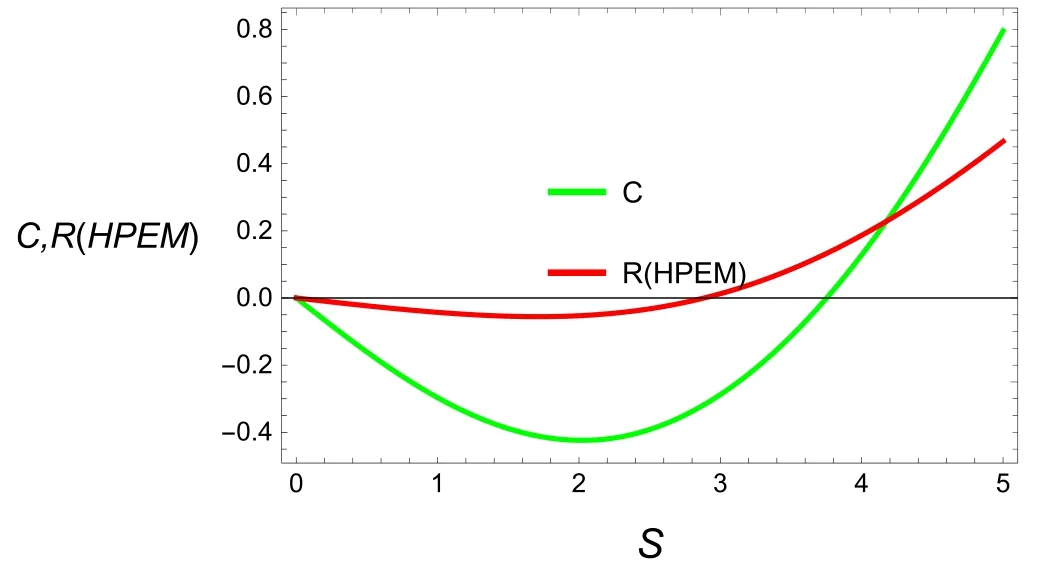
Figure 11.Plot of the heat capacity and curvature scalar for HPEM geometry of the topological dyonic dilaton BH.

Figure 12.Numerical plot of the mass of the topological dyonic dilaton BH w.r.t lifetime t with non-dilaton field y=0 (corresponding to b=0).We set l=10,l=15 and l=20 from left to right.

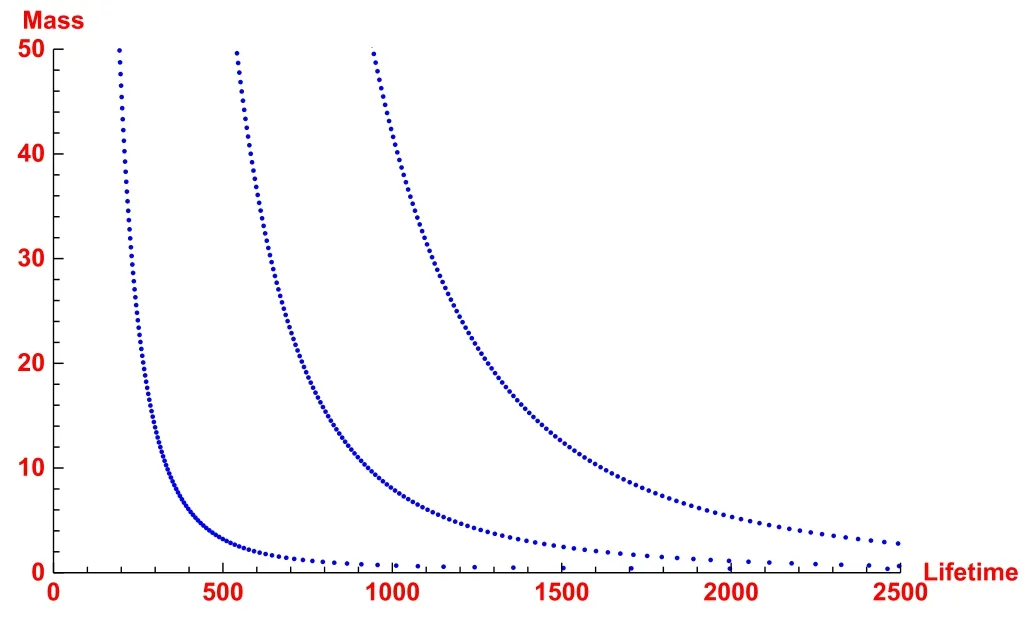
Figure 13.Numerical plot of the mass of the topological dyonic dilaton BH versus evaporation time t with dilaton field y=10(corresponding to b=10).We set l=10,l=15 and l=20 from left to right.

2.3.Hawking evaporation of topological dyonic dilaton BHs

According to Hawking,the BH emits radiation,which leads to the decrease in mass of the BH w.r.t its lifetime.Geometrical optics show that the ejected radiation particles move along the null geodesics.Thus,the normalized affine parameter λ yields the geodesic equation along the orient angular coordinate,which is given by [33],

for all r>rh.According to Boltzmann's law the ejection rate of radiation is defined as [33],

Here,ξ(x,y) is a very lengthy expression that is not worth mentioning here.Integrating the expression from ∞toxmin=0for fixed y,we evaluate the BH lifetime.We manifest the temperature of the topological dyonic dilaton BH with respect to rhfor different cases in figure 1.Temperature plays a significant role in the Hawking evaporation process because it has high order.Figures 12 and 13 manifest the numeric plots of the mass of the topological dyonic dilaton BH versus its time for evaporation t for b=0 and b=10.In both plots,all three curves are l=10,l=15 and l=20 from left to right.For b=0,singularity occurs when the BH temperature becomes divergent for large horizon radius [34].The minimum horizon radius gives minimum mass of the BH,which quickly evaporates.On the other hand,for b=10,initially the BH reduces mass in a short time period and later the process slows down for a very small mass BH.This leads to a lengthy time for evaporation of the BH and satisfies the third law of BH thermodynamics.There is the possibility that the BH turns into a remanent,which can provide a breakthrough to resolve the information loss paradox [35].Amongst our important findings,we determine that the BH without a dilaton field (b=0) evaporates far more quickly compared to the dilaton field BH (b=10).

3.Conclusion

BH thermodynamics provides a remarkable connection between gravity and the thermodynamical quantities of the BH.This connection suggests that gravity has a thermodynamic origin,and it has profound implications for analyzing time,space and fundamental laws of the Universe.In this study,we have considered a topological dyonic dilaton BH in AdS space and studied some important thermodynamic aspects of BHs.We have evaluated the relations of pressure,heat capacity and Gibbs free energy using Rényi entropy.We have determined that Rényi parameter and dilation field of the BH play an important role in the stability of the BH.We established that for large BHs CP>0,which shows that large topological dyonic dilaton BHs are thermodynamically stable,while for small BHs CP<0,which represents the thermodynamic instability.We used Weinhold,Ruppeiner and HPEM geometries to find the scalar curvature of a topological dyonic dilaton BH in AdS space.We observed that the discontinuous points of the scalar curvature coincide with the zero of heat capacity,which represents the phase transition point.Moreover,the variation in singular points of scalar curvature are consistent with the divergences of Figures 7 and 8,which also confirms our analysis.Finally,in order to study the Hawking evaporation of the BH,we plotted the numerical results of mass m of the topological dyonic dilaton BH versus its lifetime t and observed that the BH without a dilaton field evaporates more quickly compared to the BH with a dilation field.

Acknowledgments

This project was supported by the National Natural Science Foundation of China (Grant No.11 975 145).The authors thank the reviewers for their comments on this paper.

Appendix