Black hole evaporation and its remnants with the generalized uncertainty principle including a linear term

Bo Yu and Zheng-wen Long

College of Physics,Guizhou University,Guiyang,550025,China

Abstract In recent years,researchers have investigated the evaporation of Schwarzschild black holes using various forms of the generalized uncertainty principle(GUP),metric quantum correction,and noncommutative geometry,respectively.However,there are differences between the GUP correction and the other two methods in terms of describing the later stages of black hole evaporation.Furthermore,some studies argue that the GUP with a negative parameter cannot effectively correct black hole evaporation,while others contend that the positivity or negativity of the GUP parameters should not affect the correction results.Taking the above into consideration,we reconsider black hole evaporation with the generalized uncertainty principle including a linear term (LGUP),and examine the case of negative parameters.The results indicate that the evaporation behavior of both Schwarzschild black holes and Reissner–Nordström black holes,under LGUP correction,is consistent with the results of metric quantum correction and non-commutative geometry.Additionally,the negative parameter LGUP can also effectively correct for black hole evaporation.

Keywords: black hole evaporation,generalized uncertainty principle,negative parameter

1.Introduction

In the 1930s,with the emergence of quantum field theory,attention was drawn to the possible existence of a minimum length.By the mid-1970s,the study of black hole thermodynamics [1,2] provided an important theoretical basis for widely recognizing the possible existence of a minimum observable length.Later,with rapid developments in string theory [3,4],black hole physics [5],non-commutative geometry [6],and other theories,this perspective became deeply ingrained in people’s minds.People have also modified the traditional Heisenberg uncertainty principle,which contradicts the existence of a minimum length,and proposed the generalized uncertainty principle (GUP).After its proposal,the GUP was quickly applied to various areas of physics such as gravitational corrections for quantum systems [7–10],corrections to the thermodynamics of black holes [11–17],and cosmology [18,19].Additionally,the positive and negative GUP parameters have sparked numerous discussions:rainbow gravity corrections to the black hole information flux and Hawking radiation sparsity [20],the modification of special relativity [21],and the negative parameter of the GUP to recover the Chandrasekhar’s limit [22],etc.,argue that the negative parameter is applicable to a specific model.However,others contend that the existence of the minimum length should be universal,meaning that both positive and negative GUP parameters should not be limited by a specific model[23,24].

In 1975,Hawking proposed Hawking radiation in [25],which demonstrates that black holes not only absorb objects but also emit energy outward.However,during this process,the temperature of the black hole becomes infinitely high.Later on,GUP was developed and applied to black hole thermodynamics,indicating that instead of being infinite the temperature reaches a non-zero finite value [26].Although GUP can correct for Hawking radiation,the obtained results still differ from those of metric quantum correction [27] and non-commutative geometry [28],which also reflect the minimum lengths.In recent years,researchers have made continuous efforts and proposed several revised models,such as EUP [29],EGUP [30,31],LGUP [32,33],in order to achieve a consensus.

The LGUP proposed in literature [33],which is consistent with string theory,double special relativity,and black hole physics,has caught our attention among the various options available.Although the literature [34] has calculated black hole evaporation using LGUP,it does not provide thermodynamic images.Therefore,based on the results of the literature [34],we have drawn corresponding images.However,we have discovered that its description of black hole evaporation is inaccurate.Furthermore,recent literature [35]has identified deficiencies in the current method used to calculate the corrected thermodynamic quantities of black holes[26,36],and proposed an improved method.Literature [37]successfully reproduced GUP from the modified entropy obtained by this improved method and demonstrated its reasonability and effectiveness.Inspired by these studies,we have investigated the thermodynamic properties of black holes under LGUP using this improved method and plotted thermodynamic images for comparison with the existing studies while considering the negative parameter problem of LGUP.

The structure of this paper is as follows:in section 2,we provide a brief introduction to LGUP.In section 3,we calculate the temperature,entropy,heat capacity,evaporation rate,and sparsity of Hawking’s radiation as functions of evaporated mass for LGUP corrections with positive and negative parameters.We also plot thermodynamic images to compare with existing studies.In section 4,we calculate the functions of each thermodynamic quantity and the mass of the RN black hole with both positive and negative parameters of LGUP.Furthermore,we investigate the influence of charge Q on the thermodynamic properties of RN black holes.Finally,our findings are summarized in section 5.

2.The generalized uncertainty principle including a linear term (LGUP)

Firstly,the line element of Schwarzschild black hole spacetime is given.

where G is the gravitational constant,M is the mass of the Schwarzschild black hole,and r is the distance to its center.

is Schwarzschild radius.

The literature [33] presents the generalized uncertainty principle including a linear term (LGUP) as follows:

Because the right-hand part of equation (6) can be simplified into the Heisenberg uncertainty principle as α →0,while the left-hand part cannot,we take:

3.Thermodynamics of a Schwarzschild black hole

3.1.The functions of each thermodynamic quantity and the mass of a black hole

Literature [25] has shown that black holes possess thermodynamic properties,indicating the existence of a relationship among their mass,energy,entropy,and temperature.Among these properties,mass is the most fundamental and crucial one for a black hole as it determines its ability to attract surrounding matter,the greater the mass,the stronger its gravitational pull.Furthermore,by comparing the first law of black hole thermod ynamics dM=dA+ΩdJ+VdQwith the first law of thermodynamics for a rotating object dU=TdS+ΩdJ+VdQ,it can be observed that the surface gravity κ corresponds to the temperature T,the area of the event horizon A corresponds to the entropy S,and the mass M of the black hole corresponds to the internal energy U of a thermodynamic system.The mass of a black hole is closely related to its energy.According to the mass-energy relation E=mc2,changes in mass correspond to changes in energy.Therefore,the mass of a black hole can be considered as its thermodynamic energy [38].

We associate the mass of the black hole with other thermodynamic quantities in order to describe the evaporation behavior of the black hole accurately.First,we calculate the functions of temperature,entropy,heat capacity and other thermodynamic quantities as well as the mass of the black hole respectively.

Take the minimum value of equation (7):

and use the subscript L to represent the physical quantities of the LGUP correction calculated by this method.

Under the geometric background near the horizon of a Schwarzschild black hole,the position uncertainty of particles should be proportional to the Schwarzschild radius[39],then:

where μ is a scale factor rHis the Schwarzschild radius.

Therefore,

According to the change in energy when a black hole absorbs or releases particles,we have:

Substituting equation (15) into equation (14) gives:

According to the definition of differential,an approximate modified differential area dALcan be obtained:

Substituting equations (10),(11) and (13) into equation (17) gives:

According to Bekenstein–Hawking area lawthe differential expression of entropy can be obtained:

Substitute equation (19) into the expression the corrected temperature TLcan be obtained:

Then we consider α →0 situation,at this time

find the simplified temperature TLis the same as the semiclassical Hawking temperature.At the same time,since there is no scale factor μ in the temperature expression obtained when α →0,regardless of the value of μ,the temperature expression can be simplified to the semi-classical Hawking temperature without considering quantum correction.For convenience,according to [34] take:

Integrate equation (24),an expression SLfor entropy in logarithmic form is obtained:

We observe that there are logarithmic terms in the expression of entropy,which is consistent with numerous studies [11,13,26,29,34–36,39].

By definition,the heat capacity of a black hole iswhich reflects the relationship between changes in mass(energy) and changes in temperature.From the perspective of thermal balance,positive and negative heat capacity reflect the stability of the thermodynamic system.When the heat capacity is negative,the thermodynamic system is unstable: a black hole loses mass(energy) through the process of evaporation in an attempt to cool down.However,during this process,due to the negative heat capacity,the temperature of the black hole increases,leading to further disruption of the thermal balance of the system.When the heat capacity is zero,dM/dT becomes zero,indicating that the black hole mass(energy) no longer changes with temperature and a remnant remains after the evaporation of the black hole.When the heat capacity is positive,it corresponds to the stability of the thermodynamic system: as the black hole undergoes evaporation and loses mass (energy),its temperature also decreases,leading the thermodynamic system towards thermal equilibrium.

The derivative of equation (23) with respect to M is

The thermal evolution of an asymptotically flat Schwarzschild black hole is:

where a is the radiation constant,essentially σ is the area (in geometrical optics approximation,it is the photon capture cross section σ=27πM2),ρ is a gray body factor.Because we just want to make a general and qualitative analysis of evolution,we will consider a simple case [40]:

Substitute equation (23) into equation (29) to get the evaporation ratefor:

In addition,studies have shown that the sparsity of Hawking radiation will affect the evaporation of black holes[40,41].Therefore,we calculate the dimensionless ratio η that characterizes sparsity with the LGUP correction:

In order to facilitate the subsequent generation of thermodynamic images and compare our results with those of previous studies,we perform an equivalent transformation on the relationship between thermodynamic quantity and mass described in[34],using the subscript E to represent the calculated physical quantities.Take the expression for temperature in [34]:

Therefore,entropy,heat capacity,evaporation rate,and η are respectively:

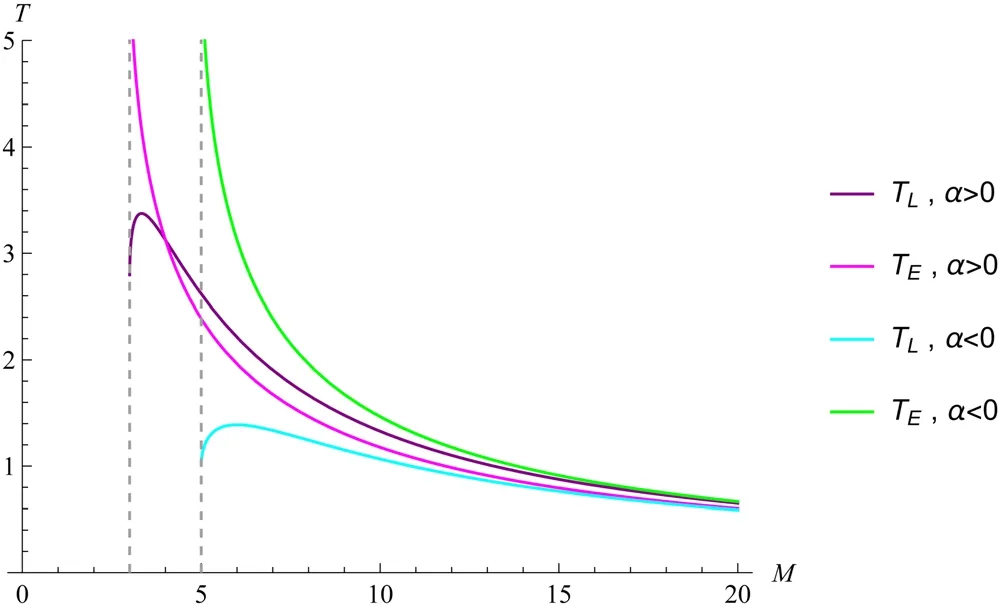
Figure 1.The relationship between black hole temperature and mass is given by equation (23) and equation (34).

3.2.Comparison and analysis

To better reflect the variation of each thermodynamic quantity with the black hole mass,we draw thermodynamic images and set G=c=ħ=kB=π=1 in the drawings.In addition,several studies have indicated that the positive or negative values of parameter α in the generalized uncertainty principle has an impact on black hole evaporation [40].Although,the current research mostly focuses on α>0[30,32,41,42],but reference[43]indicates that α<0 can be obtained through the deformed Schwarzschild metric.Reference [22] also shows that α<0 is meaningful in certain cases.Therefore,we have also considered the case of α<0 and taken∣α∣=8.We plotted thermodynamic images to compare this study with the existing study,for both cases of α>0 and α<0.

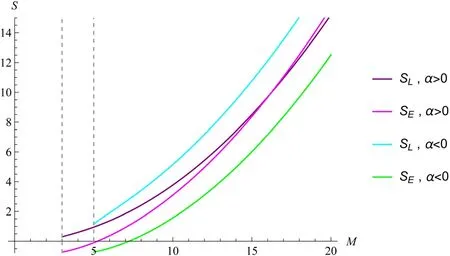
Figure 2.The relationship between black hole entropy and mass is given by equation (25) and equation (35).

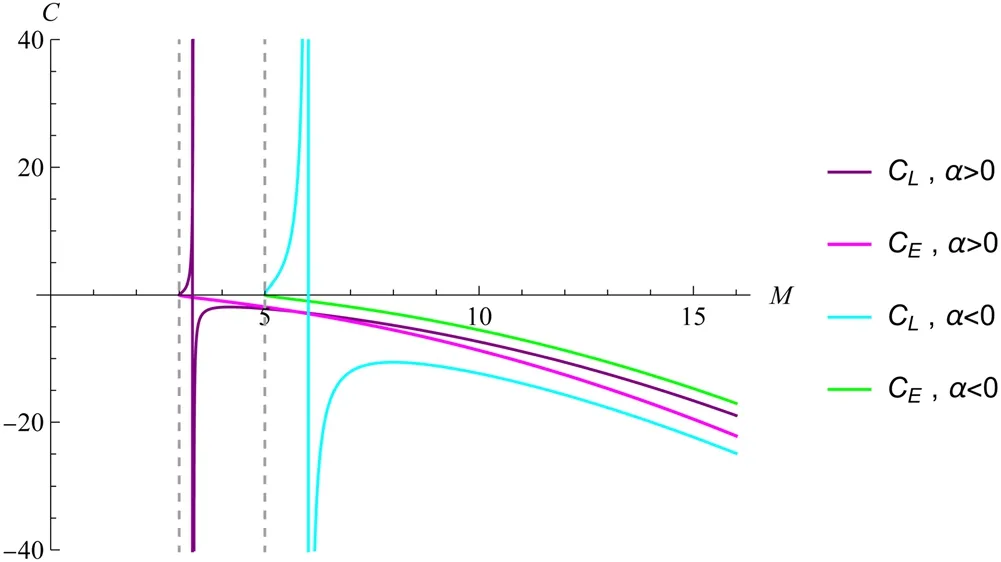
Figure 3.The relationship between black hole heat capacity and mass is given by equation (27) and equation (36).

In figure 1,it can be observed that the remnants were left after the evaporation of the black hole.When α>0,both the temperature TLcalculated in this study and the temperature TEcalculated from the existing study increase as a result of black hole evaporation within a certain mass range.When the mass of the black hole approaches the residual mass,their behaviors begin to differ:TLbegins to decline after reaching a maximum,and TEcontinues to rise until it reaches its peak.Both TLand TEeventually converge to non-zero finite temperatures,which resolves the issue of temperature divergence in the later stages of black hole evaporation[44].However,an increasing number of studies have demonstrated that the temperature changes during black hole evaporation should align with the findings of this study:the temperature begins to decrease as it approaches residual mass rather than maintaining a constant upward trend[27,28].When α<0,unlike the previous study [35],the quantum correction does not fail.The image of negative α maintains the same trend as that of positive α,and negative α increases the residual mass of black hole evaporation.

In figure 2,both SLand SEtend to decrease as M decreases.The difference is that SLeventually becomes a non-zero finite positive value,which is consistent with the research results [45].However,as M decreases,SEgradually approaches zero and eventually becomes a negative value,but negative entropy holds no physical significance.The area of a black hole’s event horizon cannot have a negative value,and acknowledging the correctness of Bekenstein–Hawking area law implies that the entropy of a black hole cannot be negative either.Therefore,we believe that the changing trend of SLis more convincing than that of SE.

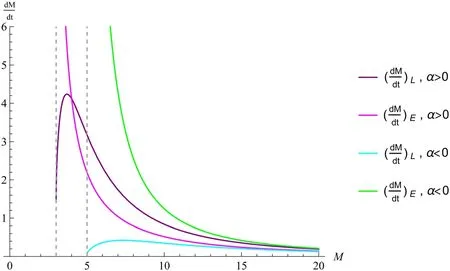
Figure 4.The relationship between black hole evaporation rate and mass is given by equation (30) and equation (37).

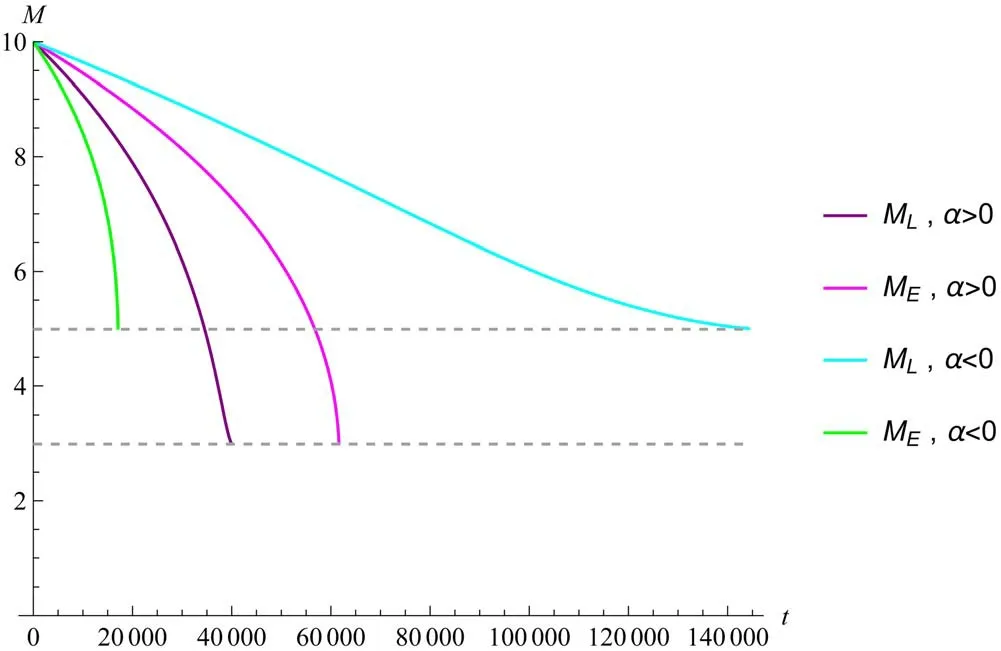
Figure 5.The relationship between black hole mass and evaporation time is given by equation (30) and equation (37).

In figure 3,the heat capacity CLis divided into positive and negative parts,and it diverges when the temperature reaches its peak.In the initial phase of evaporation,CLstarts with a negative value and gradually converges towards zero as M decreases;in the subsequent stage of evaporation,CLis positive and rapidly approaches zero as M further decreases.The change in CLdirectly corresponds to the change in temperature TL,and literature [29] also indicates that the symbol for heat capacity changes with varying temperatures.CEcontinues to rise towards evaporation and remains negative throughout the process.The heat capacity symbol serves as an indicator of the thermodynamic system’s stability.The presence of a negative heat capacity indicates the thermodynamic system’s instability,while a positive heat capacity signifies its stability[46].When the mass of a black hole approaches the residual mass,a positive heat capacity is more favorable for the formation of remnants of black holes.

In figure 4,(dM/dt)Linitially increases as M decreases.The evaporation of black holes is suppressed as M approaches the residual mass [47],leading to a decrease in (dM/dt)L.(dM/dt)Econtinues to increase throughout the entire evaporation process.For an evaporation process,it is often more reasonable for the evaporation rate to gradually decline in the later period until reaching the residual mass,rather than continuously rising and abruptly stopping.In addition,the decreasing evaporation rate is also more appropriate for describing black hole remnants that require a significant amount of time,or even an infinite amount of time,to be radiated away [48,49].

In figure 5,the decline trend of MLgradually slows down over time,indicating a decreasing rate of decay for the black hole mass.This corresponds to the gradual decrease in evaporation rate during the late stages of evaporation.The change trend of MEis opposite to that of ML,and the rate of decay in black hole mass accelerates progressively,ultimately expediting the entire evaporation process.

In figure 6,ηLgradually increases as M decreases,while ηEgradually decreases as M decreases.The references [50]and [51] demonstrate that an increase in sparsity η will slow down the frequency of radiation.By combining the image of η with other thermodynamic images,it can be observed that ηLgradually increases,sparsity increases,evaporation rate decreases,and the mass attenuation of the black hole slows down.On the other hand,ηEgradually decreases,sparsity decreases,evaporation rate increases,and black hole mass decay becomes more rapid.

In summary,we find that the literature[34]describes the late stage of evaporation as having high temperatures,high rates of evaporation,negative entropy,negative heat capacity,and ultimately an extremely unstable black hole remnant,which is inconsistent with much of the current research.Our research suggests that the later stage of evaporation is characterized by low temperature,low rates of evaporation,positive entropy,and positive heat capacity and ultimately results in the formation of a relatively stable black hole remnant.Furthermore,literature [52] argues that entropy should be zero at the end of evaporation.However,since the entropy we obtained is a positive value,we believe that evaporation is highly likely to continue under certain conditions.If evaporation continues,the decreasing rate of evaporation will result in a longer time required to evaporate the remaining mass.Literature [53] believed that when the evaporation reaches the Planck scale,the black hole will tunnel into the white hole,and then it will take a longer time to complete evaporation.Our research findings offer a suitable depiction of this phenomenon.Our images are consistent with those obtained from calculations of metric quantum correction[27] and non-commutative geometry [28].

For α<0,the quantum correction remains valid,and negative α also increases the black hole’s residual mass compared to positive α.

In addition,it has been demonstrated that the linear term in LGUP impacts the residual mass of the black hole [54].Therefore,to investigate the influence of linear terms in LGUP on the residual mass of the black hole,we calculate the residual mass under GUP and LGUP corrections when α>0.According to the definition of heat capacity,when the black hole ceases radiation,its heat capacity should be zero.Therefore,the residual mass can be determined by setting C=0.By utilizing equation (27) and the heat capacity expression provided in literature [35],we can obtain:

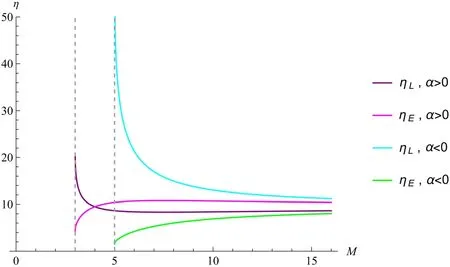
Figure 6.The relationship between black hole mass and η is given by equation (32) and equation (38).

where Mp=c=π=1,α=8.

Therefore,the presence of a linear term(α>0)in LGUP leads to an increase in the residual mass of the black hole,which is consistent with the discovery [54].Furthermore,α<0 further enhances the residual mass,building upon the foundation of α>0.

The literature [52] suggests that the parameter α of the generalized uncertainty principle has an impact on the process of black hole evaporation.Therefore,we also plot the temperature and evaporation rate for various values of parameter α.

Figure 7 and figure 8 above demonstrate that a decrease in ∣α∣leads to an increase in the peak value of temperature and evaporation rate,while simultaneously reducing the residual mass of the black hole.These findings are consistent with those reported in the existing literature[52].The smaller the value of ∣α∣,which leads to an increased evaporation rate,the higher the temperature of the black hole and the lesser amount of residual mass that remains.However,the impact of parameter α on temperature,evaporation rate,and residual mass is limited.First,∣α∣cannot gradually decrease to zero;otherwise,the generalized uncertainty principle will degenerate into the traditional Heisenbergs uncertainty principle.Similarly,∣α∣cannot indefinitely increase to reduce the peak value of black hole temperature and evaporation rate while simultaneously increasing the residual mass.The literature[54]suggests that an upper bound for the parameter ∣α∣can be determined by setting the maximum mass of the black hole.Similarly,we can set the mass of a black hole and then use the expression (ΔpL)minto ensure that1thereby obtaining the range of values for the parameter α.

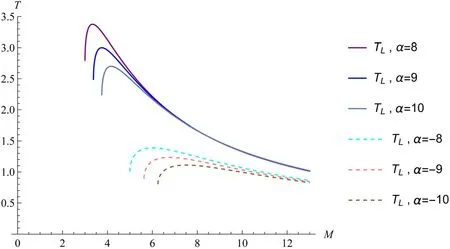
Figure 7.The figure illustrates the correlation between black hole temperature and mass,while considering different values of parameter α.

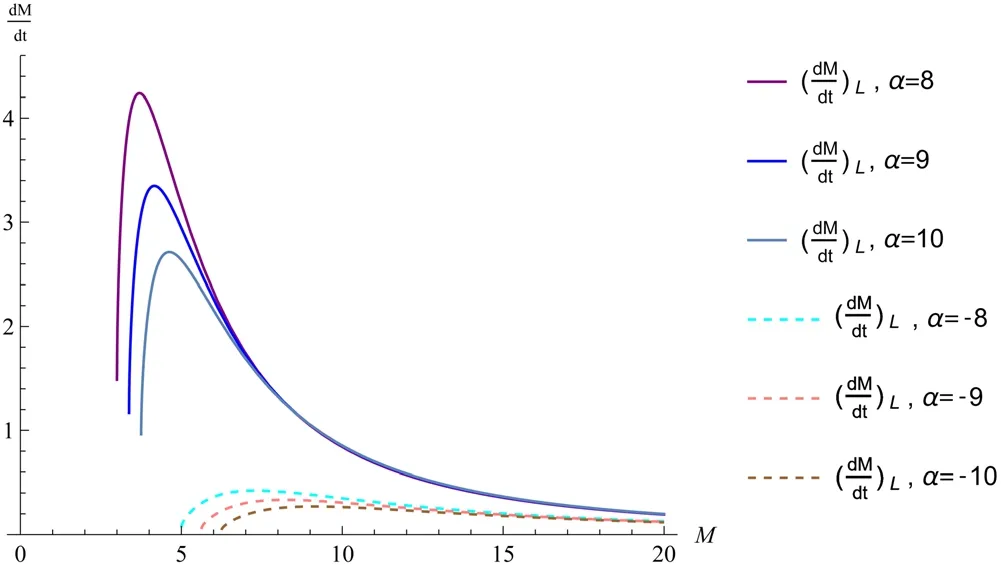
Figure 8.The figure illustrates the correlation between black hole evaporation rate and mass,while considering different values of parameter α.

Figure 9.The relationship between the temperature and mass of an RN black hole is given by equation (59).

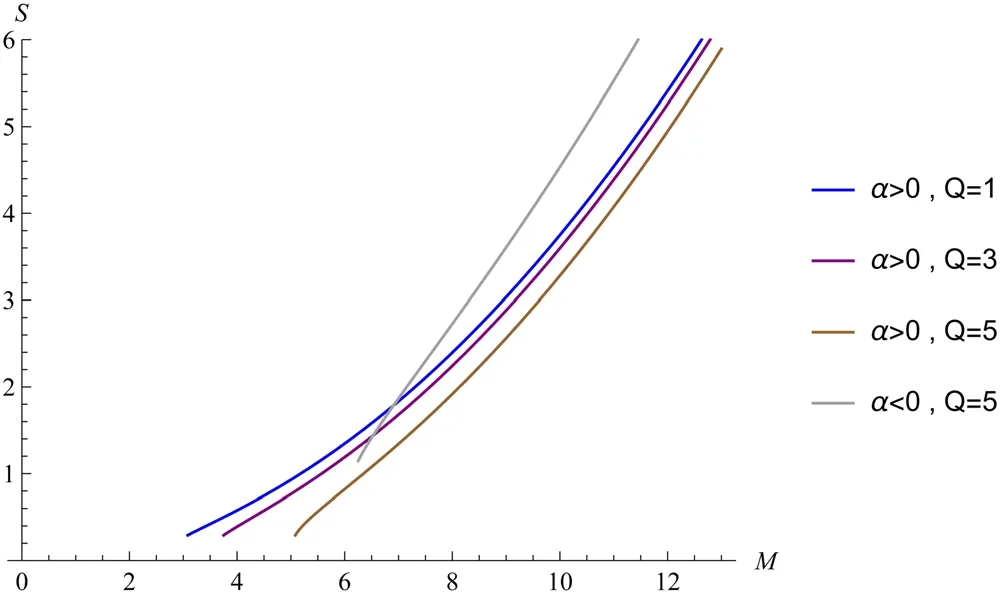
Figure 10.Equation (60) is integrated to obtain the relationship between the entropy and mass of an RN black hole.

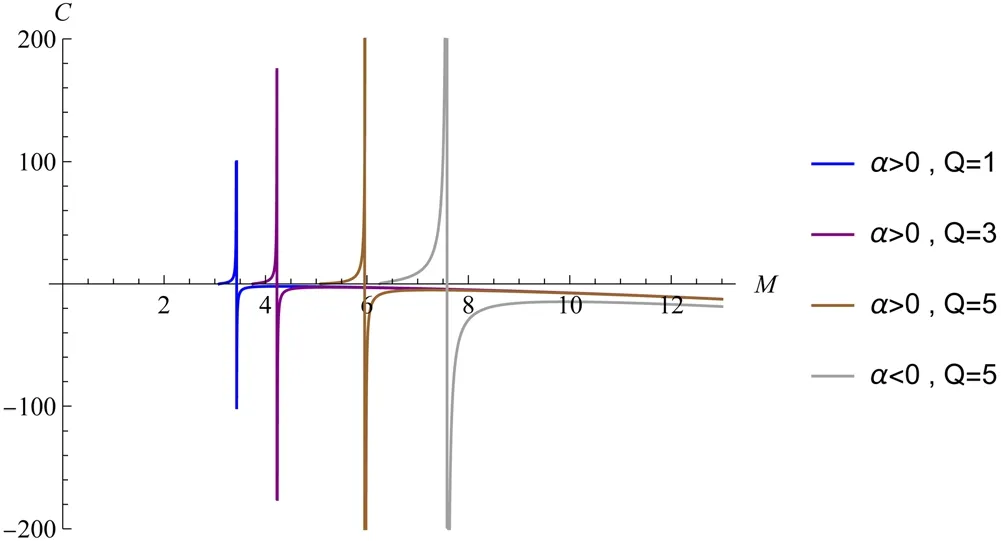
Figure 11.The relationship between the heat capacity and mass of an RN black hole is given by equation (62).

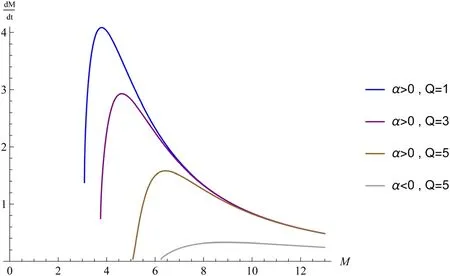
Figure 12.The relationship between the evaporation rate and mass of an RN black hole is given by equation (63).

4.Thermodynamics of a Reissner–Nordström black hole

In this part,we will use the same method as in section 3 to calculate the function of each thermodynamic quantity and the mass of a Reissner–Nordström(RN)black hole,and study the influence of charge Q on the thermodynamic properties of an RN black hole.The line element of an RN black hole in a natural system of units is:

where M and Q are the mass and charge of the RN black hole[55].

are the radius of the inner and outer event horizon of the RN black hole.

Considering that when Q=0,r±should degenerate to the Schwarzschild radius,so take the outer event horizon radiusTo ensure the completeness of the calculation,the outer event horizon radius of the RN black hole is restored to the ordinary system of units,then:

where γ is a scale factor.

Also,take the minimum value of equation (7):

and use the subscript RN to represent the physical quantities of the RN black hole.

Substituting equation (45) into equation (46):

The area of the horizon obtained from A=4πr2is:

where ΔM ≃cΔp is used in the calculation.

According to the definition of differential:

Substituting equation (46),equation (48) and equation (50) into equation (52):

When α=0,Q ≠0:

is the same semi-classical Hawking temperature as the RN black hole.

When α=0,Q=0:

degenerates to the semi-classical Hawking temperature of the Schwarzschild black hole.At the same time,because the value of the scale factor γ does not affect the final degradation ofto the semi-classical Hawking temperature,in order to maintain consistency with the literature [56],we take:

Next,we set G=c=ħ=kB=π=1 and∣α∣=8and plot thermodynamic images of an RN black hole with different Q values.

Figures 9–12 clearly demonstrate that,as the charge value Q increases for the same parameter α,both the temperature and evaporation rate curves slow down and their peaks decrease.The larger the value of Q,the greater the residual mass of the RN black hole and the higher the extreme values of both positive and negative heat capacities.When the mass is the same,a higher Q value corresponds to a lower entropy value.The pattern of variation in the thermodynamic quantity of the RN black hole with Q that we obtained is consistent with the literature[56].The difference with the literature[56]is that: when comparing it to the image of the Schwarzschild black hole,we observe that in our study,the thermodynamic images of both black holes are similar and consistent with metric quantum correction [27] and non-commutative geometry [28].While the Schwarzschild black hole in the late stages of evaporation,as described in the literature [56],still has a high temperature and negative heat capacity.

5.Conclusion

In this paper,we successively calculate the functions of thermodynamic quantities and masses for a Schwarzschild black hole and an RN black hole with the LGUP modification.We then plot the thermodynamic graphics to compare them with previous studies.Our findings are as follows:

1.The scale factors μ and γ,which are introduced in the calculation of particle position uncertainty,no longer need to take a fixed value.Especially for RN black holes,γ instead ofThis not only simplifies the calculation but also yields the same result as

2.For α<0,the quantum correction remains valid,satisfying the requirement that the quantum correction should not be affected by specific conditions.Compared to positive α,negative α increases the extreme value of residual mass,entropy,and heat capacity of the black hole while decreasing the peak value of temperature and evaporation rate.If evaporation continues,a negative α will prolong the time required for complete evaporation.

3.The evaporation of the black hole is influenced by the value of parameter α.The smaller the ∣α∣,which leads to a faster rate of evaporation,the higher the temperature of the black hole and the smaller the residual mass remaining after its evaporation.However,it should be noted that there exist limitations on the range of values for parameter α.

4.The thermodynamic images suggest that an increase in sparsity η results in a deceleration of evaporation during the later stages.The reduced evaporation rate and positive heat capacity enable us to obtain a relatively stable remnant of the black hole.The non-zero entropy implies a high likelihood of continued evaporation,and if this occurs,the black hole will tunnel into the white hole and then complete the evaporation after a longer period of time.

To sum up,LGUP increases the residual mass of the black hole and is better suited for describing the remnants of a black hole that takes a long time,or even an infinite amount of time,to be radiated away.Both positive and negative parameters of LGUP can effectively correct the black hole evaporation,allowing the quantum correction to be unrestricted by a specific model.Furthermore,the thermodynamic images we obtained are consistent with those obtained through metric quantum correction and non-commutative geometry as well.At the end of the manuscript,we hope that further research can be conducted on the negative parameters of LGUP in the future.

Acknowledgments

This study is supported by the National Natural Science Foundation of China (Grant No.12265007).