The modeling non-sequential double ionization of helium atom under highintensity femtosecond laser pulses with shielding charge approximation

Marjan Zakaviand Mohammad Sabaeian,2,∗

1 Department of Physics,Faculty of Science,Shahid Chamran University of Ahvaz,Iran

2 Center for Research on Laser and Plasma,Shahid Chamran University of Ahvaz,Iran

Abstract In this study,we successfully extracted the‘knee structure’for non-sequential double ionization(NSDI) in the helium atom.To achieve this,for the first time,we solved the time-dependent Schrödinger equation in three dimensions for the helium atom,utilizing the shielding charge approximation.Our findings corroborate prior observations by Wang et al [Wang and Eberly,Phys.Rev.Lett.105,083001 (2010)],demonstrating that NSDI occurs within a narrower time window in circular polarization compared to linear polarization.As a result,the yield of linear polarization was higher than that of circular polarization,aligning with the previously reported results.Notably,in the case of circular polarization,the time window further narrows with increasing intensity,attributed to a decrease in the time-of-flight.

Keywords: NSDI,knee structure,TDSE,shielding charge,helium,3D-TDSE

1.Introduction

Over the past three decades,we have witnessed remarkable progress in laser technology and the comprehension of nonlinear laser-matter interactions.This remarkable journey was recently honored by the prestigious Nobel Prize awarded to Gérard Mourou and Donna Strickland,acknowledging their significant contributions to the field [1].The utilization of ultrashort attosecond pulses has opened up exciting avenues for exploring fundamental aspects of the interaction between radiation and matter.These extremely short bursts of light enable researchers to delve into the intricate dynamics and processes that occur when radiation interacts with different materials.By harnessing attosecond pulses,scientists can investigate and unravel the underlying principles governing this interaction at an unprecedented temporal resolution,leading to new insights and discoveries in the field of lasermatter interactions [2–4].

High-intensity laser-atom interaction gives rise to highly nonlinear processes,including high-order harmonic generation(HHG)[5,6],above-threshold ionization(ATI)[7],nonsequential double ionization (NSDI) [8],etc.At non-perturbative intensities,the strength of the incident laser field becomes comparable to the Coulomb potential,causing a modification in the potential’s shape.As a result,electrons can tunnel through the potential barrier and rapidly accelerate in the laser field,detaching from the atomic nucleus within a fraction of a second.Subsequently,when the laser field changes direction,the electrons can re-encounter the parent ion.Depending on the nature of the interaction during the return,various phenomena occur;the recombination of the ionized electron upon its re-collision with the ion leads to HHG,scattering by the nucleus leads to ATI,and inelastic recollisions result in the detachment of additional electrons from the nucleus,known as NSDI.This explanation of the NSDI is called the re-scattering process [9–11].When the electron returns to the nucleus,it may not ionize the second electron,but instead excite it and cause it to be ejected to an excited bound state,from which it then escapes to the continuum.In this case,there is a time delay between the recollision of the first electron and the ionization of the second electron.This mechanism is called re-collision induced excitation with subsequent ionization (RESI) [12].Although an alternative theory is known as the shake-off theory[11,13,14].The shake-off theory attributes the detachment of the second electron from the nucleus to the matching of the electron wave function with abrupt changes that result from the separation of the first electron [15].

Double ionization has been observed in experimental studies[16–19]and modeled with the theory.Various models are employed to explain non-sequential double ionization,including the classical ensemble [20–25],S-matrix [26,27],quantitative re-scattering (QRS) model [28,29],and the solution of the time-dependent Schrödinger equation(TDSE).Out of these models,the numerical solution of TDSE is widely regarded as being more accurate [30–32].However,obtaining a three-dimensional numerical solution of the Schrödinger equation for atoms with more-than-one-electron,without any approximation,is practically impossible,due to the high volume of numerical calculations [11,33].For instance,in the case of the helium atom,the problem must be solved in six dimensions,three dimensions for the first electron and three dimensions for the second electron.NSDI has been investigated using the one-dimensional solution of TDSE [34–37] and a three-dimensional time-dependent Schrödinger equation (3D-TDSE) approach for the helium atom [38] with single active electron (SAE) approximation and time-dependent correlation potential for the inner electron.

While both linear and circular polarization can result in non-sequential double ionization,the specific interactions between the laser field and the electrons can differ due to the distinct characteristics of the electric field orientation.It is reported that NSDI yield decreases with the laser field ellipticity(∊)[23,39–43].In this study,we employ a full quantum mechanical method to solve the 3D-TDSE for the helium atom,utilizing the shielding charge approximation method.With this approximation,the interaction potential between electrons is eliminated,and the influence of the first electron on the second electron is accounted for by modifying the nuclear charge to an effective charge (eeff) in the TDSE.Consequently,the helium atom can be viewed as two hydrogen-like atoms with a nuclear charge ofeeff.While this approximation has been utilized for solving the Schrödinger equation for a long time [44],it has not been specifically applied to investigate NSDI at high laser intensities until now.

The primary objective of the three-dimensional solution is to compare the impact of linear and circular polarization on the NSDI of the helium atom.Our findings indicate a stronger influence of linear polarization compared to circular polarization for the helium atom.Initially,we acquired the knee structure,which displays complete accordance with the result that was reported by W Becker et al [45].Furthermore,the radius employed in our computations for the boundary after which double ionization occurs,concurs with the value stipulated in Refs.[46–48],a facet expounded upon in section 3.Subsequent to these calculations,we generated a plot illustrating the probability of ionization over time;notably,our graph exhibits a remarkable resemblance to the dataset presented by Wang et al [23].

2.Theoretical method

In this section,we will elaborate on our method,which involves solving 3D-TDSE for the helium atom in the presence of an external laser field.To simplify the calculations,we adopt the dipole approximation and work within the atomic unit system.Helium 3D-TDSE in the external laser field with dipole approximation in the atomic unit is given by:

E0is the driving laser field amplitude and f (t) is the pulse envelope.We specifically choose the pulse envelope function asf(t)=sin5(π+ωt/ 10) .The position of the electrons,denoted asr1(2)=(x1(2)i+y1(2)j+z1(2)k).‘a’ is the softcore potential constant to eliminate singularities at the origin(r1,(2)=0),which we set to a value ofa=0.01.In equation(1),we remove the interaction term,and instead,we model the interaction between the two electrons by modifying the nuclear charge (eeff).We chooseeeff=1.344eaccording to [44],because with this effective charge,the ground state energy of helium is obtained with an exact value of2.902a.u.,which agrees with the experimental value.Therefore,we have

Eq.(3)can be solved by employing the separation of the variables technique.Let us assume that the wave functionψ(r1,r2,t)can be expressed as the product of two individual wave functions:ψ(r1,t)andψ(r2,t).Consequently,Eq.(3)can be split into two separate equations,each resembling the behavior of a hydrogen-like atom.We can formulate the equations as follows:

Since we are not considering the spin factor,both electrons are indistinguishable.Therefore,we can solve equation (4) for just one of the electrons.We initialize the wave function asψ(r1,(2)=0,t=0) ∝ exp (-1.344r).In order to prevent reflections at the boundaries,we use a cosine mask function as cos1/8[(r-r0)/(r1(2)f-r0)]π/2[49],where|r0|=0.8|r1(2)f|,withr1(2)fbeing the endpoint of the spatial interval in the simulation frame.

To calculate the NSDI,we have to set the ionization boundary condition.Ris defined as the ionization boundary after which the electrons are assumed to be completely separated from the nucleus,and thus the atom is assumed to be ionized.That means if|r1| >|R|and|r2| <|R|or|r1| <|R|and|r2| >|R|single ionization occurs,and if|r1| >|R|and|r2| >|R|double ionization occurs [11].The following integration gives us the probability of ionization:

However,since the probability given above depends on time,and one may ask what time is more proper for the probability to be calculated.To calculate NSDI,we take a time average of the probability over the laser pulse duration,ast,wheretiandtfis initial and the ending time of the driving laser pulse,respectively,we setti=0.By plotting the time averaged probability of ionization as a function of intensity,the knee structure is obtained.

3.Results and discussion

Equation (4) was solved forλ=800nm,considering linear(C=1,D=0) and circular (C=D=1/2) polarization.The space intervals arex=[ -75,75] a.u.,y=[ -75,75 ]a.u.,andz=[ -50,50 ]a.u.and the time interval ist=[0,551] a.u..The time and space mesh are 1/ 160a.u.and 1/ 2a.u.respectively.Substituting the time-dependent wave function obtained from equation(4)into equation(5),and considering sixteen various values for intensity in the interval of 1× 1013to 1 ×1016W /cm2,the probability of ionization can be calculated.

Figure 1 represents the probability of ionization for two ionization boundaries of|R|=10 and20a.u..The black and red curves stand for linear and circular polarizations,respectively.As the figure shows,for|R|=10a.u.the probability of ionization shows a knee structure,according to experimental data of[9].Also,this boundary value,R,agrees with the calculations presented in Refs.[46–48].In these works,the authors found that for|Rc|=6a.u.the ground state energy becomes2.902a.u..Our next calculations confirm that higher values for ionization boundary do not affect the results (figure 1(b)).

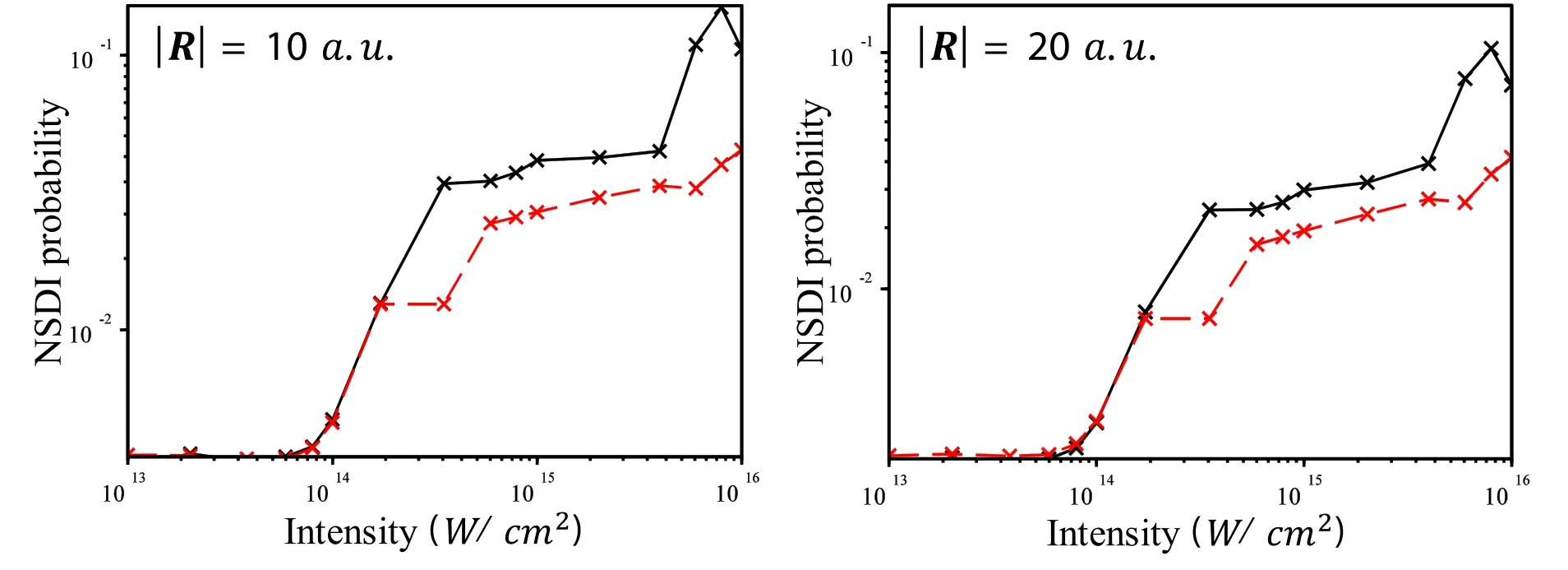
Figure 1.Comparing the knee structure of helium for| R|=10 and 20a .u .,the red dashed curve represents circular polarization,whereas the black curve represents linear polarization on the logarithmic scale.

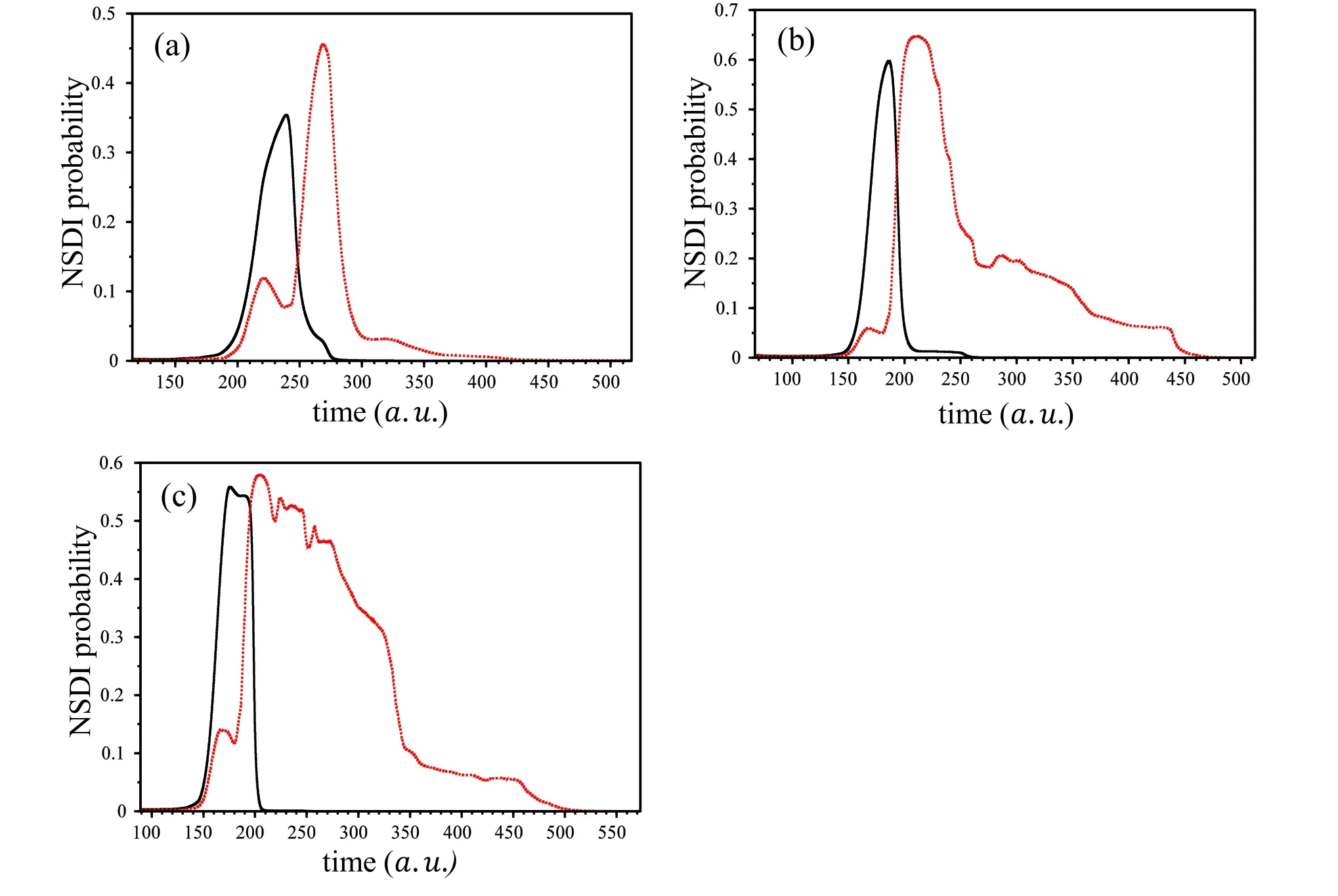
Figure 2.The nonsequential double ionization probability as a function of time for linear polarization (red dotted curve) and circular polarization (black curve) at| R|=10a .u .for the intensities: (a) 8 × 1014W /cm2,(b) 6 × 1015W /cm2,and (c) 8 × 1015W /cm2.

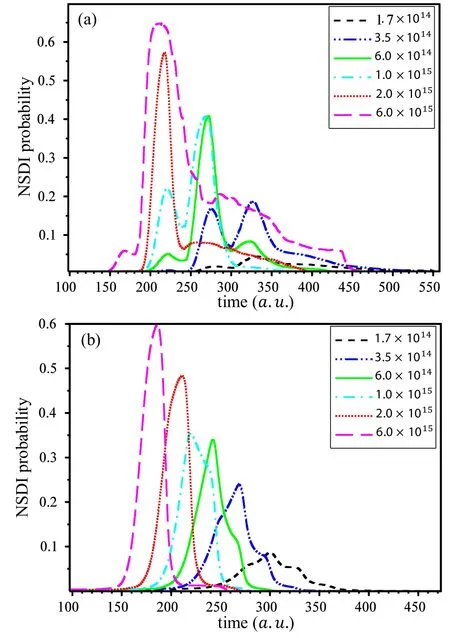
Figure 3.The nonsequential double ionization probability as a function of time at various intensities(W/ cm2)for(a)linear,and(b)circular polarization with| R|=10a .u .

As figure 1 shows,the yield of NSDI is higher for linear polarization compared to circular polarization.This result is also consistent with the theoretical findings reported in [50],which is achieved by the classical ensemble model.Figure 1 also shows a decrease in the intensity around the intensity of 1 ×1016W /cm2.This is because we are close to relativistic intensities and our model does not work properly in this regime.These results reassured us that our model has sufficient firmness.Also,they have enough agreement with the experimental results [40].

In the following,we investigated the probability of ionization over time for some intensities at|R|=10a.u..To do so,we plot the probability of ionization as a function of time for a fixed intensity.As depicted in figure 2,the NSDI probability for linear polarization is extended more in time compared to circular polarization,that is,double the ionization probability for circular polarization drops quickly in time.One can conclude that for circular polarization electrons return back to their parent ion sooner compared to linearly polarized electric field.This can be interpreted more technically as follows:circularly polarized electric field prevents spreading the electron wave function in the space,more so than linearly polarized field.In an unpublished work[51],we show that the circularly polarized electric field rotates the electron wave functions around the parent ion and confine it more around the nucleus.But,the linearly polarized field moves the electrons’ wave function forth and back,and causes it to spread in the space.Therefore,one can expect that for linear polarization,the electrons’ wave function is observed more in time in the farther areas,and this issue can increase the time of the electron presence in the distant regions and thus the ionization time.

Our result is in good agreement with the experimental results presented by Wang and Eberly[23].They show that the ionization time decreases with ellipticity.They employed the term‘narrower time window,’and this window becomes even narrower as the ellipticity parameter increases,consistent with our obtained results.Of course,they have investigated the problem for a specific intensity for different ellipticity parameter,but we obtained the narrow time window for different intensities for two ellipticity parameter (∊=0 and 1).

In figure 3,we present a comparison of NSDI probability for linear (figure 3(a)) and circular (figure 3(b)) polarization as a function of time for different intensities.For two cases,as the intensity increases,the ionization ‘peak’ shifts towards shorter times.This result can be explained rather straightforwardly.As the intensity rises,the threshold intensity required for double ionization to occur is reached earlier within the optical cycle.It is no longer necessary to wait for a full optical cycle with maximum intensity for ionization to take place.The earlier occurrence of the necessary intensity threshold leads to the observed shift in the ionization peak towards shorter times.

Another observation from figure 3 is that the ionization time decreases with increasing intensity for circular polarization.This can be explained by considering the time-offlight definition,ToF=wheredrepresents the distance from the nucleus,mandqare the electrons'mass and charge,respectively,Upis electrons' kinetic energy,in this case,the pondermotive energy is defined aswhereE0is the electric field amplitude of the driving laser field andωis the frequency.When the amplitude of the incident laser electric field is increased,the ponderomotive energy also increases.As a result,the electron’s time of flight decreases.Therefore,with the higher intensity of the incident field double ionization occurs within a shorter period of time,as depicted in figure 3(b) for circular polarization.

In the case of linear polarization,the time period of NSDI exhibits fluctuations,meaning it can show ascending or descending behavior,as shown in Fig.3(a).These fluctuations are likely due to the larger distance the electron travels from the nucleus in linear polarization compared to circular polarization.Thus,the parameterdalso plays a significant role,and the growth rate ofdandUpis comparable.This factor causes the time interval of NSDI in linear polarization to vary for different intensities.

4.Conclusion

In this study,we conducted an investigation of non-sequential double ionization (NSDI) for the helium atom under both linear and circular polarization.Despite employing an approximation called shielding charge approximation,we successfully observed the knee structure,which is indicative of the double ionization phenomenon.Our findings revealed the superiority of linear polarization in NSDI,which aligns with the experimental results.

Based on the obtained results,the superiority of linear polarization over circular polarization can be attributed to the time interval of NSDI.In linear polarization,the interaction time is longer compared to circular polarization.This longer interaction time is directly related to the electron’s collision with the parent ion.In linear polarization,the electron re-collides with the nucleus once per half of the optical cycle,whereas,in circular polarization,it only undergoes one re-collision with the nucleus at the end of the incident pulse.Therefore,this discrepancy in re-collision events leads to a longer interaction time in linear polarization compared to circular polarization.

Acknowledgments

M Sabaeian and M Zakavi would like to thank Shahid Chamran University of Ahvaz for supporting this research under the grant number SCU.SP1401.259.

Disclosures

The authors declare no conflicts of interest.

ORCID iDs