Enhanced quantum resources via two distant atom-cavity systems under the influence of atomic dissipation

M Setodeh Kheirabady,M K Tavassoly,M Rafeie and E Ghasemian

1 Laser and Optics Group,Faculty of Physics,Yazd University,Yazd 89195-741,Iran

2 Department of Electrical Engineering,Faculty of Intelligent Systems Engineering and Data Science,Persian Gulf University,Bushehr,Iran

Abstract Quantum resources such as entanglement and coherence are the holy grail for modern quantum technologies.Although the unwanted environmental effects tackle quantum information processing tasks,suprisingly these key quantum resources may be protected and even enhanced by the implementation of some special hybrid open quantum systems.Here,we aim to show how a dissipative atom-cavity-system can be accomplished to generate enhanced quantum resources.To do so,we consider a couple of dissipative cavities,where each one contains two effective two-level atoms interacting with a single-mode cavity field.In practical applications,a classical laser field may be applied to drive each atomic subsystem.After driving the system,a Bell-state measurement is performed on the output of the system to quantify the entanglement and coherence.The obtained results reveal that the remote entanglement and coherence between the atoms existing inside the two distant cavities are not only enhanced,but can be stabilized,even under the action of dissipation.In contrast,the local entanglement between two atoms inside each dissipative cavity attenuates due to the presence of unwanted environmental effects.Nevertheless,the local coherence may show the same behavior as the remote coherence.Besides,the system provides the steady state entanglement in various interaction regimes,particularly in the strong atom-cavity coupling and with relatively large detuning.More interestingly,our numerical analyses demonstrate that the system may show a memory effect due to the fact that the death and revival of the entanglement take place during the interaction.Our proposed model may find potential applications for the implementation of long distance quantum networks.In particular,it facilitates the distribution of quantum resources between the nodes of large-scale quantum networks for secure communication.

Keywords: remote entanglement and coherence,atomic dissipation,steady state entanglement,Bell-state measurement

1.Introduction

Construction and manipulation of large-scale quantum networks facilitate secure communication,provide enhanced quantum information processing and allow fundamental tests of quantum mechanics through the distribution of quantum resources shared between the networks' components [1–6].Entanglement is a key quantum resource for the implementation of quantum networks and guarantees inseparable quantum correlations between distant parties of composite quantum systems.Particularly,the remote entanglement between stationary qubits is an essential ingredient for the establishment of quantum networks.This type of entanglement may be generated by transferring photons between different nodes of a network[7].On the other hand,when two particles,i.e.trapped atomic ions,experience a shared potential,the local entanglement may be expected via motional degrees of freedom [8].Notably,both local entanglement[9,10],and remote entanglement[11,12]have been experimentally realized,via single-photon protocols.

Although it is possible to experimentally generate entanglement between quantum systems,the protection of this key quantity against unwanted environmental effects is still the hardest challenge toward reliable quantum technologies.So it would be of fundamental interest to seek new approaches to engineer strongly correlated states with the help and exploitation of the inevitable environmental effects,i.e.dissipation process [13–16].Several quantum information platforms are implemented based on reliable ways of distributing quantum resources in large computing architectures or over long distances for quantum communication [17].The coupling of a system with its environment may be manipulated for the establishment of entanglement.In fact,entanglement is induced by the action of a global environment on the composite quantum systems [18].Interestingly,dissipation allows a promising venue for the stabilization of entanglement [19,20].This realization may be accomplished for the generation of stationary entanglement between noninteracting (independent) two-qubit systems [21,22].

Also,it is experimentally demonstrated that entanglement can be generated between two given quantum systems via applying appropriate measurements on them.In practice,the entangled states have been realized by stimulating two separate systems simultaneously and monitoring their emissions.More interestingly,the mutual state can be characterized without learning the source of any given photon.This approach presents some profound advantages,e.g.it facilitates a scalable technology,since the system components can be far apart.The measurement-based entanglement has been reported by measuring optical emissions from two remote qubits [23].It is noteworthy that,the measurement-based quantum computation can be established by performing successive measurements on highly entangled qubits [24].

Quantum coherence is another key quantum resource that makes clear the boundary between the quantum and classical contexts.Some extensive quantum phenomena such as interference [25],laser [26],superconductivity [27] and superfluidity [28,29] may be interpreted based on quantum coherence.In fact,quantum coherence provides some profound merits for quantum metrology [30,31],quantum key distribution [32],entanglement creation [33,34].In this regard,the remote creation of coherence in a quantum system has been reported in [35].Also,the stability of quantum coherence in composite systems under the action of local dissipation has been studied as a resource for remote state preparation [36].

Summing up,both entanglement and coherence play a crucial role in quantum information processing.The interconversion between them has been discussed and shown that l1-norm of coherence and coherence concurrence coincide with each other [37].Further investigation of these two key quantum resources,and finding the relationship between them may open a new venue for understanding the real quantum world [38].Based on the above facts,we motivated to study the generation of remote quantum entanglement and coherence based on the Bell-state measurement(BSM)mechanism under the action of atomic dissipation in a new schematic realizable model.In fact,we propose an experimentally accessible composite system consisting of two distant identical cavities,where each one contains two dissipative threelevel Ξ-type atoms interacting with a single-mode quantized field and a classical driving field.We follow the dynamical evolution of the system and evaluate the quantum resources corresponding to the atomic subsystems,e.g.remote and local entanglement and coherence.We show that although the local quantum resources are plagued due to the presence of unwanted environmental dissipation,both remote entanglement and coherence may be enhanced and stabilized by increasing the atomic damping rate.This is an outstanding feature of our proposed model which facilitates the establishment of a quantum network for long-distance quantum communication.Besides,our numerical analyses demonstrate that the dynamics of remote entanglement and coherence strongly depend on the initial state of the system as well as the other involved parameters,i.e.the detuning parameter and atom-cavity coupling strength.In particular,the enhanced remote steady state entanglement may be realized by considering a relatively large detuning parameter in the weak atom-cavity interaction regime.Interestingly,both the steady state remote entanglement and coherence possess the same dynamical patterns under the similar physical conditions,while the initial amounts of these quantities can be readily controlled by tuning the initial state of the system.

The contents of this paper are organized as follows.The system and its model Hamiltonian are introduced in section 2.Our numerical analyses including the study of remote and local quantum resources,e.g.entanglement and coherence are presented in section 3.Finally,the summary and concluding remarks can be found in section 4.

2.The model and its solution

Let us introduce our proposed theoretical scheme for the generation of remote entanglement based on BSM technique.The system under consideration constitutes two independent identical cavities where two dissipative three-level Ξ-type atoms located in each cavity interact with a single-mode quantized field under the action of a classical driving field.The three levels of atoms from top to bottom are labeled as∣r〉,∣e〉,and ∣g〉,respectively.The transition frequency between levels |r〉 and |e〉 is highly detuned from the other transition frequencies,so that one can neglect the high level (the same method has been performed in[39]).By such an assumption,the three-level atoms are viewed by the effective two-level atoms.

The numbered atoms with 1,2(3,4)are located in cavity A (B) (see figure 1).The Hamiltonian for each pair of atoms that are driven by a classical field and interact with a single-mode quantized cavity field is given by (ħ=1),

where ω and ωdare cavity and driven field frequencies,ω0is the atomic transition frequency between levels ∣g〉 and ∣e〉,gidenotes the coupling strength between ith atom and its cavity mode,Ωiis the Rabi frequency of classical field,and ˆa(ˆ†a)is the bosonic annihilation(creation)operator of the cavity field.In equation (1) the atomic operators are defined as,

From now on we assume that Δ=ωd−ω0=0,giand Ωiare real quantities,gi=gand Ωi=Ω for all atoms.Accordingly,the Hamiltonian in the interaction picture,regarding the mentioned conditions reads as,

where δ=ω0−ω.Under the following unitary transformation [39]

In the case of large detuning δ ≫g,we can neglect all terms that rotate quickly and as a result the interaction picture Hamiltonian (5) readily converts to an effective Hamiltonian with the following form [40],

in whichλ=is the effective atom-field coupling.A remarkable result of this manipulation is that,the final effective Hamiltonian does not depend on the number of photons in the cavity.

Now,we want to consider the influence of dissipation on the system.Since the latest effective Hamiltonian presented in equation(7)is independent of the cavity modes,the presence of photons does not affect the dynamics of the system and one can neglect the field decay.However,the atomic spontaneous emission which is resulted from the interaction between the atomic system and its vacuum environment cannot be ignored.Therefore,the dissipative solution of each subsystem can be obtained by the following Lindblad master equation [41],

where γ stands for the atomic damping rate anddenotes the Lindblad operator with the following form,

To deal with the dynamics of the system,let us introduce the initial state of atoms as follows,

with the assumption that a and b are real numbers.By different choices of the coefficients a and b,the initial diatomic states in each cavity can be(maximally or partially)entangled or separable.In this study we have chosen the same initial states for two cavity subsystems.i.e.a=b.We numerically find the solution of master equation in(8) using the quantum toolbox in Python(QuTiP package)[42].Therefore,the timedependent solution of the whole system is given by direct multiplication of the quantum states of the two subsystems,

Equation(12)implies that the atoms labeled with 1 and 4 live in two distant cavities,and there is no initial entanglement between them.Hence,to generate entanglement between these target atoms,we may resort to the BSM which is a suitable way to deal with distant atom-cavity systems.The atomic BSM has been frequently used for creating entanglement,entanglement swapping and quantum teleportation tasks[43–45].It should be noted that,the influence of cavity modes has been removed by a unitary transformation and via considering some other assumptions,so we have only contributions from atoms 1-4,and therefore,we have to perform atomic BSM.Further details about BSM and its applications can be found in the relevant literature [46,47].

To achieve this purpose,we choose the following atomic Bell state,

by which we arrive at the necessary projection operatorby which our BSM task can then be performed.

Finally,one arrives at the following quantum state by the action of latter projection operator on the total state |ψ(t)〉totpresented in (12),

3.Numerical analyses of quantum resources

Now we are ready to numerically study the desired key quantum resources,e.g.entanglement and coherence between the atomic subsystems.At first,we introduce the concurrence and l1-norm of coherence to quantify the amount of entanglement and coherence between distant atomic subsystem(remote quantum resources),respectively,and then analyze the local counterparts,namely the entanglement and coherence corresponding to the atoms placed in each cavity.

3.1.Entanglement

To determine the amount of entanglement between the two atoms 1 and 4,we enumerate concurrence which is a wellknown measure of the entanglement between two two-level atoms.This quantity was initially introduced by Wootters[48] and defined as follows,

3.2.Quantum coherence

Quantum coherence is another key quantity that is of fundamental interest for doing quantum information processing tasks[49].This key quantity has been used to distinguish the quantum world from the classical realm.Among various quantities for quantifying quantum coherence,let us introduce the l1-norm of coherence [50],

3.3.Numerical analyses: dynamics and steady state remote quantum features

In what follows,we numerically analyze the evolution of entanglement and coherence between the components of the system during the interaction as well as at the steady state regime.Particularly,we evaluate the concurrence and l1-norm of coherence associated with atomic quantum states by considering different system parameters and interaction regimes.

3.3.1.Entanglement dynamics with BSM.Let us start with the time evolution of concurrence.Figure 2 shows the effect of the detuning parameter and atomic loss on the time evolution of entanglement between the first and fourth atoms against the scaled time kt.Indeed,these patterns correspond to the remote atom-atom entanglement between two distant atoms 1 and 4.Since we are intersted in the generation of entangled state,let us consider the case in which there is no initial entanglement between the atoms.Assume a separable state for the atomic subsystems which identified with a=0.As the system is driven by the external fields,the atoms become entangled.Interestingly,the system experiences death and revival of entanglement during the interaction.The latter phenomenon may recall the memory effect which indicates that there is a temporal flow of information from the environment to the system.Finally,the entanglement is stabilized as time goes on.More importantly,in both figures 2(a) and (b),the amount of steady state entanglement increases by increasing the atomic dissipation rate.Moreover,a rough comparison between these plots reveals that although the system provides a relatively large amount of entanglement after the onset of interaction in the small detuning regime,i.e.δ/k=1 shown in plot 2(a),the steady state entanglement may be enhanced by considering a larger detuning parameter,i.e.δ/k=2 according to figure 2(b).In conclusion,the atomic dissipation process may be exploited to obtain enhanced steady state entanglement,especially,in the large detuning regime.

Now let us follow the patterns of entanglement by considering another initial state for the atomic subsystems.Hence,we replace the parameter a=0 with a=0.5 and plot the concurrence against the scaled time kt as depicted in figure 3.In contrast to figure 2,in this case,the atoms are entangled at the onset of interaction.However,they experience a relatively fast decay of entanglement during the interaction.In analogy with the results in figure 2,the system may recover a considerable amount of its initial entanglement in the steady state regime if it is initiated with a relatively large detuning parameter.Note that the atoms are almost always entangled in this case.In fact,the system does not experience the death of entanglement except with γ/k=0.1 near the steady state regime.Therefore,the entanglement dynamics strongly depends on the initial state of the system and its characteristics.Indeed,the atomic entangled states can be generated,and manipulated by choosing the desired initial states of the atoms and via adjusting the interaction regimes and the involved parameters in the model.

3.3.2.Entanglement with BSM in the steady state.Now,we proceed to evaluate the steady state entanglement generated via BSM.Figures 4(a),(b) ascertains that the steady state entanglement can be improved by increasing the atomic dissipation rate,especially in the weak (strong) atom-cavity coupling regime with small (large) detuning parameter.In fact,the system generates stationary entanglement in both weak and strong atom-cavity regimes when initiated with small and large detuning parameters,respectively.Also,the steady state entanglement is preserved in a larger atom-cavity coupling range for the relatively large detuning parameters.Generally,figure 4 demonstrates that although the steady state entanglement dies out with a small atomic damping rate in both small and large detuning regimes,it more survives against the unwanted effects by increasing the atomic dissipation parameter.For instance in plot 4(c),the system does not experience the death of steady state entanglement with larger detuning parameters and enhanced atomic dissipation rate.

Let us further investigate the effects of the system parameters on the steady state entanglement.Figure 5 demonstrates that the entanglement gradually increases and approaches its maximum value by increasing the detuning parameter.Note that for a given detuning parameter,the maximum value of steady state entanglement can be enhanced by decreasing the atom-cavity coupling strength.Besides,the entanglement between the atoms is strengthened if the system undergoes the stronger atomic dissipation process.For instance,for δ/k=6 and g/k=0.25,the concurrence between the distant atoms reads as C ≃0.8 and C ≃0.95 for γ/k=0.1 and γ/k=1.0,respectively.Briefly,one can conclude that the death of entanglement is just plausible with the small detuning,low damping rate,and relatively strong atom-cavity regime;otherwise,the system can provide a considerable stationary remote entanglement,especially,in the large detuning regime.

3.4.Quantum coherence after BSM

Now we intend to study the generated quantum coherence between distant atoms via our proposed approach,e.g.remote quantum coherence based on BSM.In analogy with entanglement,at first,we investigate the time evolution of quantum coherence between the distant atoms and then evaluate its steady state behavior.

3.4.1.Dynamical quantum coherence after BSM.The effect of atom-cavity coupling strength on the time evolution of quantum coherence between two distant atoms after BSM is plotted in figure 6.These two plots are corresponding to different initial states of the system respectively identified with a=0.5 and a=0.As may be seen the patterns of quantum coherence strongly depend on the initial state of the system,particularly,in the early time.Also,the maximum value of quantum coherence takes place at the beginning of the interaction as shown in figure 6(a),while there is no initial quantum coherence between the two atoms for the second case illustrated in figure 6(b).In contrast,the quantum coherence follows the same behavior at the steady state in both cases such that it tends to constant value which can be tuning the atom-cavity interaction strength.Generally,the results confirm that the mentioned coupling strength has no considerable effect on the quantum coherence at the onset and even during the interaction.In contrast,the enhancement of quantum coherence may be realized through decreasing the atom-cavity coupling constant as the system approaches its steady state.

Here,we proceed to further investigate the dynamical evolution of quantum coherence under the influence of system parameters.The results in figure 7 show that increasing of the atomic dissipation rate not only improves the quantum coherence between distant atoms but also results in the stability of this key quantum resource.Once again,the patterns and initial values of quantum coherence vary with respect to the chosen initial states of the system.However,as the system approaches the steady state regime,the enhanced quantum coherence becomes more clear by increasing the atomic dissipation.It is worth noting that the system can be exploited to provide stabilized quantum coherence in longrange interaction regimes and diverse physical conditions.

3.4.2.Steady state quantum coherence after BSM.The enhanced quantum coherence between the two distant atoms at the steady state is plotted in figure 8.One observes that the remote quantum coherence gradually enhances by increasing the detuning parameter,especially,in the relatively strong atom-cavity interaction regime and with low damping rate as shown in figure 8(a).In contrast,the generated quantum coherence fastly improves in the weak interaction regime,i.e.g/k=0.25 with a relatively large damping rate,e.g.γ/k=1.0 as depicted in figure 8(b).Note that there is no considerable amount of quantum coherence in the steady state if the system is initialized with a small detuning parameter,low atomic damping rate,and relatively strong atom-field strength as can be found in figure 8(a).Besides,figure 8 demonstrates that the steady state quantum coherence generally enhances by increasing the atomic damping rate.It is worth noting that both generated entanglement and quantum coherence,respectively presented in figures 5 and 8,follow the same patterns.

3.5.Local entanglement based on BSM

Besides the generation of remote quantum resources via the whole considered system investigated above,entanglement may be generated between the components of each subsystem.We study the dynamical evolution of local atom-atom entanglement corresponding to the same subsystems for different detuning parameters in the absence of the dissipation process in figure 9.Generally,the local entanglement follows ideal oscillatory behavior such that this quantity undergoes very fast oscillations in the small detuning regime illustrated in figure 9(a).In fact,the frequency of oscillation is inversely proportional to the detuning parameter.Physically,the atoms periodically become maximally entangled (C=1) and disentangled(C=0)during the interaction in the absence of the dissipation.

Now,let us consider the effect of dissipation process,and re-analyze the local atom-atom entanglement for different initial states of the system.The results presented in figure 10 show that the concurrence undergoes decaying oscillatory patterns such that the local entanglement between atoms plagues in the presence of atomic dissipation.For both cases with initial states characterized with a=1 and a=0,respectively,there is no initial entanglement between the two atoms,however,they become entangled after the onset of interaction.In contrast to the generated remote atom-atom entanglement depicted in figures 2 and 3,in this case one can see that the atoms in each cavity faster become disentangled by increasing the atomic damping rate.Indeed,our results show that the unwanted environmental effects,e.g.the atomic dissipation can be exploited to generate the enhanced remote atom-atom entanglement,even at the steady state regime,while the individual quantum cavity containing a couple of two-level atoms cannot provide steady state entanglement.Therefore,such a composite system may be useful for the implementation of long-distance quantum networks.

3.6.Local quantum coherence based on BSM

To give a dipper insight into this system,let us examine the dynamical evolution of the local coherence between two atoms in each cavity via BSM.Figure 11 is plotted with the same parameters chosen in figure 6 which shows the evolution of remote coherence between two atoms in distant cavities.Generally speaking in both cases,it is observed that for a=0.5 (a=0) the system is initiated with maximum(minimum) quantum coherence,however,the local coherence between the atoms decreases (increases) in early times after the beginning of the interaction.Interestingly,the steady state coherence between the atoms is almost equal in both plots of figure 11.In other words,although the coherence between the atoms strongly depends on the initial state of the system during the interaction,the amounts of steady state coherence are almost equal for these chosen initial states.Besides,the results show that the local steady state coherence may be enhanced by increasing the atomcavity coupling strength.In contrast,our above analyses show that the enhanced remote coherence at steady state regime can be expected in the relatively weak atom-cavity interaction.Consequently,the considered system can provide both remote and local dependence on the chosen atomcavity interaction regimes.

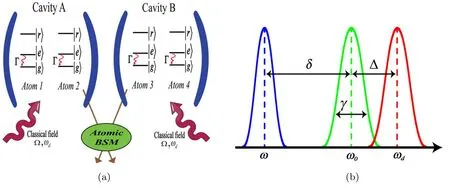
Figure 1.(a)Schematic representation of the considered model.Two remote single-mode optical cavities;each one comprises two three-level atoms that are driven by a classical field and also interact with the quantized field.(b)Detunings and frequencies of the system:the effective two-level atoms with transition frequency ω0 and linewidth Γ are driven by a classical field at frequency ωd.

Figure 2.The entanglement dynamics as a function of the scaled time kt.We have chosen a=0,g/k=0.5,and δ/k=1 in(a),δ/k=2 in(b).Note that we have set k=1 MHz to scale the system parameters in our numerical analyses.

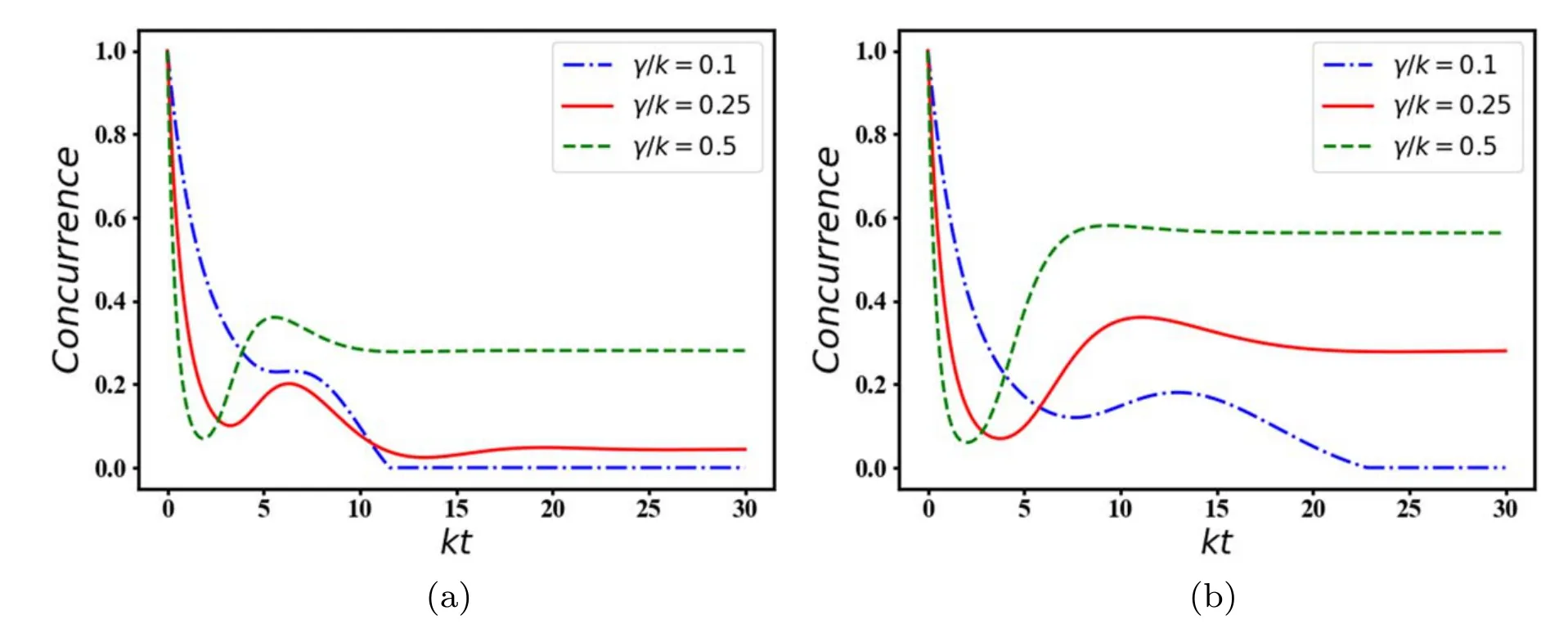
Figure 3.The entanglement dynamics as a function of the scaled time kt.We have chosen a=0.5,g/k=0.5,and δ/k=1 in (a),δ/k=2 in (b).

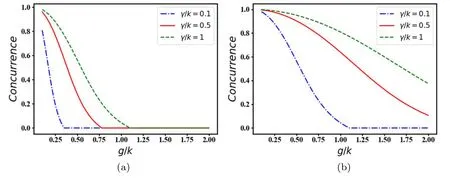
Figure 4.The steady state concurrence as a function of g/k.We have chosen δ=1 in (a),δ=10 in (b).

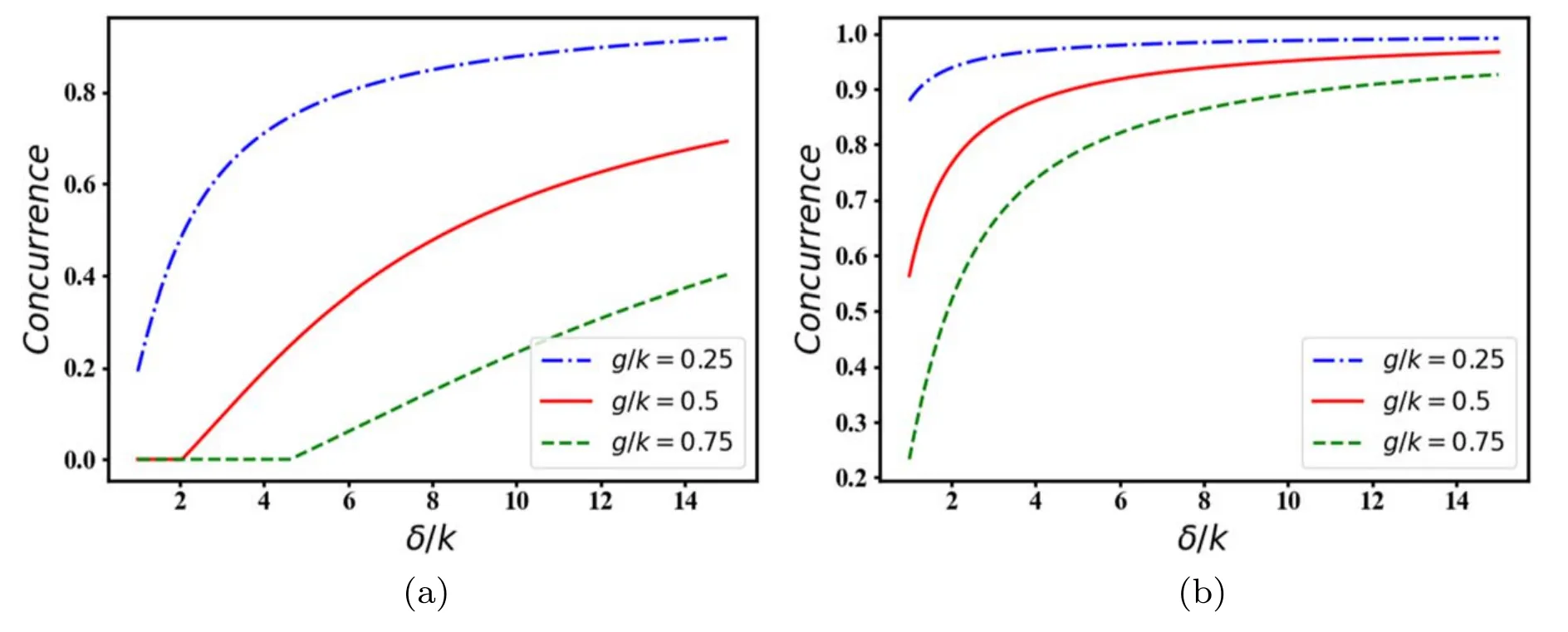
Figure 5.The steady state concurrence as a function of δ/k.We have chosen γ/k=0.1 in (a),γ/k=1.0 in (b).

Figure 6.The time evolution of quantum coherence as a function of the scaled time kt for γ/k=0.5.We have chosen a=0.5 in(a),a=0 in (b).

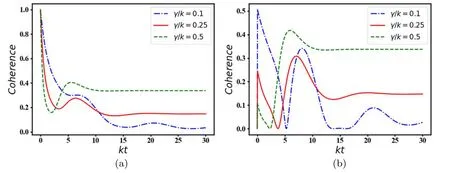
Figure 7.The time evolution of quantum coherence as a function of the scaled time kt for g/k=0.5.We have chosen a=0.5 in (a),a=0 in (b).

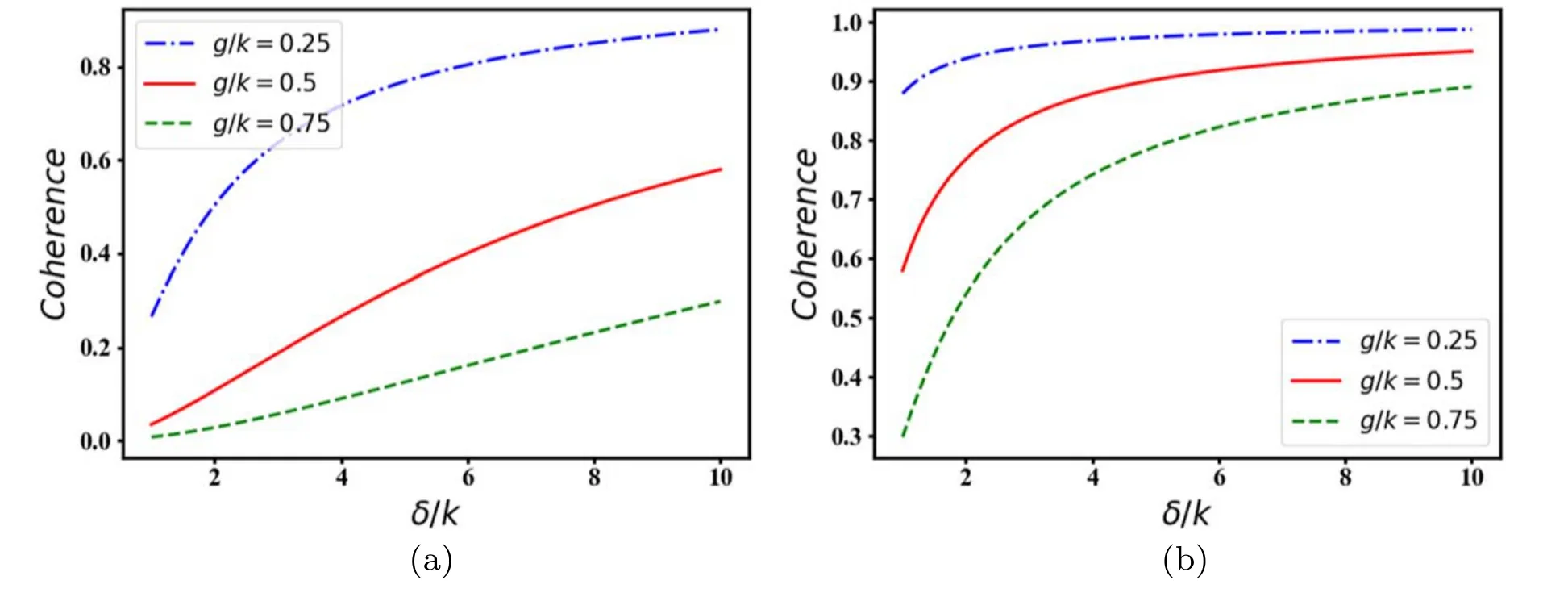
Figure 8.The steady state coherence as a function of δ/k for γ/k=0.5.We have chosen γ/k=0.1 in (a),and γ/k=1.0 in (b).

Figure 9.Atom-atom entanglement dynamics as a function of the scaled time kt.We have chosen γ/k=0,g/k=1,and a=1.

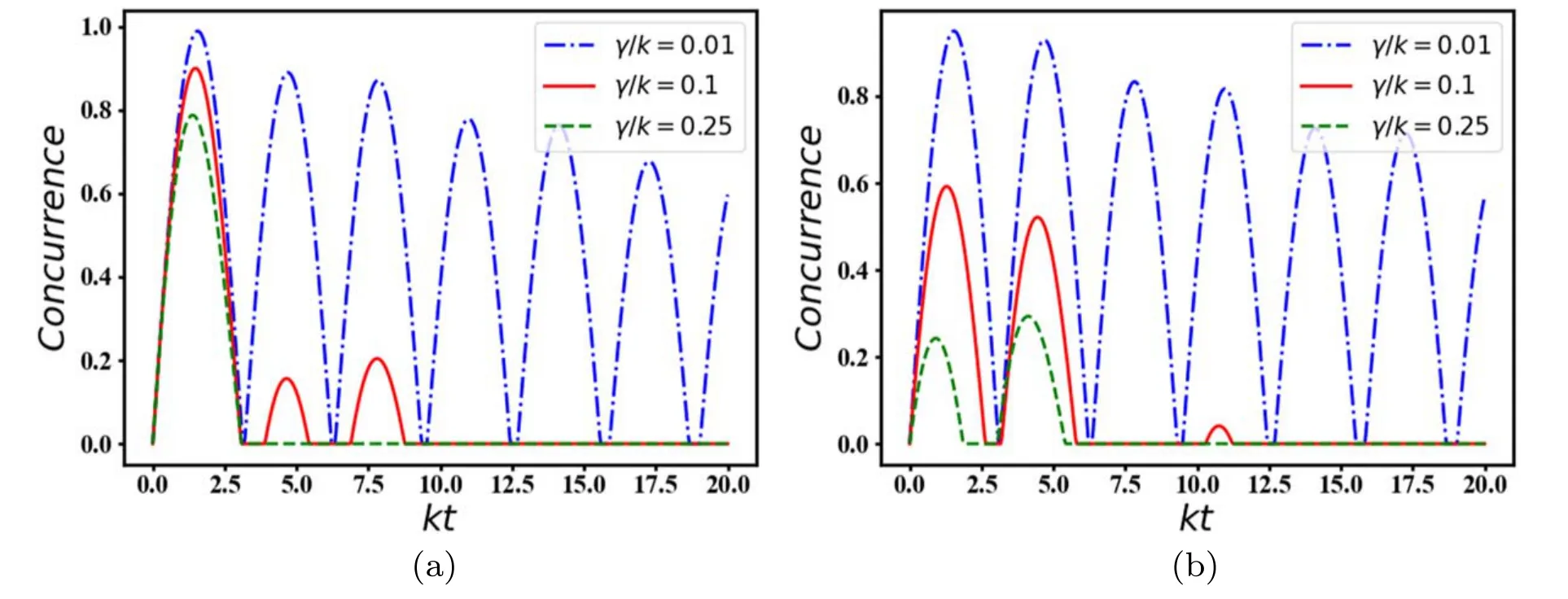
Figure 10.Atom-atom entanglement dynamics as a function of the scaled time kt.We have chosen δ/k=2,g/k=1,and a=1 in(a),a=0 in (b).

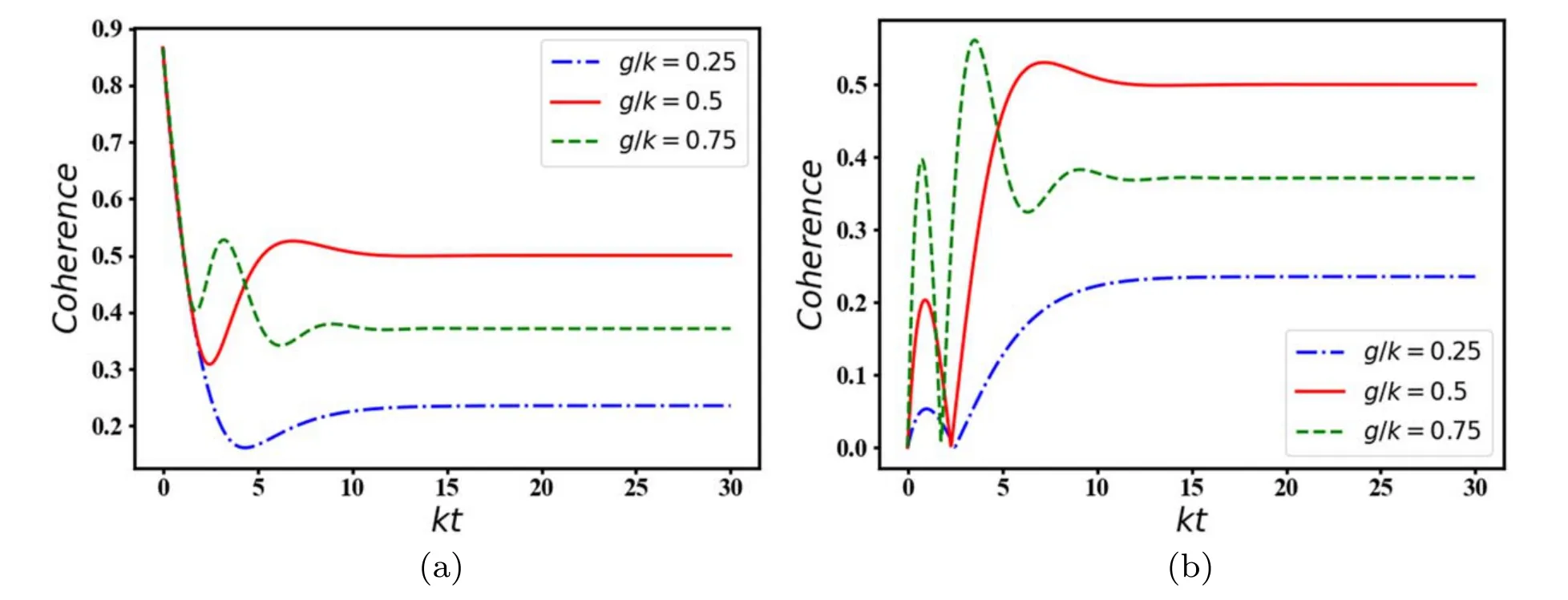
Figure 11.The time evolution of quantum coherence for one subsystem as a function of the scaled time kt for γ/k=0.5.We have chosen a=0.5 in (a),a=0 in (b).

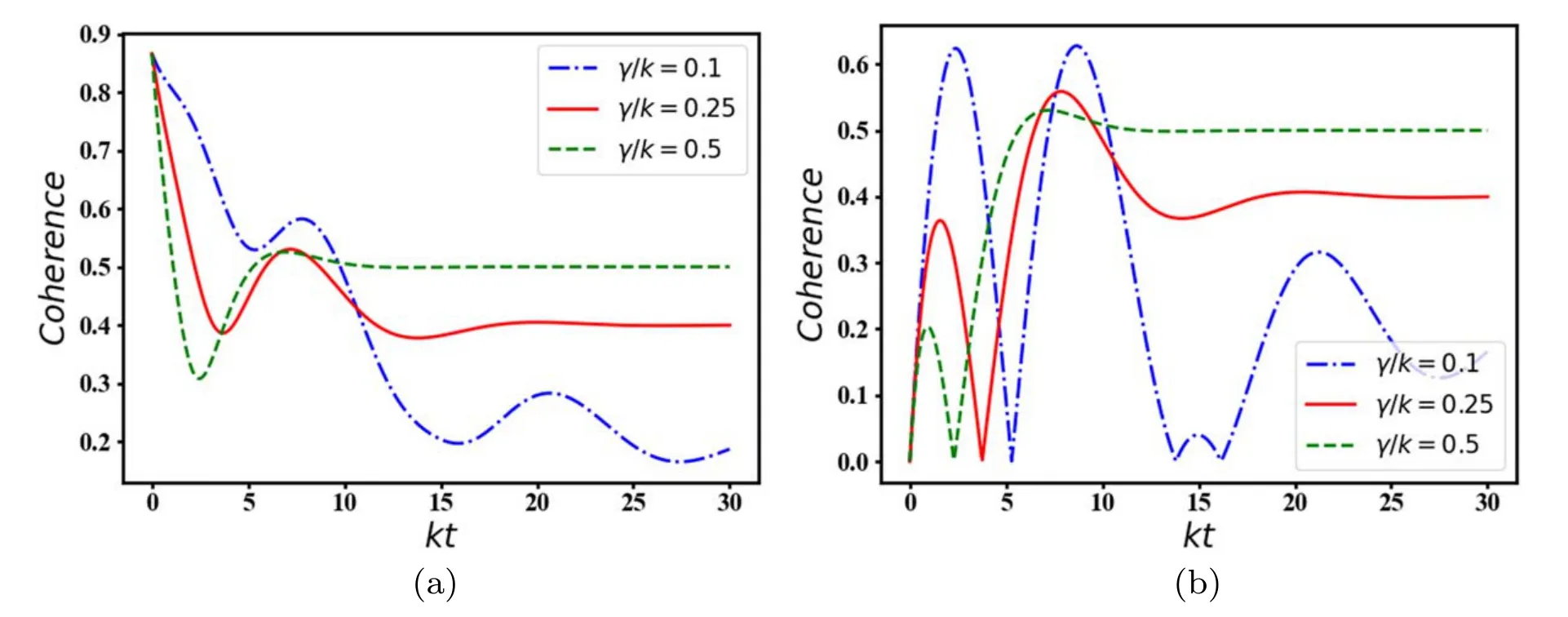
Figure 12.The time evolution of quantum coherence for one subsystem as a function of the scaled time kt for g/k=0.5.We have chosen a=0.5 in (a),a=0 in (b).

To complete our discussion,let us investigate the effect of atomic damping on the time evolution of local coherence between the atoms as presented in figure 12.A rough comparison with the results presented in figure 7 reveals that both local and remote coherence follow the same dynamical evolution.In particular,the coherence shows irregular decaying (improving) oscillatory patterns for a=0.5 (a=0)in early times,and then steady state coherence may be stabilized by increasing the atomic damping rate.

In conclusion,our results demonstrate that the system may be manipulated to provide enhanced and stabilized quantum resources even at steady state.Briefly,the main practical obstacle in quantum sciences,e.g.the presence of unwanted environmental effects,may be harnessed for doing useful tasks such as quantum communication and quantum teleportation.In fact,we show that,it is possible to bypass and overcome the challenges corresponding to dissipation by designing and accomplishing remote atom-cavity systems under experimental feasible conditions as well as applying the proper transformation.Hence,our proposed model is a promising platform for quantum science and technology due to the fact that,it facilitate the preparation of remote entangled states under realistic conditions.

4.Summary and concluding remarks

Although inevitably environmental effects in a realistic experimental setting seem to be the strongest adversaries in quantum information science,it is possible to exploit them for generation of the enhanced quantum resources.In this regard,we considered a composite open quantum system consisting of a couple of cavities each containing two effective two-level atoms interacting with a single-mode cavity field under the action of a classical driving laser field.At first,we introduced the system and derived the respective Hamiltonian.As a remarkable result,we have shown that the system may be manipulated such that the final effective Hamiltonian does not depend on the field intensity,i.e.the number of photons in the cavity,and therefore,the field decay may be neglected.Our numerical analyses include the investigation of both remote and local quatum resouces at various physical situations.In particular,we showed that the system provides the enhanced remote atom-atom entanglement between two distant atoms.Also,the death and birth of remote entanglement may occur,which is a signature of the memory effect.More importantly,the amount of steady state entanglement may be improved by increasing the atomic dissipation rate.Also,our findings reveal that the atomic dissipation may affect the quantum resources in different ways.For example,it enhances the remote atom-atom entanglement even at the steady state regime,while the local entanglement cannot be protected against the atomic dissipation in the steady state regime.

Moreover,the stabilized quantum coherence can be expected by the implementation of our considered system in the long-range interaction regimes and at various physical conditions,i.e.manipulating the atom-cavity interaction regime,detuning parameter,atomic damping rate,as well as the preparing initial state of the system.It is worth noting that in contrast to the local entanglement which plagues in the presence of atomic dissipation,the local coherence at steady state regime is enhanced and stabilized by providing the appropriate conditions.Breifly,reliable quantum sources may be generated and even improved by exploiting such an open atom-cavity system and harnessing the atomic dissipation.

The power of future quantum networks may be extracted through the entanglement shared between the network nodes.Also,the reliable and useful quantum networks may be established if quantum resources,e.g.entangled states,can be distributed with high confidence over long periods.Hence,we strongly hope that our proposed model may find its potential applications for the investigation and also the preservation of remote entangled states.Particularly,such a system may be viewed as a key building block for extended quantum networks.

ORCID iDs