基于多目标粒子群的电动汽车优化充电策略

李婷婷,娄 柯,王 园,徐华超

(1.安徽工程大学 机械工程学院,安徽 芜湖 241000;2.安徽工程大学 电气工程学院,安徽 芜湖 241000)

在能源和环境保护的双重压力下,电动汽车(Electric Vehicles,EV)在世界各地迅速发展。由于电动汽车具有间歇性、随机性和不确定性,其以高渗透率随机接入电网充电,影响电力系统的安全与稳定[1-2]。因此,有必要制定有效的充电控制策略以引导电动汽车有序充电。EV充电负荷数据的准确预测对充电控制策略的研究较为重要。文献[3～4]分析了EV日行驶里程、起始充电时刻等影响建模的因素,采用蒙特卡洛法对充电负荷进行预测。同时EV可作为储能装置,车辆到电网(Vehicle to Grid,V2G)旨在将电动汽车整合到电网中。在V2G场景下,电动汽车被视为分布式发电/存储系统和动态灵活负载,可用于平衡电力供应和需求。文献[5]分析了可再生能源和电动汽车的虚拟电力市场,提出了一种基于多智能体系统(Multi-Agent System,MAS)的充电规划模型。在电动汽车峰值调度方面,文献[6]将连接的电动汽车电池作为储能装置,并使用改进优化算法求解最优调度方案。文献[7]研究了电动汽车储能特性,侧重于电网的安全运行情况提出电动汽车和分布式能源共同参与的电网互动策略。本文以居民区低压变电站区域为应用场景,以总负荷方差最小和调度成本最小为主要优化目标,研究电动汽车在特定应用场景下的调度方案。

1 EV充电负荷预测

1.1 用户充电行为特性

以传统燃油汽车出行特性代替电动汽车出行特性,由家庭出行调查结果可拟合得到EV起始充电时刻的概率密度函数[8],即

(1)

式中,μ、σ分别为函数期望值和标准差;t为充电起始时刻,家用电动汽车充电起始时刻满足N(17.6,3.42)。

EV起始荷电状态(State of Charge,SOC)指电动汽车起始充电时刻的电池容量所占电池总容量的百分比,是计算电动汽车充电时长的前提[9],电动私家车起始充电时刻满足N(0.5,0.12)。根据EV起始荷电状态SOC可得充电时长Tc,即

(2)

其中,SOCe、SOCi分别为EV目标期望荷电状态和起始充电荷电状态,一般SOCe=1;E为电池容量,单位为kWh;Pc为充电功率,单位为kW;η为充电效率,一般为0.9。若已知EV充电起始时刻和充电时长,即可得到充电时段。

1.2 基于蒙特卡洛算法的充电负荷预测

蒙特卡洛算法(Monte Carlo Method,MCM)是一种基于概率论与数理统计知识的模拟算法。MCM求解随机事件的核心思想就是通过大量的不确定试验来求解某个随机事件发生的概率,进而求出最终期望值[10]。根据MCM模拟算法进行大量随机试验,由起始充电时刻的模型来生成起始充电时刻的随机数,计算统计参数,模拟出EV的充电行为求出其充电负荷,EV充电负荷计算方法如图1所示。

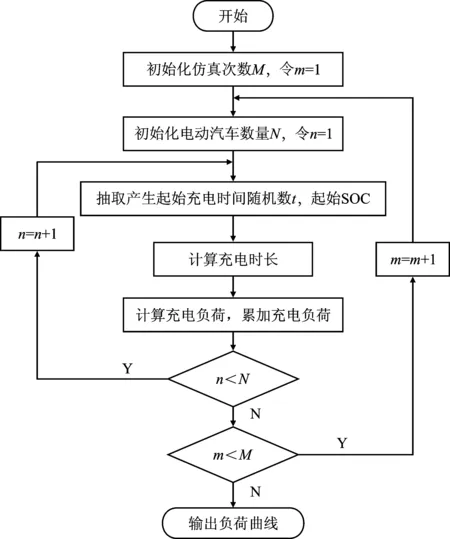
图1 EV充电负荷的计算流程Figure 1. Flow of EV charging load calculation

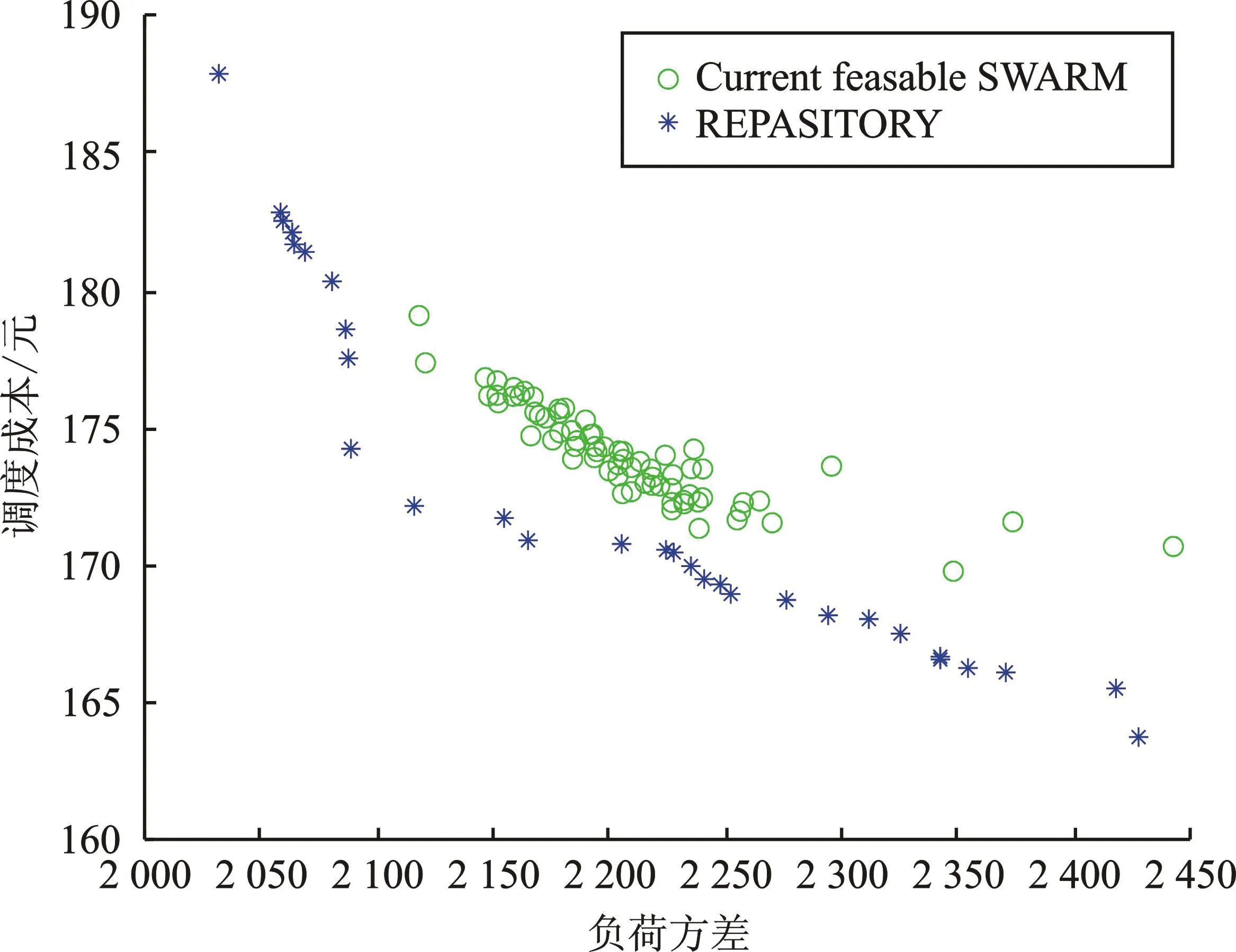
图2 多目标调度Pareto最优解 Figure 2. Optimal solution of multi-objective scheduling Pareto

2 调度模型

V2G技术是EV有序充电重要保障,在集中式V2G方式下,EV集群拥有更多的可用充放电容量,便于管理[11]。本文所研究的调度系统包含EV用户、调度系统运营商和电网公司、主要相关设备包括电动汽车、V2G设备、配电网(主要指低压变压器)等。电网公司作为电力供应商,负责充电需求和居民用电需求,稳定负荷是主要目的[12]。对EV用户而言,其主要目的是在不影响日常出行需求的前提下以充电成本最小为佳,由此将调度策略研究目标为电力系统负荷方差和系统调度成本。

2.1 目标函数

本文在保证配电网安全稳定运行下[13],以运营商系统调度成本最小和电力系统负荷方差最小为优化目标。其数学模型可概括为多目标、多约束问题[14],可描述为

(3)

式中,x=(x1,x2,…,xn)为n维决策向量;fk(x)为第k个目标函数;gi≤0为q个不等式约束条件;hj=0为p个等式约束条件。

(4)

(5)

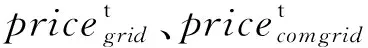
在EV放电时,运营商向EV用户支付成本为

(6)

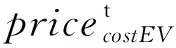
对EV用户而言,V2G技术的应用使其充电成本降低。本文主要研究以运营商为主题的系统调度成本,包含购电成本和放电成本。由以上分析可知,目标函数可描述为:

1)电力系统负荷方差

(7)

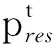
(8)

2)系统调度成本最低

(9)

2.2 约束条件

1)EV充放电功率

(10)

其中,pmax ch、pmax dch分别为EV在充放电过程中充电功率上下限。

2)电池SOC

(11)

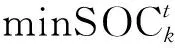
3)系统总功率

(12)

其中,α为变压器效率;ST为变压器额定容量

3 多目标粒子群算法求解模型

3.1 多目标粒子群

多目标优化问题最优解不具有唯一性,各个目标之间相互制约[15],难以用某个标准判断定粒子的位置是否为最佳位置。多目标优化问题的解是一组独立解是一个集合,称为Pareto前沿或非支配集,该集合在空间上表现为线或面。在实际工程应用中,可依据意愿在Pareto前沿中选择一个或多个作为问题的解[16-18]。多目标优化算法的目的是寻找到Pareto最优解。

粒子群优化算法具有规则简单、易实现等优点,本文采用多目标粒子群算法求解多目标电动汽车充电负荷有序调度问题。

3.2 模型求解流程

本文控制方案为改变EV接入的起始充电时刻以进行有序充电,因此多目标粒子群算法中的基本粒子为EV的起始充电时刻,即x=[t1,t2,…,tn],tn为第n辆EV起始充电时刻。

多目标粒子群优化算法流程如下:

1)运营商信息系统数据采集输入。由EV装载的车辆信息系统来获取接入车辆的信息,其中包括电动汽车电池的容量、充电功率大小等,由满足的概率分布模型随机产生所有电动汽车的起始荷电状态、起始充电时间。

2)初始化种群。确定种群维数、个数和迭代次数,初始化粒子的位置和速度,粒子初始个体最好位置为粒子本身。

3)计算初始种群适应度值,个体的适应度值有两个,即电力系统负荷方差和系统调度成本,同时个体需满足约束条件。

4)确定个体历史最优值,比较其与适应度函数值,更新个体最优值。

5)确定全局历史最优值,比较其与适应度函数值,更新全局最优值。

6)粒子速度更新和位置更新。

7)根据支配关系进行最优值更新。

8)对新的非劣解集进行更新并存档。

9)判断是否达到最大迭代次数,若不满足则返回步骤3,若满足则循环结束,输出Pareto最优解集合,得到EV有序充电的方案。

4 仿真与分析

4.1 仿真参数设置

为验证本文所提方法的有效性,以上海某配电区为例,变压器额定容量为500 kVA,适用于140户家庭,其EV数量为70辆,按照本文所建模型进行仿真求解。EV电池荷电状态最小值为0.3,充放电上下限均为7 kW,电池容量为45 kWh,百公里耗电量为15 kWh。多目标粒子群算法中其参数设置为:ω=1,c1=c2=2,种群个数100,最大迭代次数200,粒子维数等于EV数量70,每个粒子代表EV充电起始时刻,其取值范围为EV停车时间,从停车时间范围选取符合目标函数的最优起始充电时间。该地区日常居民电价如表1所示。

表1 某地区日常居民电价Table 1. Daily residential electricity price

4.2 仿真结果分析

对本文所提模型进行仿真计算,由MPSO算法粒子找到Pareto前沿解集如图3,符号“*”表示Pareto前沿,“○”表示当前可用种群。可以看出,Pareto前沿较均匀在空间中,Pareto前沿中,当负荷方差减小时,调度成本增加,同时说明多目标优化问题中不同目标函数之间矛盾。本文按照在区域负荷变化的可接受的情况下选择调度成本最低的解,因此最终选择负荷方差为2 428,系统调度成本为163.7元的充电方案。在此方案下,可得EV起始充电时间概率分布如图4所示。

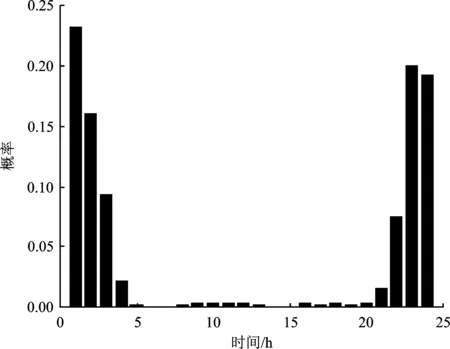
图3 有序充电时电动汽车的起始充电时刻分布Figure 3. Distribution of initial charging time of electric vehicles during orderly charging

图4 不同EV数量下系统负荷峰值比较Figure 4. Comparison of system load peak value under different EV numbers

图3表示在本文所提调度模型下,EV起始充电时刻主要集中在21∶00～24∶00和次日0∶00～04∶00阶段,相较以往居民返回家里立即充电(主要集中在17∶00～20∶00)具有较大改变。由表1可知,夜间电价也普遍较低,对EV用户来说,也降低充电成本。

由图5可知,随着调度系统区域内EV数量的增加,在无序充电的情况下,区域内系统总负荷的峰值随着电动汽车的增加而线性增加,而应用本文所提方案有序充电,系统总负荷波动不大。其次,当参与调度系统EV数量为10和30时,总系统负荷峰值分别为89.69 kW和95.21 kW,已知该区域基本日常负荷的峰值(98.5 kW),由此可知,一定数量EV参与调度系统,不仅不会增加系统负荷峰值,还具有一定调峰作用。

表2列出了不同EV数量下系统负荷峰值,在该区域内EV数量增加到50辆和70辆时,在调度系统作用下,总系统负荷峰值分别增加到108.60 kW和137.60 kW,与居民日常负荷峰值相比,用电量峰值分别增加10.2%和39.7%。相同数量的EV无序充电情况下,峰值分别增长125.9%和180%,可以看出本文所建立调度系统模型对稳定总电力负荷具有显著影响。

表2 系统负荷峰值比较Table 2. System load peak comparison

5 结束语

为减轻EV负荷无序充电对电网的不利影响,本文考虑EV的充放电特性提出了一种多目标优化有序充电调度策略,建立了考虑调度成本和系统负荷波动方差的多目标优化模型,通过粒子群算法对模型进行求解。仿真结果表明,本文所建立调度模型能够有效减少无序充电对配电网不利影响,降低负荷峰值,同时对于EV用户也可以将充电成本缩减。在今后的研究工作中可针对粒子群算法中惯性权重问题进一步优化。