多核处理器中混合关键级任务可调度及半分区划分算法

朱嘉炜,冒 航,张凤登

(上海理工大学 光电信息与计算机工程学院,上海 200093)

多处理机调度分为划分调度、全局调度以及半分区调度。全局调度允许所有任务在任意处理器之间不受约束地进行迁移,而分区调度在任务进行调度前对所有任务根据相应的规则进行物理区域上的划分,每个任务只能在相应的处理器上被执行。相比于全局调度和划分调度算法,半分区调度算法能够较好地克服处理器利用率低和系统资源开销大等问题,而优秀的半分区划分算法能够使得整个系统在任何情况下都具有较好的容错性和执行性[1]。在混合关键级系统中,任务的分区划分需要考虑不同任务的关键级以及任务之间的相关性。文献[2]通过对每个核计算性能并赋予其不同的权值来进行任务分区划分,提出WRR(Weighted Round-Robin)算法。文献[3]基于EDF(Earliest Deadline First)算法提出负载均衡策略用于半分区划分调度。文献[4]提出高性能任务切分算法MC-EKG(Mixed-Criticality-EKG)。

1 半分区动态需求边界函数分析法

对于半分区划分调度算法,在任务调度前和任务划分后需要进行可调度性分析[4]。较佳的可调度性分析法可提升算法对任务集任务接收的数量,且对于MCS(Mixed-Criticality System)系统来说,普通的可调度性分析法效果并不好。CPU利用率边界法在动态优先级的调度算法中,理论上界为100%,但在实际调度过程中无法达到该上界,实用性并不高。文献[5]对DBF(Demand Boundary Function)分析法进行改进,提出一种单核平台的混合关键级动态需求函数DDBF,用以在MCS的动态优先级调度算法中分析任务集的可调度性。

本文主要研究DDBF并根据半分区划分调度算法框架进行改进,针对多核处理器进行了DDBF的应用扩展,并在考虑结转作业、前接作业的影响后,给出了不同关键级任务在不同系统关键级下的动态需求边界函数SDDBF,基于SDDBF提出了SDA可调度性分析法。

1.1 DDBF组成

在关键等级x时,一个任务τi的时刻t完整的执行需求,主要考虑两种情况:

2)作业已经就绪,在此时的执行需求时间即为它在当前关键级x下对应的执行时间Ei(x),即

(1)

此时任务τi的作业被任务τj的作业阻塞情况为:任务τi作业的优先级比τj低,并且τj的关键级不低于当前系统的关键等级x。若低于系统的关键等级,τj将会被降级处理甚至抛弃,无法对处于当前队列的任务作业造成阻塞。因此阻塞时间是此时τj的WCET(Worst Case Execution Time),即

(2)

1)任务的达到时间ai。

周期任务指按一定周期到达并请求运行的任务,本文规定其在系统初期创建且初始化完成,作业Ji,j的到达时间就是任务τi的周期。

ai=Ti×(j-1)

(3)

在混合关键级系统运行时,每个作业的WCET值均会被关键级的变化所影响。一旦有一个作业的执行需求发生改变,后续的高关键级任务的作业均会被影响,进而影响到分配给每个作业的动态需求边界值。在半分区划分调度算法的调度模型中,在模式切换后会对低关键级任务作业进行回收,对回收的作业进行处理然后找到合适的时间重新执行或者直接抛弃。但是这些行为的前提是不得影响高关键级任务的执行。本文提出的方法在保证高关键级任务作业的动态需求边界的同时降低关键级任务作业缩减服务质量,并利用两类空闲时间处理。

假设作业Ji,j在关键等级x时的执行时间是Cj(x),但是在执行该作业时系统的关键等级变化至xo,此时它的执行时间变为Cj(xo)(Cj(x)≥0),因此对于作业Jj,k,其作业需求变化差值为

(4)

根据上述4点,给出如下定义:

定义1当系统关键等级为x时,一个周期任务τi在t时刻的动态需求边界函数如式(5)所示。

(5)

1.2 改进的动态需求边界函数SDDBF

由于DDBF是单核处理器的资源需求计算函数,因此需要考虑其是否可应用于多核环境和应用时与单核情况下的不同之处,以及用在半分区划分调度算法中需要注意之处[5-6]。

1)一旦发生系统关键级提升,一直到下一次关键级回落,低关键级任务都不会对高关键级产生任何阻塞。对于回收低关键级任务的算法来说,需要考虑低关键级任务的阻塞情况;

(6)

2)在多核混合关键级调度运行过程中,任务的执行情况会受到其他分区任务的影响。例如在第1个分区中高关键级任务执行失败触发了系统关键等级的提升,此时其他分区上正在执行的低关键级任务将被立即抛弃,剩余执行需求将被直接无视。本文将这段阻塞的部分作业命名为前接作业,其造成的阻塞为

(7)

式中,Ck(xo)为关键等级变化前的执行需求;Ck(ts)为系统关键等级改变时刻已经执行的部分,可以通过SDDBF函数计算得到。

DDBF并未考虑到任务抛弃后的回收行为,本文需要考虑任务作业回收的情况。假定低关键级任务作业Ji,j重新到达时间就是关键级发生变化的时间ti

(8)

式中,n为重新到达后的执行次数;ti为低关键级任务的周期;LO为低关键级;HI为高关键级。

综上给出如下定义:

(9)

除了上述的变化,在多核处理器的MCS中,当发生关键级切换时,每个核的运行状态较复杂[7-8],需要综合考虑多个分区(核)各自的运行状况。

前接作业是由于其他分区触发关键等级提升而被动产生的作业。记触发系统关键等级提升的分区为UP-Partition,该分区也会产生一种作业,称之为结转作业(Carry-Over Jobs)。

如果分区UP-Partition上的高关键级任务作业触发了系统关键级的切换,意味着分区UP-Partition的高关键级任务τi的作业Ji,j在此时只执行了一部分却被迫中断,仍有n个时间单位需要运行,而这n个时间单位需要在l个时间的剩余资源窗口内执行完成。这个剩余资源窗口即为模式切换时刻ts到作业Ji,j的实际截止时限Di的差值。当模式切换后,执行需求n至少执行了max{Ci(LO)-l,0}个时间单位,因此作业Ji,j的执行需求n至多为变更后的总执行需求减去已经执行的需求,即Ci(HI)-max{Ci(LO)-l}。

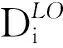
图1 时的结转作业Figure 1. Carry-over jobs when

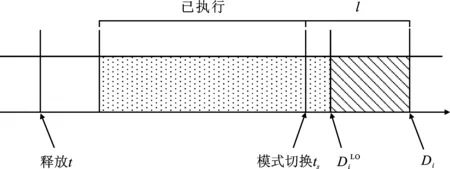
图2 时的结转作业Figure 2. Carry-over jobs when

(10)

若发生更坏的情况,导致新增需求后无法在截止期前完成,那么将不可调度。当系统关键等级提升后,一个严格触发系统关键等级提升的分区结转作业的动态需求函数为

(11)

对于本文混合关键级半分区的任务作业来说,原本可以在截止期前完成任务,因为其他分区触发了系统关键等级的提升导致动态需求增加,超过其截止期限,最终存在不可调度的情况。

上述计算式适用于本文半分区系统模型中的任一分区,且主动触发关键级模式提升的分区UP-Partition是高关键等级任务的作业。因此对于结转作业可以得到一个如下所示的计算式。

(12)

表1 例1任务集属性Table 1. Example 1 task set properties

例1最终的动态需求边界函数如图3所示。系统在一个时刻仅存在一个关键等级的可能,所以图3仅用任务作业区分,同一作业在不同关键级下的动态需求值用同一根线表示。

1.3 可调度性分析

根据式(8)和式(9)可以引申出可调度性定理:

定理1当系统关键级处于x时,任务τi在时刻t某个作业能被调度的条件是

(13)

定理2当MCS关键级处于x时,任务τi能被调度的条件是

(14)

(15)

本文动态需求边界函数算法的细节为:本质就是对于任务τi在时刻t需要的资源与此时刻该任务所在分区的剩余资源关系,它是一个离散时间的动态函数,在每一个事件的时间点计算当前队列中任务的动态边界需求函数与每个分区的总资源与剩余资源。绝大部分任务的周期小于超周期mlcm,可能一个超周期mlcm包含任务τi的多个作业[10]。该可调度性分析法使用定点动态需求分析法,在确定任务集后,生成所有任务的截止时间,直接计算各个截止时间点的动态需求值,依次判断各个时间点上任务作业的可调度性[11]。

由于本文的系统模型为多核处理器的半分区模型,因此只列出一个分区的任务集的可调度算法,伪代码如下所示。

算法1 可调度性测试算法SDA输入:划分至区的任务集Γ=τ1,τ2,τ3,…,τn ,超周期mlcm=lcmT1,T2,…,Tn 。输出:任务集Γ的可调度性判定。1.For t from 0 to mlcm do /*任务数量*/ 2. for i from 1 to n do /*系统关键等级*/3. if Ls = LO4. if t== GetCur_PeriodDead(τi)5. Calcluate SDDBFLOit ;6. if SDDBFLOit > GetCur_PeriodDead(τi)7. return “τi is not schedulable”8. end if9. end if10. end if11. if Ls = HI && Li=HI12. if t== GetCur_PeriodDead(τi)13. Calcluate SDDBFHIit 14. if SDDBFLOit > GetCur_PeriodDead(τi)15. return “τi is not schedulable”16. end if17. end if18. end if19. end for20.end for21.return(“schedulable”);

该可调度性分析法对每个周期任务作业的截止期进行判断,判断该作业在当前周期内能否被满足其SDDBF值,满足即为该作业可调度,从而得出整体任务集可调度性的情况。对于高关键级任务来说,需要判断其在LO、HI模式下的可调度性。对于整个任务集来说,所有区间的任务均可以被调度,才可认为整个任务集完全可调度。SDA分析法在分析过程中使用的优先级判定即为调度算法的优先级判定方法。

2 基于SDDBF的半分区划分算法

划分算法有利于各分区间负载均衡,对于MCS来说,避免分区间负载差距过大,使得系统触发关键等级提升的次数减少,也能使得系统在各个模式下都有较为相近的处理器利用率。文献[12]改进了WF(Worst First)、BF(Best First)划分算法,提出了WF_MY、BF_NEW(Best First_New)、WF_NEW这3个算法,其中预测性划分算法WF_MY综合性能最好。本文对WF_MY划分策略进行改进,基于SDDBF动态需求边界函数提出更适合MCS的划分策略,为后面章节的算法提供划分策略。

2.1 WF_MY划分策略

划分算法WF_MY通过改良WF算法得到,它在划分任务时会考虑到下一个任务的划分,而不仅是当前的任务,该预测性做法使它可以较为均匀地分配任务。其伪代码如下所示。

算法2 WF_MY划分算法输入:待划分任务τi,处理器个数n。输出:任务的划分结果。1.for i from 1 to n2. for k from 1 to L3. Uik =∑Lx=kUixk +ujk 4. Eik =1-Uik 5. end for6. Uimin=minEi1 ,Ei2 ,…,EiL 7.end for8.Uiminmax=maxU1min,U2min,…,Unmin 9.cpu=i10.return CPU

算法步骤如下:

1)排序。将任务集按照任务自身关键等级最低的执行时间计算任务的利用率,然后按照该利用率由高到低排序;

3)任务划分后进行可调度性检测。基于系统资源利用率边界分析法,在划分任务时选用任务在最低关键级下的任务利用率,预测性地考虑为下一个任务预留资源。但是这样只考虑了单个关键级进行划分,在关键等级变化时,CPU 各个分区的负载均衡较难得到保障。

2.2 划分策略改进

WF_MY试图从关键级入手对划分算法进行调整,能对MCS进行效果较优的划分性能。但是仅因为高关键级模式触发次数少、时间不长就忽视,不在划分时做真正改变,这无法使得系统在各个关键等级下的各分区负载均衡。本文真正地考虑了均衡系统在各个模式下的负载。

本文对其进行改进,针对双关键级系统提出了MCWF算法。

步骤2按照贡献率排序依次划分任务,计算单个任务在超周期中所有作业SDDBF值之和作为划分依据,采用WF方式进行划分。

在步骤2中,划分任务的依据是分区中所有任务作业的SDDBF总和。但是对于高关键级任务来说,还会考虑在HI模式下,每个分区中高关键级任务的SDDBF总和。高关键级任务优先考虑在HI模式下的SDDBF值,在低关键级任务划分时,考虑每个分区中的所有任务在低关键级下的SDDBF值。本文采用窗口动态需求边界函数,计算窗口时间内的执行需求上限。

算法3 基于 SDDBF的划分算法MCWF输入:待划分任务集Γ=τ1,τ2,τ3,…,τn ,系统超周期mlcm=lcmT1,T2,…,Tn 。输出:任务集Γ的划分结果。1.Priority(Γ);2.for i from 1 to num(τ)3. if Li==HI4. Calculate theSDDBFW,x i of τHIi;5. P=Get_Partition_SDDBFHI; /*所有分区中SDDBF值总和最小的分区*/6. UpdateSDDBFpmax7. ifSDDBFpmax>mlcm8. return “Allocate Failed”;9. else10. return P;11. end if12. if Li==LO13. Calculate theSDDBFW,x i of τLOi;14. P=Get_Partition_SDDBFLO;15. Update SDDBFpmax16. if SDDBFpmax>mlcm17. return “Allocate Failed”;18. else19. return P;20. end if21.end for22.return All Partition Result

在进行分区划分时并不涉及任务及作业的调度,不需要考虑任务间的抢占、阻塞等情况,需要对比各个分区中执行需求的总和。该方法适用于多关键级的系统。

伪代码第1行将任务进行EDF算法的截止期优先级计算方式排序,第2～11行是对高关键级任务的分区。第12～20行是对低关键级任务的分区。两者分区都是参考任务自身的关键等下分区的最大SDDBF值,这样做能使得各个模式下的 CPU 分区负载更均衡,从而使得算法不考虑迁移高关键级任务。该思维也可以用于多关键级任务:划分关键等级为x的任务时,考虑系统在关键等级x下,各个分区的SDDBF值。

2.3 WF_MY划分策略

为了体现MCWF算法在MCS中的优势,本文选取WF_MY与WF_NEW这两个同类型的算法进行比较。WF_NEW是WF算法的改进,其大致步骤与WF_MY相似,区别在于不会为下一次任务预留资源,比对不同关键等级下的利用率后,直接分配至剩余利用率最低的核。

例2一个包含8个任务的任务集,分别包含4个高低关键级任务,将划分至一个双核处理器。

3种划分对表2任务集的划分结果如表3所示,表2中的任务顺序即为分配时的顺序。为了方便比较,本文将各个算法的指标进行了转换、统一,将MCWF的SDDBF总和指转换为对应的利用率总和,将WF_MY与WF_NEW的利用率总和转换为对应的SDDBF总和。在这里可以清楚看到MCWF划分法划分出来的任务,在HI、LO模式下的负载都较为相近,均衡性明显优于另外两个划分算法,它使得核1与核2的SDDBF总和、利用率总和的差值处于一个较小的水平。

表2 MCS划分任务集Table 2. MCS divides the task set

表3 各算法划分结果Table 3. Each algorithm partition results

表4 各算法划分结果(上表续)Table 4. Partitioning results of each algorithm (continued in the above table)

3 仿真测试

本文针对混合关键级半分区的动态需求边界函数分析法进行任务集的实际测试与划分算法MCWF的对比测试。

3.1 可调度性测试

可调度性测试的对比算法为AMC、AMC-max,XU[13]在双关键级系统中采用半分区划分调度算法,在划分任务后使用AMC相关响应分析法对分区上的动态优先级任务进行可调度性分析,通过依次分析各个分区的可调度性来判断整体的任务集可调度性。

AMC可调度性分析原本是提出用于固定优先级任务集的可调度性分析,相比传统响应时间分析法,该方法去除了部分不必要的悲观因素。考虑MCS在系统关键等级切换时刻任务的需求,将响应时间内的阻塞时间段分细分,包含了低、高关键级任务的高优先级作业,且将低关键级任务造成阻塞时间的计算缩减。

由于任务集设定是隐式截止期Di=Ti,且是到达时间固定的周期任务,因此在没有外界干扰的情况下,每一个周期内的执行结是一致的。所以本文选择观察一个超周期内的作业执行情况。

本文的任务释放时间均为0,参考实际项目参数值并使用UUnifast[14-16]算法生成,使用的任务参数设置如下:

1)任务的Ci:每个任务作业的最坏情况执行时间。高关键级任务的Ci为向量,双关键级系统下为Ci=(Ci(LO),Ci(HI)),低关键级任务作业的Ci在双关键级系统下为Ci(LO);

2)任务关键级Li:一个系统中高关键级任务实际占少数,大部分是功能安全性相对不高的任务与功能,但是也可以通过改变该参数的比例反映可调度性算法的真实有效;

3)任务截止时限Di:任务作业最晚需要在这个时间点完成,本文为隐式截止时限,Di=Ti;

4)周期Ti:任务作业的到达间隔,本文为了实验的精度,对所有数据进行了放大,周期取值为100×Basetime,Basetime∈[1,64]。Ti值需要考虑作业之间的阻塞情况,其区间分布数量随周期长度递增。任务集的超周期为任务周期的最小公倍数,为了防止该最小公倍数过大,Ti的取值需要具有一定规律性及合理性。

最终将生成单个任务利用率在[0.000 5×m,0.015×m]区间,测试任务集确保其平均利用率Uavg∈[0.2,1],任务数量为TaskNum初始选择 100。对于本文MCS来说,平均利用率为Uavg,代表任务集在高、低关键等级下的利用率之和的均值,再以该均值对核的数量取平均的值

(16)

选择系统规范化利用率作为控制变量,取值[0.05,1.00],高关键级任务占比CP为0.3。观察可以成功调度的任务数量以及被成功调度任务的利用率之和,越接近1说明算法的调度越好。

结果如图4所示,Umax是非固定优先级调度算法的理论利用率上界,理论值恒为1。采用SDA进行可调度性分析比使用响应时间分析的AMC-rtb(Adaptive Mixed Criticality for response time bound)、AMC-max要高出 10%～30%。考虑了混合关键级系统的模式切换特性,考虑了结转作业、前接作业,对时间的计算与分配更加精准,更适合会触发关键级切换的MCS。

图4 任务集平均利用率Figure 4. Average task set utilization

3.2 划分算法测试

MCWF的对比算法为WF_MY与WF_NEW,测试方法与可调度性测试一致,通过生成随机性任务集进行测试。

由于对同一个任务集而言,在划分算法固定的情况下,划分结果也固定,为了能够观察出算法间的差距,本文测试选取的平均利用率为 70%,高关键级任务占比CP为50%任务集的任务数量由100降为 40,共进行100次任务集的随机生成与测试[17-18],其余参数设定均遵循上节的可调度性测试。

本文验评估指标选择同一个平均利用率下各分区的划分结果值方差,分别为高、低关键等级下的SDDBF值方差与利用率方差,所有方差值均为100次实验后的总平均值,取小数点后一位[19-20]。

从表5可以看到,MCWF的划分结果在高、低关键等级下都较为相近,相比于WF_MY、WF_NEW,其划分效果有一定的提升,尤其是对于高关键级任务的均分具有明显优势。

表5 各划分算法方差Table 5 The variance of each partition algorithm

4 结束语

本文基于动态需求边界函数SDDBF结合混合关键级半分区算法模型进行具体的改进性分析,并给出了可调度性分析法SDA,最后与AMC、AMC-max进行可调度性实验,观察不同CPU平均利用率的可调度性分析结果,确定动态需求边界函数可调度性分析算法的有效性。并提出了基于 SDDBF的半分区划分算法MCWF,相比一些基于传统改进的划分算法,该方法具有良好的划分效果。

从实际应用角度对可调度性分析法SDA的效果进行分析。随着防抱死系统(Anti-lock Bracking System,ABS)、电子制动力分配(Electronic Brake Force Distribution,EBFD)、自动泊车系统(Automated Parking System,APS)等功能的加入使得汽车电子系统愈发庞大。单核处理器早已无法满足这样的需求,而本文提出的基于多核处理器的SDA可调度分析方法能够更好地为这些需求提供服务。例如当前消费者更加注重音乐、视频等功能,SDA可调度性分析能够使得这些功能的完成率更高,最终提高消费者的驾驶体验。

综上所述,从理论和实际角度考虑,本文提出的SDA可调度分析方法,都具有一定的意义。