信道衰落下多智能体系统有限时间一致性控制

丁 勐,陈 蓓

(上海工程技术大学 电子电气工程学院,上海 201620)

多智能体系统(Multi-Agent Systems,MASs)由多个带有自治性的智能体组成,其目标是将复杂系统构建成易于管理、智能体之间能够进行通信和协调作业的系统。随着网络通信与控制技术的不断进步与融合,多智能体系统已经发展为复杂系统分析与模拟的重要思想方法与工具,研究内容涉及智能体的目标、技能、规划以及让智能体之间采取协调一致的行动来完成任务。近年来,多智能体系统在编队控制[1]、水下协同控制[2]以及无人机集群控制[3]等领域得到了广泛应用。

一致性问题[4-8]是多智能体系统中协同控制领域的基本问题。为解决多智能体系统一致性问题,学者们提出多种控制方法,包括预测控制[9]、自适应控制[10]、模糊控制[11]以及滑模控制[12]等。其中,滑模控制凭借对外界干扰和参数不确定性的强鲁棒性,在多智能体系统一致性问题中得到了学者的广泛关注[13-15]。文献[14]研究有向拓扑网络中二阶多智能体系统的固定时间一致性跟踪问题,针对双积分器多智能体系统设计了滑模面并在其基础上构造非线性一致性协议。文献[15]针对机器人多智能体系统的一致性跟踪问题提出了一种基于投影递归神经网络的最优滑模控制技术。

在控制领域中,度是评价系统性能的一个重要指标。对于多智能体系统而言,实现有限时间一致性跟踪具有显著的实际意义。根据达成一致性的收敛速度,可分为渐进一致性[16]和有限时间一致性[17-19]。在文献[20]搭建的多智能体系统中,当时间趋向无穷大时,一致性跟踪误差会根据设计的滑模控制律到达指定的滑模面,然后沿着滑模面移动,最终收敛到0。与渐进一致性相比,有限时间一致性要求系统的状态在有限时间内收敛到指定范围。为确保有限时间一致性跟踪,文献[21]提出了一种分布式非奇异快速终端滑模方法来加快系统的收敛速度,并且给出了达到一致性的时间上界。

但是,上述工作大多基于理想的网络通讯环境,即信息可以在智能体之间完整传输。实际上,在网络通信下,不可避免地存在时滞和随机干扰等因素的影响,难以保证理想的通信环境。近年来,信道衰落下多智能体系统的一致性问题开始受到关注。文献[22]分别对不同数量智能体系统进行讨论,建立信道衰落模型,根据固定拓扑下的仿真数据得到信道衰落对于多智能体系统一致性的影响。文献[23]设计了一种分布式控制器以解决具有信道衰落现象的离散时间多智能体系统一致性问题。

本文针对信道衰落下二阶多智能体系统的有限时间一致性控制问题,根据从邻居智能体接收到的衰落数据得到一致性误差函数,构造非奇异终端滑模面,提出一种有限时间一致性控制策略。在该策略作用下,误差函数的状态将在有限时间到达并保持在所设计的滑模面上,最终实现多智能体系统的有限时间一致性跟踪。

本文采用的数学符号:Rn和Rm×n分别表示n维的欧式空间和m×n的实矩阵集,⊗表示Kronecker积,sgn(x)表示符号函数,符号|·|和‖·‖分别表示欧几里得范数和向量范数,1N=[1,1,…,1]T,0N=[0,0,…,0]T。

1 问题描述

1.1 图论基础

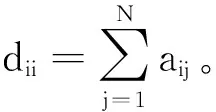
1.2 系统模型

由一个领导者和N个跟随者组成二阶多智能体系统,其动力学模型为

(1)

其中,xi(t)∈Rm、vi(t)∈Rm、ui(t)∈Rm、fi(t)∈Rm分别为第i个跟随者的位置、速度、控制输入和扰动;x0(t)∈Rm、v0(t)∈Rm、u0(t)∈Rm、f0(t)∈Rm分别为领导者的位置、速度、控制输入和扰动。

假设1假设式(1)中的干扰fi(t)和f0(t)满足Lipschitz条件(干扰上界μ为Lipschitz常数)

‖fi(t)-f0(t)‖≤μ‖vi(t)-v0(t)‖

(2)

为了实现多智能体系统的有限时间一致性,定义第i个跟随者的一致性误差函数为

(3)

其中,ε1i(t)和ε2i(t)分别为跟随者的跟踪位置和速度误差状态变量;aij为邻接矩阵A中的一个元素;领导者的度矩阵hi决定了领导者和跟随者i之间是否有信息交互,hi>0说明跟随者i可以接收领导者发送的信息。

将一致性跟踪误差简化为紧凑形式

(4)

H≜diag(h1,h2,…,hN)。

对式(4)求导得到

(5)

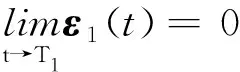
1.3 信道衰落模型

由于时滞、随机噪声等干扰因素的影响,信息在跟随者之间传输不可避免地受到信道衰落影响。考虑到追随者之间传输信号的振幅大小可能受到随机干扰,网络信道可以视为具有增益的连续信道。

假设2本文考虑的信道衰落现象只发生在跟随者的信息交互中,假设领导者和跟随者之间的信息传递过程中不存在衰落现象。

考虑如下衰落模型

(6)

基于式(6)的信道衰落模型,推出式(3)为

(7)

其中,Λ1(t)≜diag(0,φ12(t),…,φ1N(t)),…,ΛN(t)≜diag(φN1(t),φN2(t),…,0)。

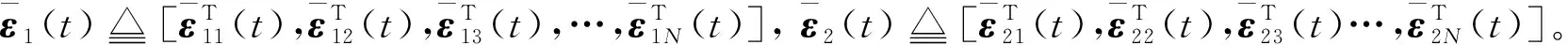
(8)

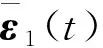
1.4 相关引理

引理1[24]如果有向图G存在有向生成树,则矩阵L+H可逆。

引理2Cp不等式:假设存在实数a、b和p,且p>0,则满足

(|a|+|b|)p≤Cp(|a|p+|b|p)

(9)

其中,Cp的值满足

(10)

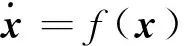
(11)

其中,0<β<1,c>0。则非线性函数f(x)是局部有限时间稳定,并给出关于初始状态x0的有限时间上界

(12)

2 主要结果

2.1 滑模面和滑模控制律设计

第i个智能体的滑模面函数设计为

(13)

其中,c和α均为标量且c>0,1<α<2。

将式(12)化简为紧凑形式

(14)

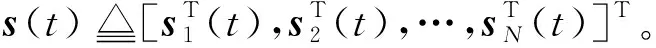
(15)

根据式(5)和式(15),得到式(14)导数如下所示。

(16)

由于信道衰落现象,智能体之间无法进行正常的信息交互,第i个跟随者无法从其他跟随者处接收到准确完整的信息,则信道衰落下的滑模面函数为

(17)

将式(17)改写为紧凑形式

(18)

设计滑模控制器如下所示。

(19)

本文提出了基于终端滑模控制的有限时间一致控制算法。在此控制算法下,多智能体的跟踪误差量可以在有限时间内到达设计的非奇异终端滑模面上,并沿着滑模面趋于稳定,保证多智能体系统的有限时间一致性。

2.2 一致性和可达性分析

本文基于构造的非奇异终端滑模控制律,借助Lyapunov函数方法分析在信道衰落现象下多智能体系统的一致性和可达性。

定理1考虑多智能体系统在信道衰落下,滑模控制器能够保证非奇异终端滑模面可达性。

证明构造Lyapunov函数

(20)

对式(20)求导得

(21)

根据式(19),得

(22)

由假设1,可知

‖f(t)-1N⊗f0(t)‖≤(‖fi(t)-1N⊗f0(t)‖),…,
(‖fN(t)-1N⊗f0(t)‖)≤
‖(μ‖vi(t)-1N⊗v0(t)‖),…,
(μ‖vN(t)-1N⊗v0(t)‖)≤
μ|‖(L+H)-1⊗ε2(t)‖

(23)

因此,由式(23)进一步推出式(22)如下所示。

(24)

对式(24)两边取数学期望,可得

(25)

根据上述关系式,代入式(25)可得

(26)

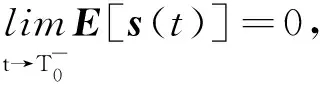
定理2考虑多智能体系统在信道衰落现象下,本文设计的滑模函数和滑模控制律能够保证多智能体系统的有限时间一致性。

证明构造Lyapunov函数

(27)

对其求导可得

(28)

当s(t)=0时,推出

(29)

根据式(29)和Cp不等式(引理2),有

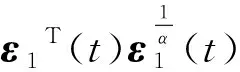
(30)

由式(30),可得

(31)

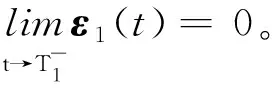
3 仿真分析

由1个领导者和4个跟随者组成二阶多智能体系统,其中智能体之间的通信拓扑如图1所示。

图1 多智能体系统的通信拓扑Figure 1. Communication topolopy of MASs

在图1中,实线表示跟随者之间的信息交互方向,且不存在信道衰落现象,信息可以完整传递,虚线表示跟随者之间的信息交互方向且存在信道衰落现象,信息传递过程中幅值衰减。假设智能体之间的邻接权值为1。

根据跟随者和领导者之间的拓扑结构可以得到该多智能体系统的邻接矩阵A、领导者的入度矩阵B和拉普拉斯矩阵L。

领导者的控制输入为u0=[cos(t),sin(t)]T,滑模控制器中的参数设计为c=1.0,k=0.1,α=1.5,扰动参数μ=0.1。领导者的初始位置和速度状态量为x0=[10,-10]T,v0=[10,-10]T,跟随者的位置和速度的初始值为:x1=[10,-2]T,v1=[20,-2]T,x2=[15,15]T,v2=[20,3]T,x3=[25,5]T,v3=[15,0]T,x4=[45,15]T,v4=[35,0]T。

仿真结果如图2～图5所示。其中,图2为多智能体系统在指定的滑模面和滑模控制律下的状态轨迹曲线。从图2可以看出,跟随者(i=1,2,3,4)可以准确地跟踪领导者,多智能体系统一致性达成。

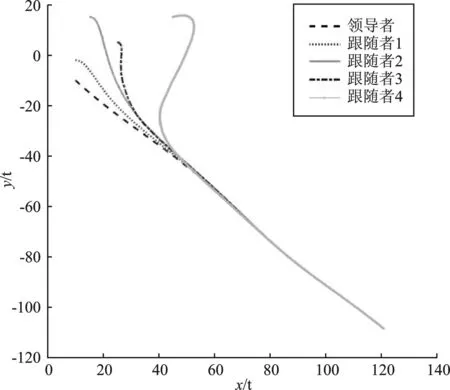
图2 多智能体的状态轨迹Figure 2. State trajectories of the multi-agents

图3和图4分别显示了每个跟随者的位置误差和速度误差函数轨迹曲线。其中,上标e1iq和e2iq分别为第i个跟随者的第q个状态量的位置和速度误差曲线。从图3和图4可以看出,位置误差和速度误差在有限时间内收敛。观察跟随者3和跟随者4,可以看出其位置误差和速度误差函数轨迹在收敛的过程中动态性能差于跟随者1和跟随者2,这是由于在信道衰落现象的影响下,跟随者3和跟随者4只能接收跟随者1和跟随者2发送的衰落信息,而跟随者1和跟随者2可以接受领导者的准确信息。图5为跟随者的滑模函数s(t)状态轨迹,其中,上标siq为第i个跟随者的第q个状态量的滑动变量曲线。其中,跟随者3和跟随者4的轨迹表明,虽然由于信道衰落影响下产生的震荡现象影响了跟随者3和跟随者4一致性达成的收敛过程,但本文设计的分布式滑模控制算法仍能克服信道衰落对系统的影响,最终多智能体系统的有限时间一致性得以保证。

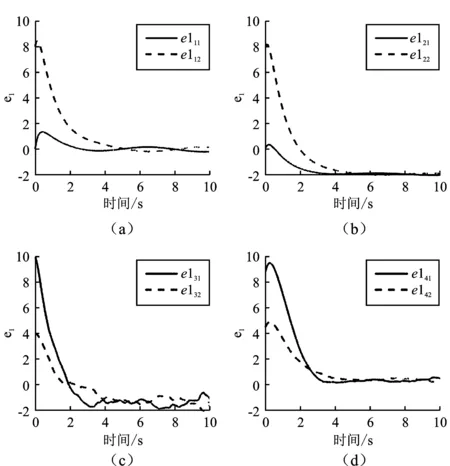
图3 跟随者的位置误差(a)跟随者1的位置误差 (b)跟随者2的位置误差 (c)跟随者3的位置误差 (d)跟随者4的位置误差 Figure 3. Position error of the followers(a)Position error of the followers 1 (b)Position error of the followers 2 (c)Position error of the followers 3 (d)Position error of the followers 4

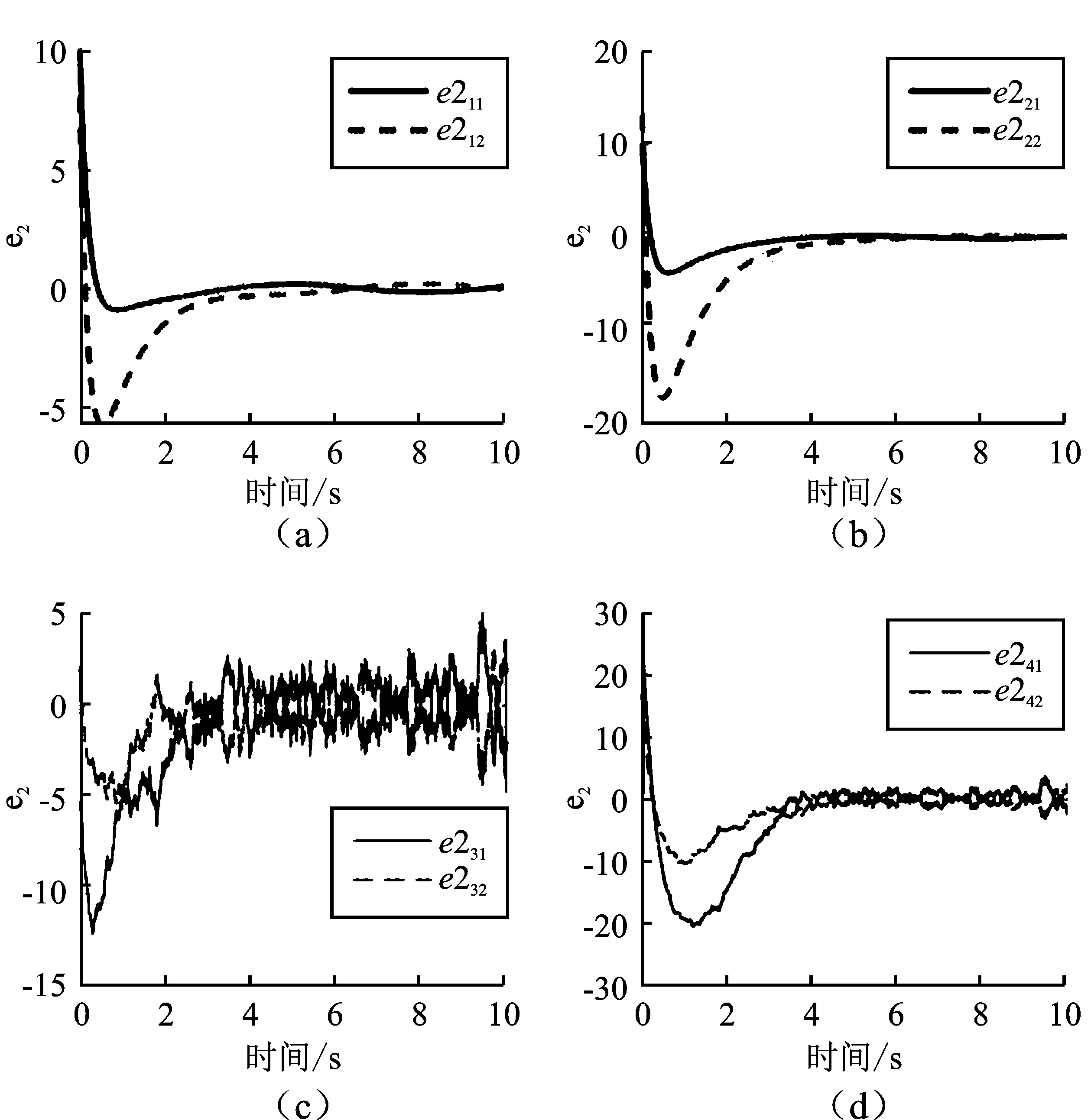
图4 跟随者的速度误差(a)跟随者1的速度误差 (b)跟随者2的速度误差 (c)跟随者3的速度误差 (d)跟随者4的速度误差 Figure 4. Velocity error of the followers(a)Velocity error of the followers 1 (b)Velocity error of the followers 2 (c)Velocity error of the followers 3 (d)Velocity error of the followers 4

图5 跟随者的滑动变量(a)跟随者1的滑动变量 (b)跟随者2的滑动变量 (c)跟随者3的滑动变量 (d)跟随者4的滑动变量 Figure 5. Sliding variables of the followers(a)Sliding variables of the followers 1 (b)Sliding variables of the followers 2 (c)Sliding variables of the followers 3 (d)Sliding variables of the followers 4

4 结束语

本文针对信道衰落下的二阶多智能体系统有限时间一致性跟踪问题提出了基于滑模控制的分布式控制算法。根据智能体的拓扑结构搭建了数学模型,基于误差函数设计一致性协议将系统的一致性问题转化为误差系统的稳定性问题。在此基础上,构造合适的Lyapunov函数,证明了滑模面有限时间可达性和多智能体系统的稳定性。最后,通过仿真实验可以看出该多智能体系统能够达成一致性,且过程中各智能体的动态性能存在显著差异,这是由信道衰落现象所引起的。