城市轨道交通连续支承轨道梁的动力响应分析

严志权，张 忠，华立夫，王天航，赵 俊

（1、广州地铁集团有限公司 广州 510320；2、中铁十九局集团第六工程有限公司 江苏无锡 214111；3、安徽建筑大学 合肥 230601）

0 引言

作为城市公交的骨干，城市轨道交通具有节能、省地、大容量、全天候、无（或少）污染、安全等优点，是一种绿色环保的交通系统，尤其适用于大中城市。但是，在列车行驶过程中由于列车与铁轨的耦合作用，会引起轨道周边环境及地上建筑的二次结构噪声，从而对建筑自身及周边人群的人身安全造成长远的不利影响［1］。所以，在城市轨道交通蓬勃发展的同时，列车行驶所引起的噪声与环境振动也引起了人们广泛的关注［2］。因此，对移动载荷作用下轨道梁的动态响应与力学特征进行研究也变得越来越有意义。

目前，关于移动荷载作用下梁的动力响应研究可以分为匀速移动荷载与变速荷载两类。在匀速移动荷载方面，ACHENBACH 等人［3］分析了无限长的均匀梁的解析解，得到了其在随载荷移动的坐标系中保持不变的结论；LEE［4］得到了Timoshenko 梁在Winkler 地基上的动力响应，并分析了其在忽略质量惯性效应的情况下承受等效移动力的相应行为；SUN［5］在21 世纪初提出了梁型结构对线荷载的闭式位移响应，进一步的，SUN［6］利用Fourier 变换结合Green 函数得到了梁在移动荷载作用下粘弹性路基上的闭式解；BASU 等人［7］计算了移动荷载作用下粘弹性地基上的Euler-Bernoulli 梁的解析式，并考虑了土壤中压缩应变引起的土壤阻力和剪切应变引起的阻力；HUANG 等人［8］采用双傅里叶变换和轮廓积分技术，得到了放置在Kerr 基础上并承受移动谐波荷载的均匀梁稳态响应的闭式解；ANSARI 等人［9］使用Galerkin 方法结合多尺度法（multiple scales method）得到了移动力作用下Euler 梁的频响曲线；胡伟鹏等人［10］利用了多辛算法的理论基础，针对移动荷载下梁振动的动力学方程提出了广义多辛算法理论；Mehmood 等人［11-13］则应用有限元方法数值地分析了移动荷载下梁结构的动力响应。然而，上述研究并未考虑荷载变速的情况。在变速移动荷载方面，王少钦等人［14］利用模态叠加原理，结合广义坐标变换的方法建立了变速移动载荷通过简支梁桥时的动力学方程并编写了分析程序；钟阳等人［15］基于Fourier变换，得到了弹性地基上无限长梁动态挠度和弯矩解析表达式；陈上有等人［16］建立了两种变速移动荷载下欧拉梁的动力分析模型，分别为车轮加弹簧-阻尼器-簧上质量和均布质量，推导了其振动控制方程；SUZUKI［17］利用菲涅耳积分研究了有限梁在加速载荷作用下的动态行为；LEE［18］基于拉格朗日方法分析了移动集中质量作用下Euler 梁的动力学行为，分析了质量与梁分离的可能性。

上述研究进展表明，关于轨道的动力响应研究已经取得不少成果，然而在变速移动荷载方面，参数讨论还不够丰富，内容还不够系统，亟待进一步地研讨。基于此，本文建立了变速移动荷载下城市轨道交通连续支承轨道梁模型，通过理论计算和数值分析对其振动规律进行了研究，结合广州轨道交通的具体项目讨论荷载参数（荷载移动初速度、加速度）以及轨道参数（轨道长度、弯曲刚度、支承刚度、支承阻尼）对轨道梁动力响应的影响。

1 运动控制方程及其求解

如图1 所示，简化轨道梁为连续支承Euler-Bernoulli简支梁，在其表面存在一个以速度v（t）沿着梁长方向移动的荷载F（x，t）。l为梁的长度（m）；EJ为抗弯刚度（N·m2）；m为单位长度质量（kg·m-1）；c为系统支承阻尼（kN·s·m-1）；κ为系统支承刚度（kN·mm-1）；ω（x，t）为梁的挠度（m）。于是由振动力学理可建立如下的运动控制方程：

图1 城市轨道交通连续支承轨道梁Fig.1 Continuously Supported Railway Beams for Urban Rail Transit

式中：F0为荷载恒值（kN）；δ（x）为Dirac 函数；xp（t）为荷载移动位置（m），xp（t）=v0t+at2/2，其中v0为荷载初速度（km·h-1）；a为加速度（km·h-1·s-1）。

根据振型叠加法，梁挠度ω（x，t）离散化为其振型函数yi（x）与广义坐标η i（t）的耦合，即

将式⑶代入式⑴中得

求解⑾式，可得求广义坐标η i（t），再代回式⑶最终可求出梁在移动荷载作用下的竖向振动位移ω（x，t）。

2 动力响应

为了更好地探究轨道梁的力学特性，本文基于广州轨道交通某项目，对不同基本参数引起梁的动力响应进行研究，轨道、荷载的基本参数及其数值或取值范围如表1 所示。结合上文理论公式，利用Matlab 软件对移动荷载作用下城市轨道交通连续支承轨道梁的动态响应进行数值分析与研究。

表1 轨道荷载基本参数Tab.1 Basic Parameters of Track Load

2.1 抗弯刚度的影响

不同抗弯刚度EJ下轨道梁挠度随时间的变化曲线如图2 所示，此时轨道梁长度l为50 m，移动荷载初速度v0=160 km/h，加速度a=3.6 km/（h·s），系统支承刚度κ=150 kN/m-1，系统支承阻尼c=100 kN·s/m。图2中从高至低3 条曲线的抗弯刚度分别为3.07×106N·m2、4.20×106N·m2、6.63×106N·m2，且曲线先增后减存在一个幅值。不同抗弯刚度对梁挠度幅值的影响如图3所示。曲线呈递减趋势，且由数值计算表明，当抗弯刚度从2×106N·m2增加到10×106N·m2时，梁的最大挠度约减少29%。即抗弯刚度的增加会减小梁的挠度，且效果明显。

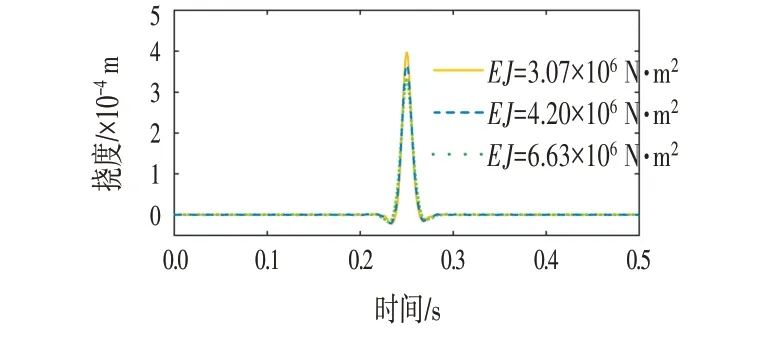
图2 不同抗弯刚度时梁挠度随时间的变化Fig.2 Changes of Beam Deflection with Time under Different Flexural Rigidity

图3 不同抗弯刚度对梁挠度幅值的影响Fig.3 Influence of Different Flexural Stiffness on Deflection Amplitude of Beam

2.2 支承刚度的影响

不同支承刚度κ下轨道梁挠度随时间的变化曲线如图4 所示，此时轨道梁长度l为50 m，移动荷载初速度v0=160 km/h，加速度a=3.6 km/（h·s），系统支承阻尼c=100 kN·s/m。图4 中从上往下3 条曲线的支承刚度分别为100 kN/mm、150 kN/mm、200 kN/mm，即随着支承刚度的增加梁的挠度逐渐减小。梁挠度幅值随着刚度变化的曲线如图5所示，当刚度从50 kN/mm 增加到100 kN/mm 时，轨道梁挠度幅值约下降了约57%；当刚度从100 kN/mm 增加到200 kN/mm 时，轨道梁挠度幅值下降了约19%，可见刚度对抑制振动起到了十分重要的作用。综上，梁挠度幅值与刚度呈负相关，且曲线斜率逐渐减小即刚度越大挠度幅值减小得越慢。

图4 不同支撑刚度时梁挠度随时间的变化Fig.4 Changes of Beam Deflection with Time under Different Support Stiffness

图5 不同支撑刚度对梁挠度幅值的影响Fig.5 Influence of Different Support Stiffness on Beam Deflection Amplitude

2.3 支承阻尼的影响

不同支承阻尼c下轨道梁挠度随时间的变化曲线如图6 所示，此时轨道梁长度l为50 m，移动荷载初速度v0=160 km/h，加速度a=3.6 km/（h·s），系统支承刚度κ=150 kN/m-1。图6 中从上至下3 条曲线的阻尼分别为100 kN·s/m、300 kN·s/m、400 kN·s/m，即梁的挠度随着阻尼的增加而递减，但值得注意的是这种递减很缓慢。梁挠度幅值随着阻尼变化曲线如图7所示，可以看到当阻尼从0 递增到400 kN·s/m 时，轨道梁挠度幅值仅减少了约4.8%。因此在实际应用中，阻尼的增加可以减少振动但效果有限。

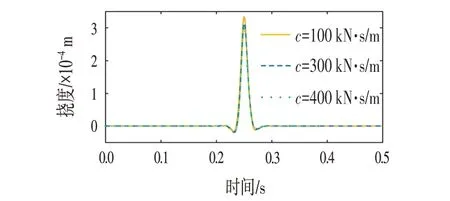
图6 不同阻尼时梁挠度随时间的变化Fig.6 Changes of Beam Deflection with Time under Different Damping

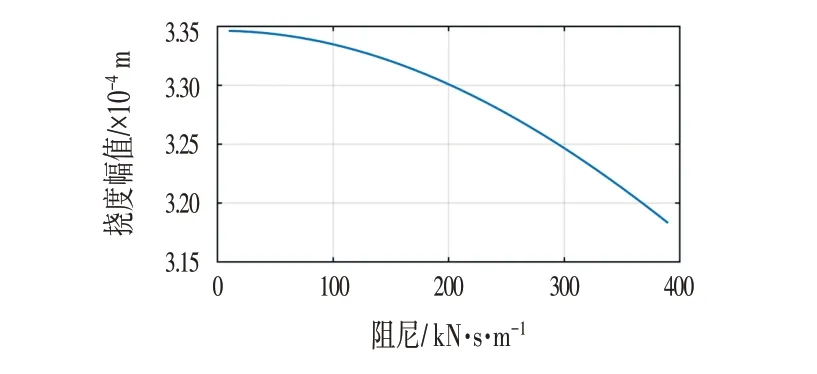
图7 不同阻尼对梁挠度幅值的影响Fig.7 Influence of Different Damping on Beam Deflection Amplitude

2.4 速度的影响

不同速度的移动载荷下轨道梁挠度随时间的变化曲线如图8所示，此时轨道梁长度l为50 m，移动荷载加速度v0=36 km/（h·s），系统支承刚度κ=150 kN/m-1，支承阻尼c=100 kN·s/m。图8 中从左至右3 条曲线分别代表荷载移动速度为120 km/h、72 km/h、36 km/h，当速度为36 km/h 时，挠曲线振幅最大且曲线突变的区域最广。图9研究了不同速度下轨道梁挠度最大值的变化规律，数值结果表明梁挠度最大值会随着速度递减，当速度从0增长到360 km/h时，挠度最大值增长率约为-0.15%。

2.5 加速度的影响

在支承刚度κ=150 kN/m-1，支承阻尼c=100 kN·s/m，移动荷载初速度v0=72 km/h 时，不同加速度下连续弹性支承有限长轨道梁挠度的变化曲线如图10 所示。图10 中从左至右曲线依次变宽即曲线突变的区域随着加速度的减小而变大。不同加速度下轨道梁挠度幅值的变化规律如图11所示，由图11可知，挠度幅值与加速度约成线性关系，且随着加速度递减。数值结果表明，当加速度从0 增长到360 km/（h·s）时，挠度幅值的增长率约为-0.08%。

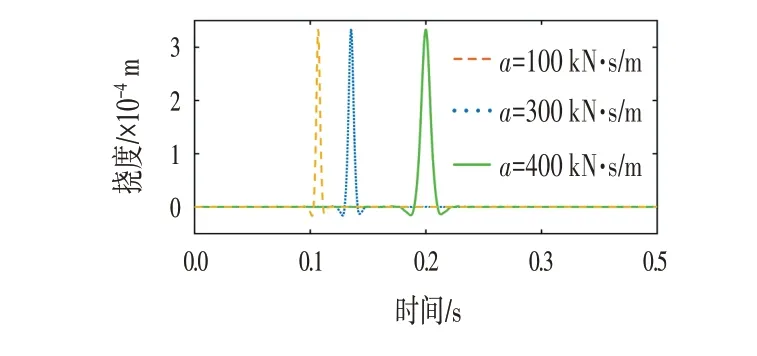
图10 不同加速度时梁挠度随时间的变化Fig.10 Changes of Beam Deflection with Time at Different Accelerations

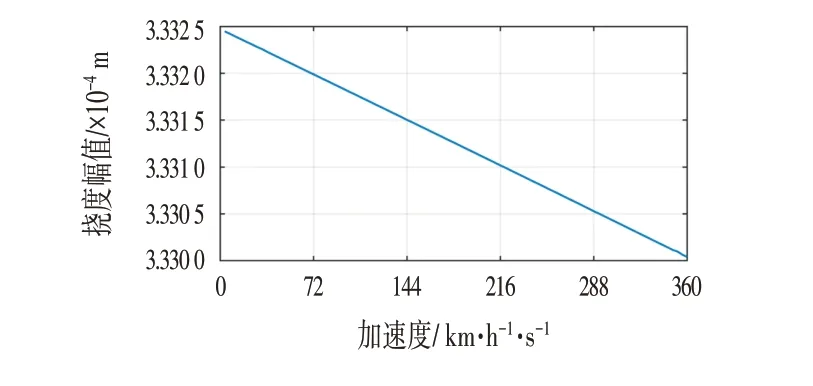
图11 不同加速度对梁挠度幅值的影响Fig.11 Influence of Different Accelerations on Beam Deflection Amplitude

3 结论

本文建立了移动荷载作用下连续支承轨道梁的理论模型，利用振型叠加法进行了理论推导得到了其运动方程的解析解，评估了各种参数对轨道梁动力响应的影响，得到了以下几个结论：

⑴连续支承有限长梁挠度随时间呈现先增后减的趋势，且存在着一个挠度最大值。

⑵轨道梁的抗弯刚度、支承刚度、支承阻尼的增加会使梁的挠度变小。其中抗弯刚度、支承刚度增加时梁挠度最大值减小的较快，即其对梁竖向振动的抑制效果最为明显。

⑶移动载荷初速度与加速度增加会减小梁的挠度，且值得注意的是，初速度和加速度会影响挠曲线突变区域的大小。即曲线会随着二者的增加而变窄，说明轨道梁对移动载荷的动力响应会变快。

综上所述，本文通过研究移动荷载作用下城市轨道交通连续支承轨道梁的振动响应，为车轨振动控制和城市轨道交通的抗振减振提供了参考，有一定的指导意义。