金属橡胶复合隔振器的动静态性能

任志英, 梁盛涛, 李金明, 白鸿柏, 赖福强

(福州大学机械工程及自动化学院, 金属橡胶与振动噪声研究所, 福建 福州 350108)

0 引言

航天飞行器受到强烈的随机振动激励, 导致仪器舱内电子精密仪器设备精度下降, 影响整体设备的工作性能, 针对仪器舱的减振至关重要. 早期对单机设备进行独立减振, 增加飞行器重量, 加大发射成本[1-3]. 因此, 提出整体减振方案, 将仪器设备等安装在板上, 采用减振器对集成结构进行整体减振和隔振[4-6]. 航天飞行器的工作环境较复杂, 要求减振结构能够承受高低温的影响. 金属橡胶因具有工作温度范围大、 抗腐蚀、 强度高等特性[7], 可在恶劣工程环境中应用. 它是一种由纯金属丝编织或缠绕而成的弹性多孔状材料, 其内部为螺旋状金属丝相互交错勾连形成的空间网状结构, 可实现压缩、 回弹及阻尼耗能等作用[8-9]. 它也是强非线性材料, 具有变刚度特性, 故金属橡胶减振器设计困难. 部分学者对金属橡胶与弹簧的组合展减振器用于空间飞行器仪器安装板的整体减振, 设计仪器安装板的地面振动实验并进行实验验证. 姜洪源等[10]研究金属橡胶与弹簧组合型隔振器的刚度和阻尼性能. 邹广平等[11]基于弹簧-金属橡胶组合减振器具有可设计刚度和较高承载能力的特点, 提出一种迟滞力学性能理论模型. 杨佩等[12]设计开发一款金属橡胶阻尼元件与线性弹簧并联减振器.

本研究设计一种对称式金属橡胶与线弹簧复合隔振器, 基于整体减振, 考虑安装板的柔性因素建立相应的等效线性动力学模型. 通过准静态力学试验, 分析线弹簧刚度、 金属橡胶密度和加载位移对复合隔振器准静态性能的影响. 进行随机振动试验, 研究复合隔振器在整体减振中的隔振性能.

1 整体隔振系统模型

1.1 隔振系统结构模型

隔振对象为某飞行器中仪器舱的安装板, 该安装板为一圆形铝合金薄板, 厚约6 mm, 直径430 mm. 仪器安装板总质量为12 kg, 整体隔振布置如图1所示. 共有6个周向均布的隔振器, 3个设备组件, 在安装板中心处沿两边等距分布. 被动隔振时, 通常需要对隔振系统进行解耦设计. 在工程上, 常用弹性中心法解耦, 其基本方式为, 当隔振系统的质心通过几个隔振器共同组成的弹性中心平面时, 隔振系统实现解耦.

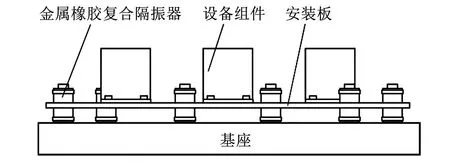
图1 整体隔振示意图Fig.1 Overall vibration isolation diagram

金属橡胶复合隔振器结构如图2所示. 该隔振器采用对称式分布, 将金属橡胶设计成空心圆柱形, 放置在线弹簧中间, 通过并联方式安装, 金属橡胶成型方向起到隔振作用. 由于采用对称分布, 所以上、 下两侧金属橡胶和线弹簧都一致. 钢套、 限位套筒和限位垫片的作用是将隔振器的振幅控制在设计范围内, 保护罩作用是防止金属橡胶在长时间工作时产生金属磨屑溢出, 从而导致电子设备短路等问题.

图2 金属橡胶复合隔振器结构Fig.2 Metal rubber composite isolator structure

1.2 隔振系统动力学模型

根据金属橡胶在成形方向上的力学特性, 同时基于整体隔振的结构模型, 将整体隔振系统简化为单自由系统, 如图3所示.

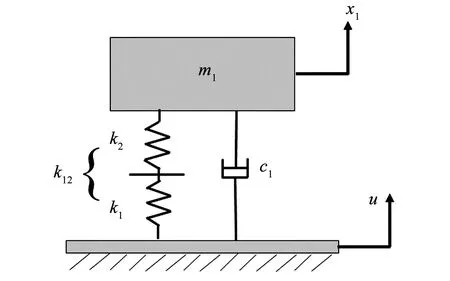
图3 金属橡胶复合隔振器整体隔振动力学模型 Fig.3 Metal-rubber composite vibration isolator overall vibration isolation dynamics model

根据图3的整体隔振系统力学模型, 可以得到动力学平衡方程. 即

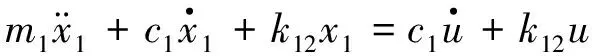
(1)

由于安装板与隔振器是串联关系, 故

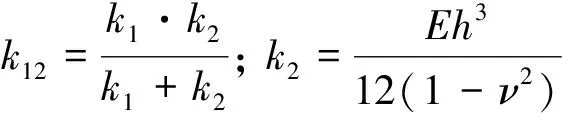
(2)

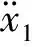
设质量块(m1)的瞬态响应(x1)和基础激励(u)为

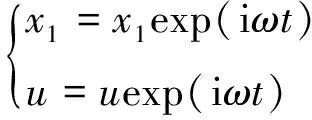
(3)

根据式(1)、 (2), 可推导得到整体隔振的加速度传递函数(Ψ). 即

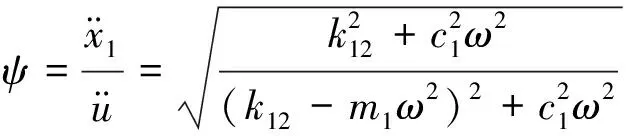
(4)

由随机振动理论可知, 通过基础随机激励功率谱密度(p1), 可计算出隔振后的响应加速度功率谱密度(p2). 即

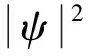
(5)

对p1和p2在频率范围内积分, 得出基座加速度激励的总均方根值(Erms)和响应加速度的总均方根值(Rrms), 计算出隔振效率(η). 即

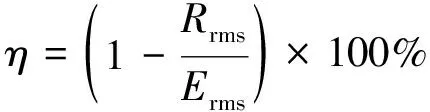
(6)

2 准静态力学性能试验

2.1 金属橡胶试件制备

制备所用金属丝为丝径0.15 mm的304不锈钢. 与金属橡胶复合的线弹簧刚度分别为15、 18、 35 N·mm-1. 空心圆柱形金属橡胶密度分别为2.0、 2.5、 3.0 g·cm-3, 如图4所示, 规格如表1所示.

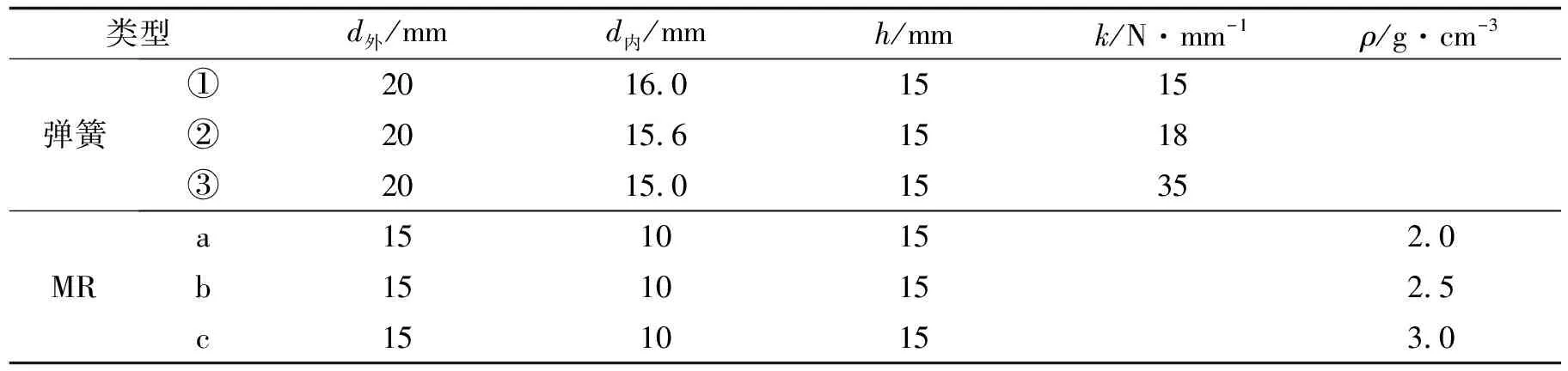
表1 线弹簧规格、金属橡胶规格

图4 空心圆柱形金属橡胶及复合形式Fig.4 Hollow cylindrical metal rubber and composite forms

2.2 静力学试验分析

金属橡胶复合样件的准静态试验, 如图5所示. 选用量程为1.0 kN的力传感器测量加卸载过程中的恢复力. 由于金属橡胶复合隔振器是对称式分布, 故只针对单侧的复合隔振器进行试验.

图5 电子万能材料试验机及实验工装Fig.5 Electronic universal materialtesting machine and experimental tooling

将单侧复合样件预压到安装高度, 然后对复合样件进行3～4次反复加卸载试验, 消除金属橡胶内部的残余应力. 取复合样件性能稳定后的第5次数据作为试验测量结果, 试验加载及卸载速度为0.5 mm·min-1. 本次试验研究线弹簧刚度、 金属橡胶密度和加载位移对复合样件准静态性能的影响.

2.2.1准静态性能表征参数

采用静态损耗因子(ηs)和静态割线刚度(ks)表征金属橡胶复合样件的静态阻尼特性和静态刚度特性. 由于该复合样件的线性刚度比较强, 非线性刚度比较弱, 故采用静态割线刚度表征. 即

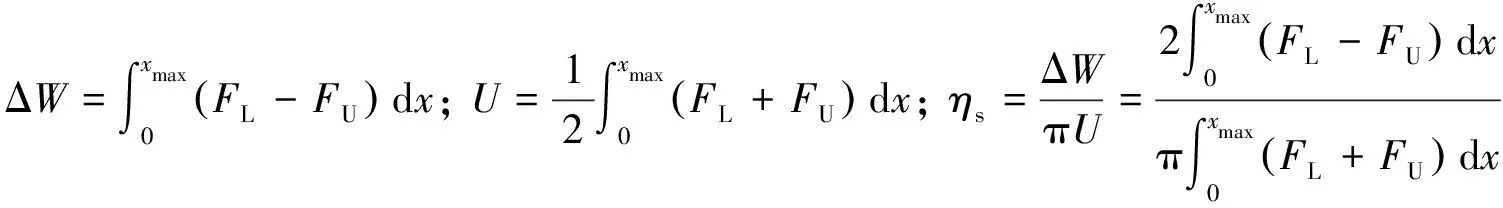
(7)

式中: ΔW为加载曲线与卸载曲线所包络的面积, 表示单个循环加载周期的能量损耗;FL为加载力;FU为卸载力;U为一个循环周期内储存的平均能量;xmax为最大位移.

金属橡胶材料宏观迟滞恢复力是由非线性弹性力和非线性阻尼力组成, 采用最大恢复力处的割线刚度来描述金属橡胶材料的承载能力, 为分析刚度特征, 同样采用割线刚度(ks)表征复合样件的刚度特性. 即

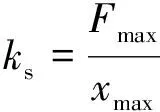
(8)

式中:Fmax为最大位移处的恢复力;xmax为最大位移.

2.2.2线弹簧刚度影响

研究3种刚度的线弹簧KB对复合样件静刚度与耗能特性的影响, 选取密度2.0 g·cm-3的金属橡胶进行试验, 且加载位移在预压的基础上为1.0 mm, 迟滞回线如图6所示, 静刚度和静态损耗因子如图7所示. 其中:x2为线弹簧位移,k3为线弹簧刚度.

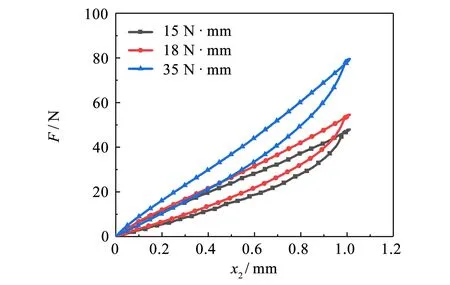
图6 线弹簧刚度迟滞回线 Fig.6 Hysteresis loop of wire spring stiffness

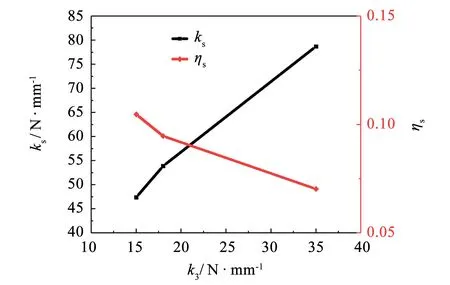
图7 线弹簧准静态性能Fig.7 Quasi static performance of wire spring

从图6可见, 加入线弹簧, 复合样件的加载曲线有较为明显的线性特征, 有轻微变刚度的特性. 从图7可知, 在相同密度的金属橡胶和加载位移下, 线弹簧刚度增加, 复合样件静刚度增大, 静态损耗因子减小. 故能量耗散系数与刚度成反比, 刚度的增加导致静态损耗因子的减小.

2.2.3金属橡胶密度影响

研究3种密度金属橡胶MR对复合样件静刚度与耗能特性的影响, 选取刚度为18 N·mm-1的线弹簧, 预压后加载位移为1.0 mm, 静态迟滞回线如图8所示. 静刚度和静态损耗因子如图9所示.

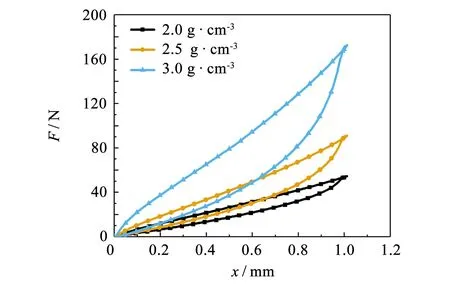
图8 金属橡胶迟滞回线Fig.8 Hysteresis loop of metal rubber

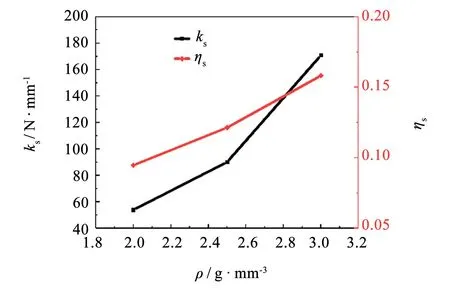
图9 金属橡胶准静态性能Fig.9 Quasi-static properties of metal rubber

从图8可见, 当金属橡胶的密度增大, 复合样件加载曲线的非线性增强, 逐渐恢复金属橡胶的3个变形阶段. 从图9可知, 加载位移一定, 复合样件静态刚度和静态损耗因子均随金属橡胶密度增大. 因为金属橡胶密度增大, 内部金属丝接触点增加, 从而增加干摩擦耗能.

2.2.4不同加载位移影响

将加载位移(d1)设为0.5 、 1.0 、 1.5 mm, 选取刚度为35 N·mm-1的线弹簧和密度为2.0 g·cm-3的金属橡胶进行试验, 静态迟滞回线如图10所示. 静刚度与耗能特性的变化, 如图11所示.

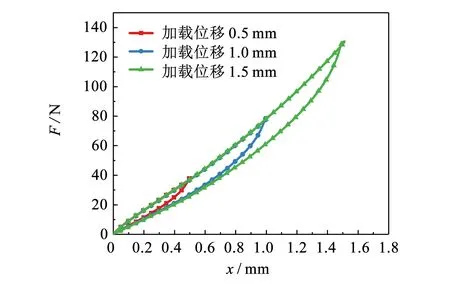
图10 复合样件迟滞回线Fig.10 Hysteresis loop of composite sample

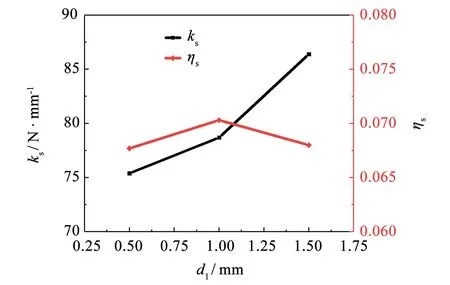
图11 复合样件准静态性能Fig.11 Quasi static performance of composite sample

从图11可见, 复合样件随加载位移增加, 静态刚度缓慢的增大一定程度后增大明显, 这是因为当金属橡胶压缩率超过一定程度时, 刚度会发生指数型增大. 然而, 随着加载位移的增加, 复合样件的静态损耗因子有先增大后减小的趋势, 但变化趋势对于线弹簧刚度的影响较小.

3 随机振动试验

3.1 试验装置

随机振动试验台如图12所示, 包括DC-4000-40型电动振动台台体、 SCU-200型系统控制器、 FJ-3000型风机、 SA-40型功率放大器、 RC-3000型振动控制仪、 GX20100型空气压缩机、 电脑、 7071型加速度传感器和金属橡胶复合隔振器. 工作原理如图13所示. 布置4个加速度传感器, 采用双通道输入控制. 控制点1和2安装在基座上, 输入激励为两点的加权平均. 监测点3和4安装在设备组件上, 如图14所示.

图12 振动台及试验工装Fig.12 Shaking table and test tooling

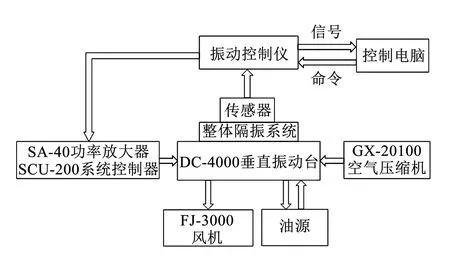
图13 振动台工作原理图Fig.13 Working principle of shaking table

图14 测点分布Fig.14 Distribution of measuring points

3.2 加载条件

采用随机振动谱型如图15所示. 随机振动谱的加速度总均方根值Grms=13.84g, 全量级激励时间为5 min, 随机谱下的采样频率为5 Hz, 加载方向为轴向, 加速度传感器控制点布置在基座上对称安装, 其中p代表功率谱密度.

图15 随机振动试验振动谱型Fig.15 Vibration pattern of random vibration test

3.3 随机响应分析

根据上节复合样件静态实验得到的结果, 进行随机振动实验. 实验涉及5种金属橡胶复合隔振器的类型如表2所示.

表2 复合隔振器类型

进一步分析隔振性能, 进行线弹簧隔振器和金属橡胶复合隔振器整体隔振的振动试验. 本次试验测试3种线弹簧隔振器、 5种类型复合隔振器整体隔振的效果. 各隔振类型测点响应结果如表3所示.

表3 各测点均方根值及系统一阶固有频率

边缘设备组件上的测点3结果最佳, 选该测点进行隔振效率计算. 从表3可见, 系统一阶固有频率增加, 系统整体隔振效率减小. 从隔振器类型的响应结果可知, 在中间部分组件设备的隔振效果比边缘部分低, 响应均方根值更大, 如监测点3和4, 故在仪器设备安装时, 尽量布置在靠近安装板的边缘.

金属橡胶密度不变, 系统的一阶固有频率随着线弹簧刚度增大而增大, 隔振效率逐渐减小. 线弹簧刚度不变, 系统隔振效率随金属橡胶密度的增大而减小. 故要获得较好的隔振效果, 金属橡胶的密度不宜过大. 因此在进行随机振动实验前, 进行金属橡胶复合减振器的准静态性能实验, 挑选出隔振性能更优的隔振器. 各隔振器类型在响应监测点 3中谐振点处的响应峰值(p3)和放大倍数(β)如表4所示. 并选取3种系统固有频率水平下线弹簧隔振器与金属橡胶复合隔振器的响应曲线进行对比, 如图16所示.

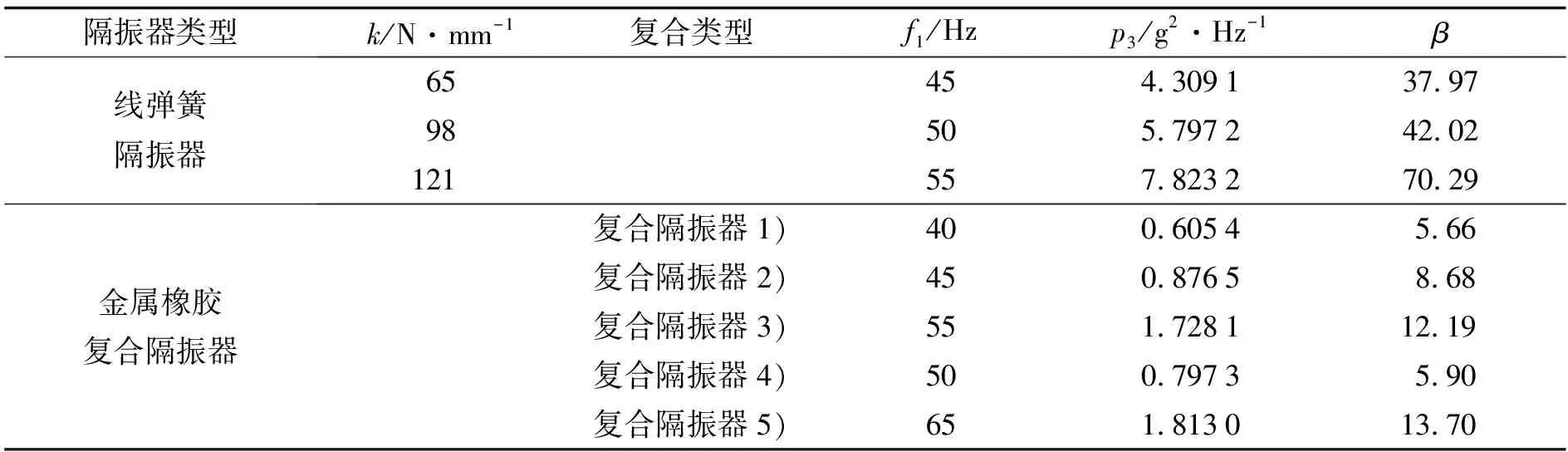
表4 响应监测点3中谐振点处峰值和放大倍数

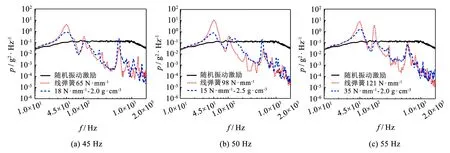
图16 相同一阶固有频率水平下响应结果对比Fig.16 Comparison of response results at the same first-order natural frequency level

对比放大倍数可知, 固有频率相同时, 复合隔振器在谐振点处的峰值衰减是线弹簧隔振器的5倍以上; 谐振频率越小, 峰值衰减越快. 将横纵坐标取对数, 得到伯德图16. 可知系统随机振动响应在频段120 Hz以后都有较大程度衰减, 在第1个谐振点处有放大效果, 金属橡胶复合隔振器相比线弹簧隔振器都在一定程度上有所衰减.

4 结语

设计一种对称式金属橡胶与线弹簧复合的隔振器, 基于整体隔振, 考虑安装板的柔性因素建立相应的等效线性动力学模型. 进行动静态力学试验, 采用静态损耗因子(ηs)和静态割线刚度(ks)表征金属橡胶复合样件的准静态性能, 并得出以下结论.

1) 当金属橡胶的密度增大到一定程度后, 复合样件加载曲线的非线性开始增强, 逐渐恢复金属橡胶材料所具有的3个变形阶段.

2) 静态损耗因子随着线弹簧刚度的增大而减小, 随着金属橡胶密度的增大而增大. 加载位移的不断增加, 复合样件的静态损耗因子有先变增大后减小的趋势, 但变化趋势对于线弹簧刚度的影响较小.

3) 装有金属橡胶复合隔振器的整体隔振系统在谐振点处的峰值衰减是线弹簧隔振器的5倍以上, 系统的随机振动响应在频段120 Hz之后均有较大程度衰减, 隔振效率达到60.6%. 对于线弹簧隔振器, 谐振点处峰值放大倍数降到5倍左右, 基本符合隔振设计要求.