丙酮-丁酮醇、 丙酮-二丙酮醇二元汽液相平衡

李胜男, 王清莲, 张鹏, 何剑洋, 黄智贤

(1. 福州大学石油化工学院, 福建 福州 350108; 2. 厦门金达威股份有限公司, 福建 厦门 361022)

0 引言

丁酮醇(别名: 4-羟基-2-丁酮)是一种广泛应用于合成维生素A和香料的中间体, 在制药和食品加工行业具有极广阔的应用前景[1]. 一般而言, 丁酮醇的生产途径主要有2条, 一条是由甲醛和丙酮羟醛缩合生成丁酮醇, 另一条是由1, 3-丁二醇选择性氧化生成丁酮醇[2]. 其中, 甲醛和丙酮羟醛缩合反应由于原料甲醛和丙酮廉价易得, 而成为目前最常用的丁酮醇合成方法[3]. 但是, 在羟醛缩合反应过程中, 丙酮也会发生自缩合反应生成副产物二丙酮醇, 使缩合反应液组分复杂[4-5]. 后续为了得到丁酮醇产品, 还需要借助精馏进行分离纯化[6].

在精馏设计中, 待分离组分间的汽液相平衡数据是必不可少的基础数据, 但目前有关丙酮-丁酮醇、 丙酮-二丙酮醇二元体系的汽液相平衡研究未见文献报道. 因此, 本研究测定101.3 kPa下二元体系汽液相平衡数据, 并采用Wilson、 NRTL和UNIQUAC模型对实验数据进行关联, 获得相应的二元交互参数.

1 实验步骤与方法

1.1 试剂及仪器

丁酮醇(质量分数为95%, 分析纯)和二丙酮醇(质量分数为99%, 分析纯)从阿拉丁试剂网采购, 丙酮(质量分数为99%, 分析纯)购自国药试剂网. 丁酮醇试剂采用精密精馏进一步提纯. 气相色谱分析结果表明, 丁酮醇、 二丙酮醇和丙酮纯度均超过99%. 采用改进的Rose汽液平衡釜, 实验装置如图1所示. 外层设有真空保温套. 加热量由变压器调节, 确保釜内的沸腾循环. 汽液平衡温度采用水银精密温度计测量, 精度0.01 K.

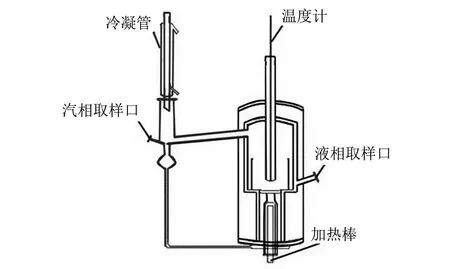
图1 Rose汽液平衡釜Fig.1 Rose vapor liquid equilibrium kettle

1.2 实验步骤

1) 配置一定量不同浓度的丙酮-丁酮醇/丙酮-二丙酮醇混合溶液, 从液相取样口加入混合溶液, 直至液面处于液相取样口上下端之间.

2) 打开冷凝水和加热电源, 调节加热功率使釜内液体沸腾(气泡逐个冒出, 不成股).

3) 当水银温度计读数保持恒定且能维持60 min, 则认为此时釜内汽液相达到平衡. 读取空盒气压表上的大气压力、 室内温度和精密温度计上的温度并记录. 分别从汽相和液相取样口取样, 使用气相色谱仪进行定量分析. 每个样品至少分析3次.

4) 重复实验, 得到丙酮-丁酮醇、 丙酮-二丙酮醇的汽液相平衡数据, 绘制汽液相平衡图.

1.3 气相色谱测定分析条件

汽液相组成采用岛津气相色谱GC-2014C分析, 色谱柱选用SH-Rtx-5(30 m × 0.25 mm × 0.25 μm). 以乙酸乙酯为内标物定量分析. 色谱分析条件为: 进样温度设置为443 K, FID检测器温度设置503 K. 采用程序升温法, 初始柱温313 K, 停留2 min, 以40 K·min-1的速率升温至363 K. 接着, 以10 K·min-1的速率升温至383 K, 停留2 min. 而后, 以25 K·min-1的速率升温至423 K, 停留2 min. 最后, 以40 K·min-1的速率升温至453 K, 停留2 min.

1.4 温度校正方法

尽管实验要测量101.3 kPa下的汽液相平衡数据, 但是实验过程中室内压力不一定为该压力, 且室内温度会在一定程度上影响测量值, 所以需要进行压力与温度的校正, 进而得到 101.3 kPa下的平衡温度.

在校正温度前, 需要先校正空盒气压表测得的压力(P), 即

P=Ps+ΔPt+ΔPs+ΔPd

(1)

式中:Ps为空盒压力表上的压力, kPa; ΔPt为温度校正, kPa, ΔPt=-0.006t;t为空盒压力表上的示数, ℃; ΔPs为示数校正, 实验所处大气压下ΔPs=0; ΔPd为普通校正, 值为-0.12 kPa.

压力校正后, 再进行平衡温度(T)校正. 即

(2)

式中:Texp为平衡温度, K;Bi、Ci为组分i的Antoine常数;xi为平衡时液相组成.

2 实验结果与讨论

2.1 汽液相平衡数据

在101.3 kPa压力下, 丙酮-丁酮醇、 丙酮-二丙酮醇的汽液相平衡数据见表1和表2.

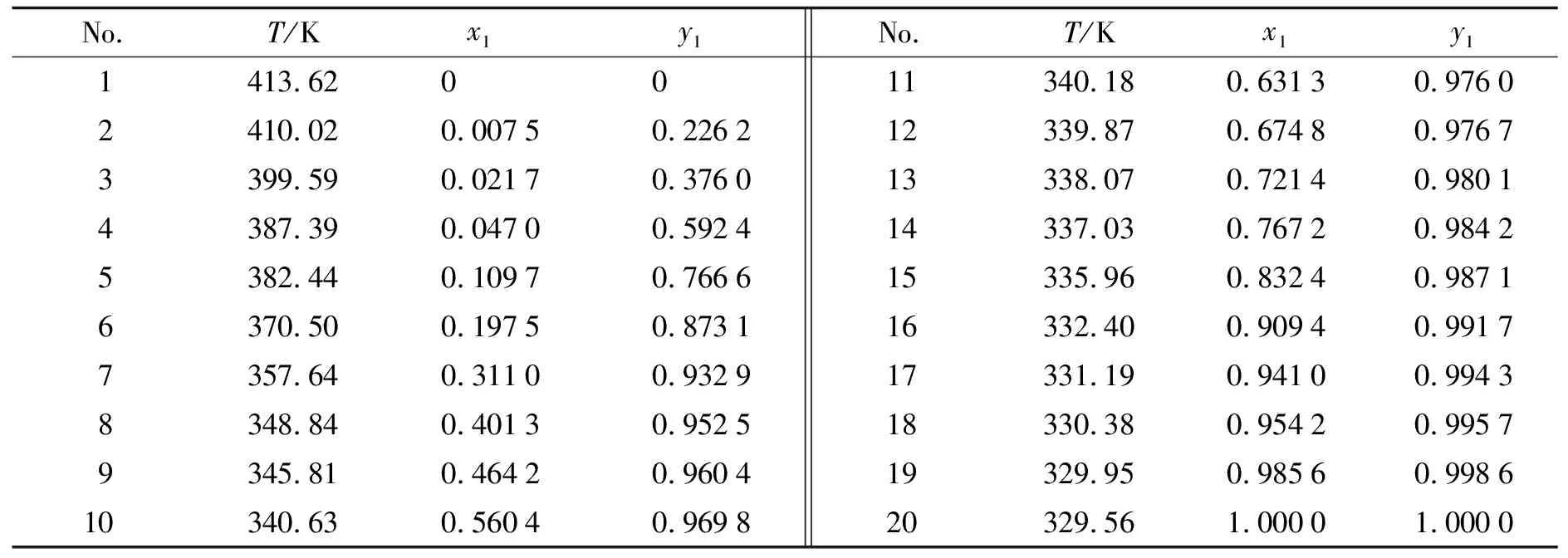
表1 101.3 kPa下丙酮-丁酮醇汽液相平衡实验数据

表2 101.3 kPa下丙酮-二丙酮醇汽液相平衡实验数据

2.2 汽液相平衡模型

常压下, 汽相为理想气体, 液相为非理想溶液, 汽液相平衡公式[7]可以简化为

(3)

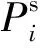
体系内各物质的Antoine方程、 van der Waals参数ri和qi如表3所示.

2.3 模型参数回归

目前, 混合溶液的活度系数关联式大多是通过一定的假设来进行简化, 在一定理论基础上得到的半经验半实践模型. 其中, Wilson、 NRTL和UNIQUAC模型是最为常用的3种模型. 故选用这3种模型对汽液相平衡数据进行关联.

1) Wilson模型.

Wilson活度系数方程[9]为

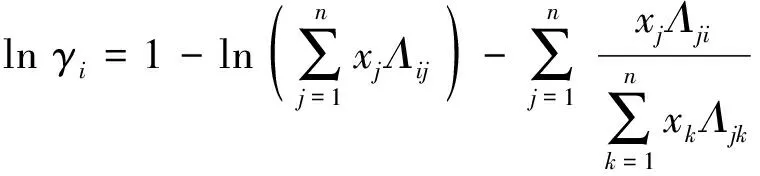
(4)

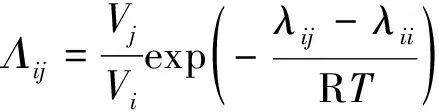
(5)

式中:Λij为Wilson模型参数,Λij≠Λji,Λii=Λjj;Vi和Vj分别为i和j纯组分摩尔体积, m3·mol-1; (λij-λii)为二元交互参数,λii=λjj.

2) NRTL模型.

NRTL活度系数方程[10]为

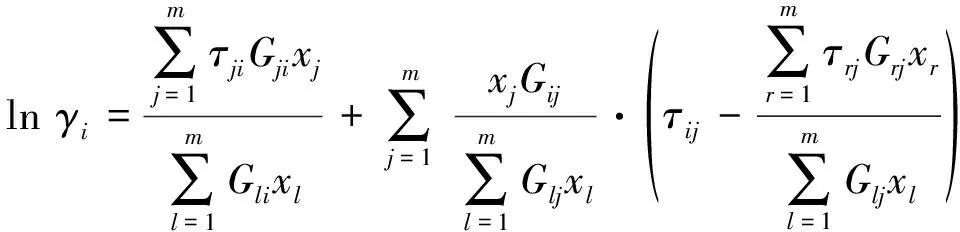
(6)

式中:τji和Gji为NRTL模型参数, 是非随机参数,τji=(gji-gii)/(RT),gji为组分j和组分i之间的交互作用能量参数, 且gji=gij;Gji=exp(-αjiτji),αij为混合物非自由度相关的可调特性参数,αij=αji.

3) UNIQUAC模型.

UNIQUAC活度系数方程[11]为

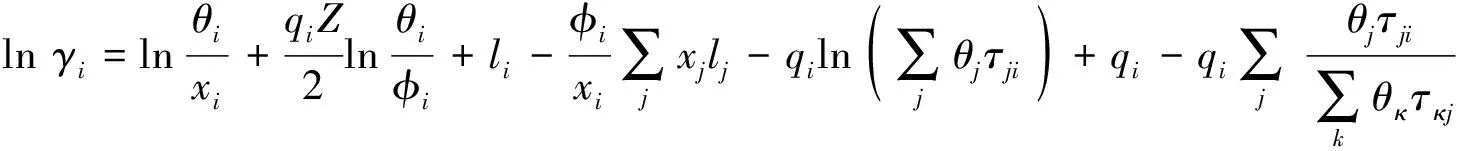
(7)

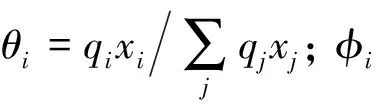
依据给定的汽液相平衡数据, 由Wilson、 NRTL和UNIQUAC模型关联后得到各自对应体系的汽相组成, 结果如表4和表5所示.

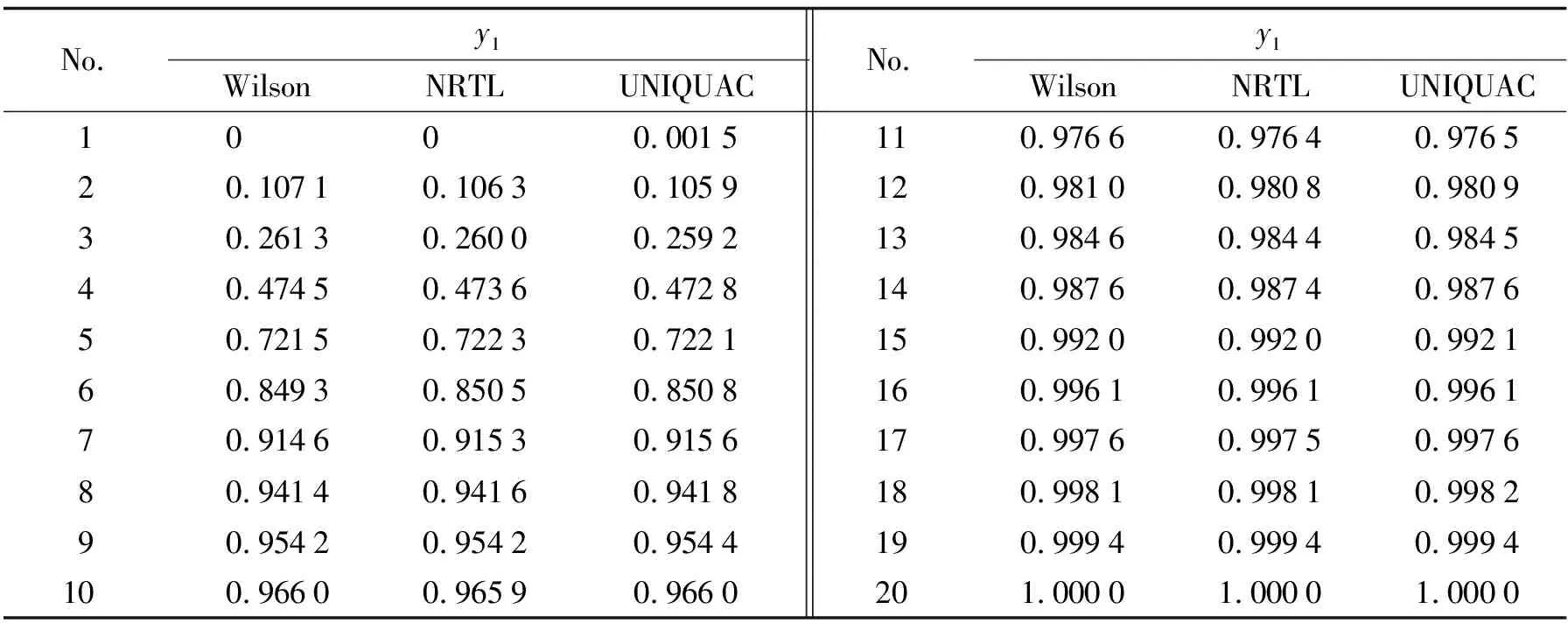
表4 101.3 kPa下丙酮-丁酮醇二元体系的汽相组成计算值

表5 101.3 kPa下丙酮-二丙酮醇二元体系的汽相组成计算值

丙酮-丁酮醇、 丙酮-二丙酮醇二元体系与3种活度系数模型关联后得到的T-x1-y1见图2和图3.其中:x1表示丙酮液相摩尔分数;y1表示丙酮汽相摩尔分数.

图2 丙酮-丁酮醇的T-x1-y1图Fig.2 T-x1-y1 diagram of acetone-butanone alcohol

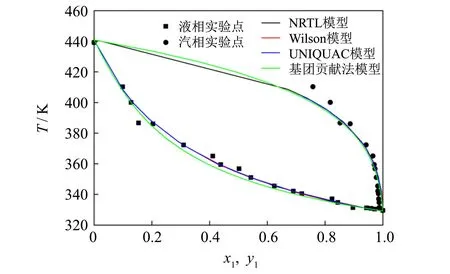
图3 丙酮-二丙酮醇的T-x1-y1图Fig.3 T-x1-y1 diagram of acetone-diacetone alcohol

从图2和图3可以看出, 对于丙酮-丁酮醇和丙酮-二丙酮醇2个二元体系, Wilson、 NRTL和UNIQUAC 3个模型预测的汽液相平衡数据几乎重叠在一起. 因此, 选用这3个模型对实验数据进行预测是合理的[12]. 而对于物性数据缺失的体系, 常常采用基团贡献法进行估算[13]. 从图2可见, 采用基团贡献法预测的丙酮-丁酮醇汽液相平衡数据与实验测量数据偏差很大, 而从图3可见, 丙酮-二丙酮醇汽液相平数据与实验数据相对较为接近.

选用均方根偏差(R)表示3种模型的拟合偏差, 即

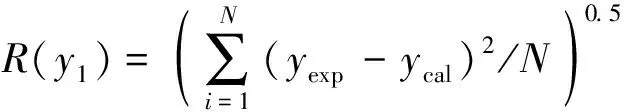
(8)

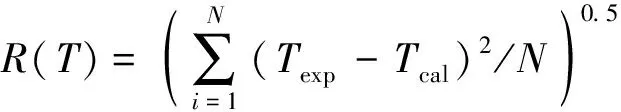
(9)

对上文二元体系汽液相平衡数据进行拟合, 估算模型二元交互参数. 以上结果均列于表6.

表6 二元体系模型参数及其均方根偏差

以汽相组成偏差的平方和为目标函数, 检验估算的二元交互参数的准确性[14], 即

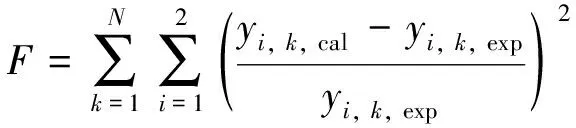
(10)

表6中3个模型的汽相均方根偏差都小于5%, 说明3个模型都能准确描述二元体系的汽液相平衡行为, 且3个模型的关联精度相当.

a表示Wilson模型的参数一是λij-λii, NRTL模型的参数一是gji-gii, UNIQUAC模型的参数一是uij;

b表示Wilson模型的参数二是λji-λjj, NRTL模型的参数二是gij-gjj, UNIQUAC模型的参数二是uji.

2.4 热力学一致性校验

汽液相平衡实验数据是否可靠, 可以采用面校验法对丙酮-丁酮醇、 丙酮-二丙酮醇二元体系汽液相平衡数据进行校验[15]. 选择Herington法对实验数据进行热力学一致性校验, 即

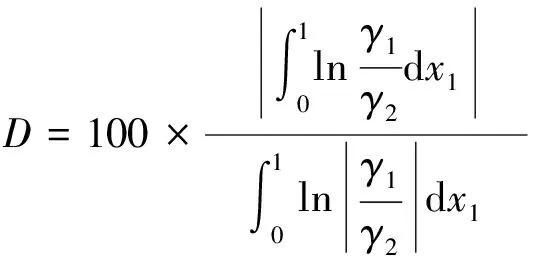
(11)

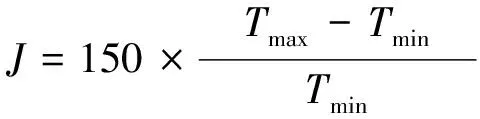
(12)

式中:D为定义偏差;J为压力熵.根据计算出的数据绘图并计算出D和J.若D-J<10或D

以ln(γ1/γ2)为纵坐标,x1为横坐标做图, 以横轴为分界线, 计算在0～1区域围成的面积, 结果如图4所示, 计算得到的D和J等数据如表7所示.

表7 汽液相平衡数据的热力学一致性检验结果

图4 二元体系的ln(γ1/γ2)-x1曲线Fig.4 ln(γ1/γ2)-x1 curve of binary system

从表中数据可见, 采用Herington法计算得到的D小于J, 且D-J<10, 这表明测得的丙酮-丁酮醇和丙酮-二丙酮醇的汽液相平衡数据符合热力学一致性的要求, 数据可靠[16].

3 结语

采用Rose汽液相平衡釜测定101.3 kPa下丙酮-丁酮醇和丙酮-二丙酮醇二元体系的汽液相平衡数据, 并用Wilson、 NRTL、 UNIQUAC模型对实验数据进行关联, 得到相应的二元交互参数. 利用二元交互作用参数进行预测, 绘制了实验值与模型预测值的T-x-y相图, 并计算得到2个二元体系的均方根偏差. 以上数据均表明, 实验值与模拟值拟合良好. 采用Herington半经验法对实验数据进行热力学一致性检验, 发现所有的数据均可通过热力学一致性检验, 3个模型均能准确描述二元体系的汽液相平衡行为.