海床破坏下的海底管道路由区水动力冲淤特性研究与应用
2024-03-06淳明浩于德周杨肖迪罗小桥姚志广
淳明浩,于德周,杨肖迪,罗小桥,姚志广,徐 爽
1.中国石油集团工程技术研究有限公司,天津 300451
2.中国石油集团海洋工程重点实验室,天津 300451
3.中国石油集团海洋工程(青岛)有限公司,山东青岛 266520
海底管道作为海底油气资源集输的重要枢纽,其安全运维是海上油气资源开发中的关键环节之一[1-4]。海底管道路由区在未受到外来破坏之前,通常会处于一种相对的海床冲淤平衡状态[5-7]。然而,由于管道所处路由区的水动力条件变化、人为作业活动或自然因素破坏导致的周边海洋环境条件改变,造成原有冲淤平衡状态的破坏[5-6],均可能引起海底管道路由区局部或整体的冲刷侵蚀[3-4],导致海底管道上覆土体保护层减薄和侵蚀[4-6],威胁海底管道安全。
管道路由区海床的稳定是海底管道安全与稳定的有力保障,诸多海底管道安全风险常由海床的冲淤变化引起[5-7]。目前,针对海底管道及其路由区的研究多集中于管道本体、路由区选址等方面,对于管道路由区海床冲淤侵蚀的研究较少[1-6]。
同时,海底管道路由区冲淤测量与分析的方法主要来源于设备观测、原型测量分析、物理模型及数值模型模拟等手段[8-11]。本文通过研究,提出基于海底管道路由区水动力冲淤特征的分析方法,对于明确水动力条件变化对管道路由区的影响可以起到支撑与促进作用,可与海底管道路由区的观测调查形成综合互补的路由区风险分析评估技术,有助于提高海底管道路由区相关风险的分析评估效率和管道运维保护的科学性。
1 研究区域概况
某海底管道位于广东省深圳市境内珠江口海域,起点为深圳大铲岛,终点为深港边界,管道途经采砂区、铜鼓航道、矾石浅滩区、临近锚地等特殊地段,海底段全长14.78 km[1-2](以起点为KP 0、终点为KP 14.78表示)。2018年12月探测调查发现,管道路由区受到海底采砂作业破坏,形成巨大采空区,对原有水动力冲淤平衡造成了破坏[2]。为研究海底管道路由区当前水动力冲淤特性,在路由区与采砂区勘测详查的基础上,2019年进一步开展了水动力参数观测、表层沉积物取样与组成测试,根据获得的水动力参数和沉积物组成参数,研究建立水动力冲淤数值模拟模型,评价海底管道路由区的冲刷侵蚀趋势,为管道运行维护和风险评估提供支持。海底管道地理位置[1]如图1所示,水动力参数观测与沉积物取样位置分布[2]如图2所示。
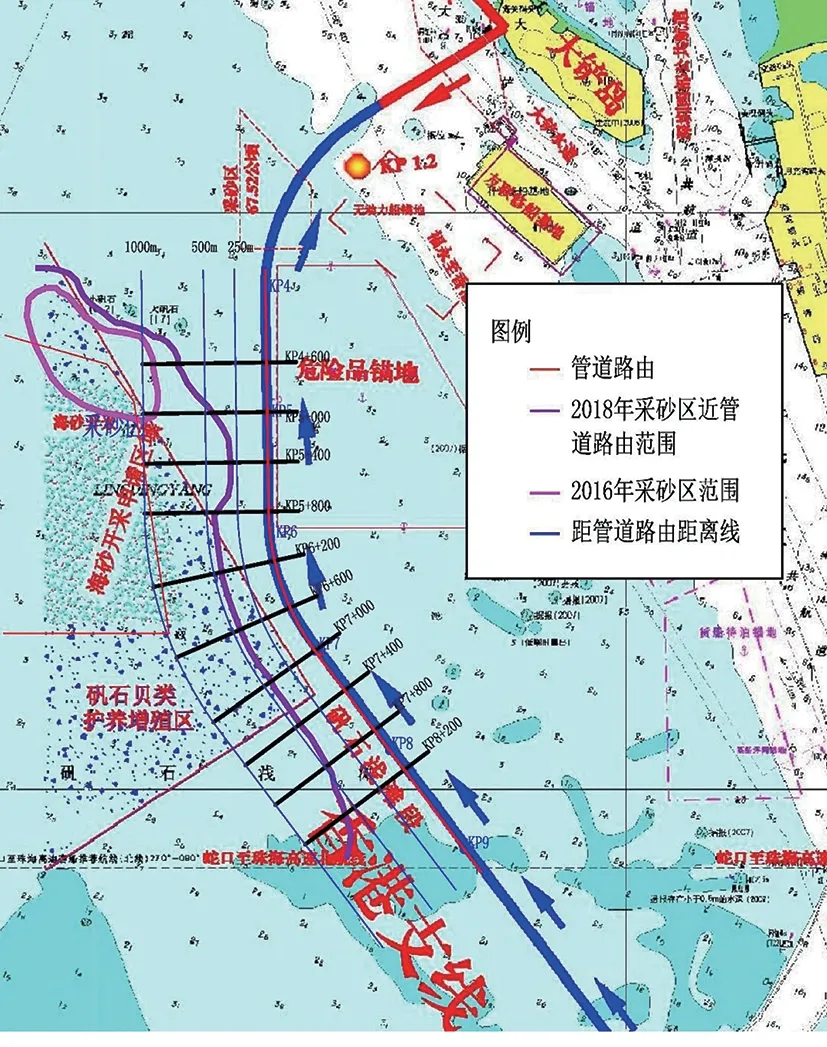
图1 海底管道地理位置

图2 水动力参数观测与海底沉积物取样位置分布示意
2 水动力冲淤特性方法构建
2.1 原理与技术路线
本文所研究管道路由区海床由于采砂破坏而形成了巨大凹坑,因而其原水动力冲淤平衡已破坏,当前水体的紊流状态对海床冲淤变化影响最大[7-8],因此采用紊流模型进行冲淤分析。
在水动力模拟分析中,当采用紊流模型模拟流场时,可获得任意水质点的流速,计算海床泥沙受到的剪切力,再根据土质的泥沙起动剪切力,判断海床表面的泥沙是否运移起动[12]。模拟分析过程中,通常将运动的泥沙分为悬移质和推移质,由海床表面的剪切力和推移质输运公式得到推移质的输沙率,通过求解悬移质质量浓度控制方程得到分析区域的泥沙质量浓度,进而计算悬移质的输沙率,总的输沙率为推移质输沙率和悬移质输沙率之和[8-9]。在包括海床面的封闭空间内,利用质量守恒原理求得海床面的变化,经过多次的迭代,得到海床稳定后的形态[14-15]。针对本研究区域的管道路由区水动力冲淤模拟,共建立了流场模型、泥沙输运模型及地形变化模型三种模型[10-12]。本次水动力冲淤模拟模型的基本逻辑关系如图3所示。

图3 海底水动力冲淤模型逻辑关系
2.2 数值模型研究
根据上述确定的紊流水动力冲淤模型,确定本次水动力冲淤模型的各个方程组成。
其中,模拟管道路由区的流场模型由时均雷诺方程和连续方程组成[7-9]。在笛卡尔坐标系下的无因次时均雷诺方程如下[14-17]:
式中:t为时间,s;x、y、z是笛卡尔坐标系坐标,m;η为水面标高,m;p为水体压强,Pa;u、v、w分别对应x、y、z坐标方向上的水体速度分量,m/s;Re为雷诺系数;τ11为xx平面的剪切应力,Pa;τ12为xy平面的剪切应力,Pa;τ22为yy平面的剪切应力,Pa。
无因次时均连续方程[14-17]如下:
由于以上基本方程构成的方程组并不封闭,本次数值模拟采用标准k-ε紊流方程进行封闭。标准k-ε紊流方程[14-17]如下:

表1 标准k-ε紊流模型的参数取值
表1 中的Cμ、σk、σε、Cε1、Cε2均为紊流模型经验常数。
2.3 泥沙输运模型研究
泥沙运动方式通常分为悬移质移动和推移质移动两种[14,15,19]。在水动力模拟分析中,运动状态泥沙中的推移质为紧贴底面很薄的一层泥沙颗粒,其在运动中不离开海床底面,而悬移质会因对流和扩散而分布到整个流场中[17-19]。根据2019 年在如图2所示的管道路由区进行的海底沉积物取样成分分析报告,本研究区的沉积物组成类型为以淤泥质砂质黏土和砂质黏土为主,还有较少粉砂,故本次研究中对于泥沙运动同时考虑泥沙悬移质和推移质的运动。
2.3.1 悬移质输运模型分析
本研究区悬移质的输运受泥沙浓度控制[20-22]。本次模拟模型采用对流扩散方程来求解泥沙质量浓度,对流扩散方程表示如下[7-9,20]:
式中:c为泥沙的质量浓度,g/m3;ωs为泥沙颗粒在水中的沉降速度,m/s;σc为紊流Schmidt数,表示泥沙扩散系数与涡黏系数的关系[19-20],本研究中σc=1.0。
海床附近的泥沙质量浓度求解公式[7-9,20]如下:
式中:d50为静水深度,m。Δb为海床的参考高度,即海床到悬移质输沙的距离,m。u*为泥沙摩阻速度,N·s/m2;u*cr为泥沙的临界摩阻速度,N·s/m2。D*为水体黏滞系数[20-21]。
本次模拟模型的泥沙质量浓度在海底的边界条件设定为:当T>0时,利用式(7)计算海底边界的泥沙质量浓度;当T≤0时,海底泥沙的质量浓度在边界法线方向梯度为0。在运动水体的圆柱表面和自由面,水体边界法线方向的泥沙流量为0,泥沙质量浓度计算方程[7-9,20]如下:
式中:β为水体边界与垂线之间的夹角,(°);n为水体边界法线方向的单位向量[22]。
求解方程(8),得到分析区域任一点的泥沙质量浓度,结合流场分析结果,悬移质输沙率qs的计算公式[7-9,20]如下:
式中:yb为海床的垂直坐标,m;H为b点的水体深度,m。
2.3.2 推移质输运模型分析
本研究区推移质的输运受泥沙密度、流体密度及流体速度控制[20-22],本次数值模拟中推移质输沙率[23-26]的计算公式[7-9,20]如下:
式中:qb为单位宽度内的体积输沙率,kg/s;g为重力加速度,m/s2;s=ρs/ρ,为泥沙密度和流体密度的比值。
2.4 地形变化模型设定
本研究区的海底地形变化模型的建立依据为泥沙在海床区域的质量守恒原则[25-28],因此本次模型对于地形变化引起的海床变化采用的控制方程[7-9,20,29]如下:
式中:po为泥沙孔隙率,%;qT为总泥沙输运率,kg/s,等于推移质输沙率qb和悬移质输沙率qs之和[18-22]。
3 数值模型分析计算
由于管道路由区受到人为作业的破坏,形成了海底采砂坑,造成管道路由区域海床形态的巨大变化,这种地形变化对管道路由区的水动力特征产生了影响,导致路由区不同区域的泥沙冲刷侵蚀状况的改变。为深入分析这种冲淤变化及其影响,采用不同模型尺度进行数值模拟计算。
为了提高数值模拟计算的准确度以及更好地模拟分析不同尺度下的路由区冲淤特性,对整个研究区设置了大区域模型和小区域模型。其中,大区域模型以涵盖管道路由区、外部海域为基础,主要模拟珠江口外部的海洋水动力对路由区的影响。小区域模型以管道路由区、周围径流区及潮流区为基础,主要模拟潮流和径流水动力对路由区的影响。
3.1 大区域模型设置
本次水动力冲淤模拟的大区域模型的计算范围为针对海底管道所处的广东省深圳市珠江口外的近岸海域,计算区域范围为12.7°N~29.4°N、105.6°E~124.5°E,并对工程模型区域网格进行加密。该模型的网格布置与地形分布如图4所示。
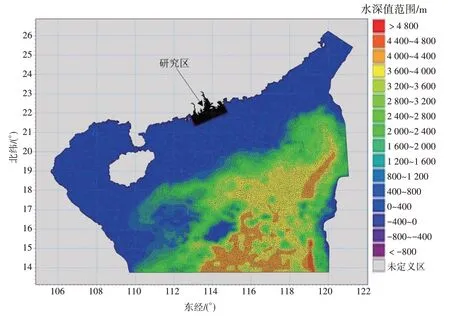
图4 大区域模型计算范围与网格划分图(黑色区域为研究区)
3.2 小区域模型设置
本次水动力冲淤模拟的小区域模型的计算范围为海底管道路由区临近的珠江口伶仃洋和外部海域。本研究中,小区域模型采用三维垂向平均模式。为了更好拟合水-陆边界,模型利用非结构三角网格技术对计算区域进行空间剖分。此类型三角网格设计灵活,便于调整网格疏密,有助于减少锯齿状岸线对模拟计算结果的不利影响。小区域模型计算范围与地形分布如图5所示。
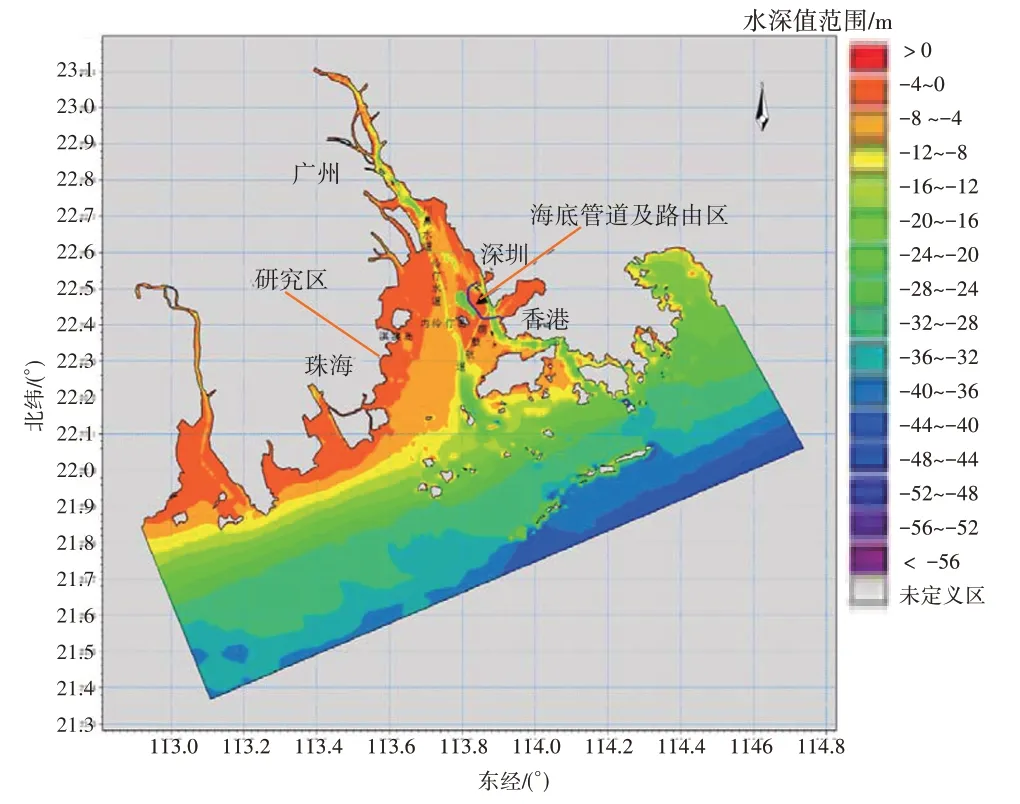
图5 小区域模型计算范围与水深地形分布图(图中黑线为管道位置)
3.3 边界条件设置
由于管道路由区域受到外海来水、内陆来水、海底沉积物等多重影响,因此采用多重边界条件对模型进行限定,包括开边界条件、闭边界条件、表面边界条件、底部边界条件、干-湿边界条件。
3.3.1 开边界条件
本次模拟模型的开边界条件为水域边界条件,即管道路由区所处的珠江口水域。在此边界上,给定流速数据或给定潮位数据。本研究中,小区域模型的水域边界条件由经过数据验证后的大区域模型计算得到。
3.3.2 闭边界条件
本次模拟模型的闭边界条件为水-陆边界条件,即海底管道所处的海域与深圳近岸陆地组成的边界条件。在此边界上,水质点的法向流速为0,即:Vn=0。
3.3.3 表面边界条件
本次模拟模型的表面边界条件代表风场、气压场对水体自由表面的影响,本模型中采用已有的风应力参数化方法,对低风速、中风速及高风速条件下的风场数据进行拟合,表面边界条件的表达式如下:
式中:Cd为风力拖曳系数;w10为海平面上10 m 处的风速,m/s;ca=0.001 255、cb=0.002 425、wa=7 m/s、wb=25 m/s为经验系数。
3.3.4 底部边界条件
本次模拟模型中,底部边界条件通过输入曼宁系数M确定,表达式如下:
3.3.5 干-湿边界条件
本次模拟模型中,对干-湿边界条件的处理采用的是动边界方法,在模型计算过程中,模型系统会监视每一个网格单元的水深变化值,依据对干边界(Dry)、漫水区(Flood)及湿水区(Wet)预先设定的不同水深值,实时判断出计算单元的水深类型,并采取相应的处理方法[16,17,20-22]。如果监测到网格单元的水深值小于干边界值,则系统将把该网格单元从计算中移除,输入该单元的动量通量为0[21-25]。
4 工程实测验证
为了验证上述海底管道路由区水动力冲淤数值模拟模型的有效性,将模型的数值计算结果与采用多波束测深仪获取的工程实测结果进行对比。
依据靠近海底管道地理位置附近的赤湾站和珠海站历年的水文资料统计分析结果,参考JTS/T 231—2—2010《海岸与河口潮流泥沙数值模拟技术规程》筛掉小波高数据,将代表性浪向波高加权得到研究海域的年均波浪场数据[24-26]。
正常海况下(以2019 年对管道路由区的现场潮位、潮流、悬沙、表层沉积物调查数据以及赤湾站、珠海站的年均波浪、风速等数据为基础),采砂区与管道路由区在现状水深条件下1年的水动力冲淤特征模拟模型计算结果显示:
采砂区形成后,对周边海域冲淤环境的影响主要体现为采砂坑的南、北两侧以及东侧为冲刷环境,海底局部冲刷强度约为1 m/a,采砂坑内为淤积环境,海底最大淤积强度达1 m/a以上。
采砂区形成后,在水动力作用下,采砂坑北侧边界向西北方向扩展,远离管道走向,对管道安全无影响。采砂区南侧边界向东南方向扩展,与管道走向有一定重叠,导致铜鼓水道附近KP 12-KP 14 段管道路由区海底侵蚀加剧,该段侵蚀强度达到约0.2 m/a,其他管道段仍呈现淤积特征。需特别注意的是,与管道中部平行的、新形成的采砂区东侧边界形态较为曲折,与该区域的涨、落潮主流向斜交,导致水动力冲淤作用会对该段采砂区边界的突出部分进行冲淤调整,引起凸体局部冲刷,从而使得采砂区东侧边界向靠近管道方向扩展。
冲刷1 年后,采砂区北侧边界呈环状向西北方向扩展1 km,采砂区南侧边界呈环状向东南方向扩展1 km,采砂区东侧边界向靠近管道方向扩展40 m,扩展段为与管道KP 4+120-KP 11+120段之间平行的部分,距管道最近段为KP 5+300-KP 5+600 之间的部分。正常海况下管道路由区模拟计算1年周期后的水动力冲淤特征如图6所示。

图6 基于数值模拟模型计算的管道路由区水动力冲淤特征图(图中红线为管道位置)
将2019—2020 年两期次、间隔1 年的管道路由区海底地形实测结果与数值模拟模型计算1年的结果进行对比验证显示,实测数据与模拟值具有很高的符合程度,数值模拟的预测准确度达95%以上,表明数值模型有效。实测数据与数值模拟值对比见表2。
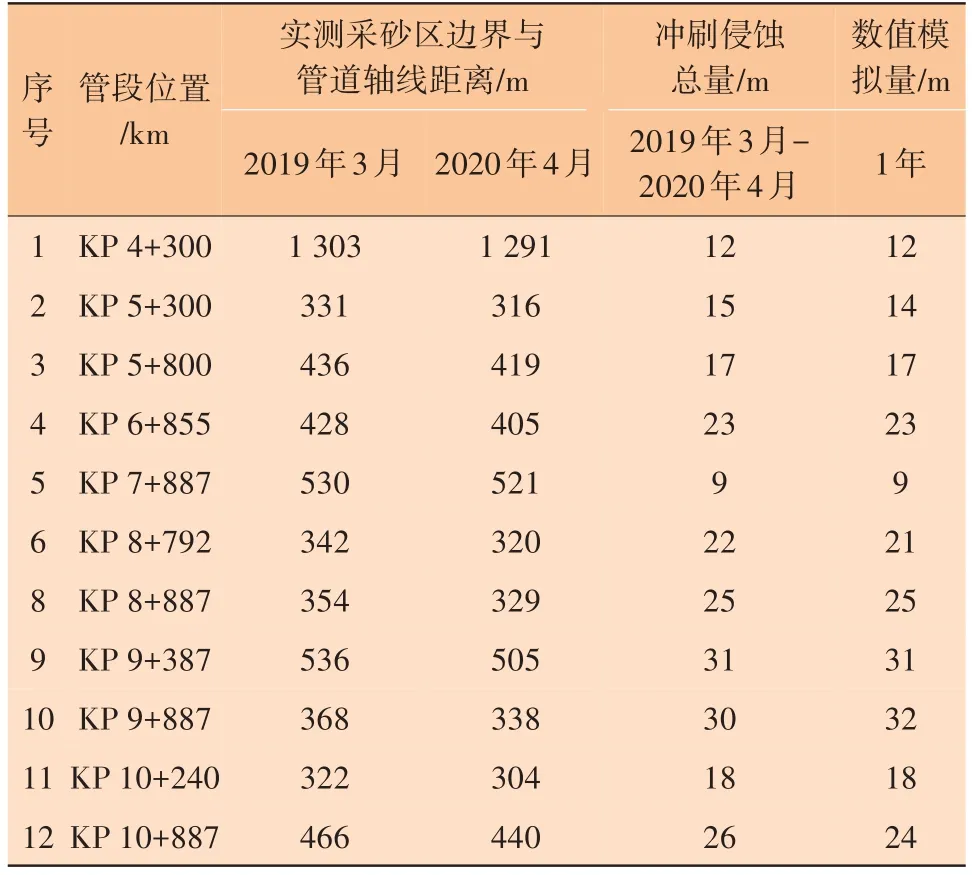
表2 管道路由区部分典型位置的冲淤变化实测值与数值模拟值对比
5 结论
针对深圳沿海某海底管道路由区的海床破坏引起海底冲刷、水动力侵蚀变化以及冲淤特征演化等影响管道路由区安全的问题,研究了适用于该海底管道路由区特征的水动力冲淤特征数值模拟方法,通过模型模拟了正常海况下一年周期的海底冲淤变化,并根据2019—2020 年两期次、间隔1年的海底地形冲淤变化实测数据对数值模拟模型进行了验证,得出以下结论:
1)研究提出了基于水动力数值模型分析的路由区冲淤特性计算方法,设计了二维水流泥沙数学模型,实现了符合管道路由区工程实际的数值模拟计算。
2)利用管道路由区实测的水深地形、潮流、悬沙、表层沉积物组成数据确定的不同尺度数值模型的边界条件在模拟计算中有效,模拟了不同模型尺度下管道路由区的冲淤状况,路由区现场实测海底地形变化数据验证了模型方法的正确性与可靠性。
3)形成的技术方法可解决海底管道路由区不同尺度范围内水动力冲淤动态变化影响的分析难题,可为海底管道保护与运维评估提供技术支持。
