基于WOSA-BP 的车辆动态称重算法研究*

袁 科，许素安，富雅琼，徐红伟

(中国计量大学机电工程学院，浙江 杭州 310018)

随着我国社会经济的发展，道路运输已位列世界前列。与此同时，超载现象也愈发严重。车辆超载运输不仅容易引发交通事故，并且对大气污染、公路设施造成永久损坏，形成恶性循环[1]。检验车辆是否超载有静态和动态称重两个方案。静态称重技术比较成熟，检测精度高，但存在着检测速度慢，现场安装复杂，容易造成交通拥堵风险的缺点。与前者相比，动态称重可以对行驶的车辆直接进行动态测量，无需停车，大大提高了测量效率[2]。但是，动态称重精度要低于静态称重，这也导致了动态称重的应用受到限制[3]。因此，研究如何提高车辆的动态称重系统精度是十分重要的。王锦芳等[4]的研究表明，动态称重精度主要受到路况(路面激励)、环境温度、车轴负载、车速、车辆振动和车辆系统结构的影响。除此之外，传感器和称台系统对应力的反应速度、传感器非线性特征引起的误差等因素也会导致动态称重系统的称重精度下降。由于动态称重系统的称重精度影响因子很多，互相之间也无线性特征关系。所以，很难确定动态称重系统与各影响因素之间的联系。人工神经网络(ANN)具有很强的自学习能力，对非线性问题的处理效果很好，适应范围很广。它普遍应用于计算机科学、数据处理、语言识别、企业管理等领域。因此将神经网络应用于拟合称重精度是可行的。在国内外已经有一些研究人员已经使用神经网络来提高车辆动态称重的精度。Arturo 等[5]将多层前馈人工神经网络应用于车辆动态称重，分析证明了人工神经网络方法比传统的基于平均值的校准方法具有更高的精度。Zhou等[6]用多层BP 神经网络估计移动车辆的静态车重，使样本的最大误差小于5.18%。但由于它受初始阈值和权值影响较大，导致训练效果不稳定，需结合其他优化算法进行改进。群体智能优化算法如鲸鱼优化算法(WOA)、粒子群算法(PSO)、天牛须搜索算法(BAS)等可以调整BP 神经网络的初始权值和阈值，使操作系统减少陷入局部最优的可能性。崔萌洁等[7]使用PSO 算法优化BP 神经网络，利用粒子群算法的全局寻优能力找到神经网络的权阈值，有效降低了温度对扩散硅压力传感器的影响。刘晓坤等[8]将天牛须搜索算法(BAS)应用于BP 神经网络，在一定程度上提高了BP 神经网络的训练能力。上述模型能一定程度上优化BP 神经网络的训练效果，但是在实际应用中存在许多不足，如粒子群算法容易产生早熟收敛，且不是全局收敛；天牛须搜索算法收敛速度相对较慢，在处理多维复杂问题时，容易搜索失败。Wang 等[9]将WOA 引入BP 神经网络，应用于信用卡欺诈检测技术的研究，仿真结果表示，WOA-BP 算法具有比较高的检测速度和收敛速度。在WOA 优化能力出众的基础上融合了模拟退火算法的全局寻优能力，鲸鱼退火算法应用于不同的领域。Ahmed 等[10]利用WOSA 算法来寻找部分遮光条件下的光伏系统的最大功率点，提高了光伏系统在部分遮光条件下的性能，并且与WOA和SA 算法进行比较，验证了WOSA 算法的越性。Ekinci 等[11]利用WOSA 算法优化了PID 控制器参数，成功提高了磁悬浮系统的性能。

本文针对BP 神经网络的不足和WOSA 算法的优越性，分析并提出了一种基于WOSA 算法优化的BP 神经网络车辆动态称重模型。先通过小波变换对动态称重信号进行预处理，然后创建了一个由WOSA 算法优化的BP 神经网络来处理车辆动态称重信号，以提高系统称重精度。最后，通过鲸鱼退火算法(WOSA)对比粒子群算法(PSO)、天牛须算法(BAS)以及鲸鱼优化算法(WOA)优化的BP 神经网络模型预测数据，并对其预测能力进行比较，得出结论。

1 动态称重系统的结构及原理

动态称重系统结构主要包括云平台、地感线圈、车检器、整体式称重台、信号处理电路、工控机以及嵌入式称重传感器等。图1 为动态称重系统的结构分布图。

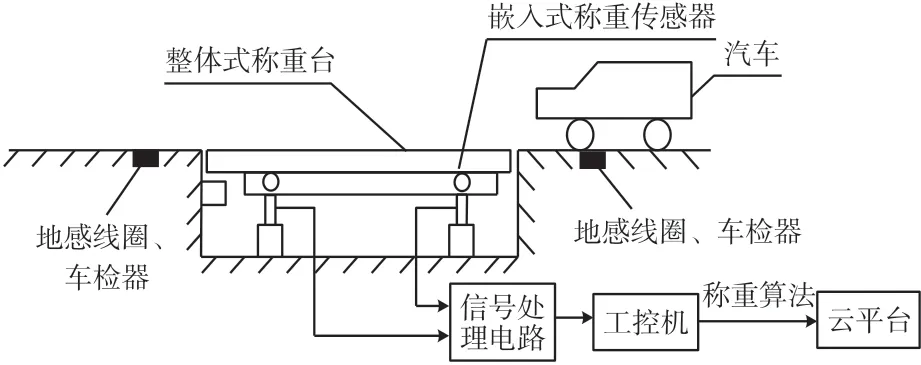
图1 动态称重系统结构分布图

系统安装和工作流程:①称台和公路采用嵌入式连接，表面呈一水平面且无缝隙，如图2 所示。②一条车道上平行放置两个称重平台，每个平台有两个对称的工型梁，每个工型梁安装两个称重传感器。③当行驶车辆经过秤台时，触发前地感线圈。嵌入式称重应变传感器受压产生形变，将重量信号转换为电压信号。④信号处理电路将其进行放大、滤波以及A/D 转换。⑤车辆离开后地感线圈，车检器输出下降沿信号。⑥工控机计算出车重、车速和车轴数等参数，并通过网络将这些参数上传至云平台。

图2 整体式称重台设计图

2 动态称重信号的预处理

车辆动态称重系统的实验测试环境较为理想，但系统安装运行的实际工作环境要恶劣许多，会有更多产生噪声信号的干扰源。为了减少噪声干扰信号的影响，需要对信号进行滤波处理。车辆动态称重离散信号主要包括低频噪声干扰和高频噪声干扰，前者居多。但是影响称重精度的主要是后者。本文采用离散小波变换来对称重信号进行预处理。

Daubechies 小波函数(简称dbN)由于对不规则信号比较灵敏，在信息研究中使用很普遍。其中，N为dbN 小波函数的阶数。离散函数f(t)二进制离散小波变换公式为:

式中:m为伸缩因子，(2mt-2n)为ψ(2mt-2n)的共轭复数。n为平移因子，为离散时间参数。每一个m值代表着一种频率的带通滤波器。因此，通过选取不同的m值能够依次逐渐分离出不同频率的噪声以及称重信号。

本文动态称重系统设置的采样率为2 000 Hz，通过MATLAB2017b 进行实验仿真，以两轴汽车为例，在试验场地采集到的称重信号频段有如下特征:

①频率在1 000 Hz～2 000 Hz 的信号为称重系统本身的误差，可以通过算法完全消除。

②频率在500 Hz～1 000 Hz 的信号为汽车行驶过程中汽车发动机运转产生的干扰，需要进行滤波处理。

③频率在250 Hz～500 Hz 的信号为汽车通过秤台时车辆与汽车衡共振所产生的扰动，需要进行滤波处理。

④频率在0～250 Hz 的信号为汽车通过称重平台时秤台受汽车本身质量的影响产生的受迫振动，其中包含动态噪声信号。动态噪声信号对称量结果有较大的影响，但受迫振动信号是计算动态车重的关键，故该频段的信号需要全部保留，无法进行小波去噪处理。

通过分析采集到的称重信号具有的特点，选择的小波函数应该具有以下特性:信号处理使滤波器具有线性相位的对称性，对信号重构获取平滑曲线的正则性，最终选取Daubechies4 小波对信号进行处理。通过db4 小波基函数多层分解称重信号，可以降低噪声对称重信号的影响，从而得到更准确的动态称重信息[12]。设置分解层数为5，公式为:

式中:wavedec()是小波分解函数，x5为被分解的函数且分解层数为5。db4 表示采用的小波分解函数。

[C，L]存储分解后的近似与细节系数:ca5，cd5，cd4，cd3，cd2，cd1。图3 为五层小波分解细节波形图。

图3 五层小波分解细节波形图

从图3 可以看出小波分解可以有效地分离数据中高频信号，高频干扰随层级的增大而减小。其中cd1 和cd2 主要是称重系统本身的噪声，cd3 和cd4是汽车发动机运转产生的干扰，cd5 是秤台、传感器组成的汽车衡共振扰动噪声，ca5 为称重过程中产生的受迫振动也就是目前滤波所需要的线性变化信号。

小波变换处理前后的波形分别如图4 和图5所示。

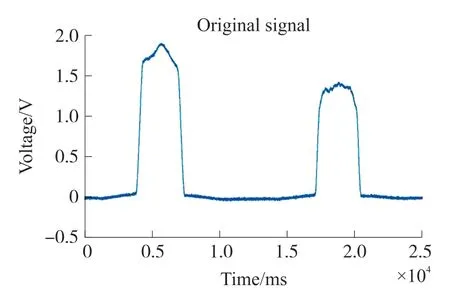
图4 小波变换去噪前波形

图5 小波变换去噪后波形

根据图4 和图5 中可知，去噪后的波形中的高频噪声明显减少。结果表明，小波变换降低了噪声的干扰，使波形更加接近真实波形。

3 WOSA-BP 算法

3.1 BP 神经网络

BP 神经网络因具有很强的非线性映射能力，如今研究已比较成熟，被广泛应用于土木工程、运动控制参数估计、机器视觉等领域[13]。BP 神经网络的结构如图6 所示。

图6 BP 神经网络的结构图

图6 中，x、h、y分别代表输入层、隐藏层、输出层节点。ωij表示输入层到隐含层的权值，ωjk表示隐含层到输出层的权值.

3.2 鲸鱼优化算法

鲸鱼优化算法模拟了鲸鱼螺旋气泡网进食策略，具有可操作性强、建模所需设置参数少、寻优效果好且速度快等优势[14-15]。鲸鱼捕食有三种方式:搜索捕食、收缩包围和螺旋式狩猎。这里将三种方式进行融合数学建模。

收缩包围和搜索捕食一起统称为包围猎物。凭借算法公式的参数A控制切换。

当参数｜A｜＞1 时，鲸鱼算法处于搜索捕食阶段，鲸鱼个体暂时偏离原目标，以此提高捕食能力，使得WOA 有一定的全局搜索性能。算法建模公式如下:

式中:a为收敛因子，i表示迭代次数，M为最大迭代次数，r∈[0，1]为随机数，是当前种群中随机单个鲸鱼个体所在的位置。

收缩包围和螺旋式狩猎一起统称为发泡网狩猎攻击。设置随机数p控制随机切换，具体如下:

式中:b为常数(默认取1)，l为随机数且l∈[-1，1]。为当前最优的鲸鱼位置，表示当前鲸鱼的位置。p为[0，1]上的随机数。

3.3 鲸鱼退火算法

鲸鱼退火算法是WOA 和SA 算法的结合。模拟退火算法核心在于Metropolis 准则，在随机搜索中，不仅能够接受最优值，还以概率P接受邻域目标值较大的劣质解[16-17]。Metropolis 准则参数公式如下:

式中:f(Xi)为第i次迭代时的适应度函数值，t为当前温度。

由上式可见，在其他条件不变的情况下，Metropolis 准则与当前温度t呈正相关，概率P随温度下降而变小。由式(8)可知，相邻两个状态呈单向相关，属于马尔科夫过程。

就像前文所说，虽然鲸鱼优化算法三种建模状态中“搜索捕食”具有一定的全局搜索能力，但是这还不够，鲸鱼优化算法依然在全局勘探能力上有所缺失，容易忽略邻域的目标最优解，从而掉入局部最优。本文提出的鲸鱼退火算法，正式在鲸鱼优化算法的基础上引入了模拟退火算法，以此加强鲸鱼算法的全局寻优能力。

主要实现方式为:在鲸鱼优化算法的每一个迭代循环中，创建一个全新的鲸鱼种群，在每一次迭代中比较新旧鲸鱼种群对应的适应度函数，新鲸鱼种群效果好就替换旧鲸鱼种群，反之，通过Metropolis准则以概率P接受。这样就大大增加了鲸鱼算法全局搜索能力[18]。这里将式(8)修改为:

式中:fnew(Xj)是第j个新鲸鱼的适应度值。

3.4 WOSA-BP 动态称重模型的建立

用WOSA 算法迭代优化BP 神经网络权重阈值。有效帮助传统BP 神经网络跳出局部最优。WOSA-BP 算法的流程如下:

①算法参数初始化。设置鲸鱼种群数量N、最大迭代次数M、随机数l、接受概率P、初始迭代次数i以及搜索空间维度D等参数，并且将BP 神经网络的误差函数f(ω)作为适应度值函数、将BP 神经网络的权重阈值作为鲸鱼个体的位置信息X＝[X1，…，Xn]。

式中:h为输出节点数量、ys、us为期望输出和预测输出。

②训练BP 神经网络，计算种群的适应度函数值。计算模拟退火算法的初始温度t0，更新a、A、C、l、p。找到并记录种群中最优个体位置Xbest，和最优适应度值f(Xbest)。

③当p＜0.5 时，若A＜1，通过式(5)的第一个公式重新确定鲸鱼位置；若A≥1，需要在当前群体范围内随机确定鲸鱼个体位置，通过式(3)更新当前鲸鱼位置。当p≥0.5 时，通过式(5)的第二个公式确定鲸鱼位置。

④进入模拟退火阶段。定义一个新鲸鱼种群，随机化鲸鱼种群个体位置信息，计算新种群的适应度值。

⑤计算更新后的原种群适应度。比较新种群中鲸鱼个体的适应度值和原种群的鲸鱼个体的适应度值。如果前者优于后者，则用新种群中的鲸鱼位置替代原种群中鲸鱼的位置。反之，则由式(9)中的概率P接受新种群鲸鱼的位置。

⑥进行缓慢退温:t＝0.9×t。

⑦记录此时的最佳鲸鱼个体Xbest及其适应度值。如果i≤M，则i＝i＋1，重复步骤②～⑦，直到满足条件为止；反之，进入步骤⑧。

⑧以最优个体值作为神经网络参数，输出最优个体位置Xbest及其适应度。

4 算法仿真结果与分析

4.1 实验数据的获取

测试实验总共选用3 辆货车(二轴、四轴、六轴货车各一辆)、分别以空载和满载各两种状态进行动态称重的测试，以模拟不同货物装载条件。实验前，对3 辆车进行静态称重，分别得到车辆的静态总重和静态轴重。测试时，试验车辆尽量以恒定的车速通过测量带，车速小于70 km/h。动态测试后，记录车辆的轴数、车速、动态车辆总重和动态车辆轴重。一共采集实验数据361 组。

根据实验数据，分别组成总重数据集和轴重数据集。总重数据集包括车速、车轴数、动态总重和静态总重。轴重数据集包括车速、轴数、动态轴重和静态轴重。

所有测试车辆的参数如表1 所示。

表1 实验测试车辆数据

4.2 实验数据的预处理

本文中，使用MATLAB 构建WOSA-BP 称重模型。使用Mapminmax 函数对输入数据和输出数据进行归一化处理。目的是提高样本的训练速度。训练结束后，对模型的预测结果数据进行反归一化处理。归一化和反归一化公式如下所示:

式中:x为动态车重测试集、xmin、xmax表示测试集的最小值和最大值、y为归一化后的数据样本。这个方法又名离差标准化。

4.3 动态称重模型的建立及参数选择

BP 神经网络的输入层分别由车轴数、车速以及动态车重三个节点组成。静态车重作为输出层节点。隐含层设置为单层6 个节点。其中，隐含层节点数n的选取参照公式:

式中:m为输入层节点数，r为输出层节点数。文中r＝1，v为常数，v属于[1，10]。由上述公式可以计算出隐含层节点数为3～12 之间，经过试凑法，当v＝4 时效果最佳。

在WOSA-BP 算法中，算法配置如下:①鲸鱼种群数量N＝31。②最大迭代次数M＝100。③搜索空间维度D＝mv＋vr＋v＋r＝31。④初始温度T＝7 000。⑤冷却因子α＝0.9。⑥BP 网络的最大训练次数为1 000，学习速率为0.1，目标误差为0.000 01。⑦选择trainlm 函数作为学习函数(学习效率高且迭代误差减小幅度较大)。⑧选择tansig 正切函数(误差较小)作为输入层到隐含层传递函数。⑨选择purelin 线性函数作为从隐含层到输出层的传递函数。

总重测试样本和总重训练样本将以1 ∶9 的比例从所有实验数据中随机选取进行模型训练。轴重测试集和轴重训练集的选取方法以及比例和总重的基本相同。

4.4 车辆总重的预测及结果分析

将WOSA-BP 称重模型、BP 称重模型和WOABP 称重模型、PSO-BP 动态称重模型和BAS-BP 动态称重模型对测试样本的预测误差进行对比。对比结果如图7 所示。

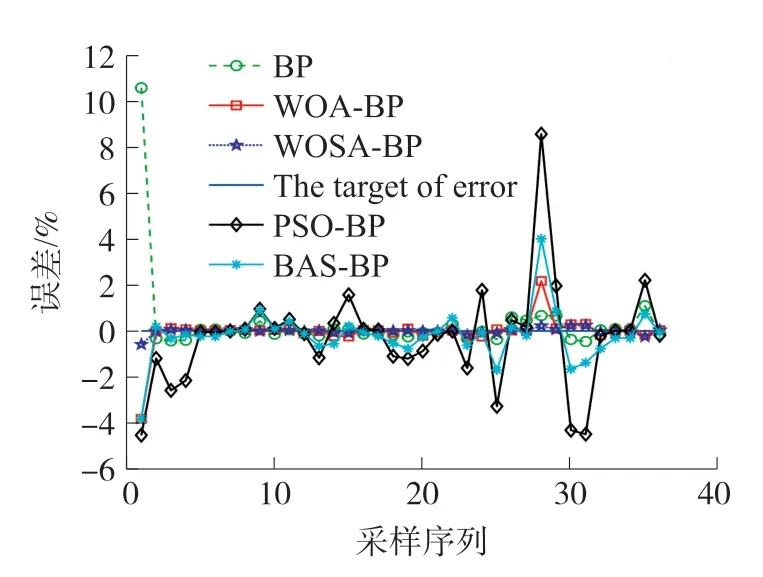
图7 不同模型的总重预测误差比较图

在图7 中，“☆”表示WOSA-BP 称重模型的预测误差，“□”表示WOA-BP 称重模型的预测误差，“○”表示BP 称重模型的预测误差，“-”表示目标误差，“◇”表示PSO-BP 称重模型的预测误差，“*”表示BAS-BP 称重模型的预测误差。从图7 中可以看出，这5 条拟合曲线里，BP 称重模型和PSOBP 称重模型由于易陷入局部最优解的缺陷，对部分样本的预测误差百分比超过了8%，预测误差较大。BAS-BP 称重模型和WOA-BP 称重模型虽然拟合效果相对较好，但是相比于WOSA-BP 称重模型，模型的稳定性不足。从WOSA-BP 模型的拟合曲线来看，通过鲸鱼优化算法和模拟退火算法模型的优势互补，预测值与静态车重能够较好地吻合，WOSABP 称重模型的预测误差明显低于其他称重模型。

五个总重模型的平均相对误差和最大相对误差对比结果如表2 所示。

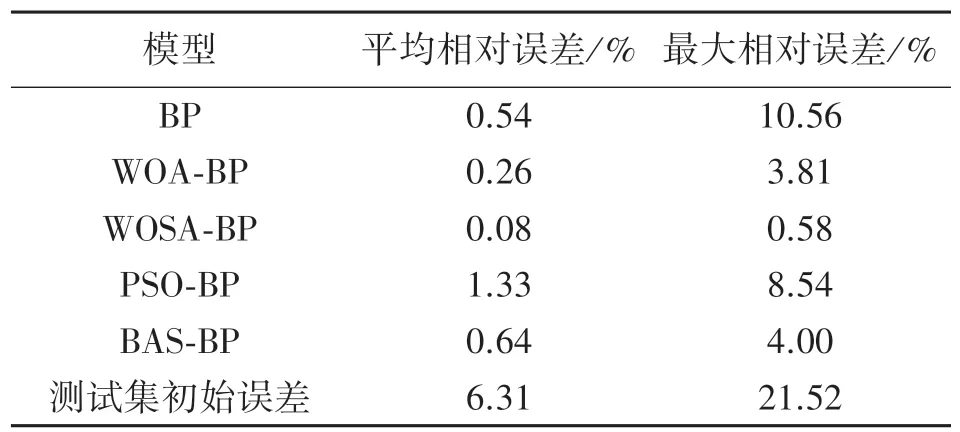
表2 五种总重模型的平均绝对误差和最大误差

从表2 可以看出，WOSA-BP 动态称重模型的平均总重相对误差和最大总重相对误差都低于PSOBP 动态称重模型、BAS-BP 动态称重模型、WOA-BP动态称重模型和BP 动态称重模型。总重测试集的平均相对误差从6.31%减少到0.08%，最大相对误差从21.52%减少到0.58%。结果表明，WOSA 算法提高了BP 神经网络的精度和泛化能力，其优化效果高于WOA 算法、PSO 算法和BAS 算法。

对PSO-BP 动态称重模型、BAS-BP 动态称重模型、WOA-BP 神经网络和WOSA-BP 神经网络的适应度值进行对比。对比结果如图8 所示。适应度值曲线的斜率代表该称重模型的寻优收敛速度，横坐标适应度值代表寻优收敛效果，曲线斜率越大、最终适应度值越小、到达最优适应度值前迭代次数越小说明效果越好，如图8 所示，PSO-BP 模型收敛速度最慢，收敛值较大，明显陷入局部最优，BAS-BP 模型以及WOA-BP 模型分别在速度和收敛效果上略优于PSOBP 模型，但效果不明显，WOSA-BP 模型寻优收敛效果最好，在迭代18 次左右趋于平稳，优化速度较快。

图8 总重适应度值的迭代比较图

4.5 车辆轴重的预测及结果分析

通过轴重训练集建立了WOSA-BP 动态称重模型、BP 动态称重模型、WOA-BP 动态称重模型、PSO-BP 动态称重模型和BAS-BP 动态称重模型。对五个模型在轴重测试集上的预测误差进行了比较。由于图线较多，这里拆分成两张图展示结果，结果如图9、图10 所示。

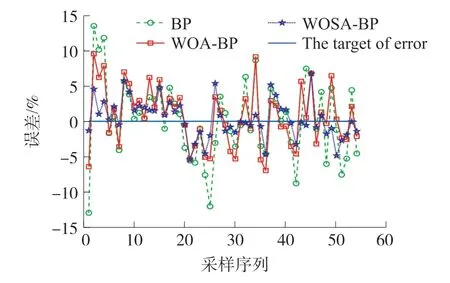
图9 WOSA-BP 与BP、WOA-BP 动态称重模型的轴重预测误差比较图

图10 WOSA-BP 与PSO-BP、BAS-BP 动态称重模型的轴重预测误差比较图

五个模型的平均轴重相对误差和最大轴重相对误差见表3。

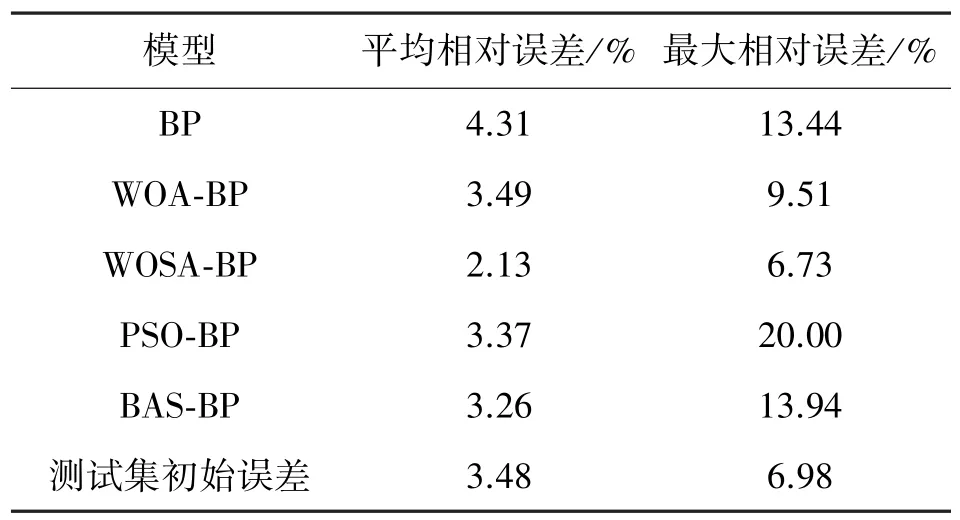
表3 五种轴重模型的平均绝对误差和最大误差

从表3 可以看出，WOSA-BP 动态称重模型的轴重预测误差比其他模型小。轴重测试集的平均相对误差从3.48%减少到2.13%，最大相对误差从6.98%减少到6.73%。从表2 和表3 的比较结果可以看出。WOSA-BP 算法对总重或轴重的预测精度更高。

5 结束语

本文运用小波变换优化分解重构了原始信号，基本去除了环境对信号的干扰。运用WOA 的局部搜索能力配合SA 算法的全局勘探特点，组合优化了传统的BP 神经网络。建立了WOSA-BP 神经网络动态称重模型，以提高车辆动态称重系统的检测精度。实验结果表明，WOSA-BP 模型优化后，测试集的轴重平均相对误差从3.48%减少到2.13%，轴重最大相对误差从6.98%减少到6.73%，总重平均相对误差从6.31%减少到0.08%，总重最大相对误差从21.52%减少到0.58%。总重的预测精度比轴重的预测精度高。同时，使用WOSA-BP 模型对总重和轴重的预测精度要高于使用PSO-BP、BAS-BP、WOA-BP 和BP 模型。这些结果验证了WOSA 算法的优越性，表明WOSA-BP 算法能更有效地提高车辆动态称重系统的精度，将总重误差控制在1%以内。