基于MPSO-BP 算法的四电极电化学气体传感器温度补偿研究*

刘 伟，鲁 露，杨文博，赵曼玉，魏广芬，2

(1.山东工商学院信息与电子工程学院，山东 烟台 264005；2.山东省高校感知技术与控制重点实验室，山东 烟台 264005)

电化学气体传感器具有测量灵敏度高、性能稳定、线性度高、寿命长、选择性好等特点，被广泛地应用于低浓度有毒有害气体、可燃气体和环境空气等定量监测领域[1-2]。但是电化学气体传感器在工作时易受环境温度影响，传感器的灵敏度和零点电流随环境温度变化，从而降低了检测精度。因此，电化学传感器温度补偿成为当前气体传感器研究的热点之一[3-5]。目前气体传感器的温度补偿从结构上分为硬件补偿和软件补偿两种方法，其中常见的软件补偿方法有查表法、曲面拟合法及BP 神经网络等方法[6-7]。其中BP 神经网络方法虽然精度较高，但存在初始权值及阈值难以确定、收敛速度慢、易陷入局部极小等缺点[8-10]。

本文提出一种基于改进的粒子群优化PSO(Particle Swarm Optimization)算法对BP 神经网络进行参数优化的方法，即利用PSO 强大的全局搜索能力、收敛速度快、稳定性好等特点针对BP 神经网络参数进行改进和筛选，使优化后的BP 神经网络具有克服局部极小、更快收敛等能力；采用优化后的BP 神经网络对四电极电化学气体传感器进行温度补偿，可显著提高补偿精度。

1 温度补偿测试系统

1.1 四电极电化学气体传感器工作原理

与常规的三电极电化学气体传感器不同，四电极电化学传感器除了工作电极WE(Worker Electrode)、对电极CE(Counter Electrode)和参考电极RE(Reference Electrode)三个电极之外，还有一个辅助电极AE(Auxiliary Electrode)，该电极用于补偿零点电流。四电极传感器工作时，工作电极WE 与对电极CE 之间发生氧化或还原反应形成的电流与被测气体浓度呈线性关系；参考电极RE 维持稳定工作电压；辅助电极AE 不参加反应，不会产生基线漂移。将工作电极WE 信号值与辅助电极AE 信号值相减，再与灵敏度系数相乘即可计算出被测气体浓度。四电极电化学传感器具有较高的测量精度和分辨率，广泛用于低浓度的大气环境监测。但是，四电极电化学气体传感器的测量精度极易受环境温度影响[11]。

1.2 系统组成

本文设计的四电极电化学气体传感器温度补偿测试系统，其结构如图1 所示。

图1 温度补偿系统结构图

整个系统由配气系统、密封气室、电化学气体传感器、温湿度传感器、信号调理电路、主机系统及PC上位机组成。主机系统采用STM32F103VET6 微处理器，扩展24 位高分辨率AD 转换芯片AD7190。配气系统由青岛佳明公司设计，可配制任意浓度标准气体。温度测量采用瑞士Sensirion 的SHT30 数字传感器。信号调理电路采用3 片高精度运放OPA2335 构成二级运放电路，将工作电极WE 和辅助电极AE 输出的微弱纳安级电流信号放大为0～3 V 电压信号输入到ADC。信号经滤波平滑处理后由串口发送至上位机，进行温度补偿算法测试、数据存储及显示。传感器系统封装在一个方形密封气室中，采用泵吸式方法，气体流速为0.5 L/min，使被测气体与传感器充分接触，以发挥气体传感器的最佳性能。研制的气体传感器测试系统装置如图2所示。

图2 气体传感器测试系统

2 算法原理

2.1 BP 神经网络

BP 神经网络包含输入层、隐层和输出层。以3层神经网络为例，BP 网络在训练时会随机设定初始权值和阈值。设输入矢量X＝(x0，x1，…，xn)T，输出矢量为Y＝(y0，y1，…，yn)T，隐层输出矢量为O＝(o0，o1，…，ol)T，期望输出矢量D＝(d0，d1，…，dm)T。其中n，l，m分别表示输入层，隐层和输出层的神经元个数。

输入层至隐层的权值矩阵和阈值矩阵为:

隐层至输出层的权值矩阵和阈值矩阵为:

BP 神经网络训练的一般步骤为:

①网络初始化:选择结构合理的网络，设置随机分布的权值和阈值；②给定输入样本和期望输出，对每个样本计算各层的实际输出和节点误差；③修正权值和阈值；④输入新的样本，直至目标函数误差最小。

2.2 粒子群优化算法及参数设置

粒子群优化算法(PSO)源于对鸟群捕食行为的研究，基本思想是通过群体中个体之间的协作和信息共享来寻找最优解[12-15]。PSO 具有实现容易、收敛速度快、精度高等优点[16-18]。

假设在一个m维搜索空间中，由n个粒子组成的种群X＝(X0，X1，…，Xn)，第i个粒子表示为一个m维的矢量Xi＝(xi1，xi2，…，xim)T，即在m维搜索空间中的位置。根据目标函数计算每个粒子的适应度值。第i个粒子的速度为vi＝(vi1，vi2，…，vim)T，个体极值为pi＝(pi1，pi2，…，pim)T，种群的群体极值为pg＝(pg1，pg2，…，pgm)T。PSO 算法的粒子速度和位置的更新公式为:

PSO 算法主要的初始化参数包括加速度因子和惯性权重。当c1较大时，会使粒子过多地在局部范围内徘徊；而当c2较大时，则又会促使粒子过早收敛到局部最小值。因此须有效地控制粒子的飞行速度，提高算法的搜索能力，保证算法达到全局探测与局部开采两者间的有效平衡。本文采用Clerc 提出的带收缩因子的PSO[19]，其粒子速度迭代方程为:

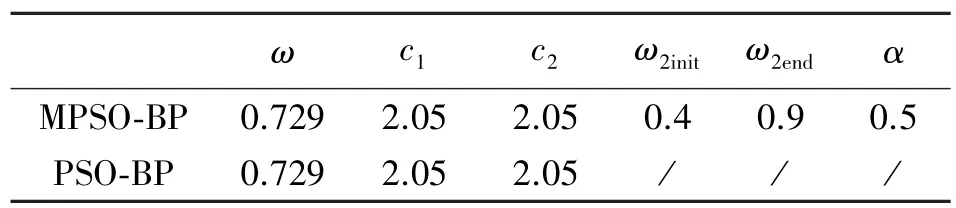
表1 MPSO-BP 和PSO-BP 初始参数

2.3 改进PSO 算法

传统的PSO 算法在后期存在收敛速度慢、易陷入局部极小值问题，为了解决这些问题，本文在带收缩因子的PSO 基础上提出了一种新型的改进算法MPSO(Modified Particle Swarm Optimization)，即引入位置增量项和惯性权重全局修正因子，具体形式如下:

ω2参数在保留了传统PSO 算法的全局搜索能力和局部搜索能力的同时，对速度的修正量进行全局微调，其动态变化采用二次曲线，如式(10)所示:

2.4 基于PSO-BP 算法的温度补偿模型

利用改进的PSO 算法优化BP 神经网络的权值和阈值，构建四电极电化学传感器的温度补偿的一般模型，其具体流程如下:

①构建BP 神经网络。输入为温度T和传感器经调理后输出的2 路电压，输出为补偿后的电压。所以输入维数n＝3，输出维数m＝2。由于隐层神经元个数的选取暂无充足的理论，因此本文采用式(11)所示的经验公式多次实验求得。首先设置较少的节点，对网络进行训练并保存模型结构；其次逐渐增加节点数，重复上一步骤并比较两次模型的均方误差；直至均方误差最小，所对应模型的隐层神经元个数为本文最终的取值。本文最终的隐层神经元个数l＝5。初始化权值矩阵和阈值矩阵W1、B1、W2、B2，并变换为一维数组作为PSO 算法的初始种群。

式中:n为输入节点数，m为输出节点数，α代表1～10 的常数。

②初始化PSO 算法的种群个数。每个粒子的维数为n×l＋l＋l×m＋m，此处为32。设定粒子的初始位置和速度、惯性权重范围等参数。

③将BP 神经网络的训练误差函数作为适应度函数。输入样本数据，计算每个粒子的适应度值，记录个体极值和群体极值，并按式(8)和式(9)更新粒子位置和速度，然后继续迭代直到满足性能要求。

④将PSO 算法优化后得到的W1，B1，W2，B2，作为BP 神经网络的初始参数对样本进行训练。

3 实验结果与讨论

3.1 样本数据

本文选用英国Alphasense 公司的B4 系列四电极电化学气体传感器H2S-B4，量程为0～100×10-6(经信号调理电路变换后实际量程为0～15×10-6)，灵敏度为1 450 nA/10-6～2 050 nA/10-6，工作温度为-30 ℃～50 ℃。传感器的输出-温度曲线如图3所示，可见传感器的输出受温度变化的影响较大。

图3 H2S-B4 传感器输出－温度特性曲线图

在不同温度下，利用搭建的测试系统采集样本。首先通入不同浓度的标准H2S 气体，待ADC 数值稳定后读取响应值。表2～表4 分别列出了4×10-6，6×10-6，8×10-6三种浓度下的部分实测样本数据。从表中看出，样本数据符合传感器输出-温度特性曲线，表明测试系统采集的数据是可靠的。

表2 H2S-B4 气体传感器的测试数据(4×10－6)

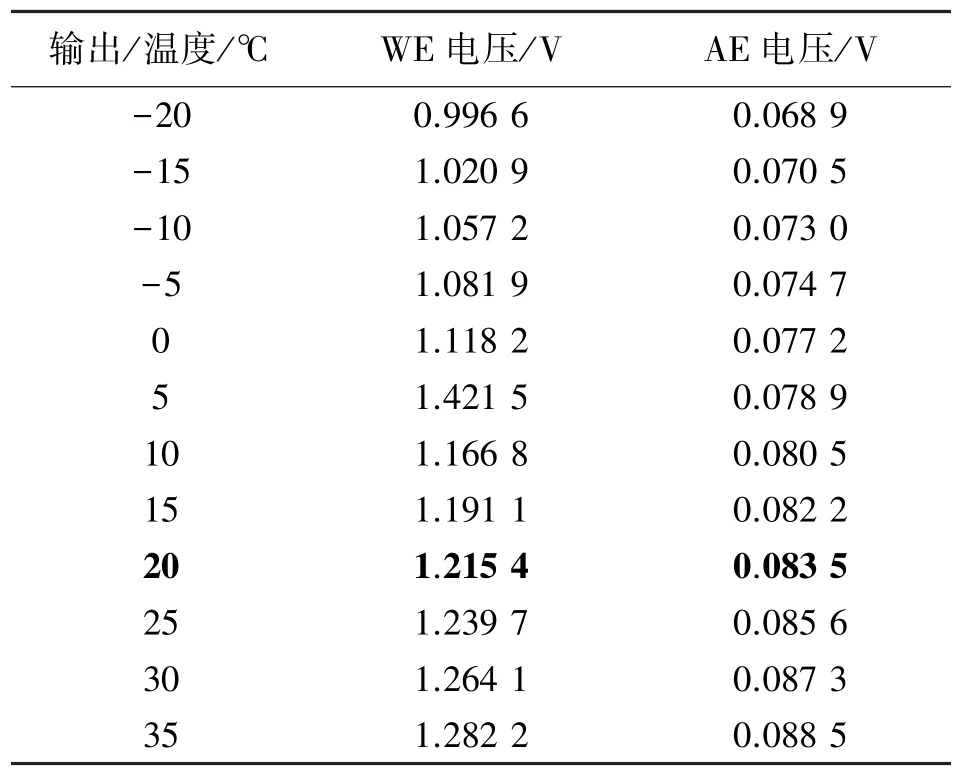
表3 H2S-B4 气体传感器的测试数据(6×10－6)

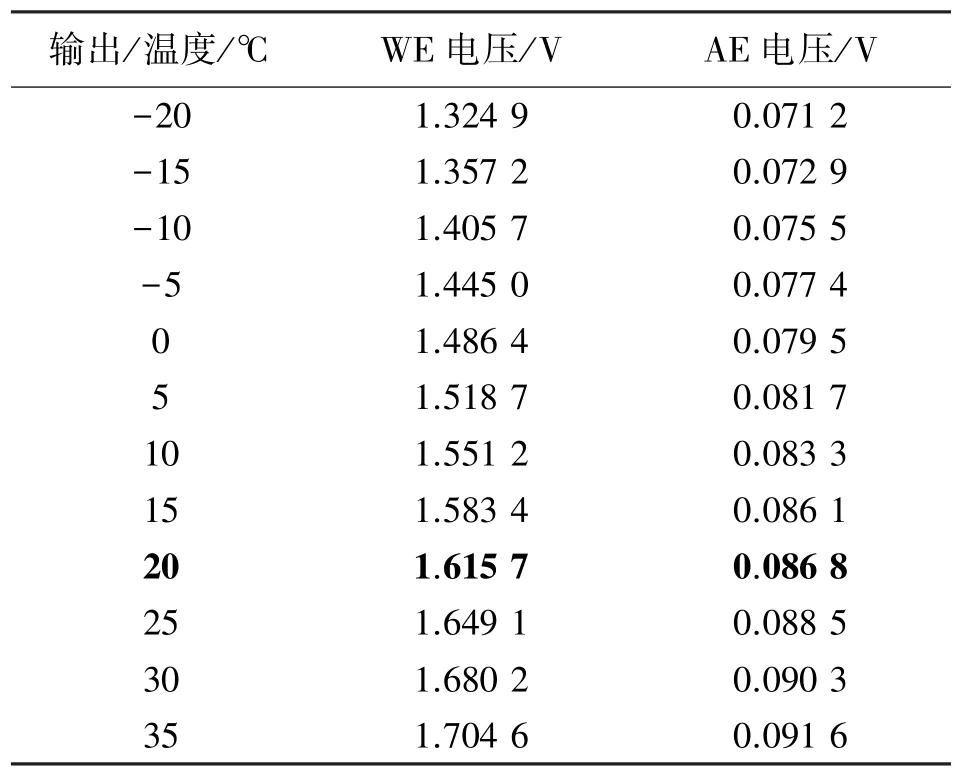
表4 H2S-B4 气体传感器的测试数据(8×10－6)

3.2 样本数据预处理

不失一般性，采用随机法产生训练集样本和测试集样本，即从全部样本中随机产生50 组作为训练集，5 组作为测试集。将样本中传感器在20 ℃时的测量数据作为目标输出。为了加快训练速度，同时消除不同输入之间数值的差异，采用式(12)将样本数据归一化到[0，1]区间:

3.3 温度补偿结果及分析

为了验证MPSO-BP 算法的稳定性、收敛速度等性能，本文采用最小二乘曲面拟合、BP 神经网络和PSO-BP 网络进行性能对比。

其中，最小二乘曲面拟合方法选择二元二次多项式作为拟合曲面模型，其表达式为[7]:

式中:x是温度数据，y是电极电压实测数据，z是电极电压目标数据。p20，p11，p02，p10，p01，p00为待定系数。以使曲面拟合模型的误差平方和达到最小为原则，利用样本数据集求解二元二次多项式的待定系数。表5 列出了利用4×10-6浓度的实测样本数据求解得到的待定系数。

表5 拟合曲面模型待定系数(4×10－6)

采用SSE(误差平方和)、RMSE(均方根误差)、R-square(确定系数)指标来评估曲面模型的拟合效果。表5 待定系数对应的评估指标如表6所示。

设BP 神经网络的结构为3-5-2，最大迭代次数100，目标误差为1e-4。MPSO-BP 和PSO-BP 算法的种群规模为30，进化次数为100 次。将测试样本输入到训练好的神经网络模型中得到温度补偿结果。四种补偿方法对工作电极WE 和辅助电极AE的误差如表7 所示。式(14)和式(15)给出了二者的计算方法。

表7 四种补偿方法精度比较 单位:%

式中:p为补偿结果，q为20 ℃下的对应电极电压，n代表测试集样本数，i为正整数且i≤n。

从表7 可以明显看出，使用基于BP 神经网络的三种方法相比最小二乘曲面拟合法用于四电极电化学传感器温度补偿时，精度都有了一定的提高。基于MPSO-BP 算法的温度补偿精度要显著高于其他三种方法。经过多次重复实验，所得结果几乎完全相同，这表明本文提出的四电极电化学气体传感器的温度补偿方法具有较强的稳定性和鲁棒性，补偿总体误差能够控制在0.1%以内。采集量程范围内其他浓度的样本数据，输入到训练完毕的MPSOBP 网络进行测试，与该浓度在20 ℃下的数据进行比对，也取得了较理想的补偿效果，这证明本文提出的温度补偿方法具有较强的泛化能力，能够有效消除温度变化对传感器输出的影响。

图4 为BP、PSO-BP 和MPSO-BP 三种算法的训练过程比较图。未经PSO 算法优化过的BP 网络未能在100 次迭代以内达到全局最优，存在较大的训练误差；而PSO-BP 算法和MPSO-BP 算法在100 次迭代以内均能达到全局最优，但MPSO-BP 算法明显收敛速度更快一些。

图4 三种算法训练过程比较图

4 结论

本文提出了一种基于MPSO-BP 算法的四电极电化学气体传感器的温度补偿方法，并在所设计的传感器测试系统中进行了实验验证。结果表明，相对于最小二乘曲面拟合方法、BP 和PSO-BP 神经网络方法，该方法具有较高的补偿精度和较快的收敛速度。此外，该方法还可以应用于其他类型气体传感器的温度补偿，具有一定的工程实用价值。