粒子群优化噪声参数的行人导航零速修正算法*

李 磊，苏 中，吴学佳，雷 明，王一静

(北京信息科技大学高动态导航技术北京市重点实验室，北京 100192)

随着导航定位技术的不断发展，各行各业对于位置服务的需求日益增加。行人导航是导航定位领域的重要课题之一，行人导航系统(Pedestrian Navigation System，PNS)在军用和民用领域都具有重要作用[1]。目前，成熟的行人导航系统大部分仍基于基础设施，如全球导航卫星系统(Global Navigation Satellite System，GNSS)、超宽带和无线局域网等，但对于地下遮蔽空间、封闭建筑物内部等环境，易受到信号遮挡、基础设施损毁或设备需预先布置等条件约束，上述行人导航系统通常难以实现[2]。此类复杂环境下，主要应用惯性测量单元(Inertial Measurement Unit，IMU)的自主定位定向技术成为行人导航的研究热点。随着微机电系统(Micro-Electro-Mechanical System，MEMS)的迅速发展，MEMS-IMU 成为复杂环境下行人自主定位定向的主要设备[3]。由于惯性器件本身存在漂移，定位误差随时间迅速累积[4]。行人惯性导航系统通常使用零速修正(Zero Velocity Update，ZUPT)方法修正定位误差，ZUPT 要求将IMU 固定于行人足部，检测足部静止阶段，再通过扩展卡尔曼滤波(Extended Kalman Filter，EKF)利用零速区间的速度误差作为量测来修正捷联解算的结果[5]。田晓春等[6]构造了一种小波系数介于软硬阈值之间的连续小波阈值函数，对MEMS 陀螺仪信号进行降噪后应用于行人导航系统，通过实验对比了不同阈值法去噪后的陀螺仪信号，但未进行行人导航实验。余志鹏等[7]采用秩卡尔曼滤波来适应非高斯噪声对系统的影响，在时间更新前进行秩采样，再使用采样点集进行卡尔曼滤波，在室内环境下实验证明行人导航系统定位精度有所提高。

对于使用EKF 实现行人ZUPT 方法，系统建模误差和测量环境的不确定性对滤波器性能有重要影响，上述方法考虑了惯性器件在使用中产生的噪声信号，而滤波器中合适的噪声参数也能够有效提高行人惯性导航定位精度，但噪声参数通常未知或给定的参数不适用，将导致定位误差较大。刘韬等[8]利用Sage-Husa 滤波和Huber 函数建立自适应扩展卡尔曼滤波(Adaptive Extended Kalman Filter，AEKF)，分别对系统过程噪声协方差Q和量测噪声协方差R进行在线修正并应用于室内无人车定位，实验结果表明仅在线修正Q时平均误差反而会增大。胡高歌等[9]针对过程噪声协方差的不确定问题提出了一种基于极大似然估计的无味卡尔曼滤波，在滤波过程中对Q进行极大似然估计并将问题转化为对Q的对角元素的估计。Yan 等[10]提出了利用递归神经网络对IMU 输出序列进行某些运动模式的识别，并通过知识库获取Q值，还提出了一种逐步增加数据子集的神经网络训练方法以提高网络的训练效率。该方法在无人机组合导航系统上取得了良好的定位精度，但行人足部相对于无人机的惯性信息更加多变，此类方法可能仍需建立足够庞大的行人惯性数据集。

本文在仅使用由三轴陀螺仪和三轴加速度计构成的MEMS-IMU 的情况下，提出了一种基于粒子群优化(Particle Swarm Optimization，PSO)的ZUPT 算法，该算法通过零速修正时最小化滤波器新息序列来优化EKF 的噪声参数，能够在零速区间自主调整过程噪声参数和量测噪声参数，得到更加精确、平滑的行人运动轨迹。本文分别使用ZUPT 算法和提出的PSO-ZUPT 算法对行人实测足部惯性数据进行解算，实现了行人自主定位定向，并对两种算法解算的运动轨迹及定位误差进行了比较分析，充分验证了所提出算法的有效性。

1 粒子群优化的零速修正算法

将IMU 捆绑于行人足部，获取惯性数据后进行捷联解算，通过零速检测识别人员足部的静止阶段后得到零速区间的速度误差量测，利用EKF 对解算结果进行零速修正[11]。噪声参数对EKF 的性能有重要影响，本文利用PSO 算法自主优化EKF 的过程噪声和量测噪声参数，实现行人惯性导航，算法流程如图1 所示。

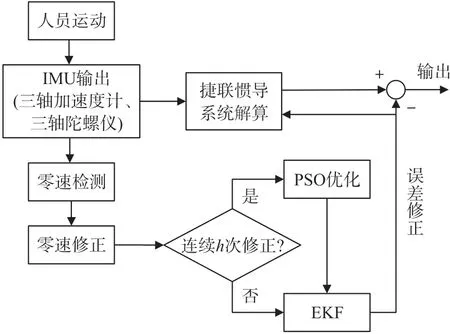
图1 算法流程图

1.1 捷联解算

捷联解算过程主要包括姿态更新、速度更新和位置更新。IMU 捆绑位置及坐标系如图2 所示，选取“北-东-地”作为导航坐标系，与地理坐标系一致。选取人员足部的“前-右-下”作为载体坐标系，IMU 固定在人员左足跟部，获取行人行走时足部的加速度和角速度信息，行人运动轨迹为长40.3 m、宽16.5 m 的矩形，IMU 输出的原始数据如图3 所示。

图2 IMU 捆绑位置及坐标系

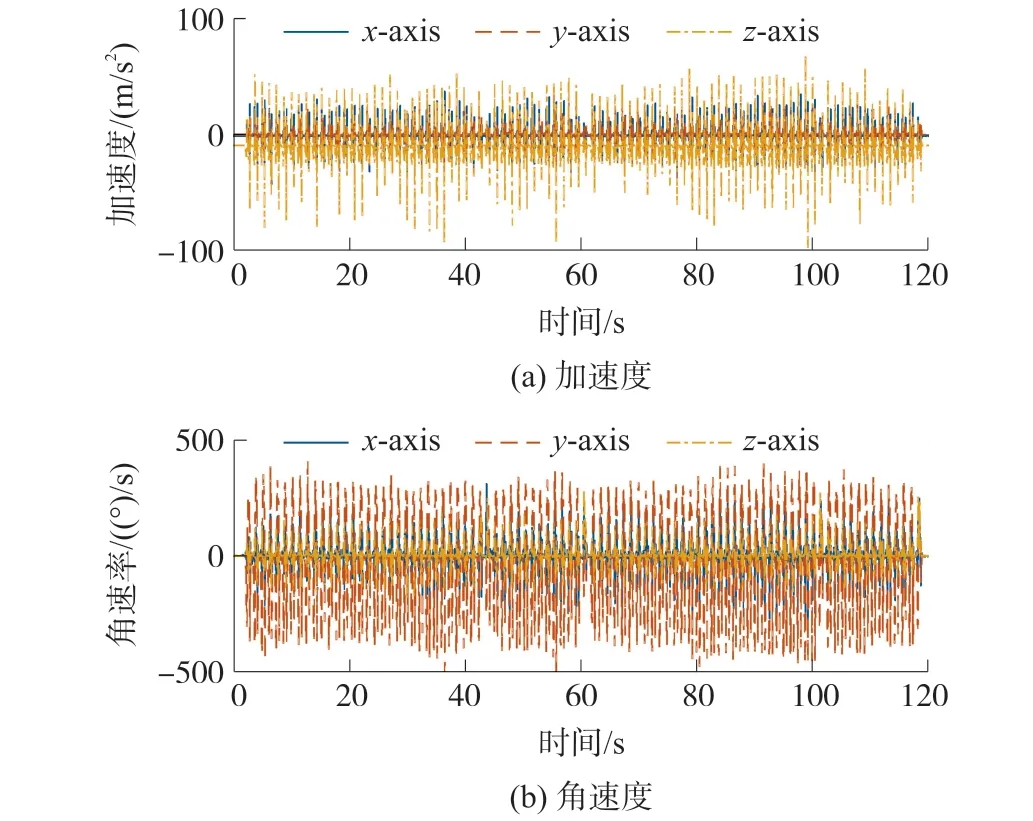
图3 IMU 输出原始数据

利用如下导航方程对行人的姿态、速度、位置进行计算:

1.2 零速检测

零速检测的主要任务是识别行人足部的静止阶段，并确定步态周期内的零速区间。使用广义似然比检测法(Generalized Likelihood Ratio Test，GLRT)进行零速检测[12]，第n组IMU 输出序列的检验统计量为:

式中:T(un)为检验统计量，W为滑动窗口大小。un为窗口内传感器输出分别为加速度计和陀螺仪的输出值，为滑动窗口内加速度计输出值的平均值，g为当地重力加速度，分别为加速度计和陀螺仪的噪声方差。Ck为零速检测输出标志位，γ为零速检测阈值。

1.3 零速修正

在行人行走过程中，足部周期性地与地面接触，ZUPT 算法将足部静止阶段的速度输出作为速度误差的量测值，使用EKF 对导航状态误差进行滤波估计，在量测更新过程中进行零速修正。

行人惯性导航系统的十五维向量Xk为:

式中:pk表示k时刻位置、vk表示k时刻速度、φk表示k时刻姿态、ak表示k时刻加速度计零偏误差，ωk表示k时刻陀螺仪零偏误差。

取导航系统状态向量的误差项δXk建立卡尔曼滤波方程:

以上15 维状态误差向量分别为k时刻的三轴位置误差、速度误差、姿态误差、加速度计零偏误差和陀螺仪零偏误差。

惯性导航系统的状态误差方程如下:

式中:Δt为采样时间，ft为加速度计测量值的反对称矩阵，b1和b2分别为加速度计和陀螺仪零偏误差的比例系数，Wk·a和Wk·ω分别为k时刻的加速度计和陀螺仪误差的随机系统动态噪声。

当行人足部处于静止阶段时，足部的理论速度应该为零，但由于存在测量误差等原因，静止阶段计算得到的速度并不为零。因此选择静止阶段的速度误差作为量测向量Zk:

由此可以得到离散时间的线性系统状态空间模型:

Wk-1和Vk分别表示过程噪声和量测噪声，其噪声统计为:

式中:Qk表示k时刻过程噪声协方差矩阵，Rk表示k时刻量测噪声协方差矩阵，δkg表示Kronecker 函数。在标准EKF 中，需设定合适的Qk和Rk。

EKF 滤波过程主要分为时间更新和量测更新，时间更新过程中，EKF 将误差状态转移到捷联解算系统中，在测量后立即将误差状态置零，并计算先验估计误差协方差矩阵。当Ck＝0 时，不进行量测更新；当Ck＝1 时，进入量测更新过程，执行ZUPT 算法。

1.4 粒子群优化的零速修正

粒子群优化算法主要思想是通过粒子之间的信息交流在候选解空间内寻找最优解。PSO 算法作为一种经典的群智能优化算法被广泛应用于求最优解与参数优化问题[13]。

本文提出的PSO-ZUPT 算法在行人足部静止时，利用PSO 优化零速修正阶段的滤波器噪声协方差矩阵参数，使滤波器能够根据行人的运动状态来自主调整参数。当零速检测判断当前状态处于零速区间时，对系统状态误差进行滤波，并执行PSO 算法，将当前的噪声协方差矩阵Qk和Rk的对角线元素作为粒子的位置输入到PSO 算法中，并利用当前量测值和估计值计算新息序列作为PSO 算法的适应度函数。通过PSO 算法来最小化量测值与预测值之间的差，从而自主更新噪声矩阵Qk和Rk[14]。根据更新后的协方差矩阵参数，分别生成协方差为Qσi和Rσi的高斯噪声Wpi和Vpi，并加入到滤波估计值和量测值中，以计算更新后的新息序列，得到优化后的最优个体。

EKF 中的过程噪声协方差矩阵Qk和量测噪声协方差矩阵Rk都为对角矩阵，Qk和Rk的优化问题可转化为其对角元素的优化问题。选取对角元素值作为PSO 算法中粒子的位置，使用PSO 算法对加速度计噪声、陀螺仪噪声及速度测量噪声的参数向量进行优化，第i个粒子的位置用σi表示:

式中:σai和σωi分别表示加速度计噪声和陀螺仪噪声参数，σvi为速度测量噪声参数。第i个粒子的速度vσi和位置σi的更新公式如下:

式中:t表示PSO 算法的迭代次数，i∈[1，M]，M表示种群个数，均为正整数。w表示惯性权重，c1和c2表示加速因子，r1和r2为[0，1]之间的随机数。bσi代表个体最优解，gb 代表全局最优解。

优化后的噪声协方差Qσi和Rσi可以通过粒子的位置σi得到:

式中:σab和σωb分别表示加速度计和陀螺仪的零位稳定性噪声，采用固定值不参与优化。

PSO 算法中适应度函数的设计决定了粒子的优化目标，计算卡尔曼滤波器新息序列的平方均值作为适应度函数并向新息序列减小的方向优化粒子，适应度函数定义为:

式中:zpij为量测值zpi的第j维数值，xpij为滤波估计值xpi的第j维数值。zpi和xpi分别引入了参数为σvi和[σaiσωiσabσωb]T的高斯噪声，其数值可以用如下表达式计算:

式中:Wpi和Vpi分别为协方差为Qσi和Rσi的高斯噪声，即:

由于对零速区间的所有时刻进行PSO 参数优化会导致轨迹解算时间过长，需设置一个连续迭代次数h，当每连续执行h次零速修正后执行一次PSO 算法。实验中，为xpid设置了不同的搜索边界来提高算法的稳定性。为提高PSO 算法的效率，还应该设置合适的最大迭代次数tmax和适应度阈值ε。图4 展示了一次PSO 参数优化过程中的最优个体适应度变化曲线，粒子群在545 次到1 000 次迭代中适应度已不再下降，根据实验经验，将tmax设为800。在算法1 和算法2 处分别给出PSO 优化噪声协方差参数算法流程和PSO-ZUPT 算法流程。

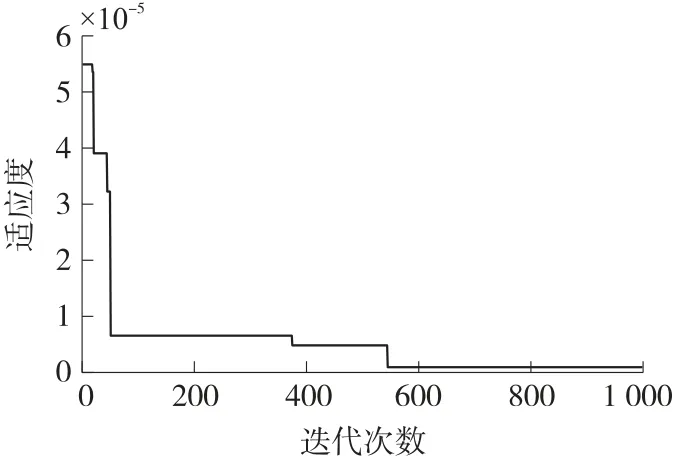
图4 PSO 最优个体适应度曲线

算法1 PSO 优化噪声协方差参数算法

算法2 PSO-ZUPT 算法

2 实验验证及分析

2.1 实验条件

实验使用图5 中实验室自研的MEMS-IMU 采集行人行走时的足部惯性数据，IMU 仅包含三轴加速度计和三轴陀螺仪，其相关技术指标如表1 所示。使用MATLAB R2018b 软件进行惯性数据解算，对算法进行验证，计算机处理器为Intel Core i7-10700K，32GB运行内存。

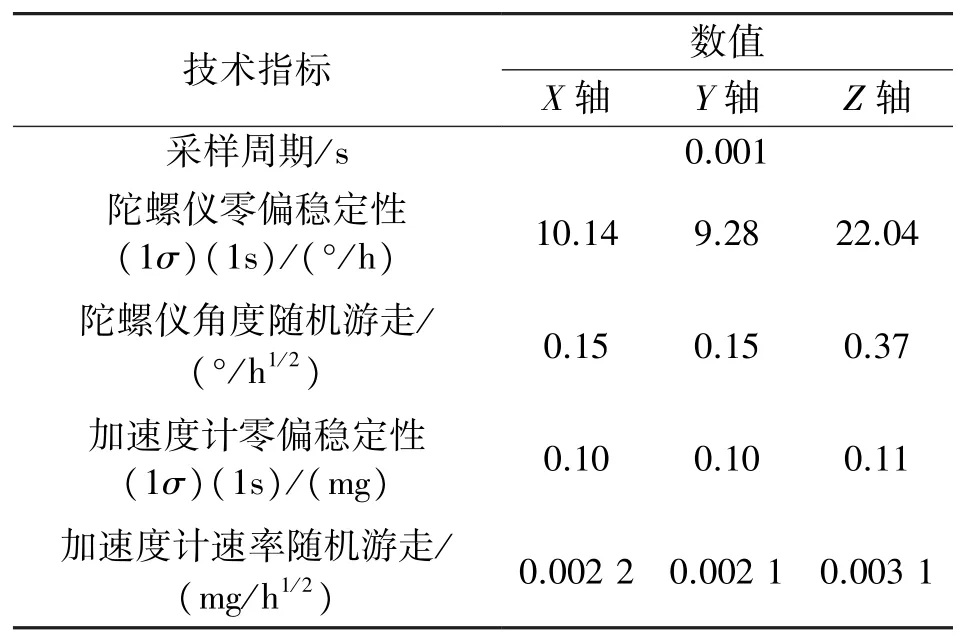
表1 IMU 技术指标

图5 MEMS-IMU 实物图

实验分别使用标准ZUPT 算法和PSO-ZUPT 算法对1.1 节中采集的惯性数据进行解算，此外，还进行了其他轨迹的行人行走实验。行人运动轨迹为沿足球场中圈连续行走3 圈回到起点，如图6 中实线圆圈所示，球场中圈半径为9.15 m，3 圈的路径总长度约为172.5 m，共采集5 组足部惯性数据。分别使用标准ZUPT 和PSO-ZUPT 两种算法进行解算，对定位结果进行分析。

图6 沿足球场中圈的运动轨迹

PSO 算法中，将M设为30，c1和c2均为2.05，零速修正连续迭代次数h设为1 000，最大迭代次数tmax为800。惯性器件噪声σai和σωi的搜索空间选为[0.01，0.5]，σvi的搜索空间选为[0.001，0.5]。PSOZUPT 算法的噪声协方差初值与ZUPT 算法的Q和R相等:

惯性权重进行线性递减，利用如下公式计算:

式中:wmax和wmin分别为惯性权重的最大值和最小值，在实验中分别设为1 和0.8。

2.2 实验结果

使用两种算法对1.1 节中惯性数据解算的结果如图7 所示。ZUPT 算法的解算轨迹与真实轨迹形状相似，但仍存在较大误差，轨迹在y 轴方向上的最大误差约为3.75 m，终点位置误差约为1.42 m。PSO-ZUPT 算法的解算轨迹更接近真实轨迹且更加平滑。经计算，最大位置误差约为1.85 m，终点位置误差约为0.64 m，与ZUPT 算法结果相比，定位误差分别减小了50.67%和54.93%。

图7 两种算法解算轨迹对比图

对5 组足球场中圈数据的解算位置误差进行计算，并给出了在MATLAB 软件下的运行时间，算法A 表示标准ZUPT 算法，算法B 表示PSO-ZUPT 算法，结果如表2 所示。平均误差为所有采样点解算位置到中圈圆心的距离与中圈半径之差的平均值，终点误差为解算轨迹终点到起点之间的距离，最大误差为所有采样点解算位置到中圈圆心的距离和中圈半径之差的最大值。

表2 中圈轨迹解算结果误差表

由表2 可知，PSO-ZUPT 算法相对于ZUPT 算法在上述三个指标上均有提高。ZUPT 算法的平均误差为0.796 m，PSO-ZUPT 算法的平均误差为0.092 m，平均误差减小了88.31%，终点误差减小了34.13%，最大误差减小了88.66%。5 组数据的行人行走时间在145 s 至151 s 之间，PSO-ZUPT 算法运行时间在86 s 至91 s 之间，相对于ZUPT 运行时间提高4.3 倍左右，但仍可以支持算法在线运行。

第1 组数据解算的运动轨迹如图8 和图9 所示，图8 为ZUPT 解算轨迹，图9 为PSO-ZUPT 解算轨迹，实线是作为参考的真实轨迹，点画线为解算轨迹。由于PSO-ZUPT 滤波过程中Qk和Rk是变化的，给出每次PSO 算法中全局最优解的平均值:

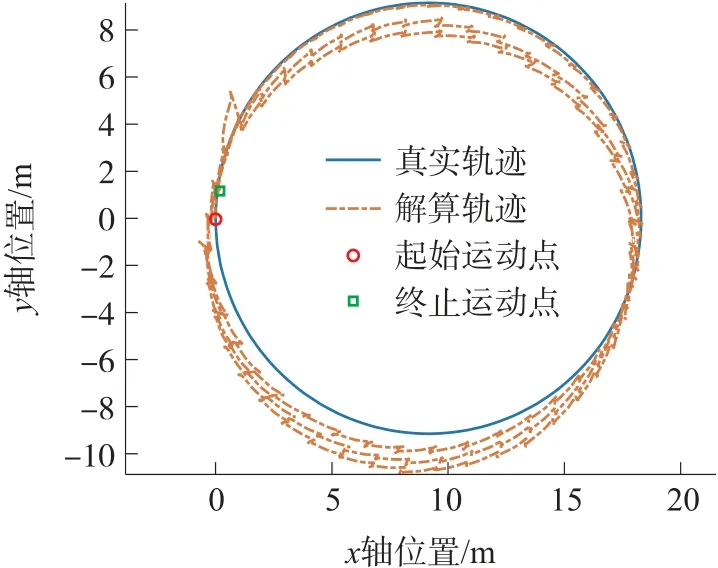
图8 ZUPT 解算轨迹

图9 PSO-ZUPT 解算轨迹

使用标准EKF 需要根据不同测试人员的生物特性、不同惯性器件指标及不同测试环境来确定合适的Qk和Rk，由图8 可见，解算轨迹会出现明显的修正跳变点，且误差较大，轨迹逐渐漂移。PSO 算法可以在EKF 量测过程中对Qk和Rk进行自主寻优，解算轨迹更加平滑，定位精度提高。

为验证算法在长距离行走下的有效性，实验中人员沿400 m 跑道行走并形成闭环路线，采集了行人足部运动的惯导数据，行走轨迹如图10 所示，图中跑道处实线为实际行走轨迹，圆点为起点位置，行人沿实际轨迹行走一圈后回到起点位置。

图10 沿操场跑道的运动轨迹

分别利用ZUPT 和PSO-ZUPT 对跑道数据进行解算，得到的行人运动轨迹如图11 所示。在行人长距离运动的情况下，ZUPT 解算的轨迹与真实轨迹之间的误差明显，本文提出的算法解算的轨迹更接近真实轨迹。经计算，ZUPT 算法解算的轨迹终点位置误差为24.39 m，PSO-ZUPT 算法解算的轨迹终点位置误差为3.02 m，误差减小了87.62%，定位精度有明显提升。

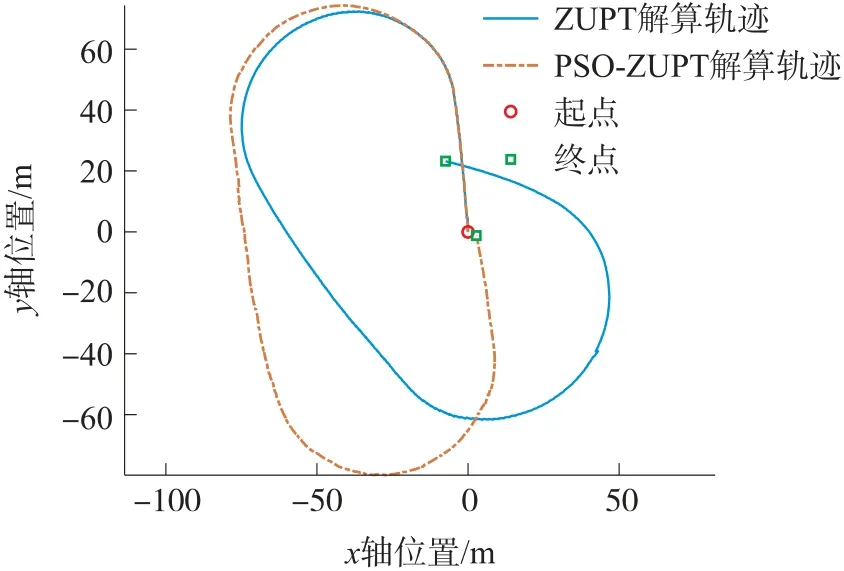
图11 ZUPT 和PSO-ZUPT 解算轨迹对比图

3 总结

本文在研究ZUPT 进行行人自主定位定向的基础上，提出了一种PSO 优化的ZUPT 算法，设计新息序列作为适应度函数，可以调整滤波器的噪声矩阵参数。经多组实验验证，该算法能够有效提高行人零速修正算法解算轨迹的平滑程度，并减小定位误差。在足球场中圈和400 m 跑道的运动轨迹下检验了算法有效性，在足球场中圈行走轨迹的终点位置相对误差为0.25%，在400 m 跑道轨迹的终点位置相对误差为0.76%，结果均优于标准ZUPT 算法，对于行人自主定位定向技术的应用具有一定意义。