双线程滑动窗口多系统GNSS超快精密定轨实现及评估

金炜桐,蔚保国,盛传贞,张京奎,武子谦,陈永昌

(1. 中国电子科技集团公司第五十四研究所,石家庄 050081;2. 卫星导航系统与装备技术国家重点实验室,石家庄 050081)

0 引言

作为位置服务产业全面跨越升级的重要手段,全球导航卫星系统(global navigation satellite system, GNSS)高精度定位在交通、公安及林业等领域已形成规模化应用并全面进入大众市场。随着我国数字经济的高速发展,位置服务产业将升级到以时空服务为核心的综合定位、导航与授时(positioning, navigation and timing, PNT)时空服务产业[1],对GNSS定位的需求也不仅仅局限于高精度,而是迈向“又快(快速收敛)又精(高精度)”定位,因此GNSS提供的时空基准也需要同步响应快速、高精度的GNSS定位需求。

作为GNSS卫星空间基准的信息来源,精密卫星轨道产品是GNSS卫星为用户提供连续精确的PNT服务的先决条件和必要前提[2]。从2000年起,国际GNSS服务组织(international GNSS service, IGS)为满足实时用户需求开始提供超快速轨道产品(IGS ultra-rapid, IGU),后续如武汉大学(Wuhan University, WHU)、欧洲定轨中心(Center for Orbit Determina-tion in Europe, CODE)及德国地学研究中心(Deuts-ches GeoForschungsZentrum, GFZ)等各大分析中心也逐步开始提供相应GNSS超快速轨道产品。由于GNSS卫星在近地空间自由受力(除轨道机动、地影及偏航姿态切换等非平稳运动外),其轨道较为平滑,在较短弧段内进行预报能够维持初始历元的轨道确定精度,因此超快速轨道确定主要基于GNSS基准站的事后观测数据,生成的轨道产品中包含事后观测弧段和预报弧段两部分。相较于滤波法实时定轨[3],目前在同时需要保证精度和稳定性的实时应用中广泛使用的(如实时钟差估计、轨道钟差改正实时数据流生成等)仍是超快精密定轨中的预报部分。IGS官方网站给出了最近60个GPS周期间8个分析中心的超快轨道产品与IGS超快轨道产品的互差量级[4],其中5个分析中心的超快轨道产品与IGS超快轨道产品的互差稳定在5 cm以下,3个分析中心的超快轨道产品与IGS超快轨道产品的互差稳定在5～10 cm。在此期间,各大分析中心提供的超快轨道产品较为稳定,除法国图卢兹空间大地测量团队(Grou-pe de Recherche en Géodésie Spatiale, GRGS)分析中心在GPS 2240～GPS 2242周与IGS超快轨道产品互差超过10 cm外,其他分析中心与IGS超快轨道产品的互差一直保持毫米级别的波动水平。

尽管各大分析中心的GNSS超快速轨道产品目前可在互联网自由获取,但受限于产品自主性需求等因素,仍有必要进行GNSS超快精密定轨的独立实现。本文面向下一代GNSS系统建设,提出了天地协同PNT网络的概念架构,并进行了基础设施、服务中心和自主终端的研发和建设部署,依托天地协同PNT网络服务中心云平台对GNSS四系统卫星进行了超快速定轨,主要贡献如下:介绍了天地协同PNT网络的提出背景、概念内涵以及其服务中心部署的超快速精密定轨软件,给出了服务中心运行的GNSS超快速精密定轨理论模型及算法,以及双线程滑动窗口的精密定轨策略,最后使用重叠弧段比较、与外部分析中心轨道产品比较以及卫星激光测距(satellite laser ranging, SLR)检核3种手段,全面验证了30天的GNSS四系统超快速精密定轨精度。

1 天地协同PNT网络服务中心及超快速精密定轨软件

本文进行的GNSS超快速精密定轨业务部署在天地协同PNT网络服务中心,其中天地协同PNT网络的概念参见文献[5]。服务中心生成的相应轨道产品通过数据接收模块接收的“Multi-GNSS实验”(The Multi-GNSS Experiment, MGEX)测站小时观测数据和广播星历,利用部署在云平台上的超快速精密定轨软件解算得到,所采用的精密定轨软件架构如图1所示。

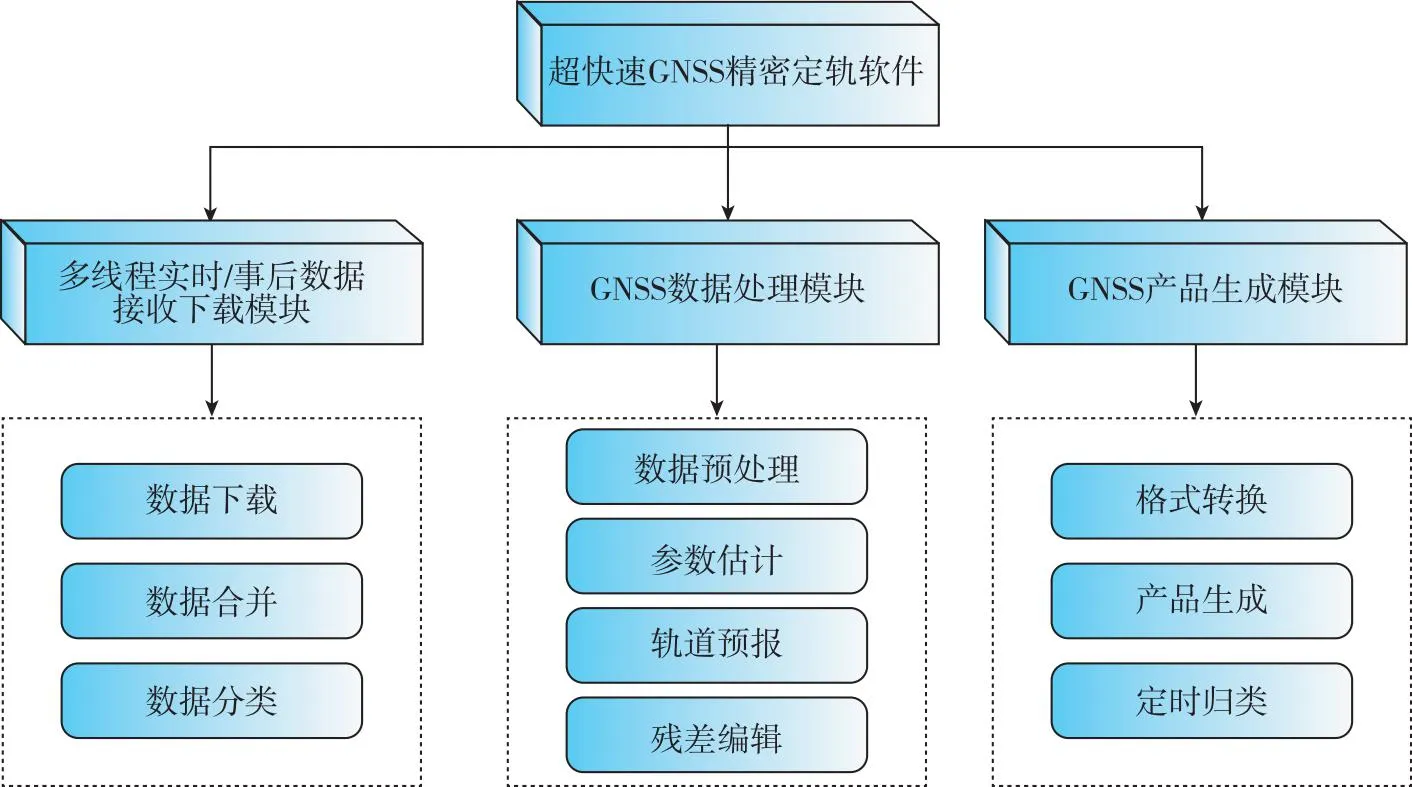
图1 超快速GNSS精密定轨软件架构

超快速GNSS精密定轨软件由三部分核心模块组成。数据接收下载模块采用多线程方式对全球测站的小时观测数据以及小时广播星历进行并行下载,并针对24 h弧段的观测数据和广播星历进行合并存储在相应路径;GNSS数据处理模块首先进行卫星广播星历动力学拟合,观测数据钟跳修复、粗差剔除和周跳探测,然后建立精密定轨法方程,结合最小二乘法对卫星轨道、光压参数及卫星钟差等多类型参数进行联合估计,利用估计后的轨道参数和力模型参数作为初值进行GNSS卫星轨道预报,最后对参数估计中残差较大的观测值进行剔除,该过程迭代进行直至达到最大迭代次数或相应统计指标达到阈值范围内停止迭代;GNSS产品生成模块主要将软件自定义的轨道文件格式转换为标准sp3格式,并按照指定规则命名存储在相应路径。

2 GNSS卫星超快速精密定轨算法及解算策略

2.1 GNSS卫星超快速精密定轨算法及策略

用于GNSS卫星精密定轨的基本观测方程可以表示为

(1)

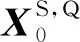
通常采用无电离层组合消除一阶电离层影响,线性化后的误差方程如下

(2)

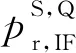
(3)

基于精密定轨基本观测方程和误差方程,本文采用的精密定轨策略如表1所示。

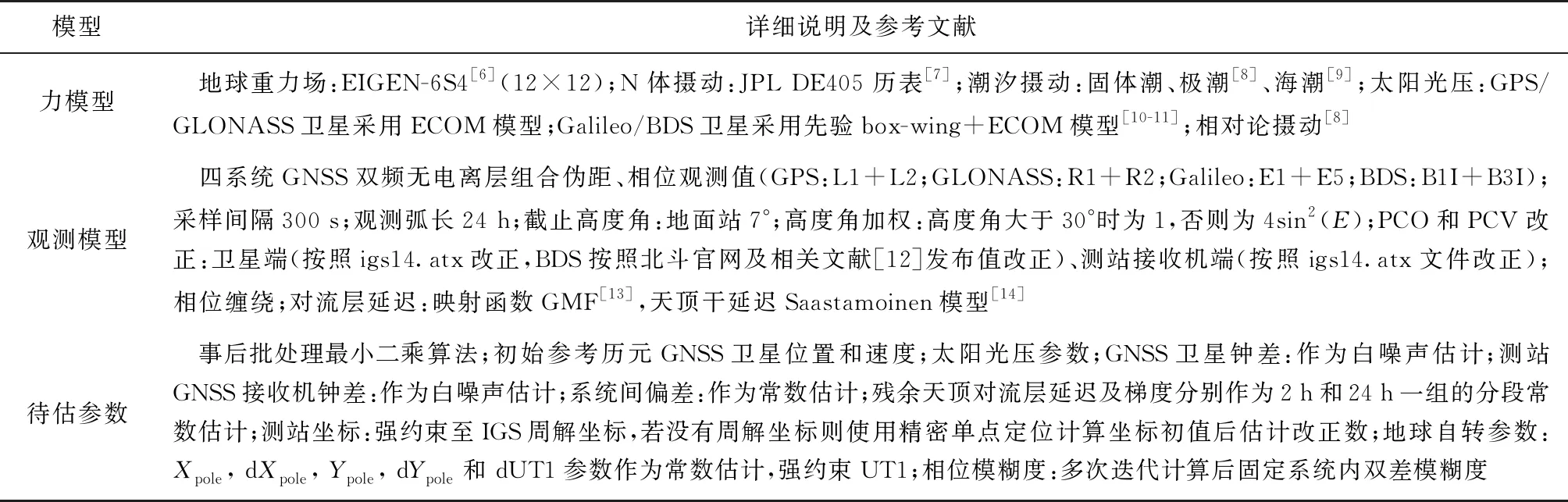
表1 GNSS卫星超快精密定轨模型配置策略

其中Galileo卫星各面板光学参数采用其官网发布的元数据(https://www.gsc-europa.eu/support-to-developers/galileo-satellite-metadata),BDS卫星各面板光学参数参见(http://www.beidou.gov.cn/yw/gfgg/201912/t20191209_19613.html)。钟差基准选取主要有两种方式:一是将卫星钟差对齐到广播星历钟差;另一种是选择外接高精度原子钟的地面测站钟作为基准钟。本文软件采用第二种方式。为避免被选为基准钟的测站没有观测数据的情况发生,在处理策略上选择多个地面测站外接高精度氢原子钟为基准钟候选。确定基准钟的原则为:可用观测值比例(可用观测值数量与观测值总数的比值)大于85%,且可用观测值数量最多。这里可用观测值的具体含义是经过钟跳修复、粗差剔除和周跳探测后实际用于参数估计过程的观测值。

2.2 面向实时服务需求的解算策略

天地协同PNT网络服务中心运行的GNSS超快速精密定轨最终需服务于有实时精密定位需求的用户,因此针对后续的实时估钟和轨道钟差改正数播发等应用,需要部署GNSS超快速精密定轨的运行策略和后台定时任务。目前武汉大学IGS数据中心、地壳动力学数据信息系统(the crustal dynamics data information system, CDDIS)等提供的小时观测数据和各测站广播星历文件滞后约30～45 min,即每天第i(0≤i≤23) h 30～ 45 min期间,分析中心才会完全上传完毕截止到第i(0≤i≤23) h之前的观测数据。在接收数据完毕后,软件运行一次完整定轨流程(指从对数据进行预处理至轨道产品生成完毕)所需时间约1.5 h,图2给出了从2023年年积日151～157天100次完整定轨流程的运行时间统计。

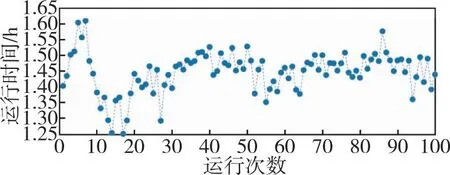
图2 2023年年积日151～157天100次完整定轨流程运行时间统计

从图2中可以看出,一次完整定轨流程的运行时间在1.5 h上下波动(主要由于网络波动以及服务中心其他运行程序的影响),大部分运行时长在1.5 h以内。因此在实际运行一次定轨过程结束后往往还未到第(i+2) h的45 min,仍需等待小时观测数据和广播星历下载完毕才能进行下一次定轨流程,这样一次定轨过程往往会滞后2.75 h。而对于后续实时应用,轨道产品的实际滞后时间更长,这是因为定轨处理流程较为耗时,在这1.5 h内并未有新的轨道生成,所使用的实际仍是上一次定轨得到的轨道产品。为降低后续实时应用所需轨道产品的滞后性,本文采用双线程滑动窗口超快速精密定轨部署策略,具体如下:

1)每个小时的第30 min开启数据下载线程,从武汉大学IGS数据中心和CDDIS下载小时观测数据、各测站广播星历、差分码偏差(differential code bias, DCB)文件,以及测站坐标周解文件和更新地球自转参数(Earth rotation parameters, ERP)文件,具体下载流程如图3所示。

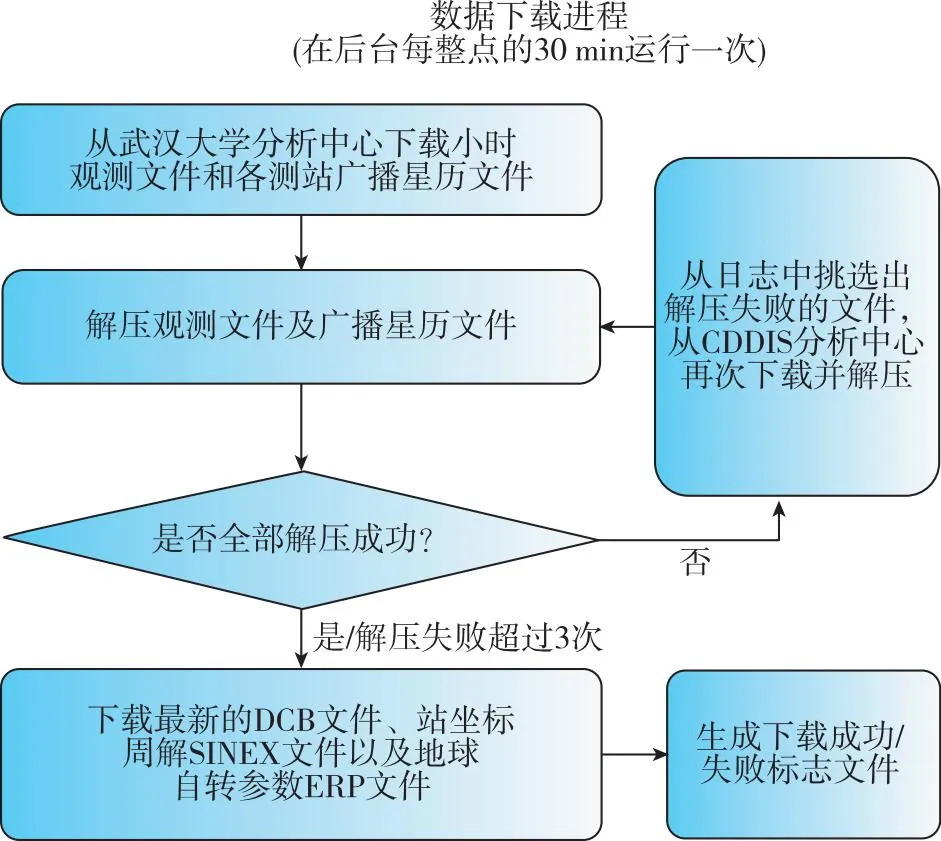
图3 数据下载进程具体算法流程

2)每个奇数小时和偶数小时的第30 min分别开启单独的定轨线程,每个定轨线程的具体流程如图4所示。

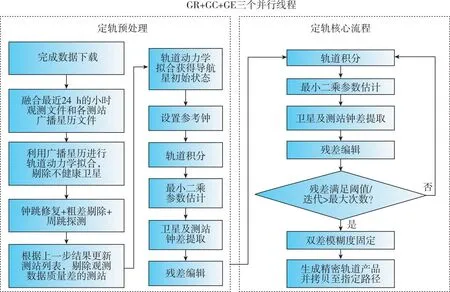
图4 定轨进程具体算法流程

对于下载线程,在下载过程结束后会在指定目录下生成下载成功或失败的标志文件;对于定轨线程,由于网速在实际运行时存在波动现象,该策略在线程的起始处每1 min检测一次下载标志文件是否存在,若超过20 min还未检测到下载成功标志则表示本次数据下载失败,继续进行后续的数据预处理流程。对于数据预处理,首先对各个小时观测文件和各个测站广播星历文件分别进行融合,生成24 h 弧段长度的各测站观测文件和全球广播星历文件;然后将全球广播星历视为观测值对各GNSS卫星进行动力学拟合,剔除不健康卫星;接着对各测站观测数据进行钟跳修复、粗差剔除和周跳探测,根据处理结果剔除数据质量较差的测站,更新测站列表,至此定轨预处理过程完毕。

对于定轨核心进程,本文分GPS+GLONASS(GR)、GPS+Galileo(GE)和GPS+BDS(GC)3个线程并行执行定轨流程,既可以提升定轨整体运行效率,也能够保证在其中一个线程失败时不影响其他线程;最后将3个线程所确定的初始参数进行合并,执行轨道积分,生成精密轨道产品,拷贝到指定产品文件目录。

此外,为了同时满足定轨精度与处理速度要求,从现有的多系统测站中,挑选出了100个测站用于精密定轨。测站选取时,根据纬度将地球表面划分成格网,尽可能保证每个格网点都有用于定轨的测站,并尽量均匀分布,其分布图如图5所示。

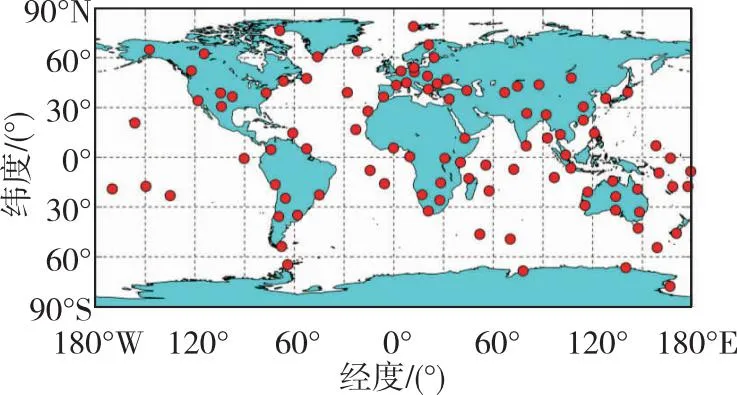
图5 GNSS超快精密定轨测站分布图

3 定轨精度验证及分析

本章采用重叠弧段轨道比较、与外部参考轨道比较和SLR检核3种方式对2023年年积日151～180天的定轨结果进行精度验证。其中重叠弧段轨道比较是指将相邻两次定轨弧段重叠部分的轨道进行比较,是比较轨道内符合精度的常用方式,可验证算法、模型和软件实现的自洽性;与外部参考轨道比较和SLR检核旨在比较轨道的外符合精度,前者是指将同时段定轨结果与分析中心的轨道产品进行比较,本文选择武汉大学分析中心提供的单日最终事后精密轨道产品进行比较;后者则是固定解算的轨道,计算SLR观测量的理论值并将其与SLR实际观测值做差比较[15]。SLR检核对轨道径向偏差较为敏感,目前除GPS卫星外,BDS、GLONASS、Galileo等不同时期的卫星均搭载有SLR反射棱镜,这也为相应的轨道产品SLR检核提供了条件[2]。

进行轨道精度验证的常用指标为所比较的2个轨道序列之差的均方根(root mean square, RMS)误差,具体公式如下

(4)

其中,dRMS表示同时段内2个轨道的三维RMS误差;dA、dC和dR分别表示同时段内2个轨道在沿迹、法向和径向的RMS误差。dA、dC和dR的计算公式具体如下

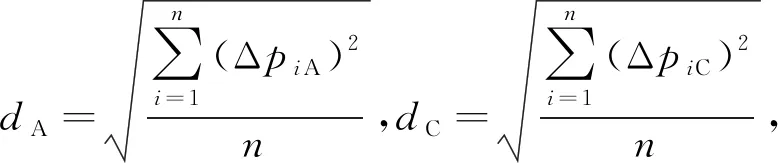
(5)

式中,n表示相同时段内参与轨道比较的历元个数;ΔpiA、ΔpiC和ΔpiR分别表示相同时段内的第i个历元,参与比较的2个轨道在沿迹、法向和径向之差。此外,考虑到本文所用轨道框架与各个分析中心轨道的不一致性,轨道比较时采用了Helmert 7参数转换,以便消除由于框架原点、尺度和旋转所引起的系统性差异[16]。

3.1 重叠弧段轨道比较

本文采用相邻两次的定轨结果进行重叠弧段比较,分事后重叠弧段比较和预报重叠弧段比较两种方式。对于奇数/偶数小时30 min定时运行的定轨线程而言,滑动窗口均为2 h,两种比较方式的示意图如图6所示。

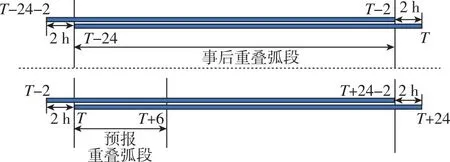
图6 事后和预报重叠弧段示意图

图6中,T-24和T表示某一次生成的轨道产品的初始历元和结束历元。考虑到实时应用不会使用滞后时间过长的超快轨道产品,因此本文选择的预报重叠弧段为6 h。

图7和图8分别显示了2023年年积日151～180天各GNSS卫星事后和预报重叠弧段的平均轨道误差。两图从上到下分别表示GPS卫星、GLONASS卫星、Galileo卫星、BDS2卫星和BDS3卫星,横轴表示卫星PRN号,纵轴表示重叠弧段轨道误差。Along、Cross、Radial和3D-direction分别表示沿迹方向、法向、径向和三维误差。表2给出了GNSS四系统卫星的平均重叠弧段轨道误差统计情况,其中G、R、E以及C2I、C2M和C3M分别表示GPS、GLONASS、Galileo以及BDS2 IGSO、BDS2 MEO以及BDS3 MEO卫星。

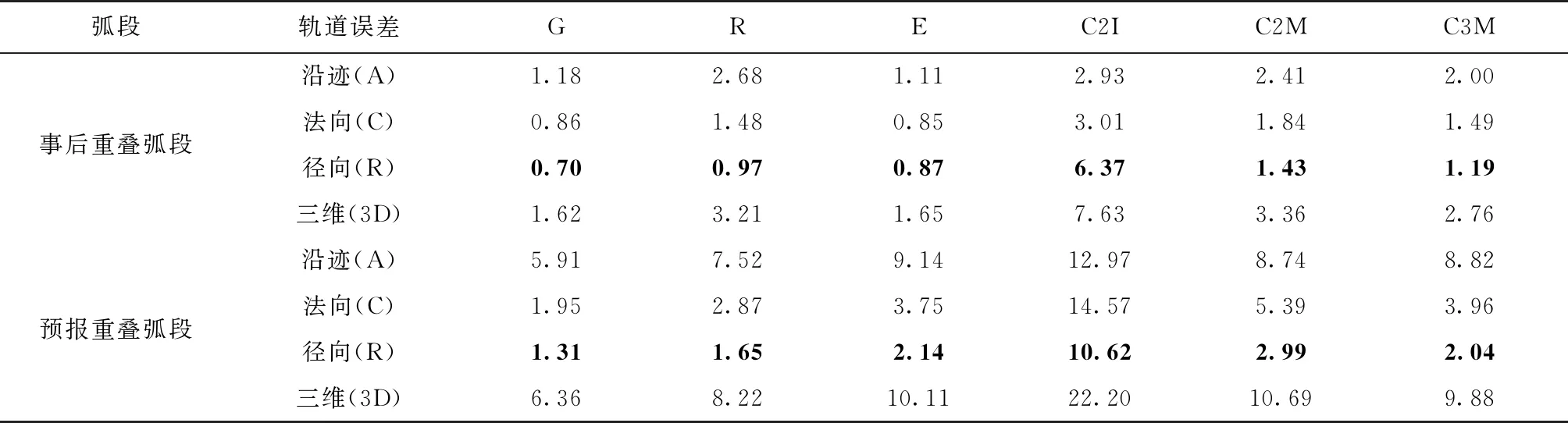
表2 各GNSS卫星平均重叠弧段轨道误差统计表

图7 2023年年积日151～180天各GNSS卫星事后重叠弧段的平均轨道误差

图8 2023年年积日151～180天各GNSS卫星预报重叠弧段的平均轨道误差

对于四系统MEO卫星,无论是事后还是预报重叠弧段,径向轨道误差均稳定在1～3 cm,但预报弧段在沿迹和法向两个方向的轨道误差发散较快,导致预报重叠弧段的三维轨道误差大于事后重叠弧段。其中事后重叠弧段的四系统MEO卫星三维轨道误差稳定在2～3 cm,预报重叠弧段的四系统MEO卫星三维轨道误差则稳定在8～10 cm。BDS2 IGSO卫星观测几何不同于MEO卫星,其整体重叠弧段轨道误差相比于MEO卫星较大:其事后和预报重叠弧段一维轨道误差最小的方向分别约为3 cm和11 cm,三维轨道误差分别约为6 cm和22 cm。

3.2 与外部参考轨道比较

本节选择将定轨结果与武汉大学分析中心的最终事后精密轨道产品对比。图9和图10分别显示了2023年年积日151～180天各GNSS卫星的事后和预报弧段与同时段分析中心轨道产品对比的平均轨道误差。两图从上到下分别表示GPS卫星、GLONASS卫星、Galileo卫星、BDS2卫星和BDS3卫星,横轴表示卫星PRN号,纵轴表示重叠弧段轨道误差。Along、Cross、Radial和3D-direction分别表示沿迹方向、法向、径向和三维误差。表3给出了GNSS四系统卫星的平均重叠弧段轨道误差统计情况,其中G、R、E以及C2I、C2M和C3M分别表示GPS、GLONASS、Galileo和BDS2 IGSO、BDS2 MEO以及BDS3 MEO卫星。

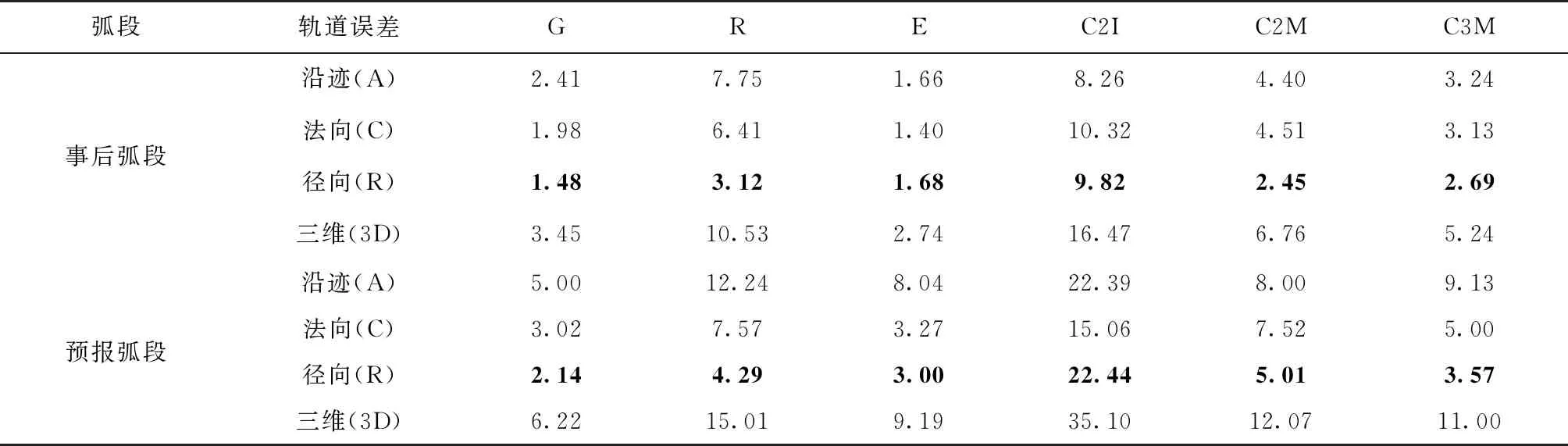
表3 各GNSS卫星与外部轨道产品对比轨道误差统计表

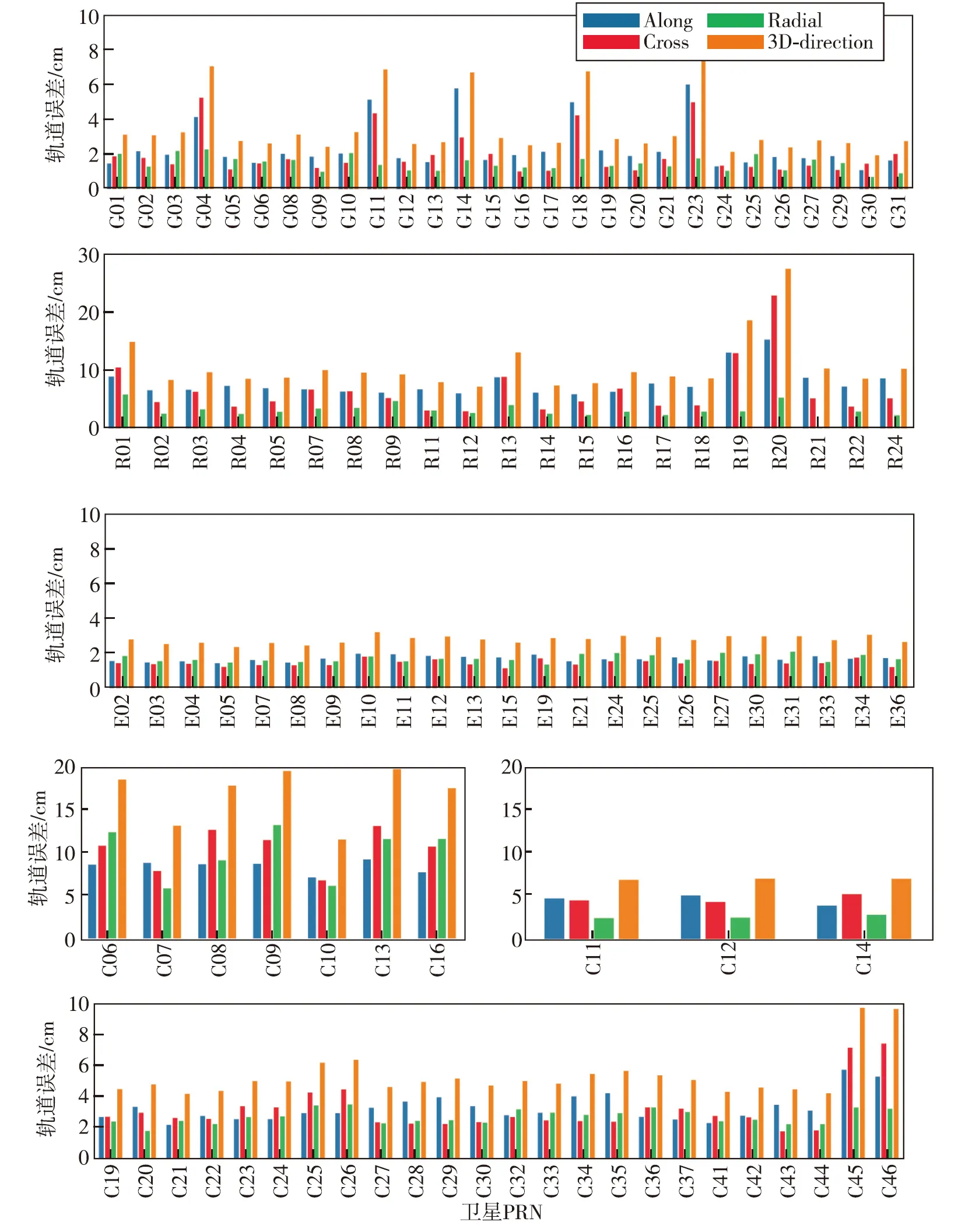
图9 2023年年积日151～180天各GNSS卫星与外部轨道产品比较的事后弧段平均轨道误差

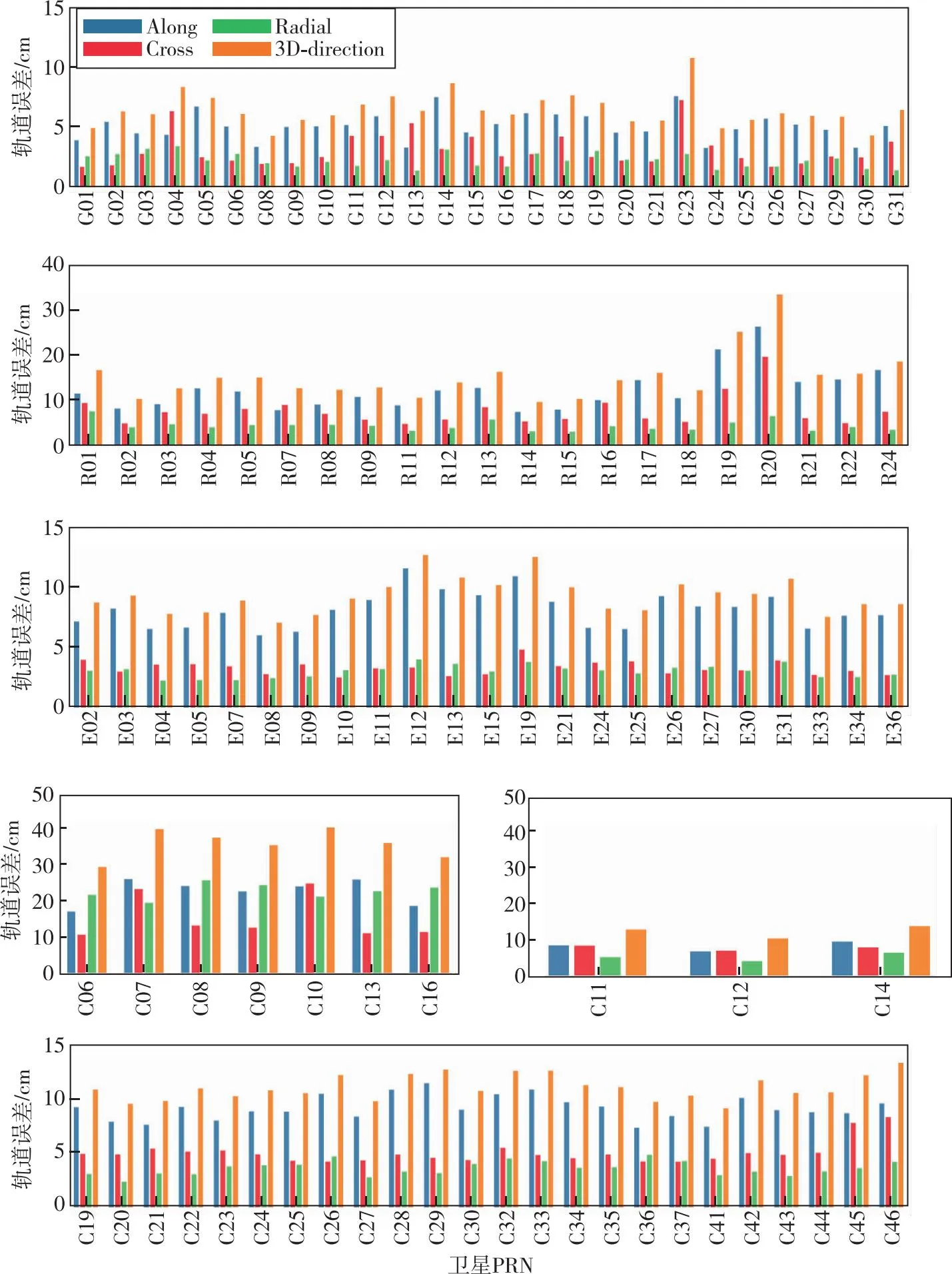
图10 2023年年积日151～180天各GNSS卫星与外部轨道产品比较的预报弧段平均轨道误差

可以看出,当与外部轨道产品进行比较时,各系统GNSS卫星的整体定轨精度较重叠弧段方式略低。对于事后弧段,GPS和Galileo卫星与外部轨道产品对比的径向平均轨道误差最小,稳定在1～2 cm之间;三维轨道误差也整体最小,稳定在3～4 cm之间。特别地,G04、G11、G14、G18和G23这几颗BLOCK IIIA卫星沿迹方向轨道误差较其他卫星量级略大,这是因为两者采用的光压模型和相应轨道参数估计策略方式不同。武汉大学分析中心的轨道产品针对GPS BLOCK IIIA卫星采用7参数ECOM模型,在参数估计方面引入了沿迹方向的常数参数吸收误差,而GPS III卫星的箱体是长方体,传统的5参数ECOM光压模型适用程度低。其他分析中心的轨道产品也采用了较新光压模型和相应的经验加速度参数估计策略,如CODE和GFZ均采用7参数模型,且在沿迹、法向和径向3个方向引入了伪随机参数并加入先验约束,本软件后续将针对光压模型和经验加速度估计方面进行升级改进。GLONASS卫星的平均径向轨道误差稳定在3～4 cm之间,但沿迹和法向轨道误差均在6～8 cm之间,导致整体的平均轨道误差达到10 cm左右量级;BDS2 MEO和BDS3 MEO卫星平均径向轨道误差均稳定在2～3 cm之间,三维轨道误差整体稳定在5～7 cm水平。BDS2 IGSO卫星观测构型不同于MEO卫星,其一维最小轨道误差整体稳定在8～9 cm 之间,三维轨道误差位于15～18 cm量级。

对于预报弧段,四系统MEO卫星的径向平均轨道误差相比于事后弧段增加了约1～2 cm量级。其中GPS和Galileo卫星与外部轨道产品对比的径向平均轨道误差稳定在2～3 cm之间,GLONASS卫星与外部轨道产品对比的径向平均轨道误差稳定在4～5 cm 之间,BDS2 MEO和BDS3 MEO卫星径向平均轨道误差均稳定在3～5 cm之间。但轨道预报在沿迹和法向发散较快,导致三维轨道误差量级增大。其中GPS卫星三维轨道误差最小,稳定在6～7 cm水平;Galileo卫星次之,其整体三维轨道误差稳定在9 cm 水平;GLONASS、BDS2 MEO和BDS MEO卫星的整体平均三维轨道误差则稳定在10～15 cm水平。BDS2 IGSO卫星观测构型不同于MEO卫星,其预报弧段的一维最小轨道误差整体稳定在15 cm水平,三维轨道误差位于35 cm水平。

3.3 SLR检核

本节对2023年年积日151～180天的超快定轨结果利用事后弧段和预报弧段两种方式进行SLR残差检核,事后弧段和预报弧段的长度分别为24 h和6 h。在进行SLR检核时,若残差大于50 cm则被视为粗差加以剔除[17]。为保证预报弧段能够覆盖当天所有SLR观测值,所参与计算的轨道在当天滑动窗口生成的所有轨道产品中进行了遍历,直至能够覆盖当天所有SLR观测值为止。在2023年年积日151～180天期间内,仅BDS和Galileo系统可以下载SLR观测值,因此本节仅对这两个系统的卫星进行SLR检核。图11和图12分别显示了事后弧段Galileo和BDS卫星的SLR残差。其中为防止在一张图中表示所有Galileo卫星造成混淆,分为了6个子图进行展示。图12中左侧和右侧分别表示BDS2和BDS3卫星的SLR检核残差。两图的横轴表示时间,纵轴表示SLR残差量级。图13和图14分别显示了预报弧段Galileo和BDS卫星的SLR残差,两图的具体排布与图11和图12相同,横轴表示时间,纵轴表示SLR残差量级。表4给出了事后弧段和预报弧段Galileo和BDS卫星的SLR残差统计,表中均值和标准差均针对弧段内各自系统内所有卫星进行统计。

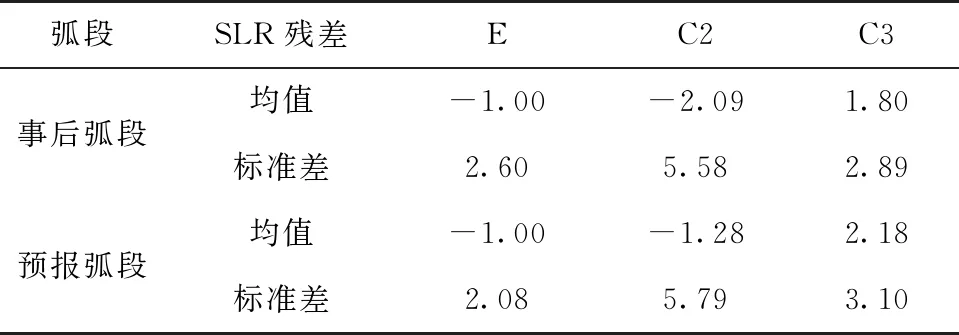
表4 BDS和Galileo卫星平均SLR残差统计表

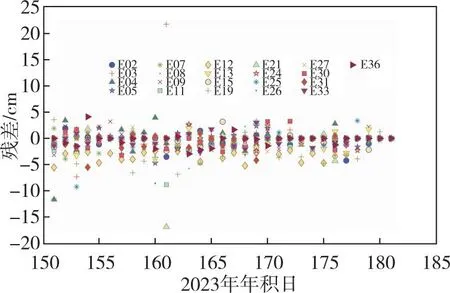
图11 事后弧段2023年年积日151～180天Galileo卫星SLR检核残差

图12 事后弧段2023年年积日151～180天BDS卫星SLR检核残差

图13 预报弧段2023年年积日151～180天Galileo卫星SLR检核残差

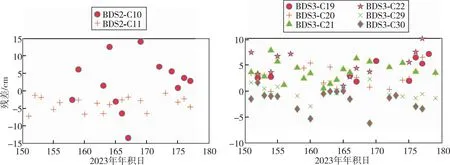
图14 预报弧段2023年年积日151～180天BDS卫星SLR检核残差

由于SLR检核对轨道径向误差更敏感,鉴于轨道预报在径向的发散程度不大,因此事后弧段和预报弧段的SLR残差量级基本一致。其中,Galileo卫星SLR残差均值稳定在1 cm水平,标准差稳定在2～3 cm水平;BDS卫星SLR残差均值基本稳定在1～3 cm量级,标准差稳定在3～6 cm水平。

4 结论

本文基于天地协同PNT网络服务中心云平台实现了GNSS四系统超快速精密定轨,并对定轨结果进行了精度评价,介绍了天地协同PNT网络概念内涵及服务中心超快速精密定轨软件架构,提出了一种双线程滑动窗口的超快速精密定轨策略,利用重叠弧段比较、与外部轨道产品比较以及SLR检核3种方式对2023年年积日151～180天的超快精密定轨结果进行统计分析,得出如下结论:

1)对于轨道内符合精度,GPS、GLONASS、Galileo卫星以及BDS2和BDS3 MEO卫星事后和预报重叠弧段径向轨道RMS误差均稳定在1～3 cm,事后重叠弧段三维轨道RMS误差稳定在2～3 cm,预报重叠弧段三维轨道RMS误差稳定在8～10 cm;BDS2 IGSO卫星事后和预报重叠弧段最小一维轨道RMS误差基本稳定在3～6 cm,三维轨道误差分别为11 cm和22 cm水平。

2)对于轨道外符合精度,与武汉大学分析中心的最终事后精密轨道产品相比,GPS、GLONASS、Galileo卫星以及BDS2和BDS3 MEO卫星在事后弧段和预报弧段的径向轨道RMS误差整体在2～5 cm水平。GPS卫星三维轨道误差最小,Galileo次之,然后依次是BDS3 MEO、BDS2 MEO和GLONASS卫星。BDS2 IGSO卫星观测构型与MEO卫星不同,其轨道误差大于MEO卫星;Galileo卫星SLR残差均值稳定在1 cm水平,标准差稳定在2～3 cm水平;BDS卫星SLR残差均值基本稳定在1～3 cm量级,标准差稳定在3～6 cm水平。

3)无论事后弧段还是预报弧段、进行轨道内符合还是外符合精度统计,MEO卫星沿迹和法向轨道误差相对于径向发散较快,其中径向轨道误差稳定在2～5 cm水平,能够满足后续厘米级实时定位应用对空间基准的精度需求。