HOI延迟对LEO卫星简化动力学POD的影响

张兵良,方 卓,李珊珊,曾 彬

(1.南京农业大学公共管理学院,南京 210095;2.南京数维测绘有限公司,南京 211808;3.南京信息工程大学测绘与遥感学院,南京 210044)

0 引言

自搭载星载全球定位系统(global positioning system,GPS)接收机的TOPEX/Poseidon的定轨精度达到厘米级以来[1],使用星载全球导航卫星系统(global navigation satellite system,GNSS)数据的精密定轨(precise orbit determination,POD)技术已广泛应用于低地球轨道(low Earth orbit,LEO)卫星,具有全天候、实时、连续和高精度观测的特点。后续的LEO卫星中,使用GNSS数据的POD精度也达到了厘米级[2]。Kang等[3]使用GRACE的GPS数据进行POD,结果表明,轨道的三维精度约为2 cm。Ijssel等[4]使用SWARM的GPS数据进行POD,并通过卫星激光测距(satellite laser ranging,SLR)检核定轨精度。结果表明,动态轨道的精度约为4 cm,简化动力学(reduced-dynamic,RD)轨道的三维精度约为2.5 cm。 Casotto等[5]使用GOCE的GPS数据进行POD,结果表明,轨道的三维精度约为6 cm。电离层延迟对LEO卫星的POD是不可避免的误差源,通常使用无电离层(ionospheric-free,IF)线性组合(linear combination,LC)消除一阶电离层延迟,但不能消除高阶电离层(high-order ionospheric,HOI)[6-7]延迟。HOI延迟的存在会导致电离层密度的变化,这种变化会对卫星的轨道产生扰动,使其偏离预定的轨道,这意味着卫星可能无法准确地达到所需的位置或保持稳定的轨道;HOI延迟对卫星通信也具有重要影响,电离层中的电离气体会对无线信号传输产生衰减和散射,这意味着卫星与地面站之间的通信可能会受到干扰或中断,从而影响定位和轨道控制;HOI还可能引起卫星的电磁干扰,当卫星穿越电离层时,它会与电离气体发生相互作用,产生电磁辐射,这种辐射可能会干扰其他卫星或地面设备的正常运行,从而影响精密定位和轨道控制的精度。简而言之,HOI延迟对精密卫星定轨达到毫米至亚毫米级别的精度具有重要影响。了解这些影响并采取适当的措施可以更好地实现精密定位和轨道控制,从而更准确地了解地球和其他天体的运动。

HOI延迟主要包括两个部分:法拉第旋转效应引起的二阶电离层延迟和电离层射线折射效应引起的三阶电离层延迟。Petrie等[8]研究了电离层的相关特性,结果表明,HOI延迟影响微乎其微。Cai等[9]使用了不同地区和时间的GNSS数据研究了HOI延迟影响。结果表明,HOI延迟对GNSS接收机观测的影响达到厘米级。Liu等[10]实验表明HOI延迟对精密单点定位(precise point positioning,PPP)的影响达到毫米级。方卓等[11]研究表明HOI延迟对对流层参数估计的影响达到厘米级。然而,由于LEO卫星位置的特殊性,计算地面GNSS接收机的HOI延迟的方法不再适用。

随着技术的发展和扰动力模型的不断完善,使用星载GNSS数据进行简化动力学POD的精度逐渐达到毫米级水平,此时HOI延迟成为需要考虑的误差项。Qi等[12]证明了HOI延迟对GRACE-FO卫星的POD的影响大约在亚毫米级别,但该研究存在以下不足。一方面,使用经验模型计算电离层等效高度,未考虑不同电离层环境的自由电子分布;另一方面,使用伪距来计算斜路径总电子含量(slant total electron content,STEC),因此得到的STEC不准确;最后,Qi等[12]仅讨论了HOI延迟对LEO卫星简化动力学POD的影响,但未考虑HOI延迟对LEO卫星不同轨道高度POD的影响。

基于此,本文改进了LEO卫星HOI延迟的计算模型,使用双频GNSS接收机观测值,采用Montenbruck等[13]提出的积分方法计算等效薄层高度,并利用平滑伪距观测值计算STEC。分析和讨论了GOCE、GRACE-A和SWARM-A/B 4颗LEO卫星不同轨道高度HOI延迟的变化幅度。

1 算法原理

1.1 STEC算法原理

通常使用全球电离层地图(global ionospheric map,GIM)数据计算HOI延迟对地面GNSS接收机观测的影响。由于LEO和GNSS卫星间的轨道高度不同,两者之间的空间并不包含整个电离层。因此,这种方法不再适用,需要探索一种新的计算模型,重新校准电离层等效高度并正确计算STEC显得尤为重要。

信号传播路径上的总电子含量(total electron content,TEC)通常被压缩到一个特定高度上的无限薄层中,以简化电子含量的积分计算[14-15]。薄层的高度即为电离层的等效高度,并且利用薄层直接研究和模拟电离层中电子的水平分布。电离层中的自由电子分布在此高度上下大体相同。通常情况下,电离层建模的等效薄层高度约为300～450 km。

通过积分方法可以计算不同LEO卫星电离层等效高度。根据电离层等效高度的定义,当LEO卫星轨道和某一高度间的电子含量占LEO卫星轨道上方TEC的50%时,该高度可以视为电离层的等效高度。LEO卫星轨道上方的电子含量通过Chapman提出的电子密度分布函数积分计算得到,可以表示为[16]

(1)

式中,zIP=(hIP-h0)/H,zs=(hs-h0)/H。式(1)也可以表示为

(2)

式中,hIP和hs分别表示LEO卫星电离层等效高度和轨道高度;h0表示电子密度峰值的高度;H表示高程。

为了减小误差并获得高精度的STEC,需要使用载波相位观测方法对星载GPS数据平滑伪距,可以表示为[17]

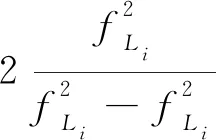
(ΦL2(t)-ΦL2(t-1))

(3)

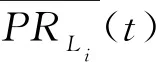
DCBr+εL1L2

(4)

式中,ρ表示GPS卫星到LEO卫星GNSS接收机的几何距离;DCBs和DCBr分别表示GPS卫星和LEO卫星GNSS接收机的差分码偏差(即两个频率间的硬件延迟);εL1L2表示未建模的残差效应。

电离层延迟也可以表示为[13]

c(DCBs+DCBr)]

(5)

式中,c表示光在真空中的传播速度。硬件延迟是由卫星到接收机的信号在硬件路径和内部电子回路传播过程中产生的偏差,这种偏差无法完全一致,并且会随温度和时间等因素而变化[18-20]。Yuan等[21]实验结果表明了硬件延迟在一天内变化很小。为了简化计算,GPS卫星和LEO卫星GNSS接收器的硬件延迟每天被视为固定值,可以从TEC相关的产品中直接获得卫星的差分码偏差(differential code bias,DCB)。

1.2 HOI延迟算法原理

电磁波信号在电离层中的传播速度和折射率可以表示为

(6)

式中,n表示折射率。根据Appleton-Hartree简化方程[8],可以得到折射率。通过式(6)可以计算LEO卫星载波信号传播的速度,对速度积分即可得到GPS卫星到LEO卫星GNSS接收机的几何距离[22]。电离层伪距观测和载波相位观测方程可以表示为

(7)

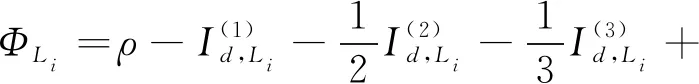
(8)

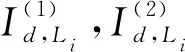
(9)

(10)

式中,e=1.602 18×10-19表示库伦电子;me=9.109 39×10-31表示电子质量;ε=8.854 2×10-12表示真空介电常数;B表示电离层穿刺点(ionospheric pierce point,IPP)地磁场强度;θ表示电磁波信号传播方向与地磁场间的夹角;η=0.66表示函数因子[24];Ne,max表示电子峰值密度,可以表示为

(11)

式(11)是一个经验公式,它是Fritsche等[25]提出的Ne,max作为TEC函数的线性插值。

2 算例分析

为了探讨HOI延迟对LEO卫星不同轨道高度简化动力学POD精度的影响,一方面需要选择合理的LEO卫星观测和实验时间;另一方面,正确计算HOI延迟需要合理的处理策略。本文选择GOCE、GRACE-A和SWARM-A/B 4颗LEO卫星作为实验对象,研究和分析了HOI延迟对LEO卫星不同轨道高度简化动力学POD精度的影响。表1列出了GOCE、GRACE-A和SWARM-A/B 4颗LEO卫星的轨道高度、轨道倾角、发射日期等基本信息。

表1 LEO卫星基本信息

通过表1可知,GOCE,GRACE-A,SWARM-A/B 4颗卫星分别分布在轨道高度为200～500 km范围内。电离层活动规律大致相同,图1显示了利用国际参考电离层-2016(international reference ionosphere-2016,IRI-2016)模型计算获得电子密度分布随高度变化的曲线图。通过积分电子密度方法,即可获得不同高度的自由电子含量。分析图1可知,高度大于500 km时,电子含量仅占电离层TEC的极小部分。电离层活动与太阳活动水平状态密切相关,可以用F10.7指数[26]表示太阳活动水平状态。为了减少太阳活动水平对电离层活动造成的影响,本文选择太阳活动水平状态大致相同的两个时期作为研究对象。

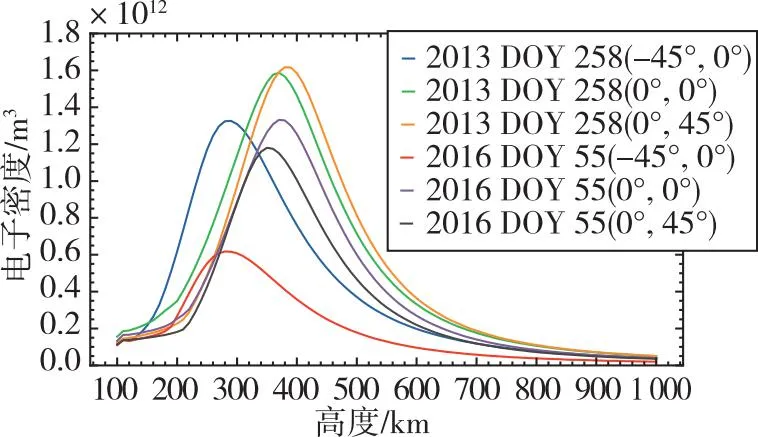
图1 电子密度分布图

2.1 处理策略

首先,利用平滑伪距的方法处理LEO卫星的原始观测数据,分别计算每组观测对应的STEC值。其次,分别利用IRI-2016模型和电子密度积分方法获得电离层F2层和等效薄层的高度。然后,结合GPS精密星历和LEO精密科学轨道(precision science orbit,PSO)数据,利用第13代国际地磁参考场(international geomagnetic reference field: the 13thgeneration,IGRF-13)模型获得IPP位置的地磁场强度和方向,并计算GPS信号传播方向与IPP位置的地磁场夹角。利用式(9)、式(10)和式(11),获得电离层延迟二阶和三阶项。剔除截止高度角小于15°、观测段长度少于10个历元以及每个观测段末尾的数据。最后,分析了HOI延迟对LEO卫星重叠轨道、PSO比较和SLR检核结果的影响。

2.2 LEO卫星不同轨道高度HOI延迟特点

已往研究表明,F10.7指数、DST指数和F2层高度是反映电离层活动的主要指标[27]。为了减少电离层和地磁场变化对HOI延迟产生的影响,实验选择了2012年DOY 251和2016 年DOY 44的观测数据进行处理,计算获得两天的HOI延迟平均值(Mean)。分析表2可知,电离层延迟三阶项对GPS信号影响较小,仅约占HOI延迟的5%。HOI延迟对GPS L1载波信号的影响约占L2载波信号的50%。随着LEO卫星轨道高度的增加,HOI延迟逐渐减小。HOI延迟平均值对最低轨道高度GOCE卫星和最高轨道高度SWARM-B卫星影响最大分别达到7 mm和2 mm。

图2显示了HOI延迟随LEO卫星不同轨道高度变化的折线图。随着LEO卫星轨道高度的增加,HOI延迟呈现迅速下降,然后逐渐趋于平缓的趋势。分析图2可知,2016年DOY 44电离层F2层的带电离子主要集中在约338 km的轨道高度。绝大部分带电离子位于GOCE和GRACE-A卫星轨道高度之间,HOI延迟随轨道高度变化趋势较大。当轨道高度超过电离层F2层后,电离层的电子密度在500 km高度呈现迅速下降,然后逐渐趋于平缓的趋势,这与HOI延迟随LEO卫星不同轨道高度变化趋势相近。

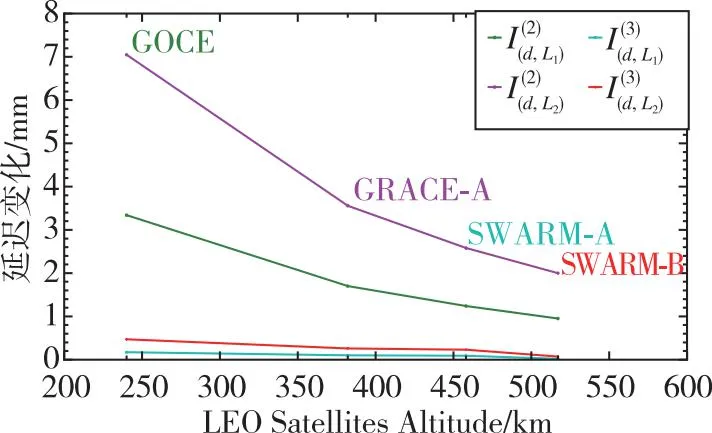
图2 HOI延迟随LEO卫星高度变化折线图

2.3 HOI延迟对LEO卫星不同轨道高度简化动力学POD精度的影响

为了研究HOI延迟对LEO卫星不同轨道高度简化动力学POD精度的影响,本文处理了2013年DOY(244～253)GOCE卫星的GPS数据和2016年 DOY(41～50)GRACE-A,SWARM-A/B的GPS数据(如表1所示)。计算获得4颗LEO卫星的HOI延迟,因此,LEO卫星原始GPS观测值校正可以表示为

(12)

(13)

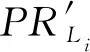
通过BERNESE 5.2软件对HOI延迟校正前后的两组GPS观测数据进行了简化动力学POD处理。其中,处理阶段设置截止高度角为5°,采样间隔为10 s,电离层延迟使用IF LC组合。本文通过重叠轨道分析比较两个轨道内部符合精度,PSO比较和SLR检核分析两个轨道外部符合精度。

通过卫星轨道RTN(radial tangential normal)坐标系分析简化动力学POD精度。其中,RTN坐标系的原点是卫星的质心。R表示径向,从地球中心到卫星质心的径向;T表示切向,垂直于轨道平面R轴,并指向卫星运动的方向;N表示法向,与R和T形成一个右手坐标系。

2.4 重叠轨道分析

LEO卫星的GPS观测数据被分为两个时段进行POD,分别为0～18 h和12～24 h。重叠时间段为12～18 h,总计6 h。图3和图4展示了HOI延迟校正前后的4颗LEO卫星的重叠轨道(overlapping orbit)分析结果。通过HOI延迟校正后,重叠轨道并未出现较大偏差,这表明本文选择的简化动力学POD策略和模型是合适的。HOI延迟校正后的R、T、N和3D方向的重叠轨道分析数值均小于忽略HOI延迟,这表明HOI延迟校正可以提高LEO卫星简化动力学POD内部符合精度。随着LEO卫星轨道高度的增加,差值减小,其变化趋势与HOI延迟随高度变化趋势相近。

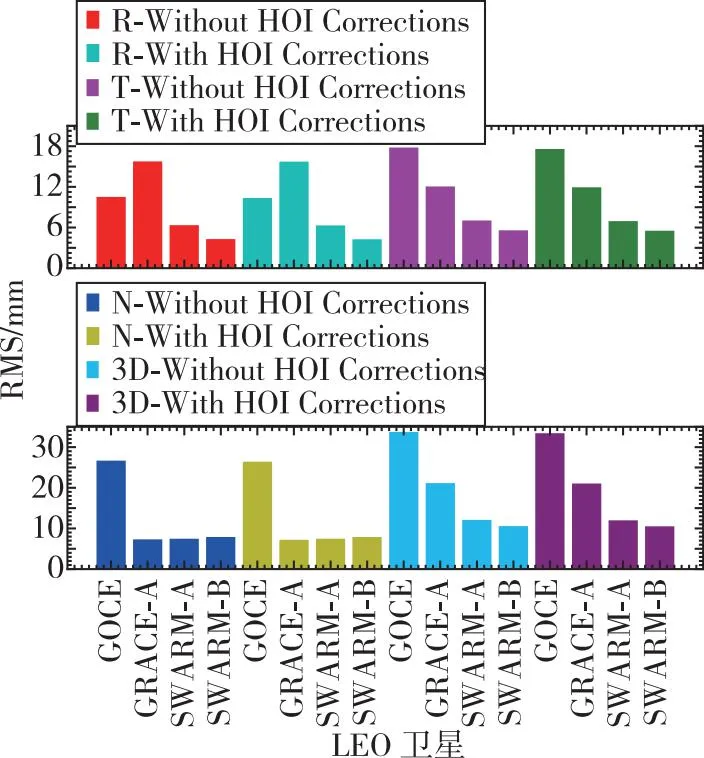
图3 HOI延迟校正前后多天重叠轨道分析RMS

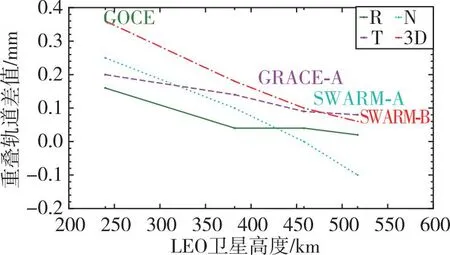
图4 HOI延迟校正前后多天重叠轨道分析RMS差值

2.5 PSO比较

通过BERNESE 5.2软件分别对HOI延迟校正前后4颗LEO卫星的两组GPS观测数据进行简化动力学POD处理,并与官方的PSOs进行比较。图5和图6展示了两个轨道多天RMS平均值PSO的比较结果。HOI延迟产生的影响具体表现为原始轨道和校正后轨道之间的PSO验证结果差值。

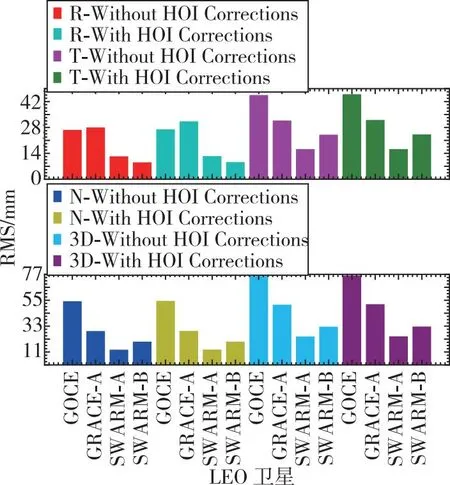
图5 HOI延迟校正前后多天PSO比较RMS平均值

图6 HOI延迟校正前后多天PSO比较RMS平均值差值

分析图5可知,4颗LEO卫星简化动力学POD精度可以达到厘米级,这表明在POD中使用的简化动力学POD策略对这4颗LEO卫星是可行的。由于官方机构在计算LEO卫星轨道时仅使用LC来消除一阶电离层延迟,忽略HOI延迟对简化动力学POD精度的影响,因此HOI延迟校正后的PSO验证结果较差。此外,随着LEO卫星轨道高度的增加,HOI延迟校正前后的轨道差值的绝对值减小,但减小趋势与先前计算得到的HOI延迟与卫星轨道高度的变化趋势不同。这是因为HOI延迟对LEO卫星简化动力学POD精度的提升较小。

2.6 SLR检核

目前,SLR验证是轨道验证最准确的方法[2],因此,更适用于验证HOI延迟对LEO卫星不同轨道高度简化动力学POD精度的影响。通过BERNESE 5.2软件分别对2012年DOY(244～253)GOCE卫星以及2016年DOY(41～50)GRACE-A和SWARM-A/B卫星HOI延迟校正前后的两组GPS观测数据简化动力学POD结果进行SLR检核。在数据处理过程中,设置卫星高度截止角为7°,使用MENDES-PAVLIS经验模型校正对流层延迟。分别与99,138,582和2019个Normal Point(NP)数据集相关联的GOCE、GRACE-A和SWARM-A/B卫星。使用BERNESE 5.2软件计算单日每个SLR站点的检查残差的RMS。剔除单日NP数量少于5个的站点或者检查残差RMS不符合三倍中位数误差准则的数据集。10天时间段剔除4颗LEO卫星的9,8,14和18个NP数据集占卫星总数据的比例分别为9%,6%,3%和1%。在删除数据后,将NP数量为权重的所有SLR站点的RMS加权平均值视为同一天的SLR检查结果,可获得4颗LEO卫星两个轨道多天SLR检核结果RMS平均值,如图7所示。RMS平均值差值表示两个轨道的SLR检查结果比较差值。在考虑HOI延迟后,4颗卫星的SLR检查值均有所下降,显示出考虑HOI延迟可以提高LEO卫星简化动力学POD精度。两个轨道之间的差值随着LEO卫星轨道高度的增加而逐渐减小,减小趋势与HOI延迟随LEO卫星轨道高度变化的重叠轨道的趋势相同。

图7 HOI校正前后多天SLR检核结果

3 结论

本文改进了LEO卫星HOI延迟计算方法。首先,利用GOCE、GRACE-A和SWARM-A/B 4颗LEO卫星分析了HOI延迟对LEO卫星不同轨道高度简化动力学POD精度的影响,得出的主要结论如下:

1)当地磁场和电离层活动相近时,三阶电离层延迟对LEO卫星平均影响小于0.5 mm,约占HOI总延迟的5%,因此,对于轨道高度较高的LEO卫星,可以忽略三阶电离层延迟的影响。

2)二阶电离层延迟对LEO卫星简化动力学POD精度的影响达到毫米级。HOI延迟随LEO卫星轨道高度变化趋势与基于IRI-2016模型获得的电子密度随高度变化趋势一致。轨道越高,HOI延迟越低,具体表现为250～500 km范围内(包含F2层)迅速下降,然后逐渐趋于平稳趋势。

3)重叠轨道分析表明:HOI延迟可以提高LEO卫星简化动力学POD内符合精度。随着轨道高度的增加,改进效果逐渐减小,变化趋势与HOI延迟随高度变化相似。SLR检核结果表明:HOI延迟校正后,LEO卫星不同轨道高度简化动力学POD精度得到了提高,随着轨道高度的增加,轨道精度变化逐渐减小。然而,PSO比较结果出现了反常,这是因为官方机构在计算LEO卫星轨道时仅使用IF LC消除一阶电离层延迟,忽略了HOI延迟对简化动力学POD精度的影响。随着轨道高度的增加,两个轨道PSO比较结果之间的差值逐渐减小。HOI延迟校正对GOCE、GRACE-A和SWARM-A/B 4颗卫星POD精度分别提高了0.92,0.22,0.21和0.18 mm。