基于半静态调度与资源竞争的uRLLC业务时延分析

高月红，王小琦，洪 霄，宁 智，贺 佳

(北京邮电大学 信息与通信工程学院，北京 100876)

0 引言

随着无线通信技术与计算机网络的飞速发展,无线网络上承载的业务从单一话音业务转变成包含文本、语音、图像和视频等信息的综合业务流[1]。不同种类的业务流,对网络服务质量(Quality of Service,QoS)保障的要求往往不同[2]。特别是一些新兴的时延敏感业务,对网络时延、吞吐量、丢包率和抖动等提出了极高的要求。例如,工业控制系统、无人驾驶和交互式远程医疗等需要将端到端时延控制在μs至ms级,将时延抖动控制在μs级,将可靠性控制在99.999%以上[3]。本文重点关注超可靠低时延通信(ultra Reliable and Low Latency Communication,uRLLC)业务,并研究其在无线通信系统上行链路的时延保障结果问题。uRLLC是第五代移动通信(5th-Generation,5G)中的一个重要应用场景,其对时延与可靠性的要求较为严苛[4],相较于5G,另一大应用场景增强型移动宽带(Enhance Mobile Broadband,eMBB)业务具有更高的优先级[5]。uRLLC被认为是工业自动化、智能交通和远程医疗等众多新兴领域的技术基础,能够提供可靠、高效的通信服务[6],目前已经在智能电网[7]、车联网[8-9]和远程医疗[10]等领域有了广泛应用。

近年来,已有相关学者围绕无线信道中数据业务的时延开展了一系列分析研究。文献[11]提出了一种基于资源预留方式降低uRLLC业务流随机访问时延的方法。文献[12]提出了一种基于马尔可夫链的数值分析方法,可分析出基于竞争的uRLLC上行传输场景中数据包传输的平均时延。文献[13]提出了一个新的基于机器学习的混合自动重传请求(Hybrid Automatic Repeat Request,HARQ)协议,能够减少HARQ操作时产生的延迟,从而降低uRLLC业务的链路传输时延。此外,还有不少学者基于随机网络演算(Stochastic Network Calculus,SNC)分析了多种无线通信场景中用户数据的时延边界,包括慢衰落多入单出(Multiple Input Single Output,MISO)系统[14]、下行非正交多址接入(Non-Orthogonal Multiple Access,NOMA)信道[15]和无线多载波5G网络[16]等。

针对uRLLC业务的上行时延开展研究,通过分析基于半静态调度的初传时延和基于资源竞争的重传时延,推导获得了uRLLC业务的时延上界及分布概率,为研究uRLLC业务的时延性能提供了重要支撑。上述分析方法可以扩展应用到其他业务的无线通信系统时延分析场景中。

本文描述了所关注的uRLLC业务上行传输系统模型;推导了uRLLC业务数据流的时延上界及概率分布,其中包括初传时延和重传时延两部分的建模与分析;介绍了基于NS3的仿真平台,并将仿真结果与理论计算结果进行对比和讨论,验证了理论分析的准确性。

1 uRLLC业务上行无线传输模型

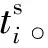
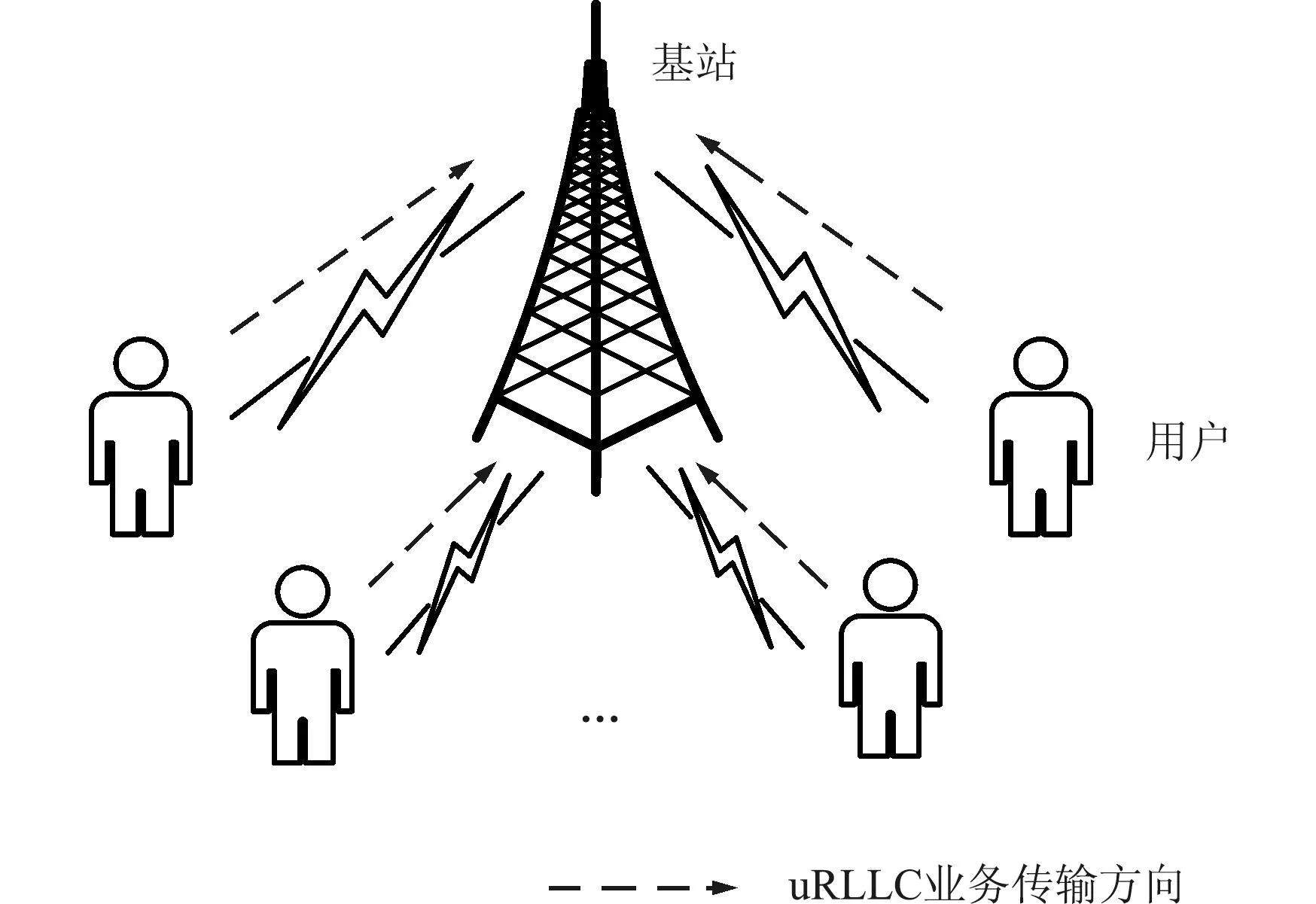
图1 uRLLC业务的无线通信系统模型Fig.1 Wireless communication system model of uRLLC traffic

为了保证数据传输的可靠性,uRLLC数据包在第一次传输(即初传)之后,若未能正确接收,可以进行重新传输(即重传)。在无线通信网络的资源调度中,为uRLLC业务的初传数据包和重传数据包使用不同的调度规则,如图2所示。

图2 uRLLC业务初传与重传的调度规则说明示意Fig.2 Illustration of scheduling rules for initial transmission and retransmission of uRLLC traffic

为了尽可能地保障低时延的传输需求,数据包的初传以半静态调度的方式进行传输。半静态调度的基本思想是仅通过一次信令传输来发送时频资源分配的结果,之后用户可以周期性地使用相同的时频资源,直至通过信令释放所分配的资源[18]。设无线系统时域的最小调度时间为一个时隙,用tslot表示,半静态调度周期用Ti表示,其中i∈[1,NU]。然而,由于无线信道中存在噪声、干扰等不确定因素,数据包在接收端可能会解码错误,设错误概率为pe。为了保证传输的可靠性,允许对传输错误的数据包进行重传。为避免重传数据包对无线资源的过度占用,需要设置最大重传次数(Ntries)。此外,重传数据包以资源竞争的方式获取传输机会。一般情况下,系统为初传预留的资源与重传占用的资源互不重叠。

2 uRLLC业务时延分析

基于上面建立的系统模型可知,任意一个数据包在无线链路上的时延由初传时延和重传时延两部分构成。下面将分别从数据包的初传时延及触发重传机制时的重传时延这2个子场景,分析无线传输部分的时延上界及分布概率。

2.1 初传时延分析

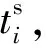
(1)

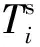
(2)

考虑到业务到达和半静态调度均为周期过程,为保证数据包不会出现积压,同时也保证预留资源不会被浪费,可将半静态调度周期Ti和业务周期τi配置为相同的值,如图3所示。此时,用户i每个数据包的等待时延与第一个数据包的等待时延相同,均为:

(3)

图3 初传排队时延说明Fig.3 Illustration of queuing delay of the initial transmission

数据包被调度之后,经历一段在无线链路的传输时间,用ttrans表示,被接收端接收。因此,用户i的数据包从进入系统到被接收端接收所经历的总时延为:

(4)

2.2 单次重传时延分析

考虑到初传数据包可能因为无线传输信道中噪声、干扰等因素的影响而传输失败,为了保证传输的可靠性,可以对该数据包进行重传。值得注意的是,在无线通信系统的资源分配机制中,重传数据包往往在系统划分好的重传频域资源内以竞争的方式进行调度,即重传频域资源是有限的,在同一个时隙内到达的重传数据包可能会因为资源不够而需要排队等待一个或多个时隙后,才会获得传输机会。

重传频域资源竞争示意如图4所示。假设数据包1、2、3、4分别在A1、A2、A3、A4时刻到达,这些数据包作为初传数据包,会等到半静态调度的时刻(图4中假设为下一个时隙的开始时刻)被传输。假设数据包1、3、4初传失败,则系统会通过信令交互等过程告知发送端该数据包需要重传。定义从数据包接收失败到发送端生成重传数据包所经历的时间为重传生成时间,用tr表示,在本文中设为一个恒定的常数。则发送端会在图4所示的A′1、A′3、A′4时刻生成3个重传数据包。这3个重传数据包竞争有限的重传频域资源。假设一个时隙可用于重传的频域资源数为2,即在同一时隙中最多能同时传输2个重传数据包。因此,3个重传数据包中的一个(图中假设为数据包4)需要等到下一个时隙才能传输,这就导致数据包4的等待时间比数据包1、3多一个时隙。倘若数据包4在第一次重传后仍然未被基站端接收,则会在A″4时刻完成第二次重传数据包生成,并竞争第二次重传机会。

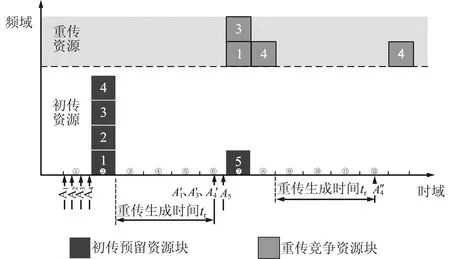
图4 重传频域资源竞争示意Fig.4 Illustration of resource competition for retransmission in frequency domain

根据重传过程可知,重传机制的触发与重传数据包的到达是随机事件,分析重传时延的核心是分析资源竞争过程中需要等待的时隙数,用X表示。它是一个离散随机变量,且满足X∈{0,1,2,…},其概率分布情况与一个时隙内重传频域资源个数N以及数据包传输失败的概率pe密切相关。

设重传数据包不能在当前时隙传输的概率为pR。如图4所示,在A′1时刻到达的重传数据包1成功竞争到了时隙⑦的频域资源,其不需要等待额外的时隙即可完成传输,因此该数据包的重传等待时隙数X=0,对应的概率为1-pR;在A′4时刻到达的重传数据包4由于时隙⑦中的频域资源被数据包1、3所占用,故数据包4需要额外多等待一个时隙,在时隙⑧中传输,即X=1,对应的概率为pR(1-pR)。以此类推,可认为等待时隙数X服从截断几何分布,即:

(5)

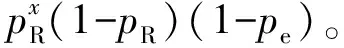
相应地,可以推导出重传数据包在任意时隙中未能正确接收的概率p′,包括2种情况:重传数据包竞争到了资源但是接收端未能正确解码和重传数据包未能竞争到传输机会。

p′=(1-pR)pe+pR。

(6)

假设无线通信系统中用户数目众多,大量互相独立不相关用户的业务聚合在一起的整体特征趋于平稳,极少出现较大的突发。这一特征与传统泊松模型的假设前提相符。基于此,设一个时隙内到达的重传数据包个数为Y,且随机变量Y服从到达率为λR的泊松分布,其中λR为单位时隙内到达的重传包个数,则离散随机变量Y的概率分布满足:

(7)

进一步推导可得:

(8)

为了确定重传业务流的到达率λR,首先需要确定初传业务流单位时隙数据包的到达率λ。根据上面阐述的系统模型可知,用户i持续发送周期为τi的周期业务,所有用户的初传业务流聚合后构成聚合业务流,以时隙tslot为时间单位的聚合流数据包的平均到达率为:

(9)

重传数据包由2种情况构成:初传失败后第一次重传的数据包以及重传数据包失败后再次重传的数据包。因此,重传数据包的到达率λR为:

(10)

将式(6)代入式(10)可得:

(11)

根据重传数据包采取的资源竞争机制可知,单位时隙内到达的重传包个数超过重传频域资源数N的概率P{Y>N},即重传数据包不能在当前时隙传输的概率为pR:

pR=P{Y>N}。

(12)

将式(8)与式(12)联立,并将式(11)代入可得:

(13)

求解式(13)即可获得pR(求解式(13)需要利用数值法。具体而言,首先设置一个极小的误差项ε,寻找满足使式(13)等号左侧与右侧之间的差值小于ε的pR,即为式(13)的数值解。在本文中,误差项ε设置为10-8),将其代入式(5),可以得到重传数据包排队等待的时隙个数X的概率分布。由此,单次重传时延边界可由式(14)给出。对于用户i的任意一个重传数据包而言,其在无线通信系统中完成一次重传的时延可表示为:

(14)

式中:重传生成时间tr和无线链路传输时间ttrans为恒定常数,X∈{0,1,2,…}为离散型随机变量。

2.3 业务流时延边界分析

基于前面的分析可知,一个数据包的总时延由初传时延与重传时延两部分组成,其中重传时延受到等待时隙数X以及重传次数的影响。下面将分情况讨论数据包总时延及概率分布。

情况①:数据包初次传输就被成功接收。

基于式(4)可知,此时数据包的总时延上边界与对应概率为:

(15)

(16)

情况②:数据包初传失败,但经历一次重传后被成功接收。

设第一次重传等待的时隙数为X1,基于式(4)和式(14)可知,此时数据包的总时延上边界与对应概率为:

(17)

(18)

情况③:数据包初传与第一次重传均失败,但第二次重传被成功接收。

设第二次重传等待的时隙数为X2,此时数据包的总时延上边界与对应概率为:

(19)

(20)

情况④:数据包初传、第一次重传至第j-1次重传均失败,第j次重传被成功接收,其中j≤Ntries。

设第k次重传等待的时隙数为Xk,此时数据包的总时延上边界与对应概率为:

(21)

(22)

上述各情况的数据包时延上边界概率总和归一化的条件是参数j和每次重传的重传等待时隙数X均遍历0～∞。但在实际通信系统中,受到最大重传次数的限制j≤Ntries,各时延上界对应的概率总和略小于1。

3 数值结果与仿真验证

上文给出了uRLLC业务初传及多次重传时的总时延及概率分布。为进一步验证理论分析的准确性,基于上面描述的无线传输场景和NS3[19]开源软件开发了相应的仿真系统,以获取无线信道中数据业务时延的仿真结果,并与时延上边界的理论分析结果相对比。

NS3是一款网络仿真器,已经广泛应用于通信系统的建模之中[20-21]。仿真平台在Linux下Ubuntu 20.04 (precise) 64位环境中基于NS3开发实现,模拟了300个uRLLC用户发包的无线传输场景。每个用户的发包起始时刻随机产生,但该用户半静态调度的起始时间为初传数据包产生之后的下一个时隙,且半静态调度周期与数据包发包周期相同,均为16 ms。因此,任意数据包的初传等待时延均小于等于一个时隙长度,即:

(23)

依据3GPP TR 38.802,uRLLC周期业务流数据包大小的典型值为32、50、200 Byte[17],此处设为32 Byte。同时假设一个数据包可以在一个时隙内传输完毕,即ttrans=tslot。系统关键参数配置如表1所示。

表1 参数配置Tab.1 Parameter configuration

重传频域资源数N=10时,不同pe配置下数据包时延的互补累积概率分布如图5所示。可以看出,时延边界的理论计算数值是基于NS3仿真得到的时延结果的上边界。数据包时延随着pe的增大而增大,这是因为pe的增大表明了无线信道状态的恶化,更高的传输错误率往往会导致更高的时延。此外,随着时延的增大,互补累积概率分布下降过程中出现了3个平台,分别对应初传与2次重传。

图5 不同pe配置的时延互补累积概率分布Fig.5 Complementary cumulative probability distribution of delay with different pe

pe=0.1时,改变重传频域资源数N,无线通信系统中数据包时延的互补累积概率分布,如图6所示。可以看到,仍能满足时延边界的理论计算数值是仿真时延结果的上边界。数据包时延随着重传频域资源数N的增大而减小,这是因为N越多意味着在无线信道中可以同时传输的重传数据包个数越多,重传数据包之间的竞争越小,需要等待的时隙个数越少,则数据包总时延越小。同时可以观察到,由于pe保持恒定,不同N取值的曲线中出现的3个平台对应的互补累积概率分布值分别相同。

4 结束语

本文研究了无线通信系统中uRLLC业务的上行时延,从初传时延与重传时延2个角度分别进行时延分析。初传数据包采用半静态调度,重传数据包采用基于资源竞争的调度方法。给出了uRLLC业务数据包在经历了不同传输过程后的时延上界以及对应的概率分布。开发了基于NS3的无线通信仿真系统,并将获得的时延仿真结果与时延理论上界对比,验证了时延上界的有效性。