基于PSO的联合任务卸载与缓存算法研究

周天清，许 铭

(华东交通大学 信息工程学院，江西 南昌 330013)

0 引言

近年来,各类计算敏感(Computation-Sensitive,CS)型和高数据率(High-Rate,HR)服务不断涌现,如移动游戏、认知辅助和虚拟/增强现实服务等。这些服务带来诸多便利和娱乐的同时,也带来了大量挑战:它们往往有较大的任务数据或较高的计算量,导致了移动终端(Mobile Terminal,MT)计算资源和能量紧张的问题,也造成了频谱和回程资源短缺的问题。为缓解MT的压力,云计算技术被提出。通过云计算技术,MT的计算和缓存工作可交由远程云端完成。但是,对于拥有CS和HR服务的MT而言,云计算技术具有明显的缺陷[1]。具体而言,在当今高度拥挤的主干网络上,将所有数据流量传输到远程云端不切实际,尤其是对于高速增长的分布式数据流量。

为克服上述挑战,移动边缘计算(Mobile Edge Computing,MEC)和缓存技术被视为新型网络架构中重要且不可或缺的部分。基于此,MEC网络产生,它将数据服务和计算应用的前沿从云计算中心推向网络的逻辑边缘,从而使得计算和缓存工作能在数据源附近进行。在具备MEC和缓存功能的MEC网络中,计算和缓存服务器被装备到小基站(Small Base Station,SBS),这样不仅可以缩短MT(目的地)与数据源之间的距离,还可以大大减少回程链路的资源消耗[2-3]。

尽管计算和缓存服务器的部署可以极大地支持CS和HR服务,保证较好的用户体验,但可能导致MT关联(选择)更为复杂[3-4]。在具备MEC和缓存的MEC网络中,MT关联不仅涉及基站的选择,还需考虑计算和缓存模式的选择。这意味着,在此类MEC网络中,MT关联可能会变得更为复杂且具挑战性。

近年来,联合边缘计算与缓存的相关研究逐步热化。在计算资源与存储容量的限制下,文献[5]执行MT选择以最小化加权网络时延;文献[6]执行MT选择与资源分配以最优化网络吞吐量、计算与缓存费用。针对大数据MEC网络,文献[7]联合考虑计算、缓存、通信与控制以优化网络时延与带宽消耗;文献[8]联合优化计算卸载决策、缓存部署、MT计算能力与发射功率以折衷网络时延与能耗。在缓存与截止时延约束条件下,文献[9]联合考虑缓存、计算与通信以最小化加权和能耗,涉及软件获取、缓存与广播,任务上传、执行与结果下载。针对2层MEC网络,文献[10]联合考虑数据缓存与计算卸载以折衷网络时延与能耗;文献[11]针对多任务系统,联合考虑计算卸载、服务缓存、功率与计算资源分配以最小化所有MT的计算与延时费用。在缓存、功率与时延约束下,针对双向计算任务模型,文献[12]尝试优化缓存与卸载决策以最小化平均使用带宽。针对边缘服务网络,文献[13]联合执行计算卸载与内容缓存以最小化所有任务的响应时延。针对异构雾无线接入网络,文献[14]研究了联合MT关联、带宽和功率分配以及缓存部署,同时考虑了能量效率和跨层干扰缓解。针对海上通信MEC网络,文献[15]尝试优化任务卸载以降低任务时延与能耗。

上述研究鲜有联合考虑频谱、计算与缓存资源分配,很少涉及多蜂窝场景,且基本考虑有线回程。考虑到CS与HR服务对时延的敏感性,而服务时延直接影响到用户网络体验,类似于文献[3],本文以最小化MT平均时延为目标。同时,在多蜂窝无线回程网络架构下,本文采用与其相同的频带划分机制。不同于文献[3],本文按MT所需资源占其服务基站的所有MT所需资源的比例分配频谱、计算与缓存资源。这种根据需求比例分配资源的方式极大地削减了问题的规模,降低了算法复杂度。另外,本文考虑使用粒子群优化(Particle Swarm Optimization,PSO)[16]开发相应的MT关联与资源分配算法。经仿真验证,在按需求比例分配资源的方式下,该算法取得了较文献[3]算法更优的性能。

1 系统模型

1.1 网络模型

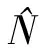
1.2 资源模型

为降低网络干扰,本文采用了频分和时分方案。具体而言,带宽为W的系统频带F被划分成F1和F2两部分,带宽分别为为ηW与(1-η)W,其中η为频带划分因子且满足0≤η≤1;信道相干块T被分割成T1和T2两个时隙且满足T1+T2=T,分别用于上行链路和下行链路传输。此外,假定MT的上下行接入链路使用频带F1,但分别利用时隙T1和T2;假定MT的上下行回程链路使用频带F2,但分别利用时隙T1和T2;在上下行接入链路中,假定F1的 3个等带宽子带F1,1、F1,2、F1,3供不同邻簇使用,其中一个宏小区构成一个簇;在上下行回程链路中,假定F2的3个等带宽子带F2,1、F2,2、F2,3供不同邻簇使用。

显然,通过采用不同的时隙,上下行接入链路间的干扰可以被消除,且上下行回程链路间的干扰也可被消除;通过使用不同的频带,接入链路和回程链路间的干扰可被消除。此外,在上下行接入链路中,任意2个宏小区因使用不同的频带而消除彼此间的干扰;类似地,在上下行回程链路中,任意2个宏小区因使用不同的频带而消除彼此间的干扰。

1.3 通信模型

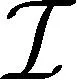
在上下接入链路中,任意子带(如F1,1、F1,2或F1,3)被均分给每个宏小区(簇)内的所有SBS;在上下行回程链路中,任意子带(如F2,1、F2,2或F2,3)被均分给每个宏小区(簇)内的所有SBS;在上下行接入链路中,分配给SBS的频带被切片分配给其所关联的MT;类似地,在上下行回程链路中,分配给SBS的频带被切片分配给其所关联的MT。假定在下行接入和回程链路中,每个基站的频带切片只传输一个文件,这意味着文件索引与基站子信道索引一一对应,它们可以互用。

显然,通过上述频带划分方式,宏小区内任意 2个SBS间的上行接入干扰与下行接入干扰均可被消除;宏小区内任意2个SBS间的上行回程干扰与下行回程干扰均可被消除;小小区内任意2个MT间的上行接入干扰与下行接入干扰均可被消除;小小区内任意2个MT间的上行回程干扰与下行回程干扰均可被消除;在下行接入和回程链路上,小区内任意2个MT传输文件时不会产生相互干扰。

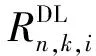
(1)

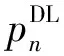
(2)

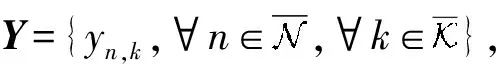
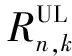
(3)

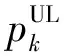
(4)

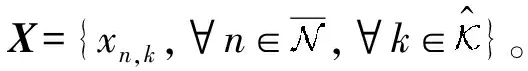
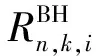
(5)

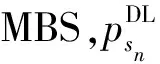
(6)

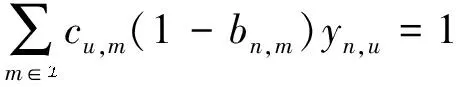
1.4 缓存模型

在现实中,文件请求通常遵循某种分布(例如Zipf分布),这种分布往往可以通过对历史数据流进行统计分析获取。换言之,在仿真过程中,文件的缓存索引可根据某种分布预先生成。值得注意的是,当所需文件已在SBS上缓存时,HRT可直接从其所关联的SBS上获取,否则HRT只能通过所关联的SBS与最近MBS间的回程链路从核心网络获取。

于是,HRTk从SBSn下载文件i所花费的下行接入时间(时延)为:

(7)

HRTk通过SBSn和MBSsn间的回程链路下载文件i所花费的下行回程时延为:

(8)

因此,HRTk从SBSn获取文件i的平均时延为:

(9)

1.5 计算模型

(10)

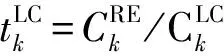
(11)

忽略计算结果下载时间,完成CSTk的计算任务所需时间为:

(12)

2 问题规划

针对MEC网络,为在资源约束条件下提升MT的CS与HR服务的质量,即降低任务计算和文件获取时延,进而改进用户网络体验,本文尝试最小化MT的平均时延,即:

(13)

式中:wk为平均时延权重参数。此外,因为CSTk至多关联至一个SBS,而HRTk必须关联某一个SBS,因此存在:

(14)

在实际系统中,频谱带宽总是有限的。因此,分配给所有CST的上行接入总带宽不能超过它们所关联的SBSn的上行接入带宽,这意味着:

(15)

同时,分配给所有HRT的下行接入总带宽不能超过它们所关联的SBSn的下行接入带宽,即:

(16)

分配给所有HRT的下行回程总带宽不能超过它们所关联的SBSn的下行回程带宽,即:

(17)

此外,任意缓存服务器的存储容量都是有限的。因此,任意SBSn所缓存的文件量不能超过该基站的存储容量Dn,即:

(18)

任意计算服务器的计算能力都是有限的,因此,任意SBSn分配给其所关联CST的总计算资源不能超过该基站的计算资源,即:

(19)

为支持CSTk通过SBSn与最近MBS间的回程链路从核心网络获取文件i,下行接入数据速率应小于或等于下行回程数据速率,即:

(20)

本文所考虑的优化问题可规划为:

(21)

3 PMARA算法

容易发现,式(21)为非线性混合整数优化问题,其最优闭式解难以获取。为处理该类问题,集群智能算法可能是一种不错的选择。目前,此类算法因具有对各类问题的较强适应性而被广泛应用[17-19]。PSO作为集群智能算法的成员之一,因具备收敛速度高、参数少与算法易实现等特点,已被广泛应用于处理各类复杂问题[16]。为求解式(21),提出了基于PSO的MT关联与资源分配(PSO-based MT Association and Resource Allocation,PMARA)算法寻找其最优化解。

3.1 粒子编码

(22)

式中:w1和w2分别为对文件储存超出SBS存储空间和下行回程速率过低的惩罚系数。

3.2 粒子速度及位置更新

(23)

(24)

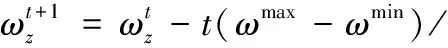
(25)

式中:ωmax和ωmin分别为最大、最小惯性权重,为PMARA算法的最大迭代次数。在PSO中,惯性权重控制着算法的探索能力,更大的可以使算法更容易跳出局部最优,提升搜索能力,而较小的有助于算法收敛。显然,算法迭代初期时的探索能力较强,但随着迭代次数的增加而逐步弱化,算法亦是趋于收敛。

(26)

(27)

式中:ψ(χ)表示对χ向下取整。

为保证全局最佳粒子v向着局部最小值移动,即保证PMARA算法的收敛性,该粒子的速度更新为:

(28)

(29)

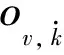
然后,分别将式(28)和式(29)代入式(26)和 式(27),可得全局最佳粒子v的更新位置为:

最后,缩放因子κt可更新为:

(32)

式中:N1和N2分别表示连续成功的次数和连续失败的次数,n1和n2表示阈值参数。当新一轮迭代后的全局最优值与上次迭代后的全局最优值相同时,搜索失败,其他情况代表成功。显然,N1>n1表示算法朝着更优值搜索成功的次数大于n1,此时增大κt以增加粒子朝此方向更新的速度;N2>n2表示朝着更优值搜索失败的次数大于n2,此时缩小κt以降低粒子朝此方向更新的速度;在不满足以上情况时,κt保持不变。

下面给出了PMARA算法的具体流程:

① 利用最佳信道关联(Association with Best Channel Gain,ABCG)规则[3]初始化粒子的位置,利用式(2)、式(4)、式(6)和式(11)计算资源占比,利用式(22)计算所有粒子的适应度值,并设置迭代次序t=1。

② 令初始位置为个体最佳粒子的位置,并从它们中找到全局最佳粒子,最后以(0,1)的随机数初始化个体最佳粒子与全局最佳粒子的速度。

③ 根据式(25)更新普通粒子的惯性权重,并利用式(23)和式(24)更新它们的速度,最后以式(26)和式(27)更新它们的位置。

④ 利用式(28)和式(29)更新全局最佳粒子的速度,并以式(30)和式(31)更新它们的位置。

⑤ 利用式(2)、式(4)、式(6)和式(11)计算资源占比,利用式(22)计算所有粒子的适应度值,最后以式(32)更新它们的缩放因子。

⑥ 更新所有粒子的历史最佳位置,让这些拥有历史最佳位置的粒子为个体最佳粒子,并从它们中找到适应度值最高的粒子作为全局最佳粒子。

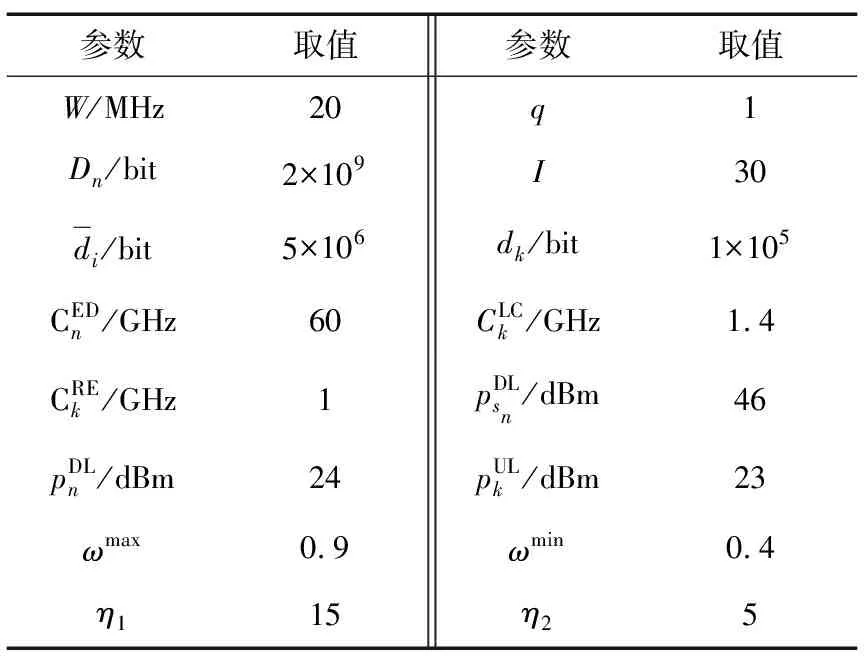
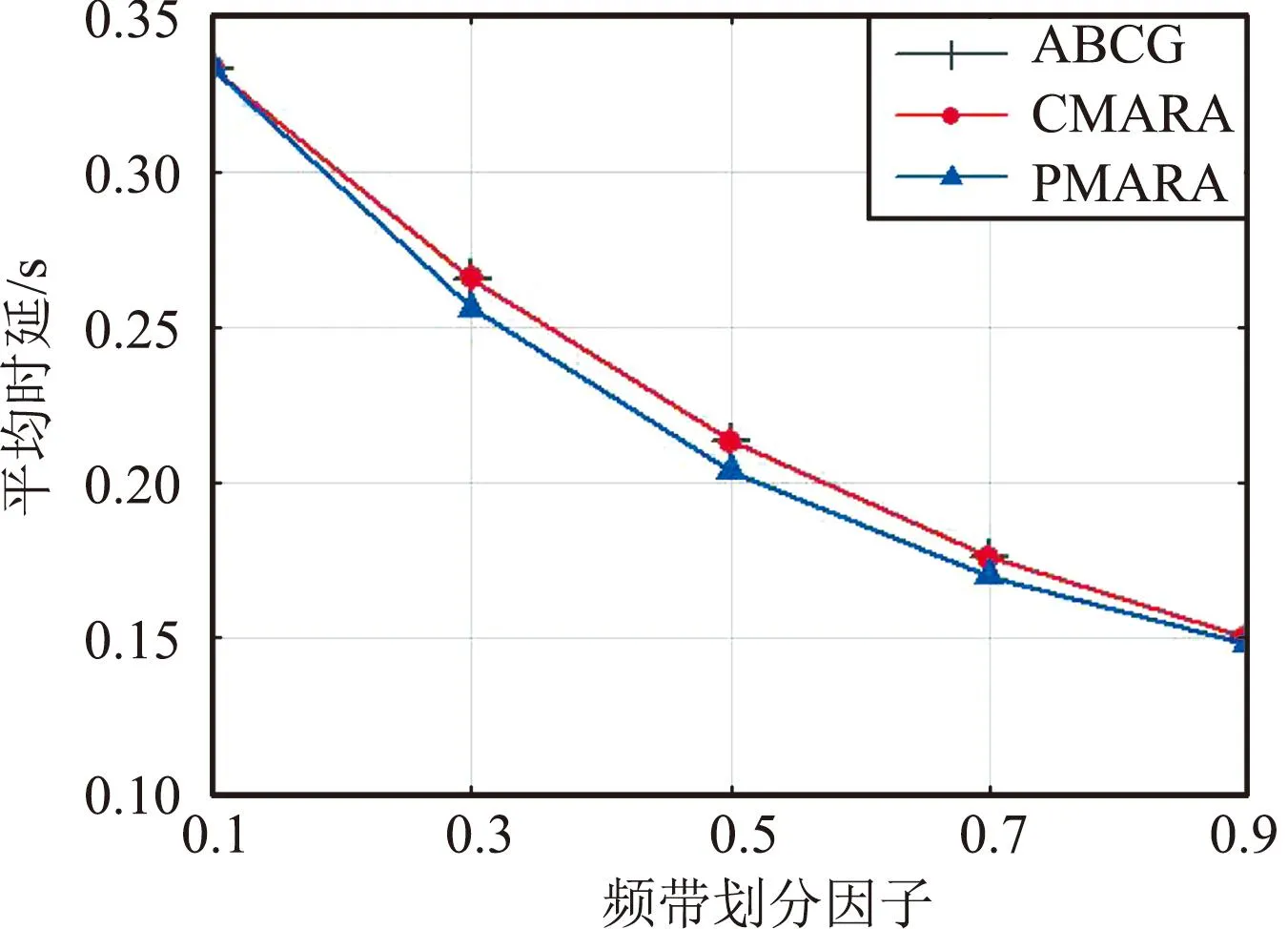
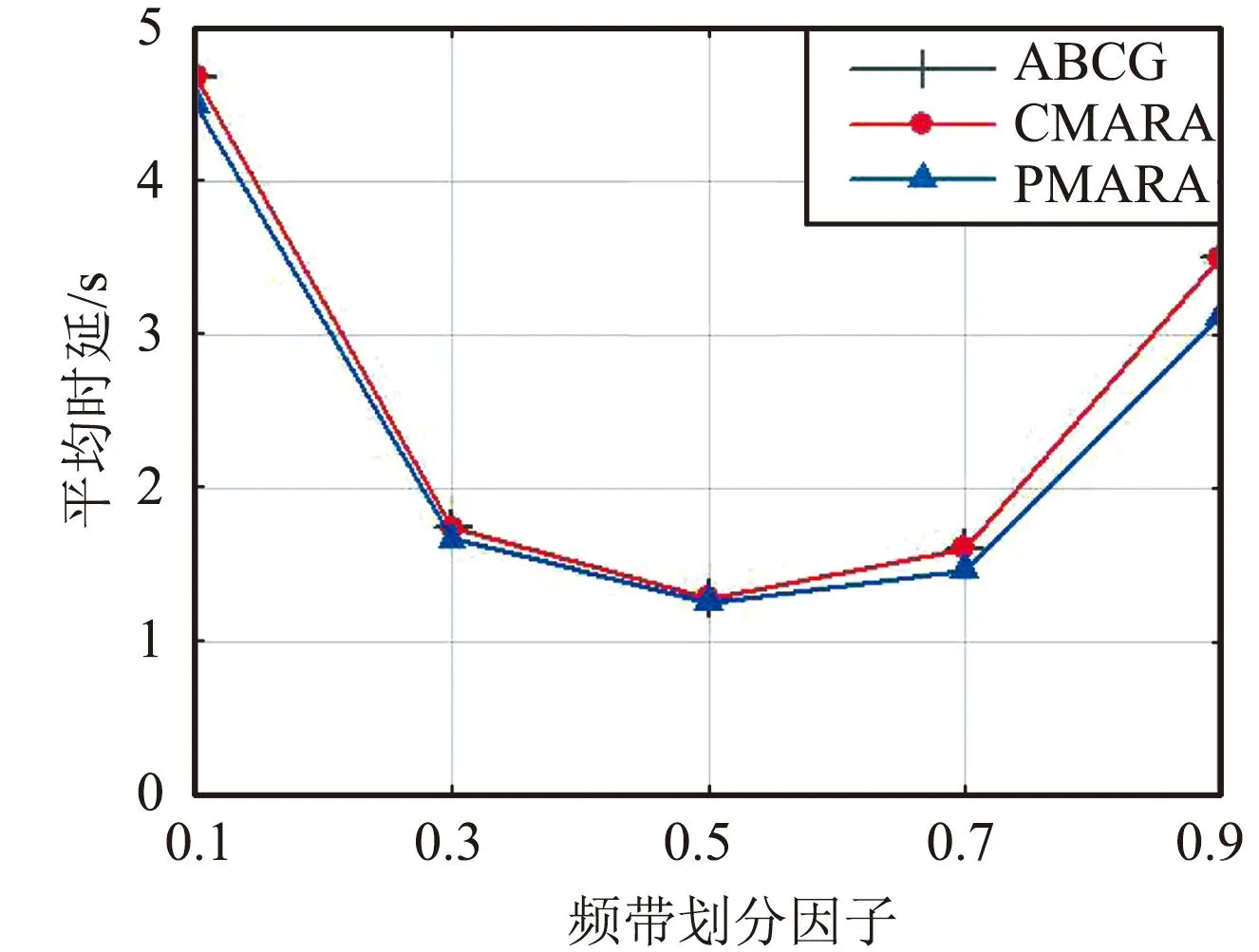
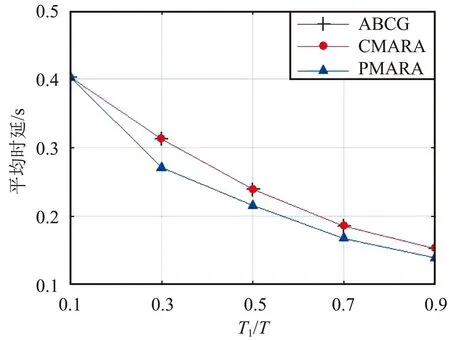
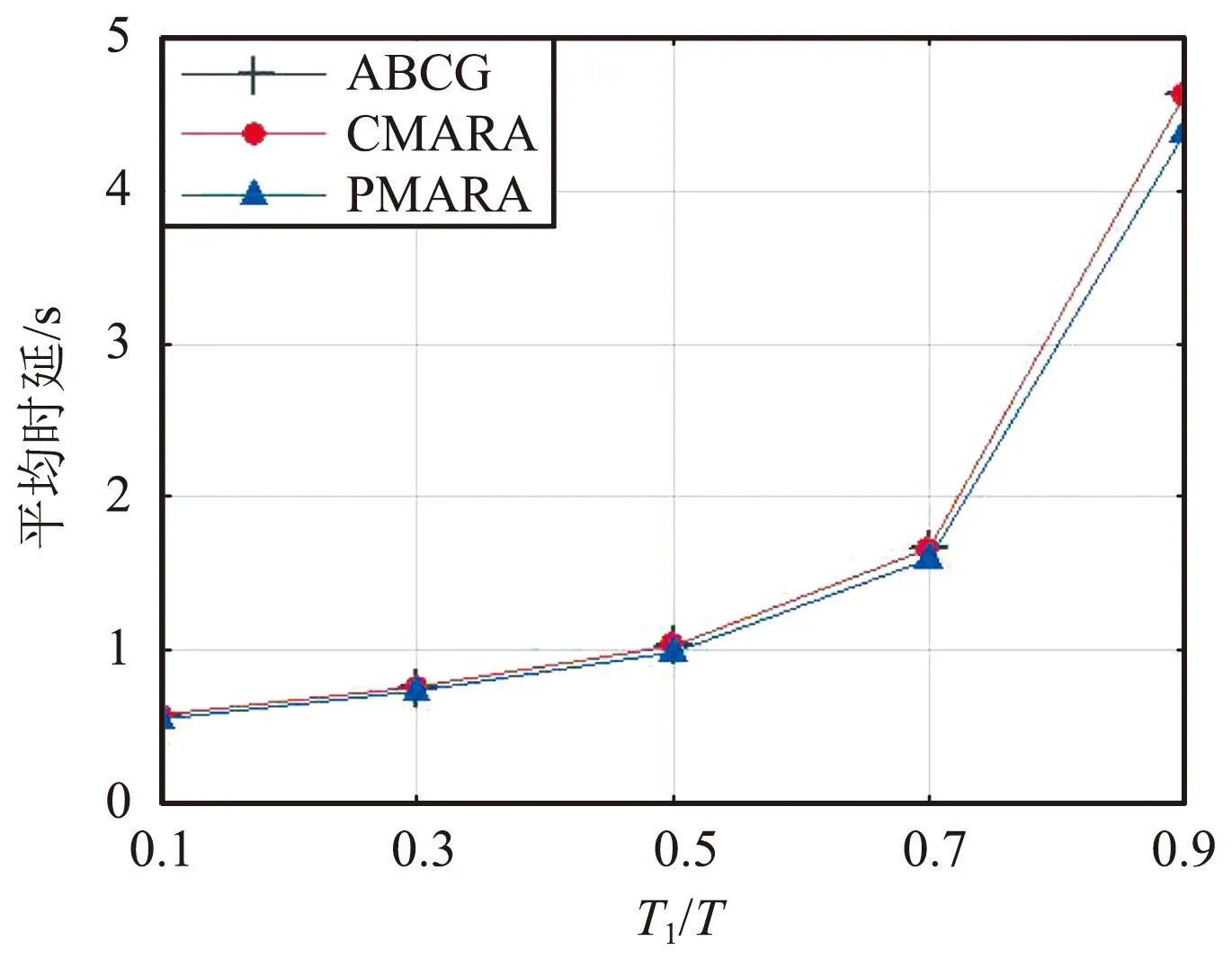
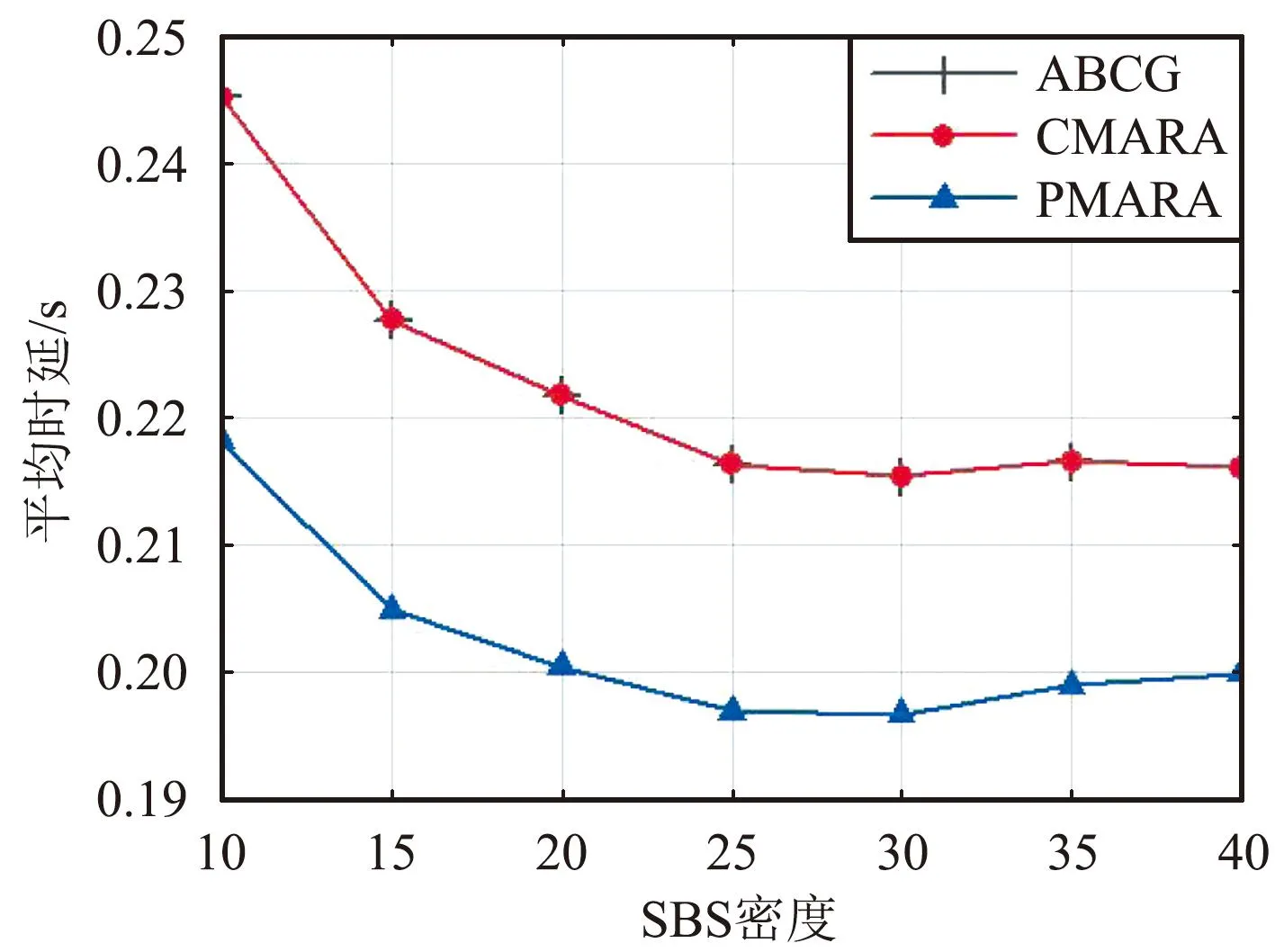
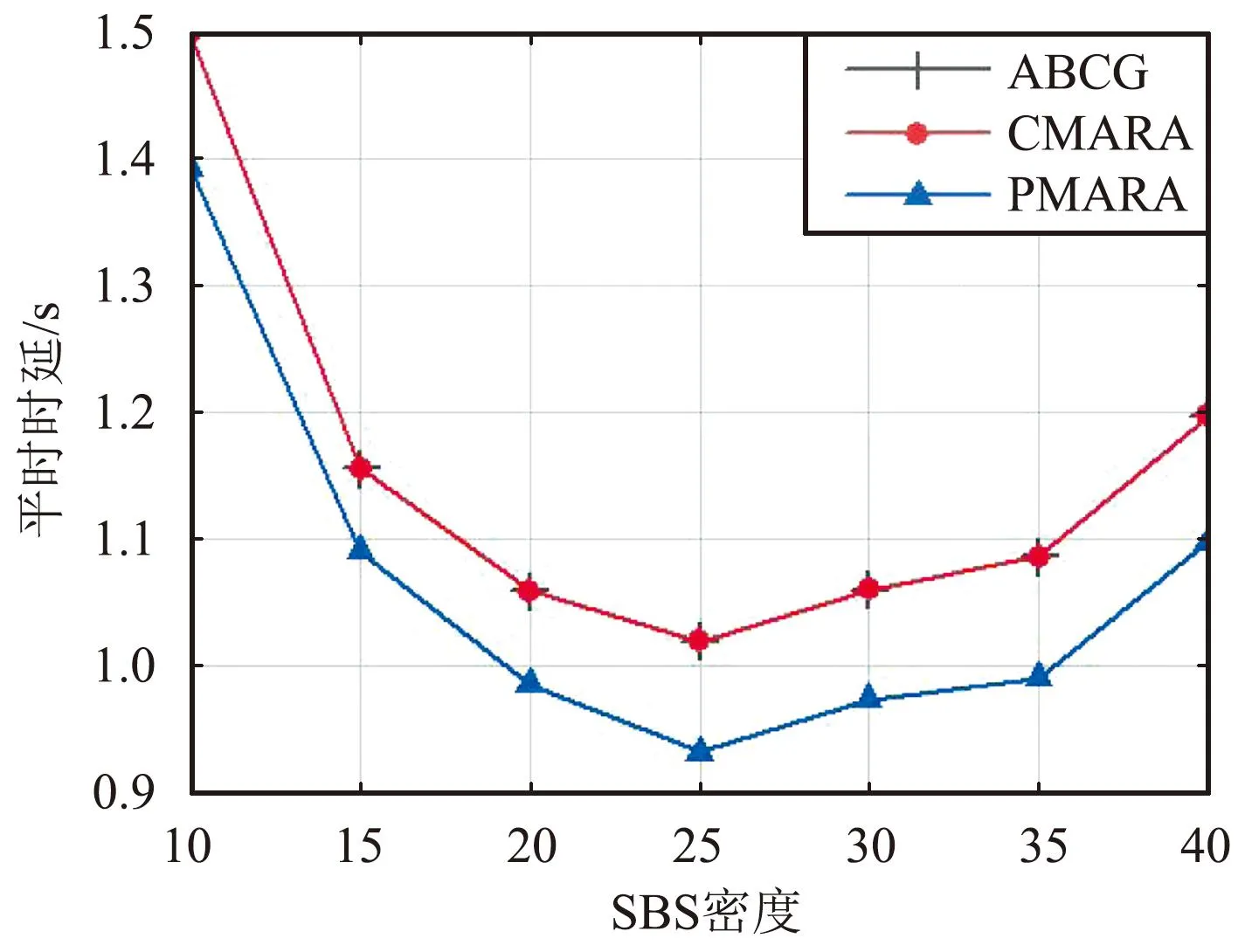
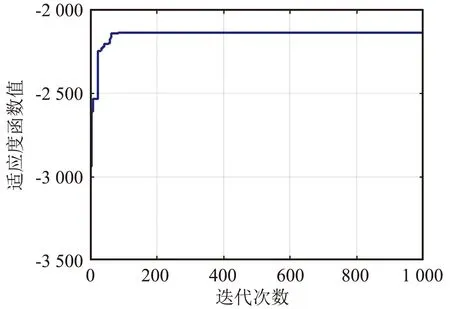
⑦ 更新迭代指示:t=t+1;如果t

在PMARA算法中,① 初始化粒子位置,分配计算资源并计算所有粒子的适应度值;② 初始化个体最佳粒子的位置,确立全局最佳粒子,并初始化这些粒子的速度;③ 更新普通粒子的速度与位置;④ 更新全局最佳粒子的速度与位置;⑤ 重新分配计算资源和计算所有粒子的适应度值;⑥ 更新个体最佳粒子与全局最佳粒子;⑦ 判断PSO算法是否继续迭代,若否则输出全局最佳粒子的位置,最后通过粒子编码规则将其映射为式(21)的解。显然,PMARA算法通过迭代更新粒子的位置从而找到优化 式(21)的解。

4 仿真分析

表1 仿真参数

仿真结果表明,PMARA算法可能获得较CMARA算法更低的时延,CMARA算法达到了与ABCG算法几乎相同的性能。不难发现,ABCG算法用于初始化PMARA和CMARA算法。在相同初始条件下,CMARA算法因不能严格满足资源与速率约束而无法迭代更新其性能,因此达到了同ABCG算法几乎相同的性能;但是,PMARA算法因将这些约束作为惩罚项添加至适应度函数,不需要严格满足这些约束而能迭代更新其性能,因此达到了较ABCG算法更好的性能。

图1显示了频带划分因子η对2类MT平均时延的影响,其中图1(a)和1(b)分别显示了η对CST平均时延和HRT平均时延的影响。因为η的增加导致上行数据速率的增加,所以图1(a)中CST的平均时延随着η的增加而下降。同样,图1(b)中HRT的平均时延也随着η的增加而先下降。但是,在高η域,HRT的平均时延却随着η的增加而增加。其原因在于,随着η的增加,越来越多的MT关联到SBS以获取文件。当MT增加到一定程度时,许多MT因资源不足而不得不通过回程链路从核心网获取文件。这意味着,增加的η会导致回程时延增加。

(a)CST的平均时延

(b)HRT的平均时延

图2显示了占比T1/T对2类MT平均时延的影响,其中图2(a)和图2(b)分别显示了T1/T对CST平均时延和HRT平均时延的影响。因为T1/T的增加导致上行数据速率的增加,所以图2(a)中CST的平均时延随着T1/T的增加而下降。因为T1/T的增加导致下行数据速率与下行回程数据速率的下降,所以 图2(b)中HRT的平均时延随着T1/T的增加而增加。

(a)CST的平均时延

(b)HRT的平均时延

图3显示了SBS密度ρ(宏小区内MT的个数)对2类MT平均时延的影响,图3(a)和图3(b)分别显示了ρ对CST平均时延和HRT平均时延的影响。因为ρ的增加导致MT越发接近服务基站,其上行数据速率随之增加,所以图3(a)中CST的平均时延均随着ρ的增加而下降。但是,因为ρ的增加导致MT越发接近服务基站,其下行数据速率随之增加,所以图3(b)中HRT的平均时延初始随着ρ的增加而增加。但是,当SBS密度增加到一定程度时,用户接收的下行干扰带来的损耗将超过拉进服务距离带来的增益,因此图3(b)中HRT的平均时延后期随着ρ的增加而增加。

(a)CST的平均时延

(b)HRT的平均时延

图4显示了PMARA算法的收敛情况。可以看出,PMARA算法具有较快的收敛速度,能在有限迭代次数内找到优化问题的解。

图4 PMARA算法的收敛情况Fig.4 Convergence of PMARA algorithm

5 结束语

为满足CS和HR服务需求,针对具备边缘计算与缓存功能、支持无线回程的多蜂窝MEC网络,本文首先按需求比例分配频谱、计算与缓存资源,然后开发出PMARA算法以最小化所有MT的时延之和。总体上,PMARA算法可获得较其他现有算法更低的MT(包括CST和HRT)时延。这意味着, PMARA算法能更好地满足2类MT分别对CS和HR服务的通信需求。在未来工作中,可融入非正交多址接入以提升网络资源利用率,并考虑上行功率控制以降低网络能耗与干扰。