基于预报气温和HS公式估算麦季参考作物蒸散量

刘小飞，谢朝晖

（河南城建学院生命科学与工程学院，河南平顶山 467036）

0 引言

河南、山东、河北是华北平原生产冬小麦的大省，在生产冬小麦时面临农业水资源短缺的压力及肥料利用率低等问题[1-2]，沿黄地市灌溉水主要来源于黄河水和地下水。近些年来，黄河水资源短缺，且冬小麦生长季节正值黄河枯水期，不能保证当地灌溉水量的需要，主要靠抽取地下水进行灌溉，这就导致地下水位下降，从而引起地下水漏洞区的出现以及灌溉电费成本的增加等问题，因此必须进行科学合理的灌溉用水计划[3]。灌溉预报是实施灌溉用水计划的主要方法，其本质是根据天气预报资料估算作物耗水量和预报降雨资料进行对比分析，然后做出抉择，确定灌溉水量和灌溉时间。

预报未来短时期作物蒸散量大多采用参考作物系数法，当作物系数确定后，参考作物蒸散量的估算精度成为灌溉预报的重要指标。运用天气预报资料估算参考作物蒸散量主要采用以下几种方法。

（1）基于气象资料采用Penman-Monteith(PM)方程[4]估算参考作物蒸散量[5-6]。刘钰等[7]系统地介绍了气象数据缺测条件下参考作物蒸散量的计算方法，这为以后用气象资料估算参考作物蒸散量提供了理论和实践基础。之后，蔡甲冰等[8]对这一方法进行了完善和改进。

（2）基于气象资料采用Hargreaves-Samani(HS)公式[9]估算参考作物蒸散量[10-13]。

（3）基于气象资料采用Blaney-Criddle 方程[14-15]估算参考作物蒸散量。

（4）基于数值天气预报[16-18]和数学算法（神经网络[19-20]、符号算法[21]、基因表达[22]等）估算参考蒸散量。由于数值天气预报和数学算法估算参考作物蒸散量需要配置昂贵装备，并且不易于被农业科技人员掌握运用，目前计算参考作物蒸散量应用最多的为Penman-Monteith公式和Hargreaves-Samani公式。

在用Penman-Monteith 公式估算参考作物蒸散量时，必须用到的气象数据包括最高温度、最低温度、风速、日照时数、湿度5种。常用的气象预报要素包括最高气温、最低气温、天气情况（晴、阴、多云、大雨、小雨、暴雨等）、风向和风力等级，不能满足Penman-Monteith公式计算的条件。有研究者[23]通过天气预报数据估算采用Penman-Monteith 公式计算蒸散量过程中所需要的太阳辐射和水气压，均取得了较好的精度，但计算过程比较复杂。但其前提条件是天气预报数据的精度要足够高。而运用Hargreaves-Samani 公式计算参考作物蒸散量只需要气温资料，采用较少气象数据估算参考作物蒸散量的优点在于不需要较多的气象要素，只要能满足精度要求，操作方便，简单易懂，对比天气预报数据和气象数据的差别，气温成为首选气象要素，只有气温为具体的数值，其它几项天气预报数据都为范围值。因此本研究拟采用预报气温数据和Hargreaves-Samani公式估算参考作物蒸散量，以Penman-Monteith公式计算的参考作物蒸散量作为参照标准。本研究旨在探讨Hargreaves-Samani 公式在华北地区冬小麦生长季节的适用性。

1 材料与方法

1.1 试验地概况

新乡地处113°54′E，35°18′N，属暖温带大陆性季风气候，四季分明，冬寒夏热，秋凉春早，年平均气温14℃，最高气温42.7℃，最低气温-21.3℃。年平均空气湿度68%，最大冻土深度280 mm。年平均降水量656.3 mm，最大降水量1168.4 mm，最小降水量241.8 mm，最大积雪厚度395 mm，年蒸发量1748.4 mm。6—9月降水最多，可达409.7 mm，占全年降水的72%，且多暴雨。年平均日照时数1928.5 h，无霜期220 d[23]。

1.2 数据来源及冬小麦生育期月份定义

本研究采用的河南省新乡市气象资料来自国家气象中心(http://data.cma.cn/)，包括最高气温(℃)、最低气温(℃)、10 m高处平均风速(m/s)、相对湿度(%)、日照时数(h)。新乡历史天气预报数据来自天气网(https://www.tianqi.com/)，主要包括最高气温(℃)、最低气温(℃)、天气、风力风向。由于涉及年份较多，假定每年10月1日—次年5月31日为冬小麦生长月份。

因此，快递公司加强对快递网点（不要管他是一级还是二级网点）跨区行为的管理、维护基层网点的合法权益，不仅是维护这些基层网点和员工的利益，更是在为了维护公司的自身和长远利益，那种只顾眼前不图长远的经营理念，不仅是对下属员工的不公平不负责，也是对公司的不负责甚至可以说是对老板自己的不负责任。在呼吁和期望政府提供公平公正市场环境的同时，我们快递公司的老总们也该扪心自问一下：你的公司内部营商环境是否公平公正呢！

1.3 测定蒸散原理与方法

1.3.1 彭曼-蒙太斯(Penman-Monteith)公式 1998年FAO 专家咨询会议推荐使用的Penman-Monteith 公式如式(1)[4]。

式中：ET0pm为日参考作物蒸散量(mm/d)；Rn为净辐射量MJ/(m2·d)；G为土壤热通量MJ/(m2·d)，在本研究G取0；Δ为饱和水汽压与温度关系曲线的斜率kPa/℃；γ为湿度计常数kPa/℃，取值0.066 kPa/℃；T为空气日平均温度℃；u2为地面以上2 m高处的风速m/s；es为空气饱和水汽压kPa；ea为空气实际水汽压kPa。

1.3.2 Hargreaves-Samani公式形式如式(2)。

式中：Tmax为日平均最高气温℃；Tmin为日平均最低气温℃；Ra为大气层顶太阳辐射MJ/(m2·d)。

1.4 评价指标

评价指标主要包括平均偏差误差(MBE)、平均绝对误差(MAE)、均方根误差(RMSE)、相对均方根误差(RSE)和拟合度(IA)，各评价指标计算公式如式(3)～(7)。

式中：N为测定值的数量；Oi为测定值，上划线代表均值；Pi为预测值，上划线代表均值。

2 结果分析过程

2.1 预报日气温的精度验证

统计2018—2019年和2019—2020年两个冬小麦生长季节的逐日气象预报的最高气温和最低气温的预报值和观测值，其变化过程见图1a 和2a，并分别对最高气温和最低气温的预报值和观测值进行了线性拟合关系，其结果如图1b 和2b 所示。由图1a 和2a 可以看出，最高/最低气温的预报值和观测值的变化过程一致，都随时间推移呈V 字形变化，最高/最低气温的变化范围分别在35℃和25℃之内；在小麦生长阶段，预报气温略低于实测气温。由图1b和2b可以看出，模拟方程的决定系数均在89%以上；预报的最高/最低气温与实际观测值的MBE分别为-0.49℃和-0.60℃，RMSE分别为1.60℃和2.52℃，总的说来，天气预报对日高温的预报精度较高。

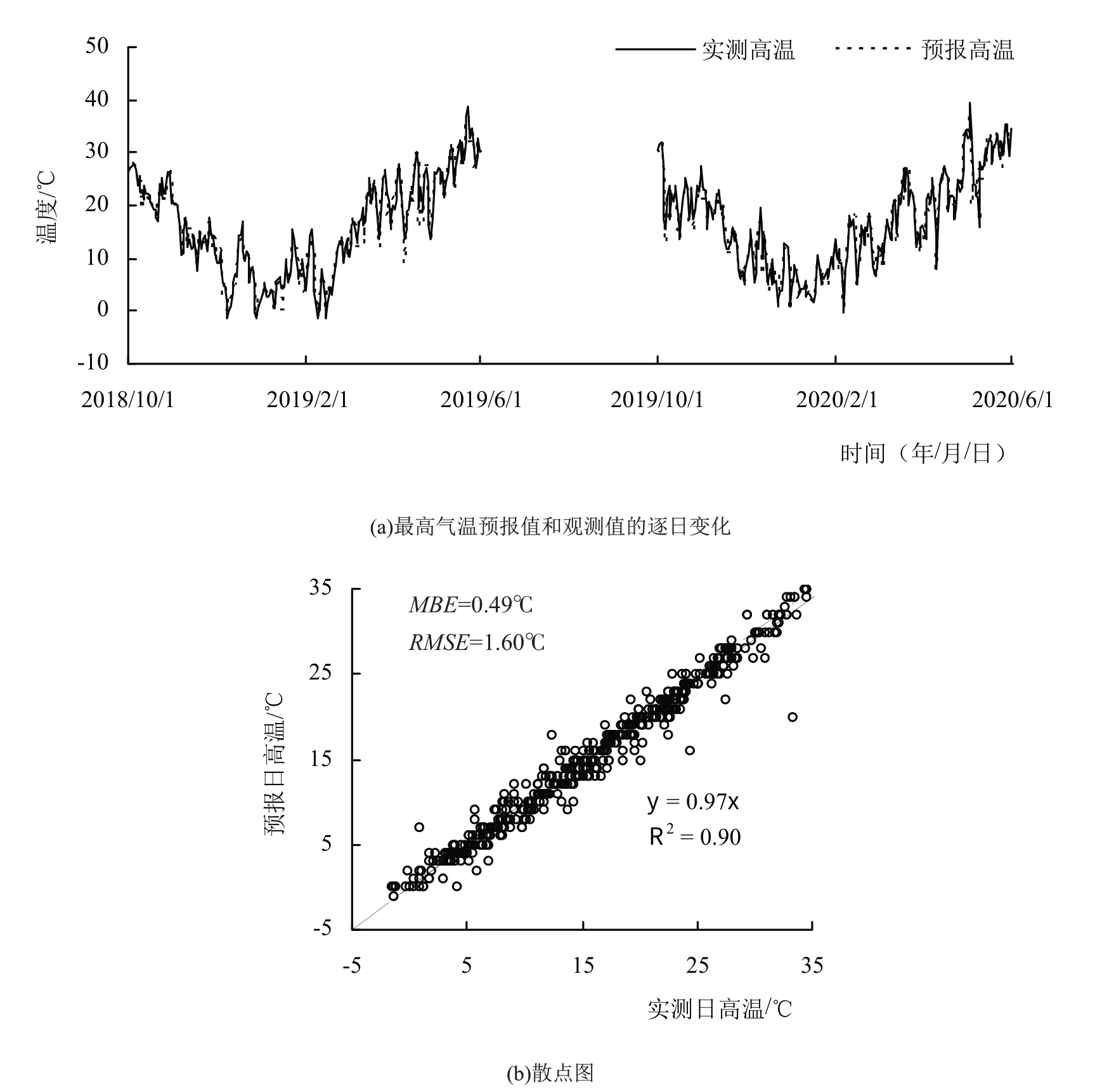
图1 2018—2020年小麦生长季日最高气温预报值和观测值的逐日变化(a)和散点图(b)

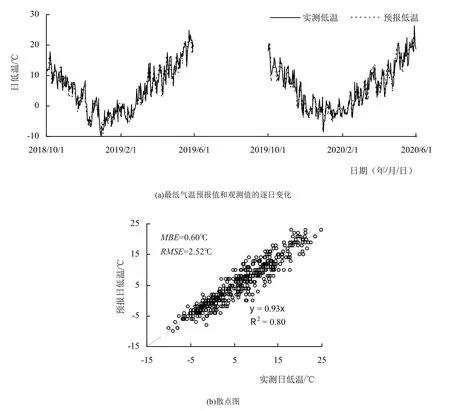
图2 两个试验年度小麦生长季日最低气温预报值和观测值的逐日变化(a)和散点图(b)

2.2 HS公式参数的率定

HS 公式中的系数0.0023 是在美国加利福尼亚州戴维斯试验站点用29 m2称重式蒸渗仪进行了8年牧草蒸散量的基础上计算出来的经验系数，这一系数是否能在新乡地区使用，为此必须进行当地参数化校正。假设在新乡地区的系数为khs，公式(2)变形为式(8)。

运用PM公式计算1961—2013年冬小麦生长季节每天的参考作物蒸散量作为(8)式的计算结果，并把对应日的最高、最低气温和外空辐射项带入式(8)，得到冬小麦生长季节各月的khs系数（表1），khs的平均数为0.002280。与原作者[9]推荐值0.0023比较接近。

表1 冬小麦生长季节各月的khs系数值

2.3 预报参考作物蒸散量的验证

以2018—2020年冬小麦生长季节气象资料采用PM 公式计算的参考作物蒸散量作为实际值，以对应日的天气预报温度资料采用修正后平均系数为0.00228 的HS 公式计算的参考作物蒸散量作为预报值。

图3 绘出了冬小麦逐日参考作物蒸散量变化过程，从图3 中可以看出，两年的变化趋势基本一致，从10月逐渐下降，至次年1月降至最低，在2月中旬逐渐上升的过程，参考作物蒸散量最大值在8 mm/d。HS估算值总体小于PM 估算值，表现在二者平均偏差误差为0.01 mm/d。从散点图4 中可以看出，在4、5月温度越高，二者偏差加大。总体来说，表2 为采用HS 估算参考作物蒸散量的误差统计参数表，从表2 中可以看出，平均绝对误差为0.48 mm/d，均方根误差为0.64 mm/d，决定系数为0.80，拟合度为0.96，说明采用预报气温和HS公式估算参考作物蒸散量能满足精度上的要求，可以在华北地区应用预报气温和HS 公式估算参考作物蒸散量。

表2 预报参考作物蒸散量和实际值的误差统计参数

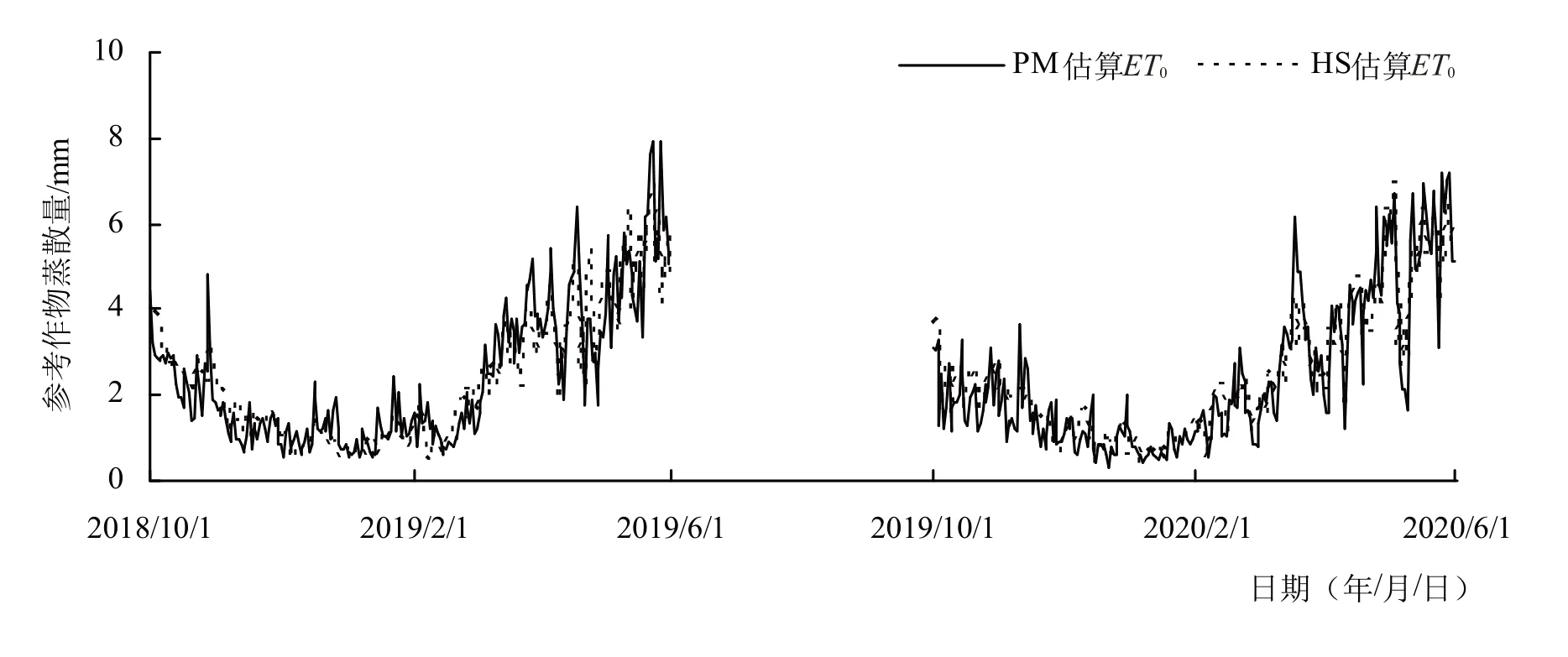
图3 分别用HS和PM估算参考作物蒸散量的日变化过程图

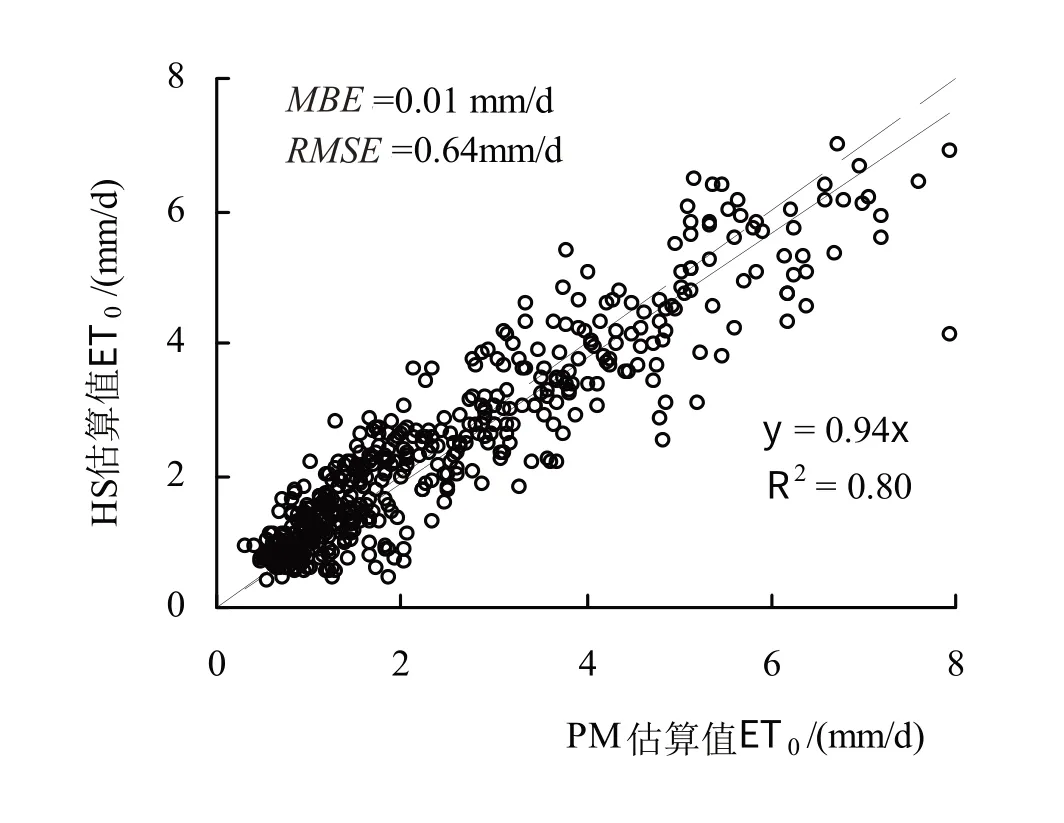
图4 分别用HS估算和PM估算的参考作物蒸散量的散点图

3 结论与讨论

（1）应用气温资料估算参考作物蒸散量可以避免应用PM公式中一些复杂的参数处理问题。例如应用PM 公式时需要估算太阳辐射和水气压，计算太阳晴空辐射时as和bs数的确定。如果没有多年实测的太阳辐射值来标定参数as和bs，推荐采用as=0.25，bs=0.50。1963年，左大康等[24]提出郑州地区as=0.24，bs=0.717。1981年王懿贤等[25]对系数进行了季节性修正，采用取值如下：as，0.152（春）、0.115（夏）、0.301（秋）、0.172（冬）；bs，0.556（春）、0.588（夏）、0.311（秋）、0.536（冬），相应四季的划分为阳历3—5月为春季，6—8月为夏季，9—11月为秋季，12月—翌年2月为冬季。宋妮等[26]在参考作物系数时也用了王懿贤推荐的参数，本研究也采用王懿贤推荐的参数计算参考作物蒸散量。

（2）本研究中率定HS方程中系数khs，只用了khs一个系数，也有学者[27]用3 个系数来率定HS 方程，其方程的形式见式(9)。

式中：C、E、T为HS公式的3个参数。

本研究运用了一个参数，其理论根据是1982年Hargreaves提出见式(10)。

式中：

把式(10)带入式(11)得到公式(12)。

公式(12)中，KRS通常取0.17，公式(12)变为公式(2)的形式。本研究认为，式(10)和式(12)中系数KRS可以根据当地气象要素校正，指数项0.5和常数项17.8都为固定值，改变固定值可能会改变原公式(8)的本意，再者，校正一个参数从对数据的处理上来说比较容易而且精准。

在新乡地区参数的对比过程中发现，陶国通等[28]运用了3 个参数，建议参数C、E、T，建议值分别为0.0023、0.5、17.8，各率定参数分别为0.0018、0.489、22.192，拟合方程相关系数r为0.903，张倩等[29]也运用了3个参数，各修正参数分别为0.0017、0.5、24.6，修正后拟合方程的决定系数R2由0.82提高到0.97。陶国通和张倩的参数比较接近，本研究率定参数0.00228和原公式建议参数0.0023比较接近。

（3）用相同的气象资料估算参考作物蒸散量时，HS 公式在干旱地区估算值低于PM 公式估算值而在湿润地区估算值高于PM公式估算值[30]。本研究所属半干旱区域的干旱季节，估算值偏低。气温预报误差会导致预报值与PM公式计算结果的相差较大[31-33]，对于本研究来说，用HS 公式估算参照作物蒸散量整体值偏低的最主要的原因在于预报温度偏低和研究区域属于半干旱地区的干旱季节。后期温度过高偏差增大的结果与文献[34-35]的结果一致，究其原因，可能是高温期间其它气象因素在估算参考作物需水量的贡献加大，而HS公式只考虑了气温的影响，没有考虑其它气象因素。

（4）本研究对依据天气预报中气温资料结合HS方程估算参考作物蒸散量进行了详细的阐述，应用前提是预报温度的精度要高，其模拟的相关系数为0.91，拟合度为0.93，模拟精度较高，说明运用预报气温和HS 公式估算参考作物蒸散量在华北地区可行。运用HS公式形式简单，容易上手，要推广到其它地区的话，必须进行当地的参数校正，结合当地的预报气温和降雨，指导当地的灌溉计划。