基于MPC的履带车步进行驶控制器设计

宋秋杰,熊树生

(浙江大学,浙江 杭州 310012)

0 引言

机场跑道建设是机场建设的重中之重,基于滑模摊铺的混凝土施工技术多应用于机场停机坪等大面积混凝土摊铺工程,可以在保证施工质量、效率的同时控制成本,近年来逐渐成为机场道路摊铺的主流方案[1]。由于滑模摊铺特殊的施工方式,尽管摊铺机能够快速高质量完成摊铺作业,其铺设的道面仍需要人工进行抹平抹光、拉毛养护等后处理工作,如图1所示。

图1 滑模摊铺及其人工后处理

我国滑模摊铺技术引入较晚,缺乏高素质的摊铺后处理技术工人,往往需要投入大量人力完成后处理工作,人工处理速度慢,道面后处理质量参差不齐,提高了施工成本的同时极大地影响了道路摊铺效率。

针对上述问题,亟需一种自动化后处理作业车,代替人工进行道面后处理工作。本文基于该智能车工作的重难点,对其行驶控制器进行理论分析与开发设计,实现后处理智能车自动步进行驶功能,为项目开发奠定理论基础。

1 智能车动力学建模

根据施工要求,本文研究对象的结构示意图如图2所示。

图2 摊铺后处理智能车结构示意图

如图所示,该车为履带车,由于履带结构的特殊性,其在正常行驶的过程中必然伴随着较为明显的滑移滑转现象,因此该车的运动学模型示意图如图3所示[2]。

图3 履带车运动学示意图

图中,考虑滑移滑转时,Or为转向中心,v1r为低速侧履带实际速度,v2r为高速侧履带实际速度,vr为履带车实际速度,ωr为车辆实际横摆角速度,Rr为车辆实际转向半径,B为左右履带间距。不考虑滑移滑转时,ω为车辆横摆角速度,v1为低速侧履带速度,v2为高速侧履带速度,R为履带车转向半径。由图可知,相较于无滑移滑转的情况,实际履带车低速侧履带速度增加,高速侧履带速度减小,车辆转向半径增大。根据运动学关系,可以得到:

(1)

考虑滑移滑转的动力学示意图如图4所示。图中,O1、O2分别为左右履带的瞬时转动中心,A1、A2分别为左右履带的转向极(即瞬时转动中心距履带中心的距离),P(x1,y1)、Q(x2,y2)分别为左右履带上的一点,vp、vq分别为P、Q点相对地面的滑动速度,vpx和vpy分别为P点滑动速度在x轴和y轴上的分量,vqx和vqy分别为Q点滑动速度在x轴和y轴上的分量,Fp和Fq分别为P、Q点受到的滑动摩擦力,θ1和θ2分别为vp、vq和各自履带中轴线的夹角,F1、F2分别为左右履带受到的纵向滑动摩擦力,f1和f2分别为左右履带受到的行驶阻力,是由履带车机械结构决定的。M1和M2分别为左右履带受到的行驶阻力矩。

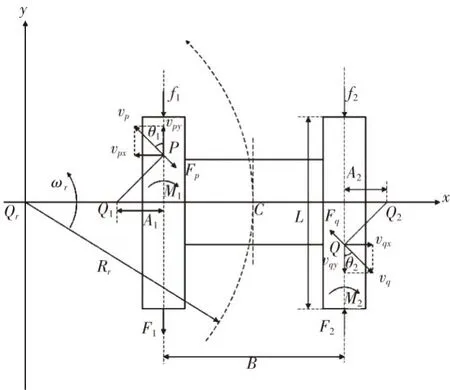
图4 履带车动力学示意图

根据几何关系结合力学分析可得:

(2)

由于履带受力均匀且忽略履带宽度的影响,因此有:

(3)

式中,G为车辆重量,φ为地面摩擦因数。

根据运动学原理有:

(4)

对低速侧履带中心点取矩,根据力与力矩平衡条件可以得到:

(5)

式中,f为行驶阻力系数。联立上述公式,解超越方程即可求得未知量A1和A2。根据运动学关系可得:

(6)

在左右履带理论线速度v1和v2已知的情况下,根据已求得的A1、A2,结合公式(5)和公式(6)即可求得ωr和Rr。至此,履带车动力学模型求解完成。

(7)

(8)

2 四次多项式步进轨迹规划

2.1 轨迹规划坐标转换

四次多项式轨迹曲线表达式如下:

(9)

式中,S为前方车道线上某点相对摄像头所在直线的横向偏移距离,Sy为车道线上某点距摄像头的纵向距离。K1～K5为三次多项式系数。对于沿该多项式行驶的车辆,其横向加速度与纵向距离的对应关系为:

(10)

步进轨迹需要保证沿该轨迹行驶的履带车不会与待施工路面发生碰撞,履带车接地部分仅有两侧履带,因此在碰撞分析时仅需考虑履带与路面的接触情况。为便于分析,将履带简化为长为L,宽为b的长方形,两侧履带中心距为B,左右履带内侧顶点分别为M、N、P、Q,如图5所示。

图5 履带简化与参数定义

设沿轨迹行驶的履带车几何中心点的坐标为Q(x,y),履带车横摆角为φ,如图6所示,则四个顶点的坐标可以通过几何关系求得。

图6 轨迹上某点的坐标转换

M点坐标为:

(11)

N点坐标为:

(12)

P点坐标为:

(13)

Q点坐标为:

(14)

2.2 轨迹规划碰撞约束

为使履带车行驶时不会与待施工路面产生碰撞,需要对履带顶点位置做出限制,设待施工路面宽度为D,安全距离为i,如图7所示。

图7 碰撞约束

(15)

2.3 轨迹规划优化函数设计

为保证步进的整个过程中履带车行驶平滑稳定且步进结束时平稳停车,定义关于车辆最大曲率、最大急动度及终点曲率的代价函数[3]:

J=aρ2+bj2+cσ2

(16)

其中,ρ为轨迹最大曲率,j为轨迹最大急动度,σ为轨迹终点曲率,a、b、c为权重系数。

最大曲率、最大急动度的求解会在每一次迭代中再求解一次参数极值,若采用优化算法进行迭代求解,理论较为复杂且算力要求较高。为满足工程需求,将最大曲率和最大急动度用插值代替,即:

(17)

式中t代表采样时刻。由于四次多项式曲线是连续且平滑的,因此只要采样频率足够,且每项插值均满足约束条件,则插值优化函数可以保证整个曲线接近最优曲线。

在整个步进过程中,定义φ(t)为采样时刻t的车辆运动状态,S为整个步进过程中的运动状态合集。即:

φ(t)= [ρt,jt,yt,φt]T∀t∈[1,Nend]

(18)

S=[φ(1),φ(2),…φ(Nend)]

(19)

用lr(t)、hr(t)分别表示在采样时刻t,车辆的运动状态约束,并用LR和HR分别表示整个步进过程中的上下边界条件。即:

(20)

(21)

综上所述,四次多项式轨迹规划优化函数为:

s.t.LR≤S≤HR

(22)

至此,四次多项式轨迹规划转化为求解上述优化问题,通过设置合适的权重系数,利用MATLAB提供的fmincon函数,采用默认的内点法或有效集法即可求得优化后的四次多项式轨迹。

3 MPC轨迹跟踪控制器设计

3.1 MPC基本原理

模型预测控制机理如图8所示[4],包含三个重要环节:预测模型、滚动优化、反馈矫正。基于本文讨论的轨迹跟踪控制问题,三个环节的内容可以概括为:

图8 MPC基本原理

1)预测模型:即车辆动力学模型。

2)滚动优化:在下一时刻,需要再次测量该时刻的状态量,并将其作为初始条件重新进行优化求解。

3)反馈矫正:状态量与参考量之间的差值作为反馈信息,构成整体的闭环控制。

3.2 非线性MPC理论模型

根据车辆运动学规律,履带车在步进过程中满足:

(23)

根据以上公式,取状态量:χ=[x,y,φ]T,控制量:u=[v,ω]T。对于履带车控制系统,任意时刻的状态量和控制量均满足:

(24)

某一时刻,在任一点(χr,ur)处,根据泰勒定理,保留一阶项,忽略高阶项得:

(25)

根据公式(23)、(24)和(25),状态量误差的变化量为:

(26)

定义离散时间间隔为T,对公式(26)进行前向欧拉离散化可得:

(27)

在非线性MPC控制算法中,采用目标函数:

(28)

该目标函数中的第一项反映了该控制算法对目标轨迹的跟踪能力,第二项反映了该控制算法中控制量变化的平稳性,第三项ρ为权重,ε为松弛因子,避免出现优化问题无解的情况。

3.3 线性MPC理论模型

(29)

其中,Nc=2为控制量个数,Nx=3为χ的状态量个数,η为状态量输出方程。在满足控制精度的情况下,尝试简化计算,做出如下假设:

对控制周期内任一时刻下的状态方程有,

Ak=A,k∈[1,…,t+N-1]

Bk=B,k∈[1,…,t+N-1]

(30)

在该假设条件下,对公式(29)进行递归计算:

(31)

归纳总结得到状态量ξ的输出方程为:

(32)

由上式可以看出,根据当前时刻的状态量ξ(k)和控制时域内的控制增量ΔU即可求得预测时域内的状态量输出Y,且这种映射关系是线性的,即通过定义新的状态量将非线性系统线性化。

类似地,定义优化目标函数:

(33)

仿真及实验的理想控制效果为车辆运行轨迹和目标轨迹重合,因此Yref=[0,0,…,0]T。结合式(32)和式(33),优化函数可以改写为:

J(k)=ΔUT(ΘTQΘ+R)ΔU+2ETQΘΔU+ρε2+ETQE

(34)

将ΔU作为参数,则上述目标函数转变为quadprog二次规划问题,将优化后的结果序列ΔU中的第一个元素作用于被控对象,在下一时刻重复上述步骤,即可实现模型预测控制。由于二次规划问题已有较为完备高效的求解方法,因此该模型计算速度较快,在实际应用中可以结合PID辅助控制,使车辆尽量在纵向上实现恒速行驶。

3.4 控制器MATLAB仿真验证

在MATLAB中对上述两种模型进行仿真验证,待跟踪的轨迹由轨迹规划给出。仿真时,对于同一条参考轨迹,为比较两种方法的控制效果,在同样仿真参数下进行验证,具体数值见表1。非线性模型预测仿真中,目标函数权重设置为:R=Q=100INp;线性模型预测仿真中,目标函数权重设置为:R=Q=100INp,PID控制器参数为:Kp=0.5,Ki=0.08,Kd=0.01。

表1 模型预测控制仿真参数

结合动力学模型约束条件及履带车本身机械结构、稳定性要求,对模型预测控制的控制量、控制量增量及状态量进行约束,边界条件见表2。

表2 模型预测控制仿真约束

设定履带与待施工路面间的最小安全距离为0.2 m,步进距离为6 m,则履带车在终点的位置目标状态为[xend,yend,φend]=[6,0,0],理想状态下履带车纵向速度恒定为1 m。假设车辆初始位姿为[x0,y0,φ0]=[0,0.5,0],取优化函数中曲率及急动度的采样步长均为0.1 m,优化函数的权重系数分别为:at=bt=1(t∈[1,60]),ct=100,优化算法采用内点法。四次多项式轨迹规划输出结果为:

y=-0.0012x4+0.0185x3-0.0833x2+0.5

(35)

终点处曲率为1.3×10-4,横摆角为1.4×10-12,履带车几何中心纵坐标为2.12×10-12,轨迹最大曲率为0.16,可见该轨迹规划满足轨迹平稳及终点运动状态要求。

在上述参考轨迹及约束条件下,在MATLAB中对非线性模型预测控制、线性模型预测控制与PID控制耦合模型分别进行仿真,得到图9所示结果。

图9 模型预测结果图

从结果图可以看出,在理想条件下,非线性模型预测控制和线性模型预测与PID耦合控制均能对给定轨迹进行较精确的跟踪。

为进一步分析两种算法的优劣,对整个仿真过程中的状态量及其偏差进行分析,绘制出运动学参数相对于纵向位置的变化图,如图10所示。

图10 模型预测结果分析图

上述两种工况下,线性模型预测的线速度曲线起初对轨迹速度的跟踪效果较差,但随着仿真的进行,其线速度偏差逐渐回落,最后趋于平稳,其后半程偏差均稳定在0.01 m/s内,这是由于在控制算法中加入了PID横向速度跟踪控制器,其对线速度和角速度的跟踪性能远强于非线性模型预测控制器。

值得注意的是,线性模型预测控制器的纵向位置偏差均较高,但总体跟踪效果仍良好,这说明该控制算法对横向位置的跟踪有延迟性,但随着时间的推移,控制算法能较快弥补,且接近终点处该算法的各项参数均更加稳定,说明该算法在终点处控制效果更好。两种算法的横向位置偏差均远小于0.2 m,说明轨迹跟踪满足碰撞极限约束。

4 结论

本文针对道面摊铺后处理智能车,设计了一种基于MPC的步进行驶控制器,相较于人工步进行驶,该控制器基于履带车动力学模型、四次多项式轨迹规划及MPC控制算法实现了自动的步进行驶,提高了行驶的安全性及终点的平稳性。在MATLAB中对上述控制器进行仿真验证,结果表明,本文设计的控制器满足功能要求,对提升道面后处理施工效率具有重要意义。