可逆地铁风机用翼型优化设计与验证*

高一鸣,张 森▲,方浩楠,郑玉宙,谭兴国,2

(1.河南理工大学 机械与动力工程学院,河南 焦作 454003;2．哈密职业技术学院 机电系,新疆 哈密 839001)

0 引言

城市地铁交通是解决大型城市公共交通的主要途径,目前在我国正在大力发展[1]。由于地铁交通用于日常通风和消防排烟的需求,作为地铁通风系统中关键设备的地铁风机也开始了大规模的应用和发展,与传统的单向风机不同,地铁风机要求完全可逆[2]。作为叶片设计的基本组成单元,可逆翼型的选取对整机性能的影响起着重要的作用[3],因此,广大学者针对可逆翼型的设计进行了大量的研究工作。

李超俊等[4]率先提出了一种由原始翼型相同的两个机翼翼型反向对接形成的一种反向对称翼型,并对模型风机进行实验,结果表明该风机正、反风性能基本相同。席德科等[5]针对可逆风机的使用条件,提出了一种寻找可逆风机用的可逆翼型的方法,并对其可靠性进行了验证。王晓航[6]使用NACA0010-NACA0030翼型族作为初始翼型,以最大厚度位置为分界线,取前缘部分进行镜像拼接,最终得到可逆翼型。除了反向拼接得到可逆翼型外,还有部分学者通过设计“S”型中弧线来获得“S”型可逆翼型。黄典贵[7]采用公式对中弧线进行设计,并将基于NACA 4位数系列翼型反向搭接得到的“S”型可逆翼型厚度分布布置在设计的中弧线上,从而得出所需要的S型可逆翼型。Chacko等[8]采用同样的设计方法构造出“S”型可逆翼型,并对3种不同厚度分布的“S”型翼型进行实验研究,最终得到最大厚度在30%弦长处的叶轮性能最佳的结果。

对于不同形式的可逆翼型,国内外专家学者都进行了大量的研究工作,提出了多种可逆翼型的设计方法。然而,目前的设计方法自由度较小,人为影响因素较大,具有一定的局限性。因此本文选取性能较好的R18可逆翼型作为初始翼型,通过翼型优化方法得到一款优化翼型,利用数值模拟以及与试验结果对比的方法来验证翼型优化设计方法的可靠性。

1 可逆翼型气动优化设计

1.1 优化设计方法

由于优化翼型为完全对称翼型,翼型轮廓关于弦线和弦线中点完全对称,鉴于此特点,只需对四分之一曲线进行参数化,因此本文利用6控制点5阶Bezier多项式对完全对称翼型进行表达的参数化设计方法,既能获得较高拟合精度,又能够主动控制翼型型线设计参数,贝塞尔曲线的控制点坐标如式(1)和式(2)所示。

(1)

(2)

式中:X和Y分别为控制点的横坐标和纵坐标;T为翼型的最大相对厚度;kXi和kYi分别为横纵坐标控制系数,其中kXi∈(0,1),kYi∈(0,1),采用上述设计方法对翼型型线进行构造,翼型轮廓如图1所示。

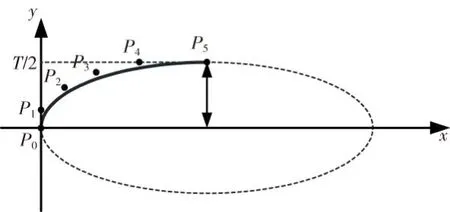
图1 完全对称翼型的参数化表达

由于翼型参数化设计方法中出现了6个设计变量,具有较大的设计空间,很难人为选择出最优的翼型,鉴于此,本文通过Fortran语言编写上述翼型参数化设计程序代码,并将ICEM网格划分和Fluent流场仿真集成起来,利用MIGA算法对相应的目标函数进行求解,实现了完全对称翼型的优化设计,优化流程如图2所示。

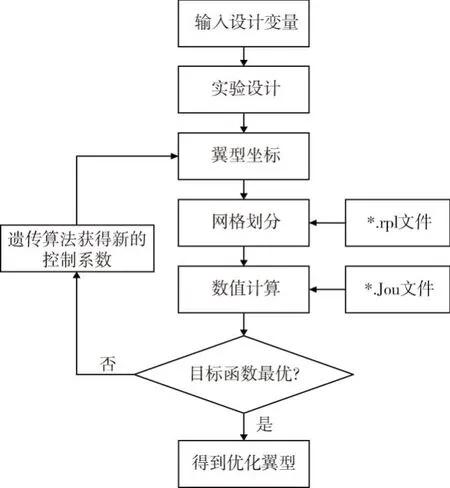
图2 优化流程

将设计攻角处的升阻比作为设计目标,针对不同设计攻角,分别给予相应的权重值,最终将完全对称翼型的优化设计转化为单目标优化问题,目标函数如式(3)所示。

(3)

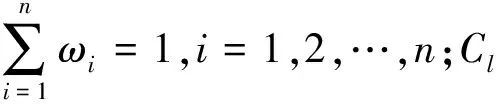
1.2 翼型气动特性数值模拟方法

Fluent软件将不同领域的计算软件组合起来,对于数值问题的计算速度、稳定性和精度等方面都有非常理想的结果[9]。熊莉芳等[10]应用k-ε两方程模型通过对某管道湍流稳态的模拟并与理论分析比较,结果证明,k-ε湍流模型对于内部的稳态或非稳态的充分发展湍流都很适用。李文华和苏明军[11]选用S-A湍流模型和k-ε湍流模型对有壁面边界的空气流动进行计算,结果显示S-A模型比k-ε模型更易收敛,并为分析风力机翼型气动特性提供了一个较好的湍流模型。

在进行数值模拟时,不同的数值模拟技术具有不同的适用范围和精度,现阶段还没有找到对所有数值模拟都很好的湍流模型。对于数值仿真的计算情况来说,湍流模型只要能够满足一定的精度要求、占用计算资源少、计算时间短,就可以用于数值计算,本文拟选取S-A湍流模型对翼型进行计算求解。

1.3 结果与分析

以可逆翼型中性能较好的R18翼型为基础对象,采用本文的翼型设计方法对R18翼型进行优化,给定设计状态为v=15 m/s,Re=1×106,在保证翼型最大相对厚度不变的情况下,设计攻角选择位于升力系数曲线的线性段,选取3°和6°攻角,并取权重值ωi=0.5(i=1,2),进行600步迭代计算。优化后控制系数结果如表1所示。

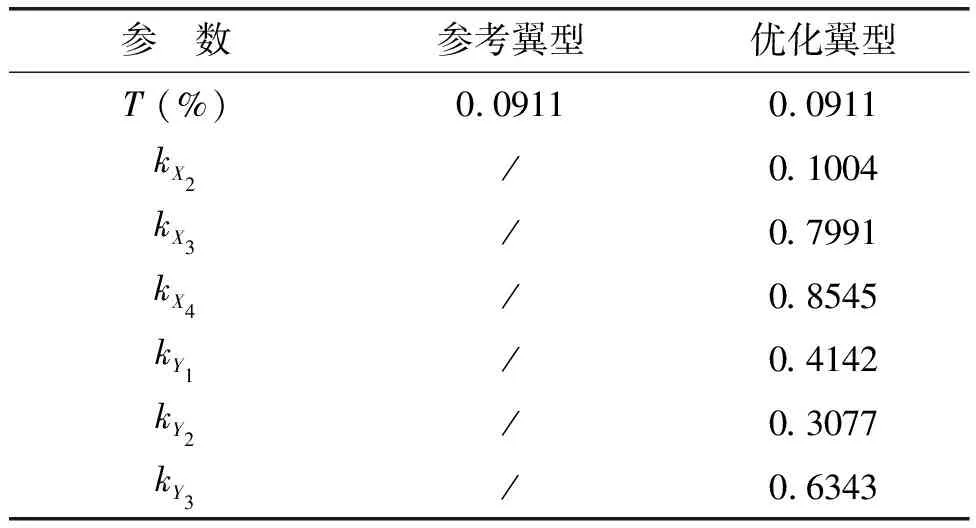
表1 优化结果

优化设计后得到的完全对称翼型型线如图3所示。

图3 优化翼型轮廓图

图4中给出了优化翼型和参考翼型在不同攻角下的气动性能比较,从图4(a)中还可以看出,在α∈[0°,8°]攻角范围内,优化翼型的升力特性均优于参考翼型,且随着攻角的增加,差距越明显。此外,如图4(b)所示,在α∈[0°,8°]攻角范围内,随着攻角的增加,优化翼型的升阻比特性也表现出了显著提升。

图4 气动性能对比曲线

2 基于可逆翼型的风机数值计算

使用与实验相同的叶片扭曲规律对叶片进行构造,并在Numeca仿真软件中进行计算,将计算结果与实验数据进行对比,从而验证Numeca数值仿真能够正确预测叶轮转子的气动性能,进而用该数值仿真方法对优化翼型构建的叶轮转子进行仿真计算,与R18翼型构建的叶轮进行气动性能的比较。

2.1 数值仿真验证

参考文献[3]中R18翼型构造的可逆风机性能测试实验数据,利用实验数据对计算模型的网格无关性进行检查,通过改变流动方向、叶展方向和圆周方向的网格节点数和分布情况,得到了不同的网格节点数,然后计算得到不同工况下的气动性能,并与实验结果进行对比,如表2所示。

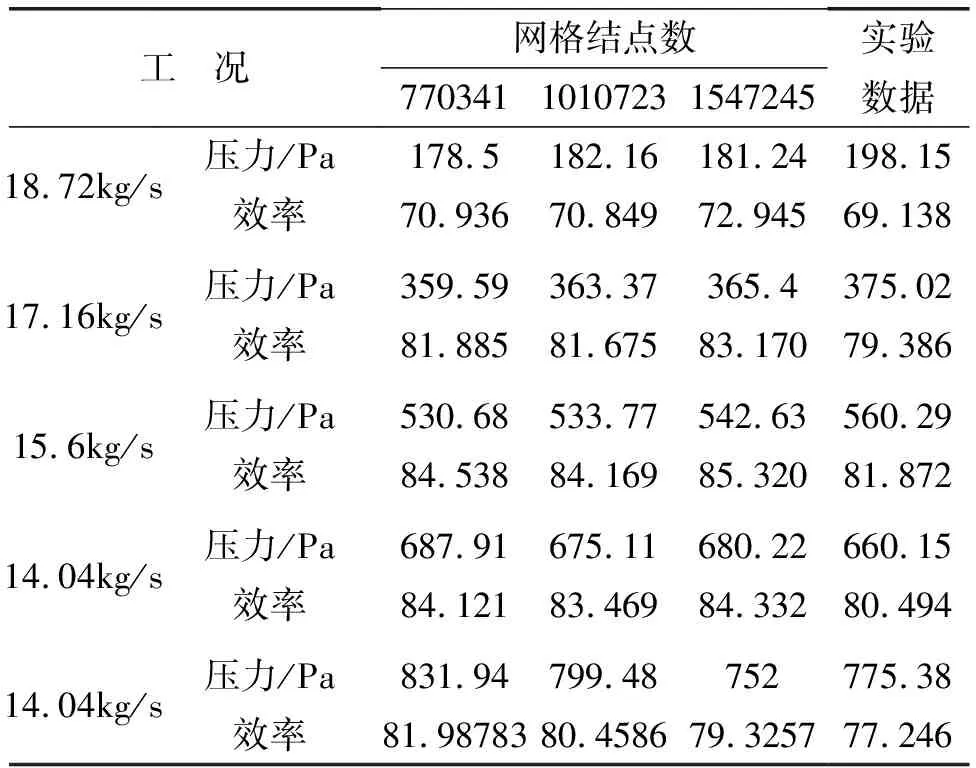
表2 不同网格数目下的气动性能比较

从表2中的总体计算结果可以看出,网格数的变化对模型的气动性能计算结果的影响很小,原因在于AutoGrid5软件对流场采用了相同的拓扑结构进行网格的划分,能够获得质量很高的结构化网格,因此网格数的多少对于计算结果的影响很小。此外,对比分析计算结果与实验数据,模型气动性能的计算结果与实验数据吻合良好,表明该计算流场能够正确预测可逆风机转子气动性能。

2.2 数值计算方法

提取R18翼型设计的可逆风机转子性能测试数据,其中转子的几何参数数据如表3所示。

表3 转子几何参数数据

通过调整设计参数使得本文中翼型设计出的叶片具有相同的弦长和安装角变化规律,叶根和叶梢的安装角分别为38°和20.3°,叶根和叶梢弦长分别为154.4 mm和136.5 mm。将叶片截面从叶根到叶梢分成7个截面,叶片造型如图5所示。

图5 叶片造型图

综合考虑网格数目对计算精度以及计算速度的影响,通过前处理软件AutoGrid5完成单转子的网格划分,对叶片区域进行O型网格划分,进出口使用H型网格划分,叶顶间隙部分进行蝶形网格划分,最终确定网格单元总数为1010723,其中网格节点的最小偏差角为 22.15°,最大长宽比为2212.81,最大延展比为2.93,均满足计算要求,风机总体模型如图6所示。

图6 风机整体模型

通过Fine/Turbo进行仿真计算,湍流模型采用Spalart-Allmaras模型,定解条件包括进口边界条件设置和出口边界条件设置,进口边界条件给定总压,出口边界条件给定参考压力和质量流量。叶轮中固体壁面均定义为无滑移绝热壁面,叶片以及轮毂定义为转动部件,转速为1450 rpm,其余部分均设置为静止状态。收敛残差量级设为-5.5,设计气动性能参数为:QR=13 m3/s,PR=560 Pa,分别对0.9QR、1.0QR、1.1QR以及1.2QR这四个流量点进行计算。

2.3 结果与分析

可逆风机的特性曲线是评价风机气动性能优劣的依据,对于风机气动性能而言,全压和效率是其中最为重要的指标,本节对特性曲线和压力系数曲线进行了对比分析。图7为两种翼型设计风机的全压-流量曲线和效率-流量曲线对比。

图7 气动性能对比曲线

从图7可看出,在设计工况点附近,优化翼型设计的叶轮全压始终高于R18翼型设计的叶轮全压,在0.8Q、0.9Q、1.0Q、1.1Q、1.2Q工况下,优化翼型设计叶轮的全压相比于R18翼型设计叶轮的全压分别提升了3.51%、3.72%、4.39%、6.04%、9.50%。在1.0Q、1.1Q、1.2Q工况下,优化翼型设计叶轮效率相比于R18翼型设计叶轮的效率分别增加了0.58%、1.00%、2.78%,小流量工况下优化翼型设计的叶轮效率基本与R18翼型设计的叶轮效率相同,这是由于优化翼型的阻力系数在大攻角下较大。综合对比两种叶轮的气动性能,采用优化翼型设计出的可逆风机转子具有更加优越的气动性能,不仅在全工况下具有更高的全压,而且在额定工况范围内可逆风机的效率提升较为显著。

图8为标况下两种叶片的压力云图,从图8(a)和图8(b)可以看出,优化叶片压力面整体压力略大于R18叶片,但是在最大厚度处出现明显的突降,吸力面同样存在这种现象,这与构造该叶片的翼型有关,为探索产生该现象的原因,图9给出了两种叶片不同叶高的压力系数。

图8 叶片压力云图

图9 不同叶高压力系数对比图

图9给出了两种叶片在10%叶高、50%叶高以及90%叶高处的压力系数对比,可以看出,在10%叶高处R18叶片的表面载荷低于优化叶片,说明其在叶根处做功能力较弱,容易导致在根部的流动损失较大。而优化叶片根部的载荷较大,提升了叶根处的做功能力,并延缓了叶根处角区分离的出现。随着叶高的增加,优化翼型设计叶片的压力系数相比于R18翼型设计叶片的压力系数仍增长明显,但是在叶片最大相对厚度附近,优化翼型设计叶片压力系数迅速降低,这是因为优化翼型设计叶片最大相对厚度附近曲率变大,气流流经此处离心力变大,从而导致压力系数下降,这与图8中优化翼型设计叶片的压力云图特征相符。

3 结论

1)采用Fortran语言编写完全对称翼型参数化设计程序代码,并与ICEM网格划分和Fluent数值仿真集成起来,借助MIGA算法实现了完全对称翼型的自动优化设计。

2)以地铁风机用R18翼型为参考翼型进行优化设计,通过Numeca进行叶轮设计并进行数值模拟验证。设计叶片过程中,使其具有和实验数据相同的扭曲规律和工作环境,对比实验结果和数值仿真结果显示,采用Numeca数值仿真软件能够正确预测三维叶片气动性能。

3)对R18翼型进行优化设计,得出与R18翼型具有相同最大相对厚度的优化翼型,按同等扭曲设计叶片并进行气动性能计算。计算结果显示,相较于R18翼型设计出的风机,优化翼型设计出的风机全压提升5.43%,效率提升0.905%,设计完全对称翼型优化方法能够有效提升翼型和转子的气动性能。