基于参数敏感性的拉伸夹具响应面优化*

陈 鑫,寇会贤,刁东明,李品豫,林明明,宁惠君

(河南科技大学 土木建筑学院,河南 洛阳 471000)

0 引言

新材料的发展突飞猛进,新型复合材料在各领域起着越来越重要的作用,且随着时代的需求,有着向轻薄型方向发展的趋势。但目前针对轻薄型材料的力学性能拉伸实验中,传统拉伸夹具存在拉伸夹持力不足、试件滑移、无法精确定位等问题。

对于夹具的结构设计,王霆[1]等人针对万能材料试验机传统拉伸夹具的结构、夹持方式等方面进行改进,研制出一种新型主动式内外夹紧力恒定的夹具。邢承亮[2]等人根据金属丝的结构特点设计了专门用于金属丝拉伸性能测试的夹具。目前针对拉伸夹具设计的研究多集中在针对特定试件类型以及特定使用环境[3-5]。在多学科交叉环境下,计算机仿真的应用在夹具结构优化中成为越来越广泛的应用,张智森[6]等人基于 UG 三维软件进行夹具的实体建模,并利用 ANSYS 有限元软件对其进行了模态分析,针对夹具的固有频率、振型和响应位移等仿真数据对其缺陷进行了分析,并据此对其进行了结构优化。王亮[7]等人通过有限元的方法分析夹具最大变形区位置,在最大变形区附近设计增强结构来减小变形、提高结构刚性。刘伟[8]等人设计研发了一款包含可胀心轴、油缸卡爪、气密性检测的全自动化智能卧试加工夹具,并对其进行了理论分析和有限元仿真分析。然而,针对拉伸夹具的优化设计,在结构参数化方面的研究则不足。

本文探讨了轻薄型材料在力学性能拉伸试验中,传统拉伸夹具所存在的问题,如拉伸加持力不足、试件滑移、无法精确定位等,并提出了一种双夹层结构拉伸夹具,该夹具具有可定位功能,可以有效解决以上问题。同时,本文还采用了有限元仿真和响应面法(RSM)相结合的方法对拉伸夹具的连接结构进行了优化设计,得到了拉伸夹具结构的最优模型,从而有效降低了结构的等效应力以及总变形。

1 可定位双夹层拉伸夹具的工作原理

从图1中可以看出,可定位双夹层拉伸装置整体被分成两个部件:外夹装置和内夹装置。外夹装置由外夹固定块、外夹连接头和两个外夹板构成,内夹装置由内夹固定块与两个内夹片构成[9]。

图1 拉伸夹具总体结构示意图

在测试样品的拉力测试中,将外部夹具的外夹连接头连接到测试载荷装置上。在此基础上,将试验样品置于两块内部板片间,并依据内部板片上垂直定位标尺对其被夹持部位的长度进行调节。然后转动内部夹持器的转子,使两块内部夹持器的夹持器闭合,并将试样预先固定。最后,将外部夹持转子转动至两块外部夹持两块内部夹持,在保证试样被夹持后,就可以进行抗拉测试了。

2 可定位双夹层拉伸夹具的静力学分析

2.1 简化有限元模型

为了降低分析的复杂程度,并减小计算的工作量,对可定位双层拉伸夹具的结构进行了简化[10],简化结果如图2所示。

图2 拉伸夹具简化模型

2.2 拉伸试验仿真模拟

在保证计算精度的前提下,本文采用局部网格加密的方式以优化计算时间。在考虑拉伸测试的真实情况时,本文采用了绑定接触来连接相互焊接的部件,并将相互接触的部分设置为摩擦接触。在内外夹板的配合处,则采用了无分离接触。此外,对外夹连接头施加了固定约束,并对拉伸试件的下表面施加了竖直向下的1000 N力载荷。同时,本文还对外夹板的表面施加了水平位移约束,以保证夹具加持状态。

夹具网格划分以及边界条件设置结果如图3、图4所示。

图3 网格划分

夹具仿真计算结果如图5、图6所示。

图5 夹具等效应力云图

由图可知,夹具整体结构等效应力最大处为外夹固定块与外夹板间的连接结构处,最大应力值为50.583 MPa,最大总变形处为外夹板以及连接构件处,总变形值为0.0044 mm。

3 可定位双夹层拉伸夹具的优化设计

根据数值模拟结果,夹具最大等效应力位置在外夹固定块与外夹板间的连接结构处,由于连接结构是整个夹具的主要受力部位,因此,连接结构的设计是否恰当,直接关系到整个夹具的安全与可靠。因此,为了提高连接结构的强度与刚度,应用响应面法对拉伸夹具连接结构进行了优化设计[11]。

3.1 结构参数化

对内夹固定块与内夹板间和外夹固定块与外夹板之间的连接结构进行参数化建模,具体的优化参数参见图7、图8。

图7 内夹连接结构横截面优化参数

图8 外夹连接结构横截面优化参数

优化变量的原始值以及可变幅度如表1所示。

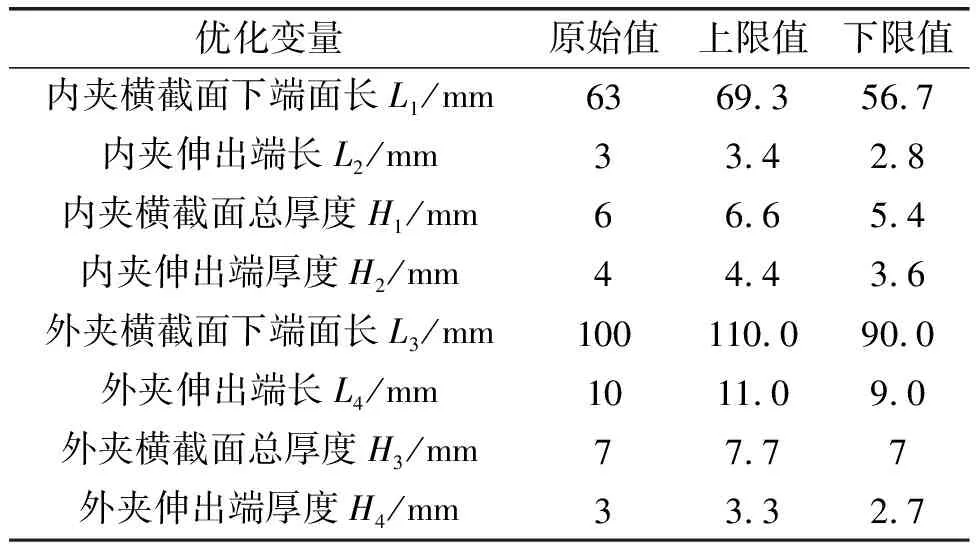
表1 连接结构的几何尺寸

3.2 敏感性分析

敏感性分析是通过量化的方式,来探讨在有关因子改变时,各主要因子对各因子的作用大小。其本质就是用渐进式的方式,来说明各因子对各因子的影响所产生的影响。主要指数的重要性是由输入与输出的相关性决定的。

在有限元分析中,可以利用局域敏感性来衡量输入参数对输出量的影响。为了研究连接结构的8个尺寸参数(表1)对最大等效应力P19和最大总变形量P20的影响,利用斯皮尔曼分级相关系数方法精确计算尺寸参数对目标函数的灵敏度,敏感性分析结果如图9所示[12]。

图9 各变量敏感性分析结果

由图9中的部分灵敏度分析结果可知,L4、L3、H3、H4对双夹层拉伸夹具结构的最大等效应力的影响是最显著的。而且在响应点附近,L4和L3产生正影响,H3和H4产生负影响,其作用效果从大到小为L3>H3>L4>H4。与此同时,在响应点的局部范围内,对于结构最大总变形,L4和L3的影响程度远大于其余变量,并且作用效果L3>L4。

3.3 响应面建立

从灵敏性分析可以看出,对双夹层拉伸夹具结构最大等效应力和最大总变形产生影响的主要变量是L4、L3、H4、H3。所以,为了提高计算效率,只选择上述4个变量作为输入变量,而输出变量不变。

图10-图13是在响应面模组中所得到的三维响应曲面,其设计目标随着不同的设计参数而改变。

图10 等效应力随L3和H3变化的响应曲面

图11 等效应力随L3和H4变化的响应曲面

图12 总变形随L3和H3变化的响应曲面

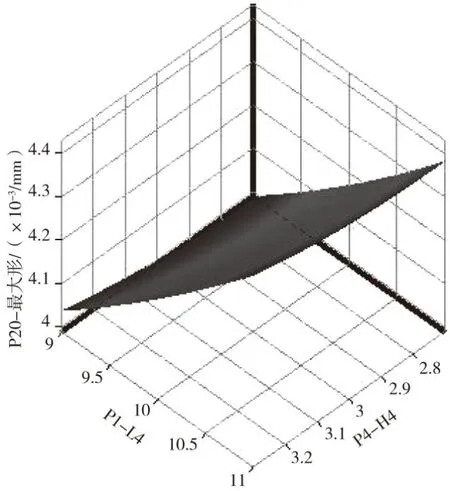
图13 总变形随L4和H4变化的响应曲面

3.4 优化结果

在响应曲面优化模块中,以影响连接结构强度的主要因素:外夹横截面下端面长、外夹伸出端长、外夹横截面总厚度、外夹伸出端厚度为设计变量,以结构的最大等效应力和最大总变形的最小值为优化目标,选择MOGA算法进行优化求解,最终得到3组候选点,如表2所示。

表2 响应面优化结果

候选点的有限元计算结果如表3所示。

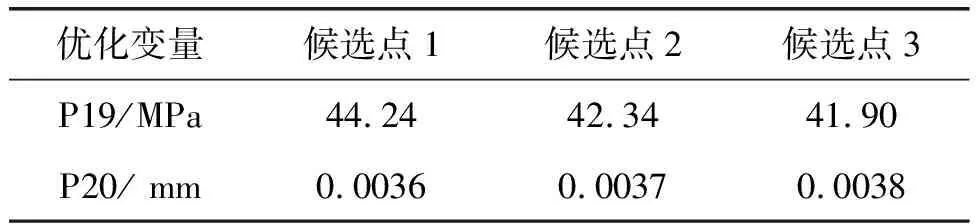
表3 候选点有限元计算结果

选取候选点3为最优模型,对比初始模型有限元仿真计算结果可知,优化后的拉伸夹具连接构件的最大等效应力下降了17.2%,最大总变形减少13.6%。

4 结论

通过简化建模和静力学分析,得知可定位双夹层拉伸夹具最大变形和最大等效应力均在外夹固定块与外夹板间的连接结构处,分别为0.0044 mm和50.583 MPa。为了提高连接结构的强度与刚度,并优化拉伸夹具装置的结构组成,本研究将影响内外夹连接结构强度的主要因素作为变量,以结构的最大等效应力和最大总变形的最小值为优化目标,对拉伸夹具进行参数化建模和响应面优化分析。通过Optimal Space-Filling Design,在该空间上实现了样本点的平均生成,利用神经网络建立了响应面,并应用OMGA算法对8000个原始样本点进行筛选以获取最佳设计点。最终,本研究实现了在拉伸夹具等效应力下降17.2%以及整体变形下降13.6%的优化效果,这一结果具有显著的实际价值,可以有效地节约研发和实验成本。此外,本研究还为多目标夹具设计等领域提供了有益的参考,具有广泛的学术借鉴意义。