高速动车组车体整备垂弯频率优化研究

李娅娜,史鑫鹏,刘靖楠

(大连交通大学 机车车辆工程学院,辽宁 大连 116028)

随着我国高速铁路运行里程的不断增加,高速动车组技术发展也越来越快,设计者越来越重视车体的轻量化设计。轻量化设计的同时也带来了诸多问题,如车体弯曲刚度下降、固有频率降低等。固有频率的降低会使车体更易受到外界激扰而与车下设备产生共振,影响乘坐舒适性及使用寿命等。因此,在对车体进行设计时要同时保证其刚度、强度及模态,以提高乘坐舒适性。

目前,有关提高高速列车模态频率的方法主要有基于尺寸优化法优化板厚参数、基于应变能法优化结构、基于设备吊挂方式优化吊挂参数以及采用新材料等。Cho等[1]在对铝材动车组进行轻量化设计的同时考虑了车体一阶垂弯频率。Dumitriu等[2]研究发现,悬架及车下设备的刚度对车体的弯曲频率有较大的影响。Melero等[3]在研究轻量化的同时增加弹性贴片以提高结构阻尼,使固有频率能够小幅度降低,从而减少对舒适性的影响。高月华等[4]用灵敏度分析法对高速列车进行轻量化设计,优化后大大减轻车体质量,但一阶垂弯频率略有降低。尤泰文等[5]分别对结构参数和悬挂参数进行优化,发现悬挂参数对一阶垂弯影响更大。陶斯嘉[6]用灵敏度分析法对车体进行轻量化设计,优化后达到了车体减重的目的,同时车体各阶频率几乎不变。张军等[7]建立动车组车体有限元模型,用灵敏度分析法改变车体结构参数以提高车体固有频率,研究表明车体一阶垂弯频率有少量提高。王洋洋等[8]用自适应响应面法对车下设备悬挂参数进行优化,提高了车体的一阶垂弯频率。汤劲松等[9]采用应变能法优化车体垂弯频率,结果表明车体一阶垂弯频率略有提高。吴煜威[10]对某客车车体结构进行了轻量化设计,发现车体达到减重目标但车体模态频率略微下降。

以上研究内容大多以优化车体结构参数和改变设备吊挂方式为主。基于结构参数的优化往往会产生其他问题,模态频率的提高会带来整车质量的增加,车体的强度、刚度也会发生变化,因此,在对结构参数优化时还需要考虑多种因素。改变车下设备吊挂方式,以弹性吊挂代替刚性吊挂来提高车体垂弯频率的方法较为明显,但也要对弹性元件设置合适的刚度参数以达到最好的效果。

本文针对某高速动车组车体一阶垂弯频率较低的现象,将模态灵敏度分析和模态响应面分析方法分别应用于车体部件厚度优化和弹性元件刚度参数优化,对比分析2种优化方法的计算结果,研究其各自优缺点,从而为有效提高整备一阶垂弯频率提供技术支持。

1 基本理论及方法

1.1 模态灵敏度分析

模态灵敏度分析是研究构件固有频率随构件参数变化的有效方法[11]。与其他方法相比,模态灵敏度分析能从众多设计变量中筛选出重要的设计变量进行下一步分析。通常,车体i阶模态的固有频率ωi和振型向量ui的有限元方程为:

(1)

式中:K、M分别刚度矩阵和质量矩阵。

对式(1)求偏导可得:

(2)

整理式(2)可得:

(3)

式中:xi为设计变量。

对式(1)、式(2)化解计算可以得到第i阶固有频率对第j个设计变量的模态灵敏度:

(4)

将关系式ω=2πf代入式(4)可得:

(5)

式中:fi为车体模态频率;si为车体第i阶模态频率对第i个设计变量的模态灵敏度。

1.2 模态响应面分析

模态响应面分析法的基本思想是用一种拟合的近似数学模型来表达隐式函数[12]。响应面分析需要用自变量与因变量构造隐式函数,并以响应面的方式进行显示表达,这样更能有效解释模型,并能克服其他方法中解释性差、不直观等问题。分析中将一阶垂弯频率作为因变量,将弹性元件刚度作为自变量,通过响应面研究一阶垂弯频率与弹性元件刚度的关系,形成模态的响应面分析。

本文采用线性二阶多项式构建响应面模型:

(6)

式中:f(x)为整备状态下车体的一阶垂弯频率;xi为不同弹性元件的刚度;ci为回归系数;ε为随机误差。

1.3 整备垂弯频率求解方法

在实际情况中,车体形变很小,因此在研究带有悬挂设备的车体频率时,可将其等效为二自由度垂向模型[13],见图1。

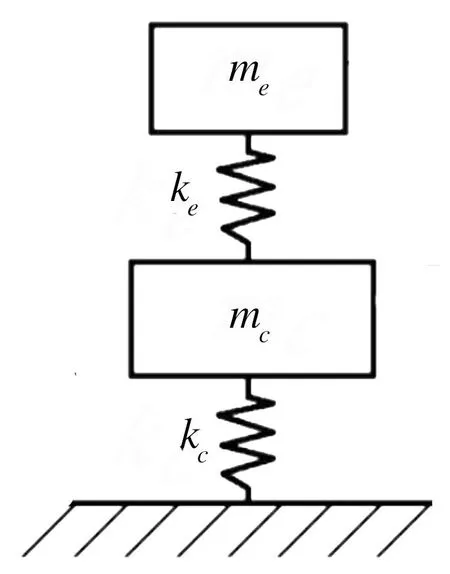
图1 二自由度垂向等效模型

根据图1所示等效模型,可求得耦合系统高频振动频率ω1和低频振动频率ω2:

(7)

(8)

式中:ke为车下设备悬挂元件刚度;me为车下设备质量;mc为车体质量;kc为车体弯曲刚度。

车下设备为弹性吊挂时,车体与车下设备的振动由ω1和ω2叠加而成[14]。在弹性元件刚度较低时,低频振动与高频振动频率均较低,低频振动频率趋于0 Hz,高频振动频率趋于整备一阶垂弯频率,此时车体一阶垂弯频率将表现为高频振动频率;在弹性元件刚度较高甚至设备与车体刚性连接时,低频振动频率趋于设备刚性连接时车体一阶垂弯频率,高频振动频率会非常大,此时车体一阶垂弯频率将表现为低频振动频率。因此,在设备与车并设置合理的刚度参数会提高垂弯频率。

2 有限元模型的建立与分析

2.1 有限元建模

本文研究的某高速轨道车辆车体由端墙、侧墙、底架、车顶和牵枕缓五大部分组成。为综合考虑质量分布对车体模态的影响,车辆整备模型(37.0 t)采用精细建模,全部设备按照具体位置进行布置。车上设备及内饰按质量重心刚性连接于各吊挂点上;车下设备采用弹性元件悬挂于边梁上。整体有限元模型见图2。

图2 整体有限元模型

车下设备除牵引变流器和污水箱外,其他设备吊点的橡胶刚度相同,具体吊点的橡胶刚度参数见表1。

表1 车下各设备吊点的橡胶刚度 N/mm

2.2 车体分析计算

对车体有限元模型分别进行刚度、静强度和整备状态模态分析。根据车体设计要求并参考BS EN 12663-1:2010+A1:2014,选取2种危险工况(垂向超员载荷工况和垂向超员+纵向压缩1 500 kN载荷工况)对车体进行刚度和静强度分析。通过分析,车体中部边梁下翼缘的垂向位移为9.27 mm,小于车辆定距17 000 mm的千分之一,符合刚度标准;车体应力最大值发生在车钩座处,数值为186 MPa,小于铝材的屈服强度215 MPa,满足强度要求。车体一阶垂弯模态振型见图3,其频率值为8.2 Hz。

3 基于尺寸参数优化车体一阶垂弯

车体的垂弯频率与车体质量和刚度有关,因此,可以通过改变车体各个部件厚度来调整车体质量与刚度,以提高车体垂弯频率。由于车体部件较多,对所有部件进行优化工作量极大,基于此本节对车体进行灵敏度分析并筛选符合要求的部件进行优化。研究表明,一般情况下车体质量与一阶垂弯频率会同时提高[15]。为了避免厚度变化引起车体质量的大幅提高,本文以不同部位板件厚度为变量,分别进行一阶垂弯频率对板厚以及质量对板厚的灵敏度分析。根据车体结构,将整车分为20个变量组,其中17个变量组以板件厚度划分,而车钩座组、牵枕缓组以及边梁组三部分以整体划分,各组内板件厚度等比例放大或减小。

在灵敏度分析中,相对灵敏度R的计算公式为:

R=sf/sm

(9)

式中:sf为模态灵敏度;sm为质量灵敏度。

灵敏度分析结果见表2。

表2 灵敏度分析

通过灵敏度分析,对相对灵敏度较高和较低的变量组进行进一步分析,前者是为了提高垂弯频率,后者是为了尽量减小车体质量的增加。选取符合上述要求的8个变量组进行厚度尺寸优化。优化结果见表3。

表3 优化结果

表3可知,优化后在车体垂弯频率增加的同时车体的质量也有增加。最终,车体垂弯频率从8.2 Hz提升至8.6 Hz,车体质量由37.0 t提升至37.5 t,垂弯频率提高不明显且车体质量增加不满足轻量化要求。因而,研究能够提高车体垂弯频率且不增加质量的方法更为重要。

4 基于刚度参数优化车体一阶垂弯

合理选择弹性吊挂的方式以及刚度参数可以提高车体的垂弯频率,因此,本节将优化弹性元件的刚度参数以提高垂弯频率。

按照隔振理论,在底架设备的各个吊点处采用橡胶作为隔振元件,设置横向、纵向和垂向三个方向的刚度。由于纵向刚度及横向刚度对垂弯频率影响较小,本次分析中只取垂向刚度作为研究对象。根据吊挂设备的质量,将弹性元件分为三组,牵引变流器的弹性元件为A组,污水箱弹性元件为B组,制动风缸和废排弹性单元为C组。除上述吊挂设备外其余的设备质量较小,对车体垂弯频率影响较小,因此不参与弹性元件刚度优化。

弹性单元的刚度可表示为:

(10)

式中:kd为设备的吊挂刚度;fd为设备的自振频率;md为吊挂设备的质量。

根据TB/T 1335—1996[16]及国际铁路联盟UIC[17]要求,整备状态车体弯曲频率不得低于10 Hz,且该值与转向架点头、沉浮频率比须大于1.414。因此,车体一阶垂弯频率要在10 Hz以上,同时,为了避免共振,车下悬挂设备的自振频率需低于7 Hz。本次优化选取A、B、C三组刚度作为设计变量,设置设备自振频率为5～7 Hz,根据式(10)求出各组弹性元件刚度上下限变化范围(表4)。A、B、C三组均由多个弹性元件组成,同组内弹性元件刚度相同。由于设计变量仅有三组刚度参数,不适用于模态灵敏度优化,本节没有采用灵敏度分析进行设计变量的筛选,而是根据Box-Behnken[18]试验原理进行正交试验设计并计算样本空间点对应的车体垂向弯曲,正交试验设计及结果见表5。

表4 弹性元件刚度范围 N/mm

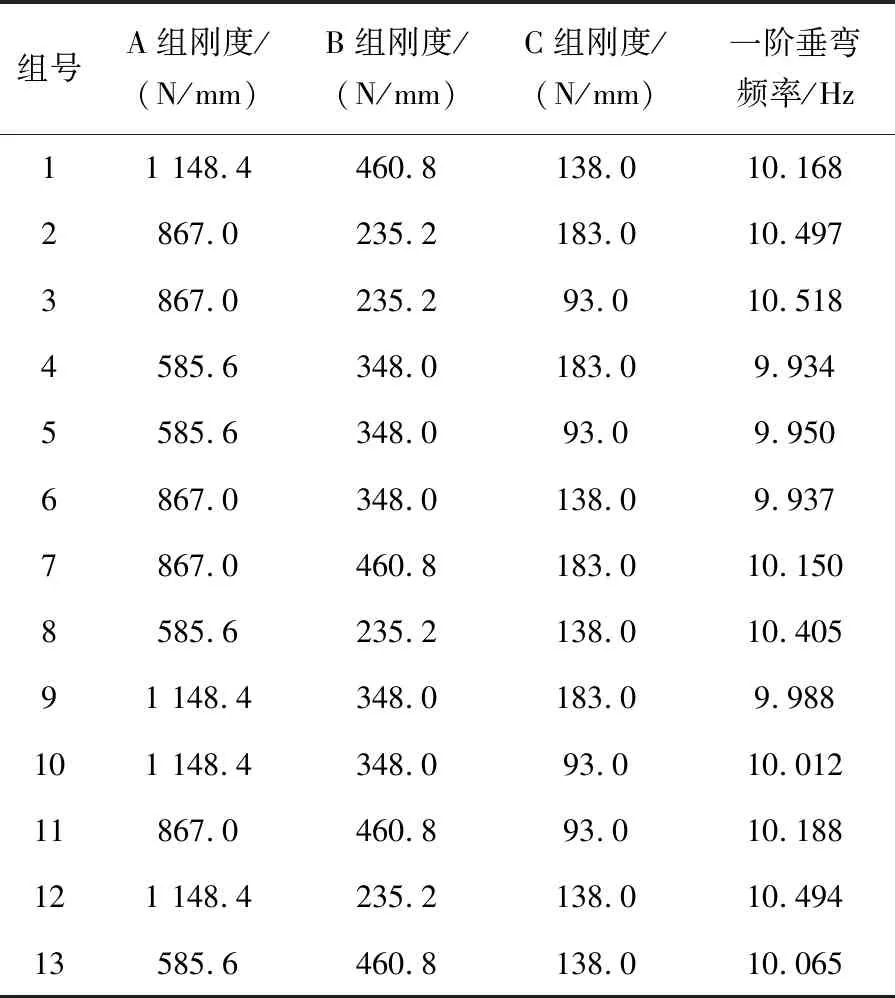
表5 正交试验设计及结果

多项式响应面模型因计算过程简单、计算时间短、优化效率高被广泛应用,鉴于此处不适合使用灵敏度优化,故选择响应面对刚度参数进行优化。

将频率拟合成关于弹性元件刚度的二次多项式:

(11)

式中:f(x)为车体一阶垂弯频率;x1、x2、x3分别为A、B、C的吊挂刚度。

根据式(11)绘制一阶垂弯的响应曲面,见图4。从图4可知,随着A组刚度的增大,车体一阶垂弯频率明显增大;随着B组刚度的增大,车体一阶垂弯频率先减后增;随着C组刚度的增大,车体一阶垂弯频率先减后增,但变动幅度不大。因此对于A组刚度参数,其刚度值接近上限会提高一阶垂弯频率,对于B组刚度参数,刚度值较低时出现频率最大值,对于C组刚度参数,其影响较小,故刚度参数基本不变。

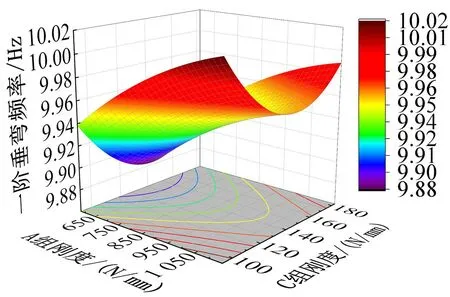
(a) A-C组弹性元件

对A、B、C三组刚度值取整,并进行模态分析,最终确定A组刚度优化为1 150 N/mm、B组刚度优化为230 N/mm、C组刚度优化为180 N/mm。将上述结果重新计算可得,车体一阶垂弯频率为10.5 Hz(大于10 Hz),满足模态匹配理论。对弹性元件刚度进行优化可以极大提高车体一阶垂弯频率,同时,由于更改的是车体与吊挂设备间弹性元件的刚度,整车质量并不会发生变化。

5 结论

本文对整备状态车体进行垂弯频率的优化研究,使该车体满足相关弹性模态频率标准的要求。

(1)参考BS EN 12663-1:2010+A1:2014[15]对整备车体进行精细建模下的刚度和强度分析,结果表明,车体刚度小于车辆定距的千分之一,最大应力不超过屈服极限,车辆刚度和静强度均符合相关标准;对车体进行初始模态分析,车体一阶垂弯频率为8.2 Hz,小于10 Hz,不满足标准要求。

(2)以车体板件厚度参数为对象对整备状态车体进行灵敏度分析。选取相对灵敏度高和相对灵敏度低的重要部件进行优化。优化后车体一阶垂弯频率由8.2 Hz提升至8.6 Hz,提升了4.88%,但车体质量由37.0 t增加至37.5 t,提升了1.35%。基于灵敏度分析优化板件厚度参数能够在一定程度上提高车体一阶垂弯频率,但垂弯频率提高的同时质量也会增加,不利于车体轻量化,需要进一步研究。

(3)以车体与设备连接处的弹性元件刚度参数为对象进行响应面分析。根据响应面分析,优化各组弹性元件刚度参数。优化后车体一阶垂弯频率由8.2 Hz提升至10.5 Hz,提升了28.05%,同时车体质量几乎不发生变化,有效地改善了车体一阶垂弯频率。