基于CIR模型的地铁客流弹性分析

徐玉萍,侯明超

(华东交通大学 交通运输工程学院,江西 南昌 330013)

我国已迈向建设交通强国的新征程,构建与其相适应的交通系统性能是未来发展的必然要求。国内外学者认为弹性是交通系统性能在受到扰动后能快速恢复的关键[1-2]。有关弹性的研究,国内起步较晚,而国外已建立了弹性的概念框架,但未形成统一的弹性量化方法[3]。

有关弹性的定义,Bruneau等[4]提出了关于生物系统的弹性概念,认为弹性是指被破坏的性能曲线所覆盖的面积与未被破坏的曲线(常数)所覆盖的面积之比,因性能损失的部分形似三角形,这一定义又被称为弹性三角形。除此之外,Pimm[5]认为弹性是某变量因扰动而偏离平衡态到再次恢复至平衡态时的速率。英国内阁办公室(2011)认为弹性可分为“4R”,即冗余性、可靠性、抵抗性和恢复性。尽管学者们对弹性的定义不同,但大家认为弹性都具有相同的特点,即弹性被视为是一个过程量,描述了扰动前、扰动中和扰动后的过程。上述定义和其他定义也被许多学者应用于交通系统的弹性研究中[6]。

从客流角度评估系统弹性的研究中,Nogal等[7]基于动态的客流平衡分配模型,构建客流压力水平和成本水平两项指标以量化道路网络性能,并通过文献[4]中的定义确定弹性。Murray[8]将路网弹性分为适应性、机动性、安全性和恢复能力4个指标,并在用户均衡和系统最优两种交通分配模式下,讨论了两者在4个指标上的差异,其中用户均衡模型有更好的适应性和安全性,而系统最优模型有良好的机动性和恢复能力。Lima等[9]依据文献[5]的弹性定义,采用O-U过程模拟伦敦地铁一天内线路的客流变化并分析线路弹性,此外,还引入泊松过程来模拟突发的大客流变化。Zhou等[10]针对极端降雨天气,使用客流压力、方向不均衡系数等指标研究地铁客流的时空特征,与此同时将随时间变化的相对客流作为弹性曲线以量化客流弹性。Adjetey等[11]分析了扰动期间延误和载客量运营指标,借助仿真的方法研究铁路运输系统的弹性,从扰动管理计划的角度评估系统弹性。Stamos等[12]为量化极端天气(EWE)下交通运输网络的弹性,以客流在各种交通方式之间的转移量为评判标准,采用三步走的方法,即EWE发生概率、EWE影响评估以及交通方式选择的替代性来确定。

本文以文献[5]的弹性定义为基础,采用CIR模型模拟各个车站客流的演变并确定客流弹性。本文方法不仅克服了利用O-U过程模拟客流时出现负值的缺陷,还对研究内容做了进一步讨论。

1 客流弹性研究方法

1.1 CIR模型

客流在时间序列上表现出一种随机性,但在短时间内,车站的客流通常会保持在一个相对稳定的水平,即正常水平。在这一前提下,基于CIR模型[13-14]提出客流弹性指标,模型能够模拟某段时间内客流的演化过程,并且参数α作为客流弹性评价指标,反映客流受扰动影响偏离正常水平到再次恢复到正常水平的速率。

(1)

(2)

式中:Xt为某车站第t天的进站和换乘总客流;μ、σ分别为短期内客流的均值和波动率;α为客流在均值方向上的恢复速率;Wt为关于时间t的布朗运动;φ为服从标准正态分布的随机数。

CIR模型反映了客流在短期内的总体均衡,在不确定的扰动因素下,如商业活动或天气,客流可能会增加或者减少。模型中的布朗运动参数Wt可以模拟客流的不确定出行行为;波动率参数σ反映了短期内客流距离正常水平μ的程度,波动率越大,客流相对于正常水平变化越大,反之越小。实际上,客流不会一直增加或减少,这与乘客的固定出行需求或地铁运营管理等因素有关。因此,CIR模型中恢复速率α(即弹性)就描述了客流从偏离正常水平到再次回归的速率。弹性α∈(0,1),当α趋近于0时,表明客流向正常水平恢复的速率越慢;当α趋近于1时,表明恢复速率越快。利用这一特点,弹性可在不同车站之间进行比较。

1.2 模型参数估计

依据参文[15],CIR模型的转移概率密度函数近似地服从正态分布,因此, CIR模型的对数似然函数可以表示为:

(3)

a=Xt+α(μ-Xt)Δ

(4)

b=σ2XtΔ

(5)

Δ=ti+1-ti

(6)

式中:a为正态分布的均值;b为正态分布的方差;n为模拟客流的天数;Δ为时间步长。

本文采用极大似然估计CIR模型参数,利用对数似然函数分别对α、μ和σ求偏导数,可以得到:

(7)

(8)

(9)

然后,分别令式(7)～式(9)等于零,并求解方程组得到模型参数α、μ和σ。

CIR模型的模拟值具有随机性,但在多次模拟下,任意时刻的平均客流都将趋近于均值μ,结合随机种子,可以巧妙地将参数特征可视化(图1)。某地铁站在某一天的客流因扰动影响而偏离正常水平位于某较低值,其偏离程度取决于波动率σ。随着时间推移,扰动逐渐退散,客流逐渐回升并最终再次达到正常水平,而这一过程的弹性由恢复速率α表征。同理,当扰动造成客流高于正常水平时的恢复过程亦是如此。

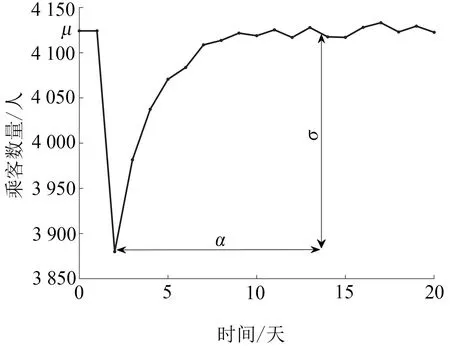
图1 参数特征

2 案例分析

2.1 车站客流弹性

本文的案例分析以南昌市地铁为例,截至2021年底,南昌市地铁有三条运营线路,70座地铁站。利用 2021年1月～7月各个车站进站和换乘客流数据来验证方法的可行性。为分析日常客流的波动行为,在数据处理时,过滤掉元旦等节日的数据点。由分析可知,有80%的车站能够在误差允许范围内通过验证。为了分析多情景下的客流弹性,车站的选择需考虑线路、位置等因素,选取地铁站中的9个车站进行说明。南昌市地铁拓扑网络见图2。

图2 南昌市地铁拓扑网络

图3展示了9个车站在短期内的客流演变。根据上一节的方法,通过式(5)～式(7)估计CIR模型中的α、μ和σ,具体数值见表1。从表1可知,长江路站和上沙沟站的弹性最高,达到0.78,表明客流在受扰动冲击后能快速恢复至正常水平;地铁大厦站的弹性最低,仅为0.37,表明客流可能在较长时间都将偏离正常水平;同时,地铁大厦站的波动率也是最大的,表明客流受扰动因素影响而变化剧烈。作为1号线和2号线的换乘站,车站之间的交换客流可能是导致客流弹性低、波动率高的原因。值得注意的是,长江路站客流的波动率约为上沙沟站的两倍,但弹性与之相同,表现出长江路站客流对扰动更加敏感。由于影响周期是短暂的,因此客流能以较快的速率恢复到正常水平。

表1 车站客流模拟结果

图3 短期客流演变

以施饶站为例分析不同参数时客流的演变过程,参数下的客流演变见图4。从图4可知,当波动率σ相同时,弹性越高客流恢复到正常水平的速率越快;当弹性α相同时,波动率越大客流变化越剧烈。

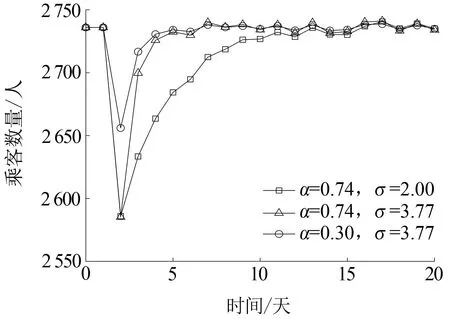
图4 参数下的客流演变

本文针对每个车站,借助Matlab编程模拟表1参数的客流演变过程。模拟过程如下:

①初始化模型参数:α、μ和σ。

②定义时间参数:时间步长为dt、模拟天数为n。

⑤模拟第i天客流Xi=Xtemp。

⑥重复④～⑤,,模拟第i+1,…,n天客流。

模拟客流以经验累积分布函数(ECDF)曲线的形式给出,见图5。结合图5数据并根据式 (8) 计算模拟客流与实际客流的平均误差,计算可知,平均误差在20%以内,且通过K-S检验,模拟值与实际值具有相同分布(P>0.05)。上述计算结果验证了客流弹性、波动率参数估计值的可靠性。

(a) 1号线1、3车站

(10)

式中:n是模拟客流的总天数;Xi是第i天的模拟客流量;Yi是第i天的实际客流量。

2.2 客流弹性影响分析

车站客流是多个车站进站和换乘客流之和,通过CIR模型模拟9个车站的客流演变,其平均误差为10.95%。同样地,可模拟其他组合车站的客流。根据多车站客流弹性与其车站的内在联系能够得到整体客流的演变规律。首先分析多车站客流弹性与其中最大客流车站的弹性关系,具体做法如下:

①计算9个车站的客流弹性以及其中最大客流车站的弹性;②去除最大客流车站,计算剩余组合车站的客流弹性以及其中最大客流车站的弹性;③重复②,直至剩余两个车站。

多车站客流与最大客流车站的弹性关系见图6。从图6可知,两者呈正相关,随着最大客流车站弹性的增大,多车站客流弹性也在增大。另外,最大客流车站主导多车站的客流弹性,如在有9个车站的多车站情况下客流弹性仅是0.45,正是因为地铁大厦站的客流弹性是0.37,远低于其他车站弹性的平均值0.71。

图6 多车站客流与最大客流车站的弹性关系

分析多车站客流弹性与其中小客流车站的关系时,将9个车站按客流量分为大客流车站和小客流车站,其中地铁大厦站为大客流车站,其余8个车站为小客流车站。在模拟客流演变时,可将8个小客流车站的客流合并作为一个整体,合并后的客流均值仍小于地铁大厦站的客流均值。假设在两类客流波动率σ相同的情况下,讨论两者的关联。

多车站与小客流车站的弹性关系见图7。从图中可知,当小客流车站的客流弹性α=0.2时,多车站客流弹性随客流均值逐渐减小,这是由于小客流所占的总客流权重增大,削弱了最大客流的主导作用,使得多车站客流弹性趋向于小客流车站的客流弹性;当小客流车站的客流弹性α=0.5时,多车站客流弹性基本不变,近似于最大客流车站(地铁大厦站)的弹性,在此情况下,多车站客流弹性依然由最大客流车站主导;当小客流车站的客流弹性α=0.8时,多车站客流弹性随客流均值的增大逐渐增大,与α=0.2时相同,多车站客流弹性受小客流车站的影响,其客流弹性有所增大。

图7 多车站与小客流车站的客流弹性关系

3 结论

(1) 通过CIR模型能够模拟稳定客流在短期时间内的波动过程,平均误差在20%以内。

(2) 客流弹性指标定量描述了地铁客流在受扰动后再次恢复到正常水平时的速率,为客流的变化规律提供一种新的量化指标。

(3) 本文研究的案例中,中间站的客流弹性平均值为0.71,波动率平均值为7.29,具有客流弹性高、波动率低的特征;地铁大厦站作为换乘站,其客流弹性为0.37,波动率为37.39,具有客流弹性低、波动率高的特征。多车站组合客流的弹性受其单一车站客流弹性的影响,即受大客流车站弹性主导,小客流车站弹性牵制。