多稳态力学超构材料研究进展
2024-03-04何玉龙孙嘉鹏卢明辉陈延峰
徐 锐,何玉龙,3,孙嘉鹏,李 鑫,卢明辉,陈延峰
(1.南京大学 现代工程与应用科学学院,江苏 南京 210093;2.南京理工大学 机械工程学院,江苏 南京 210094;3.太原理工大学 机械与运载工程学院,山西 太原 030024)
超构材料(Metamaterials,又称超材料)是人工设计制备、尺寸介于微观与宏观尺度之间、具有一定物理性能的功能基元按照特定结构空间对称性构建的微结构材料[1-5]。通过这类人工设计的特殊微结构,超构材料能实现常规材料所不具备的新颖超常的力学[6-8]、热学[9-11]、声学[12-14]和光学[3,15]性能。在这些新型的超构材料中,力学超构材料(Mechanical metamaterials,又称机械超构材料)是指基于几何微结构构建的一种具有特殊力学性能的材料[16-18],如负泊松比拉胀行为[5,19]、负热膨胀[7,20]、多稳态[21-23]、可调刚度[24]等等。多稳态力学超构材料(Multi-stable mechanical metamaterials,MMMs)是力学超构材料的一种,在外界载荷作用下可以形成多个稳态的构型且可以互逆切换[21]。多稳态力学超构材料通常由双稳态结构通过串联、并联得到[25]。双稳态结构具有两个稳定构型,当外界载荷超过稳态转变临界载荷时,结构跨越能量势垒,会从当前稳态迅速切换至第二稳态,并且无需能量持续输入即可保持该形变状态。双稳态结构的几何尺寸、结构形式和材料属性决定了能量势垒,通过参数调节可以调整其动力输出与突弹跳变阈值[23,26,27]。在自然界和日常生活中双稳态结构随处可见,如捕蝇草的叶子(“开关”与“闭合”)、蜂鸟的喙(快速闭合吞食昆虫)、开关、瓶盖、笔帽、塑料卡扣、尼龙扎带、弹跳玩具球、卷尺、发卡等等[28]。大多数自然和工程双稳态结构可按照研究对象分为3类,如图1所示:(1)梁、桁架、柔顺机构;(2)曲面和薄壳结构;(3)其他结构,如剪纸、卡扣结构等。
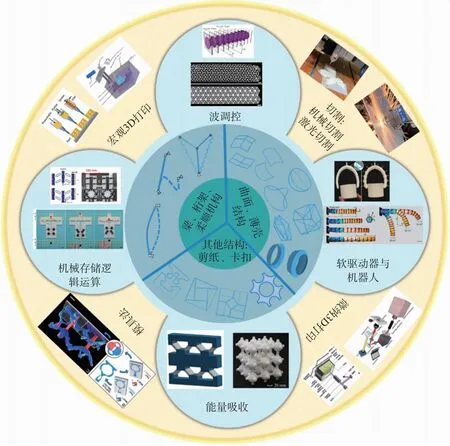
图1 双稳态单元结构和多稳态力学超构材料的应用
最近十年,双/多稳态因其优异的性能引起了研究人员的广泛关注:(1)双稳态结构可以保持变形形状,施加相反作用力可以恢复为初始状态,这种可重复使用特性提高了器件的利用率[29]。(2)双稳态结构通过塑性变形可以将能量“锁定”在结构中,可用于缓冲吸能,避免二次冲击[22,23,29]。(3)结构从一个稳态转换到另一个稳态时,会将存储的应变能突然释放,达到快速变形和放大输出力的目的,这一特性有望应用于高效、快速驱动[28,30]。(4)在变形后,结构无需外界能量持续输入即可保持变形形状,可设计为节能夹持器、存储器等,不需要电源即可保持任何一种状态[31,32]。(5)多稳态结构具有丰富的变形能力[33,34]。随着增材制造技术(即3D打印)的发展,目前已经可以制备新型的较为复杂的多稳态结构[35]。常规力学超构材料在卸载后结构变形无法维持,从而限制了其实际应用,而多稳态力学超构材料可以克服这些限制,在移除外部载荷时可以维持转换后的稳态结构[25]。因此,多稳态力学超构材料显著拓宽了超构材料的应用领域,如图1所示的能量吸收[23,27,29,36,37]、软驱动器/软体机器人[38-41]、机械存储/逻辑运算[16,31,42-44]、波调控[45,46]等等。
1 双稳态单元设计原则
1.1 双稳态和单稳态
通过调节几何参数,大部分双稳态单元会表现出3种不同的非线性力学响应,即双稳态、单稳态和简单稳态。双稳态是多稳态结构中最基本的结构形式,在变形过程中,当施加在结构上的载荷F超过特定的阈值Fcr时,双稳态的第一稳态会迅速转变成第二稳态,即表现为突弹跳变效应。同时,结构在卸载之后不需要持续的能量输入就可以保持突变之后的状态。而当施加反向作用力,第二稳态又会转变成第一稳态。双稳态在每个稳态构型下结构都具有一定的承载能力,即该稳态构型是锁定的[28,47]。结构在稳态转换过程中会呈现出如图2(a)蓝色实线所示的非线性力-位移曲线。可以看到双稳态结构在突弹跳变过程中出现了负值力,也就是说在形变过程中结构由开始的正刚度变为负刚度,稳态转换完成之后再次变为正刚度[48,49]。单稳态是指结构在变形过程中只有一个稳定的构型[28,50]。当施加的载荷超过阈值时,结构会发生变形(存在突弹跳变现象),但是在载荷卸载之后,结构无法保持变形的形状(即恢复到原来唯一的稳定状态),需要施加外力才能保持变形形状。在变形过程中,单稳态结构也会呈现与双稳态结构类似的非线性行为,存在负刚度现象,但是其力-位移曲线一直都在x轴的上方,即无负值力,如图2(a)绿色虚线所示。与双稳态结构和单稳态结构不同,大多数稳定的结构(简单稳态)受到施加的载荷时发生非线性的弹性变形,且没有突弹跳变失稳[28]。载荷卸载之后,稳定结构恢复到初始的稳态状态,其力-位移曲线无负刚度现象。
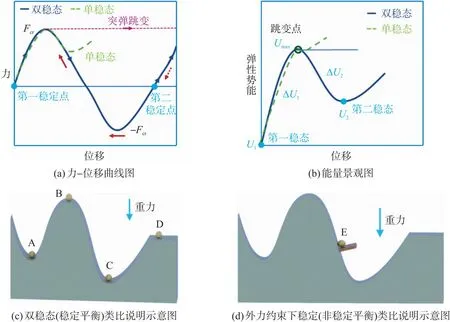
图2 双稳态和单稳态的力-位移曲线图、能量景观图及稳定与非稳定平衡类比说明示意图
1.2 能量势垒
双稳态结构在稳态转换过程中的能量曲线如图2(b)中所示,可以看到,在这一转换过程中结构将经历1个能量极大值(不稳定点)和2个极小值(稳定点)。对于双稳态而言,两个稳定构型是整个结构的能量低点状态(两个极小值U1、U2),对应力-位移曲线上正刚度段与x轴的交点。在这2个稳定平衡态中间,结构还要经历一个处于能量高点(极大值Umax)的不稳定平衡状态[21],即力-位移曲线负刚度段与x轴交点。因此在稳态跃迁过程中,结构先吸收能量再释放能量。单稳态结构对应图2(b)中绿色虚线部分,它只有1个能量最小值,因此是单稳态的[26,28,47]。施加的载荷使得结构发生变形,外界输入的能量以弹性势能存储在结构中,当载荷卸载时,由于无法保持变形形状,存储的弹性势能会被释放。
从一种稳态到另一种稳态转换时的能垒ΔU为能量的极大值与极小值之间的差值,即ΔU1=Umax-U1表示从稳定状态1跳变到稳定状态2或ΔU2=Umax-U2表示从稳定状态2跳变到状态1,如图2(b)所示。在双稳态结构上施加的载荷要克服能垒才能发生突弹跳变。ΔU1和ΔU2也分别对应力-位移曲线中x轴上方和下方所围成封闭区域的面积。因此,可以通过控制位移来测量ΔU,从而获得驱动双稳态状态转换所需的功率和能量[28]。在双稳态结构发生突弹跳变过程中,通过跳变点之后的能垒对应于结构的能量释放,以加速运动和放大动力的形式输出。双稳态结构的能垒取决于其结构形式、几何尺寸和材料特性。通过调整结构参数,可以进一步增强双稳态结构的动力输出和跳变阈值力。
可以将能量图与“山丘上的小球”类比[51-53],如图2(c)所示。A点和C点表示稳定(态)点,即在这些点上的小球是稳定的,对应能量景观图中的极小值。在微小扰动下(如很小的推力),偏离的小球还是会回到原来A和C位置,因此,微小的扰动并不能改变小球在A和C点的平衡状态,这种平衡属于稳定平衡状态。B点是不稳定(态)点,此处势能高,对应能量景观图中的极大值点。小球受到微小扰动会向势能低点A或C运动,此时系统向能量最低状态运动的趋势不可能返回势能高点B,因此,微小的扰动会改变小球在B点的平衡状态,这种平衡状态属于不稳定平衡状态。处于D点的小球受到的微小扰动无论朝向哪个方向都不会改变其自身的能量,D点为无数个平衡态,即随遇平衡状态,是不确定的状态,因为任何扰动仅仅会使小球滚到其受扰动的位置上。而E点也可以看成是一个稳定点,不过是在外力约束下稳定,如图2(d)。
1.3 双稳态单元及其多稳态力学超构材料
1.3.1 梁、桁架和柔顺机构
杆件是力学构件中最常见和基本的研究对象,其中梁、桁架单元和柔顺机构是双稳态结构中最简单的单元,包括4种常见的形式,如图3所示。
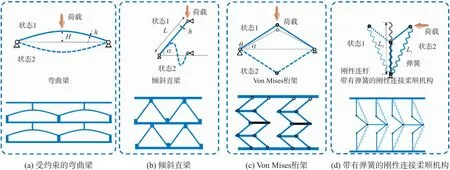
图3 双稳态梁、桁架单元和柔顺机构
(1)受约束的弯曲梁[25,54],在水平力下预屈曲双固支曲梁,如图3(a)所示。通过调控几何结构参数,受约束的弯曲梁结构可以实现单稳态和双稳态。比值为Q=H/h的受约束的弯曲梁,Q值的增加会导致梁力学响应发生变化,如式(1)所示[54-57]。当Q值较小时(Q≤1.23),梁没有突弹跳变失稳,即简单稳态;当Q值高于临界值(Qmon=1.23),梁展示出单稳态的突弹跳变失稳;当Q值进一步增加到高于Qcr=2.31的阈值时,梁变为双稳态。弯曲梁Q值计算公式如下
(1)
式中:H为梁的高度,h为梁的厚度。
(2)倾斜直梁[23,58],一端固定,另一端可以垂直移动的倾斜直梁,如图3(b)所示。在恒定的梁长细比h/L下,当倾斜角α从0°增加到接近90°时,梁从简单稳态、单稳态到双稳定性连续转变[23]。在恒定的α下,减小h/L使梁变为双稳态。几何相图显示,一般来说,要设计双稳态约束倾斜梁,要求h/L和α的值都在一定范围内,如式(2)所示。对于h/L≤0.1的细长弹性梁,它表现出很大的α可调范围,从30°到70°。而对于0.1 倾斜直梁的双稳态满足条件为 (2) 式中:h为梁的厚度,L为梁的长度,α为直梁的倾斜角。 (4)带有弹簧的刚性连接柔顺机构,如图3(d)所示。柔顺机构也叫柔性机构,是由刚性和柔性构件组成的结构,可以通过弹性变形来实现运动[60]。带有弹簧的刚性连接柔顺机构由2个可旋转的刚性连杆与1个自由旋转的关节相连接,以及1个用于储能和释放能量的预张弹性线性弹簧[61]。与具有柔性铰链的连杆机构不同,基于弹簧的连杆机构的双稳态是由刚性约束和预拉伸弹簧引起的,这要求2个刚性连杆的长度L2>弹簧的初始长度L1,如式(3)所示。 带有弹簧的刚性连接柔顺机构单稳态和双稳态判断依据为 (3) 式中:L2为弹簧连杆长度,L1为弹簧初始长度。 1.3.2 薄壳结构 壳结构也是力学中常见的构件,双稳态薄壳结构包括曲面(单弯曲面和双弯曲面)、三浦折纸、水弹折纸、球形圆顶(穹顶)壳结构、克雷斯林(Kresling)折纸结构和“<”形吸管薄壳结构等,如图4所示。 图4 双稳态薄壳单元 弯曲面中的双稳态由无量纲几何参数η控制[65-67]。当η较小时,如η<<1,表现出弱的弯曲-拉伸耦合,有利于单稳态模态的平滑变形,而没有双稳态。当η超过ηc的临界值时,如η>>1,由于与非零高斯曲率相关的几何非线性,具有强弯曲-拉伸耦合的双稳态模式优先。弯曲面的双稳态判断依据为 (4) 式中:w为宽度,h为厚度,κ0为曲面的曲率。 三浦折纸[68-70]和水弹折纸[71]是2种常见的双稳态折叠结构。在受到轴向载荷时,它们可以迅速发生稳态转换,上下弹出,如图4(b)所示。这2种折纸结构的变形模式类似于Von Mises桁架结构,如图3(c)所示,折纸的面可以当做刚性面,折痕当做柔顺的铰链。 单胞内部存储的应变能U可表示为 U=[km(γm-γm0)2+kv(γv-γv0)2]/2 (5) 式中:km和kv为谷折痕的扭转刚度,k=EI/l(E为材料的杨氏模量,I为截面惯性矩,l是弯曲支点的长度)[72]。γm和γv分别是通过相关运动学建模确定的折叠峰角和折叠谷角。γm0和γv0分别是峰折痕和谷折痕的初始角度。 由于γm和γv由折叠模式中的几何参数(例如水弹折纸中的扇形角α)决定,km和kv与柔性折叠的弯曲刚度有关,因此三浦折纸和水弹折纸结构中的双稳态行为可以很容易地通过几何参数进行调节,例如扇形角α、其余折叠角γm0和γv0,以及折叠中使用的长度和宽度或材料。 (6) 式中:ν为泊松比,h为厚度,R为半径,Ф为开口角。 Kresling折纸结构(也叫对角折纸、三角圆柱折纸)是由薄壁圆柱受轴向压缩和扭转时屈曲形成的图案[43,76],如图4(d)所示。其特点是沿着扭转方向呈一定角度交替的折叠峰和折叠谷,顶部和底部是2个正多边形。Kresling折纸结构的运动模式是扭转屈曲变形和轴向收缩运动(即拉压-扭转耦合)。Kresling折纸不是刚性可折叠的,并且不能通过纯粹的折痕折叠而变形。Kresling折纸中的双稳态与材料特性无关,仅取决于其几何参数[47]。由于运动学不相容性,其扭曲压缩需要三角形面弯曲或/和拉伸以适应折痕角的高度非线性变化,因此,难以获得双稳态临界条件的解析解,这可以很容易地通过数值方法获得。 “<”形吸管薄壳结构也是一种常见的双稳态薄壳结构,它由2个圆锥壳通过折痕连接[29,34],如图4(e)所示。在拉伸或压缩载荷作用下,单元会在“展开”和“折叠”2个状态间转换。其变形模式与Von Mises桁架和带有弹簧的刚性连接柔顺机构类似。“<”形吸管薄壳结构的双稳态和单稳态取决于θ1和θ2,当其中一个角度(如θ1)固定时,随着另一个角度(如θ2)的增加,结构会从单稳态向多稳态转变。 1.3.3 其他双稳态结构 此外,还有一些其他的双稳态单元,如卡扣结构、旋转铰链可展剪纸结构、方块-扭曲折纸结构、双孔模板结构等,如图5所示。 图5 其他双稳态单元 卡扣结构是一种在工程中常见的连接部件,日常生活中随处可见,如瓶盖、笔帽、尼龙扎带、设备外壳等。卡扣结构通常由2个部分组成,如图5(a)所示:凸出的卡扣部分和凹陷的卡槽部分[22]。在受到轴向压缩时,卡扣进入卡槽,卡扣发生变形,当超过临界载荷时,卡扣会迅速装配完成(即突弹跳变现象)。卡扣结构的双稳态特性与插入面角度α和开口比d/D有关,当插入面角度0°<α<90°,开口比0 对于旋转铰链可展剪纸结构[77,78],如图5(b)所示,在拉伸载荷作用下,结构的铰点处会承受很大的变形。当载荷增加到一定阈值时,结构会跳变到第二个稳定构型。组合旋转铰链可展剪纸单元可以得到多稳态剪纸结构。研究发现,弯曲铰链的厚度对结构的稳定性起到关键作用,尤其是铰链厚度比t/l和旋转单元的宽度比a/l。结构变形稳定状态下局部最小应变能Emin与其应变能势垒Emax的比值,即:η=Emin/Emax。当η<1时,结构具有双稳性。从带圆形图案的方形和三角形设计结构的双稳态相图可知,η=1时,结构是单稳态。稳定变形状态下的主应变分布表明,应变主要集中在铰链处,其余部分的变形可以忽略不计。 当受到轴向拉伸/压缩时,方块-扭曲折纸结构和旋转铰链可展剪纸结构都会发生扭转变形,并展示出双稳态特性。方块-扭曲折纸结构中[79],如图5(c)所示,中间实线为山折痕,虚线为谷折痕。方块-扭曲折纸结构的变形过程存在拉紧、解锁和展平3个阶段。通过允许小面弯曲变形,方形扭曲可以折叠,并且当弯曲与折痕能量比足够大(即大于1 000)时,它提供了双稳态。 双稳态双孔模板结构是一种准2D结构,由2种孔径尺寸不同的圆孔组成[80-82],如图5(d)所示。在几何尺寸满足一定的条件时,结构是双稳态的[83,84]。在压缩时,圆孔向内收缩,即由伸展状态转变为弯曲状态。当0.10≤εx≤0.16时,双孔模板结构显示出突弹跳变单稳态特性;当εx不断增加,即εx≥0.17时,双孔模板结构展示出双稳态特性[82]。 将上述的双稳态单元串联、并联或串并联组合,可以形成具有多个稳定构型的多稳态结构,即多稳态力学超构材料,其形式可以是1D链结构、2D网状结构和3D空间结构。例如,受约束的多层预屈曲梁(图3(a))、多层倾斜梁(图3(b))、多层Von Mises桁架(图3(c)),基于弹簧的多稳态连杆机构在将双稳态单元串联起来形成链状连杆机构的同时增加额外的连杆和弹簧构成并联机构,以形成多层带有弹簧的刚性连接柔顺机构(图3(d))。在单轴压缩载荷下,各层结构会发生突弹跳变,显示出双稳态性能,多层结构具有多个稳定构型。 近年来,双稳态结构因其独特的力学性能受到广泛关注,对比稳定、单稳态结构而言,双稳态结构具有以下优异特性。 (1)可重复使用特性:当外界施加的载荷超过一定的阈值,双稳态结构会发生状态转换。载荷撤去之后,结构可以保持变形状态。若再施加相反的载荷超过一定阈值后,结构又可以恢复为初始的稳态。因此,双稳态结构具有可重复使用特性,在实现可重复使用器件、机械能吸收等方面提供了一种新的设计方法[27,29,85]。 (2)能量存储与吸收特性:与传统耗能方法(塑性变形、断裂等)不同,由于双稳态结构在稳态转换之后可以保持变形形状,一部分应变能被“锁定”在结构中,因此可以捕获能量。当位移载荷移除时,结构不会回弹,这与弹簧结构相反。因此,双稳态结构可用于缓冲吸能,避免回弹引起的二次冲击[23,25,27]。 (3)快速变形和放大输出力:当双稳态结构从一个稳态转换到另一个稳态时,通过不稳定性可以实现快速变形和放大输出力。在突弹跳变过程中,由于存储的应变能突然释放,在几十毫秒内发生快速变形,可以在低驱动能量下产生较大的输出力。这种快速变形和放大输出力的性能为高性能驱动装置提供了有效途径,有望解决驱动过程中缓慢响应问题[26]。 (4)低能耗:常规结构在外部刺激(机械力、电场、磁场等)下可以发生变形,但是需要持续的外部能量(如电能或持续做功)输入才能保持所需形状。而双稳态结构在完成稳态转换后可以保持变形形状,因此,不需要消耗额外的能量[34]。利用这一特性可以将双稳态结构设计成夹持器,以实现节能驱动,在没有能量输入情况下握持物体。此外,还可以用于二进制信息存储,不需要额外电源保持任何一种状态[28]。 (5)丰富的变形能力:将多个双稳态单元串联和/或并联,可以形成不同稳定构型的多稳态结构,在外部驱动下,多稳态结构可以展示出多种形态变化并具有可重构性,为多级能量吸收和波调控提供了一种可行的方案。此外,也可应用于在狭窄空间中的可重构软体机器人以及可弯曲和扭转的可重构机械臂[28,86]。 多稳态力学超构材料通常可以用增材制造(即3D打印)的方法来制备。Bertoldi等[23]通过直接墨水书写(Direct ink writing,DIW)技术,将粘弹性聚二甲基硅氧烷(Polydimethylsiloxane,PDMS)油墨从喷嘴中挤出,构建基于倾斜直梁的3D多稳态力学超构材料(图6(a))。马力等[87]采用热塑性弹性体材料(Thermoplastic elastomer,TPE)基于熔融沉积建模(Fused deposition modeling,FDM)技术制备了double-U型的多稳态力学超构材料(图6(b))。卢明辉等[88]提出通过立体光固化(Stereolithography,SLA)技术制备具有多稳态、可重新编程和可重复使用特性的卡扣力学超构材料,如图6(c)所示。Myant等[89]采用PolyJet技术制备了多平面力学超构材料,以实现布尔“与/或”机械逻辑(图6(d))。Akbarzadeh等[27]通过基于选择性激光烧结(Selective laser sintering,SLS)技术来打印Schwarz’s Primitive壳多稳态结构(图6(e)),与其他打印方法(如FDM、SLA和DIW)相比,SLS的一个突出优势是未烧结的底层粉末为下一层提供支撑,这适用于这种具有悬垂的多孔壳超材料。近年来,微纳3D打印也广泛用于制备介观和微观多稳态力学超构材料。Song等[32]使用了投影显微立体光刻(Projection micro stereolithography,PμSL)技术打印了介观尺度的NAND逻辑门,如图6(f)所示。Kadic等[37]提出了多稳态微晶格(图6(g)),采用双光子光聚合(Two-photon photopolymerization,TPP)技术在微米尺度上实现了用于吸能的多稳态力学超构材料。此外,还有一些传统的制备方法,如切割(机械切割、激光切割)、模具法等,由于这些传统的制备方法较为常规,本节对这些方法不做介绍。相信随着材料制造技术(如增材制造、微纳加工、激光切割等)的不断发展,更多复杂结构的多稳态力学超构材料将被制备出来。 图6 多稳态力学超构材料制备方法 由以上分析可知,多稳态力学超构材料具有可重复使用、能量吸收、快速变形和放大输出力、节约能源和丰富的变形能力等特性,在众多领域都有广泛的应用。在这一节中,本综述将从应用角度,如能量吸收、软驱动器/软体机器人、机械存储/逻辑运算、波调控等,综述多稳态力学超构材料的研究进展。 能量吸收在日常生活、工业生产中都有着很重要的应用,传统的吸能结构/材料对冲击能量的吸收和耗散往往是通过破坏性的塑性变形或者断裂来实现的[90,91]。这种方式存在一个很大的弊端,由于其吸收能量的过程是破坏性的,所以结构/材料在单次使用后被破坏无法继续使用,即这种结构/材料是不可重复的,会导致资源的浪费和环境污染[92]。此外,这类结构/材料往往对复杂环境适应性差,缺少灵活的部署能力[93-95]。面对这些不足,研究人员采用多稳态力学超构材料来解决以上面临的挑战[36,58,96]。 双稳态结构从低能量状态转换为高能量状态时,从外部系统吸收能量,这个过程是可重复的。将双稳态结构组装成多稳态力学超构材料,在受到冲击载荷时,其双稳态单元切换到高能状态,冲击能量以弹性势能形式存储在结构中[23,27,29,85,88]。因此,多稳态力学超构材料常用于收集或耗散机械能[23,25,27,29](图7)。 图7 多稳态力学超构材料在能量吸收方面的应用 美国哈佛大学Bertoldi研究团队较早提出用多稳态力学超构材料来吸收冲击能量[23],如图7(a)所示。该团队利用1D斜臂梁结构设计了可以重复吸能的多稳态力学超构材料。当斜臂梁的倾斜角和长度满足特定的关系时,这种结构显示出双稳态特性。这种结构可以拓展到2D结构甚至3D结构。通过试验演示了该超构材料在高空物体坠落时的冲击防护作用。在受到外界的冲击载荷时,一部分机械能会被存储在弯曲的斜臂梁中,发生碰撞事故时可以起到对人员和设备的防护作用。这种结构制作简单,成本较低。然而这种结构一旦被制作完成,其力学性能就不再可调,缺少可编程性。此外这种结构强度较低,能量吸收有限。同年美国普渡大学Zavattieri团队采用了类似的结构(图7(b)),提出一种相变多孔材料[54],这种相变多孔材料其实就是多稳态力学超构材料,展示出类似于相变材料的性质,即在不同的温度下材料的物质状态不同。在微纳尺度上,多稳态力学超构材料也可以展示出优异的机械能吸收能力。德国卡尔斯鲁厄理工学院Kadic团队提出了多稳态微晶格(图7(c)),他们采用双稳态弯曲梁在微米尺度上实现了用于吸收机械能的超构材料[37]。同样,为了实现对机械能量的吸收,加拿大麦吉尔大学Pasini团队采用双弧形结构,设计出了一种多稳态力学超构材料(图7(d))。在外力的作用下,双弧形结构可以在“打开”和“闭合”这2种稳态之间进行转换,将机械能以弹性变形的形式存储在结构中,从而吸收外界的冲击能。另外,在施加相反的作用力时,这个结构可以将储存的机械能释放出来。然而,这种基于双弧形结构设计的超构材料强度比较低,因此在工程应用中缺乏稳定性[25]。 在Bertoldi团队的研究基础上,清华大学周济团队设计了一种结合斜臂梁和卡扣结构的多稳态力学超构材料(图7(e)),可用于能量吸收[22]。这些人工结构可以将卡扣顺序插入配合的凹槽中。该结构的机械性能可以通过调整结构的几何参数来调整。但是,由于卡扣中间没有开孔,在受到外部载荷时,卡扣被迫变形,增加了磨损,容易损坏。此外,清华大学赵治华和美国加州大学金丽华团队合作开发了一种编程颗粒超构材料[52],用于可重复能量吸收(图7(f))。这种可编程颗粒超构材料的制备工艺非常简单,只要将固体颗粒用可拉伸部件(如弹性扎带、弹性膜)捆绑在一起即可,固体颗粒之间的摩擦增加了单元的稳态数。在外部载荷下,单元会发生稳态转变,可拉伸部分发生弹性变形,固体颗粒则会相对彼此滑动。外界的能量一部分被储存为弹性应变能,另一部分变成摩擦热能耗散,从而实现了能量吸收的目的。控制变形发生的位置和顺序,可以实现不同的能量吸收的能力,并通过试验验证了该超构材料的能量吸收特性。 北京航空航天大学陈玉丽团队受到刺猬的启发,提出了一种全新的机械像素阵列设计策略,即利用吸管(3D薄壳结构)制作了一种具有超强力学性能可编程性、复杂形状可重构性且可高效重复吸能的多稳态力学超构材料[29],如图7(g)所示。这样把超构材料的单元离散化,增加了设计自由度。演示试验表明这种多稳态力学超构材料可以吸收冲击能量,以保护易碎物品。但是,由于这种超构材料无边界约束,在受到冲击时容易飞溅。此外,吸管是薄壁壳结构,加工困难,难以拓展到微纳尺度。加拿大麦吉尔大学Akbarzadeh团队设计了可编程多稳态穿孔壳体,利用2种穿孔策略在Schwarz’s Primitive壳体上实现了多稳态[27](图7(h))。通过设计壳体的几何参数和选定的穿孔轮廓,使得具有椭圆孔的壳体实现了双稳态、交错穿孔的壳体实现了多稳态。并通过数值模拟、弹簧理论建模和力学试验验证了穿孔壳体超构材料的多稳定性。通过玩具车低速冲击试验以演示材料的能量吸收能力,测量撞击后的回弹距离,具有自接触设计的穿孔壳体反弹距离最小,吸收了大部分的冲击能量。然而,由于薄壳结构制备困难,强度低易损坏,在工程应用中缺乏稳定性。 在受到外界冲击载荷时,双稳态结构单元会从一个稳态转换到另一个稳态,转换过程中,这种转换是可逆的,外界输入的能量会以应变能形式储存在结构中。因此,多稳态力学超构材料展示出优异的能量吸收性能,如可逆性和可重复性,且在变形时以弹性变形为主,克服了传统吸能结构不可重复使用的缺点。此外,多稳态力学超构材料还具有可编程性,可以实现快速灵活部署,提高了在复杂环境下的使用能力。然而,多稳态力学超构材料也存在一些缺点,如常规的多稳态结构强度较低、能量吸收弱且不能自动恢复。为此,可以通过优化结构设计、使用能量密度高的材料、与传统吸能结构结合,并引入多级吸能结构,以提高能量吸收能力。在多稳态结构中加入可恢复机制,添加响应外部刺激材料,可以设计多稳态力学超构材料以提供更多不同类型的不寻常物理特性,例如设计带有形状记忆材料的双稳态结构,通过改变设计参数来调整触发温度,当加热到触发温度时,热双稳态结构会恢复形状[97]。 由于机器人具有感知、决策和执行能力,因此,自机器人技术开发以来,便不断地渗透到各个领域[98,99]。机器人可以辅助甚至替代人类完成危险、繁重、复杂的工作,提高工作效率与质量[100,101]。然而,目前大部分机器人都是用刚性材料(如金属)制成的,它们具有良好的精准性、高效的执行效率,但是由于其弹性变形的能力较弱,对于较为复杂的外部障碍,无法表现出柔性材料固有的自适应性[40,102,103]。此外,刚性机器人对人体的亲和性差,容易对人体造成伤害。而软体机器人可以与人类安全地交互合作,具有连续性、柔顺性和适应性,表现出一定的安全性和弹性变形能力,能够适应较为恶劣的封闭环境,抗压并且能够缓解应力集中现象。同时软体机器人优异的柔顺性和适应性,可以在受限空间内实现自我导航[100,104]。 近来,利用双稳态和多稳态设计各种高性能软体机器人引起了人们对软体机器人的兴趣[28,30]。与稳定的驱动结构相比,具有双稳态和多稳态结构的软体机器人可以利用多稳态结构突弹跳变时的快速转变以实现快速响应。此外,普通稳定驱动器需要外部持续供能才能保持变形形状,而多稳态结构可以在无需持续能量输入情况下保持变形形状。当多个双稳态单元串联、并联或混合时,可以形成多稳态结构,极大地丰富了结构的变形能力。 美国北卡罗来纳州立大学尹杰团队模仿猎豹奔跑状态(脊背弯曲和伸展),构建了软体机器人[61](图8(a))。该机器人的骨骼脊柱是由带有弹簧的刚性连接柔顺机构构成,具有双稳态性,软气动弯曲致动器作为骨骼肌。充气和放气时,软驱动器可以使得柔顺结构的2个稳定状态实现快速转换,从而实现“奔跑”运动。对比常规的软体机器人(最快速度仅有每秒0.8个体长),由于双稳态结构的突弹跳变快速转换,该软体机器人的速度是常规软体机器人的3倍。美国加州理工学院Daraio和瑞士苏黎世联邦理工学院Shea团队设计了一种“自驱动”机器鱼[105],如图8(b)所示。使用形状记忆聚合物来充当机器鱼的“肌肉”,为变形提供动力,在低温时卷曲、高温时伸展。“肌肉”与具有双稳态性能的Von Mises桁架结构连接,形状记忆效应驱动双稳态结构发生稳态转变。由此控制双稳态结构上的鱼鳍进行转动,便可以使得机器鱼在水中游动起来。将多个稳态组合起来可以实现更复杂的运动,如连续运动、转弯、后退。然而,由于形状记忆聚合物驱动力较弱,实现强大的驱动和连续复杂运动依然具有挑战。美国北卡罗来纳州立大学Ghosh开发了一种基于双稳态曲面的软介质驱动器[62](图8(c))。这种制动器是将2个正交预应变介电薄膜粘合到支撑层的两侧,在电驱动下绕横向和纵向弯曲的2种稳定状态。在演示试验中,将制动器放置在“青蛙”的口中,以模仿捕捉动作。 图8 多稳态力学超构材料在软驱动器和软体机器人方面的应用 Kresling折纸结构由于其双稳态性,以及具有扭转屈曲变形、轴向收缩运动(拉压-扭转耦合)特性,也常用于制作软体机器人。美国伊利诺伊大学Tawfick团队较早提出多稳态软体机器人,该团队采用直流电机驱动双稳态Kresling折纸爬行机器人[106],如图8(d)所示。2个Kresling折纸多胞平行排列,可以完成旋转动作。利用各向异性摩擦原理,该爬行机器人实现了行走运动。此外,为了防止主体旋转,将双稳态单元以反手性连接可以实现直线运动。美国斯坦福大学赵芮可团队利用类似的原理,设计了仿蠕虫Kresling软体爬行机器人,并将其小型化,实现了毫米级软体爬行机器人,如图8(e)所示,这种软体爬行机器人可以应用于地表勘探、管道检测、肠胃内窥镜检查等工作空间受限的场合[40]。在磁场的远程控制下,可以实现爬行动作,控制磁场方向实现机器人沿任意路径导航,如“Z”、“O”路径。另外,赵芮可团队将Kresling折纸单元串联成多胞结构,然后制成机械臂[30],如图8(f)所示。这种机械臂是受到章鱼触手灵活变形以实现行走、游泳、捕食等动作的启发。在外加磁场的控制下,Kresling单元可以实现伸缩和万向弯曲变形,即当施加面内的转矩时实现伸缩变形,施加面外转矩时实现弯曲变形。将多个Kresling单元组装成多单元仿生机械臂,通过磁化设计和精准的磁场控制,机械臂实现了万向弯曲、伸缩和扭曲动作,可以抓取和操作物体。这种磁驱动仿生机械具有可远程无线控制、响应快速和易于小型化的优势。他们团队还利用Kresling折纸实现了一种可以同时实现水路两栖多模态运动、可控液体药物释放、固体药物运送的毫米机器人[107]。 瑞士苏黎世联邦理工学院Studart和美国普渡大学Arrieta报道了一系列由柔性板组成的力学超构材料,这些柔性板由可重构双稳态3D圆顶阵列组成[31],如图8(g)所示。这种超构材料的3D圆顶结构可以在局部尺度上发生可逆的翻转,即双稳态性,由此可以生成可编程的多稳态形状,并且在全局尺度上具有可调的力学响应。通过3D打印制备的机器人抓手具备蓄能皮肤、可存储信息和计算空间中分布的力学信号的功能。演示试验中,构造了一个简单的机器人抓手。当圆顶凹陷时,抓手臂保持打开状态。当施加少量气压以使圆顶变得凸起时,抓手臂就会闭合得足够紧,以抓握住一块小重量的物体。由于使用了双稳态结构,当翻转圆顶使抓手闭合时,结构可以将能量存储起来,因此,在没有外界能量输入情况下依然可以保持抓握。同样,美国马萨诸塞大学Crosby利用3D圆顶结构制作可以跳跃的聚合物凝胶[41],如图8(h)所示。条状的聚合物凝胶用溶剂溶胀,再置于聚四氟乙烯薄片上消胀,溶剂蒸发后,条状的凝胶会变为弯曲形状。利用这种性能,将聚合物凝胶制备成3D圆顶结构,可实现最大位移变化,且无需外部电源。演示试验展示了3D圆顶聚合物凝胶软体机器人的弹跳动作,该软体机器人可以完成爬楼梯的动作。 软体机器人的连续性、柔顺性和适应性提供了传统刚性机器人无法实现的新功能。将双稳态结构引入到软驱动器和软体机器人中,具有以下诸多优势:(1)响应快,双稳态结构可以在低驱动能量和小输入力下进行突弹跳变,以实现快速移动和放大输出力,以及毫秒级别快速变形,从而克服软物质作用力小、响应慢的缺点。(2)节能,双稳态结构不需要提供额外能量可以保持变形构型。而传统的软驱动器保持变形需要连续的驱动输入。(3)丰富变形构型,将多个双稳态单元串联、并联或混合,可以形成不同构型多稳态结构,以适应狭窄空间的可重构机器人、多模态机器人,以及可弯曲和扭转的可重构机械臂。然而双稳态软驱动器/软体机器人也存在一些限制和挑战:(1)很难做到精确控制,在双稳态结构突弹跳变的边缘和跳变过程中精确控制较难,这可以通过准确控制突弹跳变之前和之后的关键突弹跳变点来精确化[61,108]。(2)单驱动输入以实现丰富的形状变化具有挑战性。随着双稳态单元数增加,结构的复杂性会急剧增加,这会导致控制系统变得复杂。这可以通过调控双稳态单元的能垒来调整单次驱动下的形状变形或施加外部约束控制互连单元的变形[35]。(3)使输出具有鲁棒性较为困难,需要较高的储能能力,产生足够的力输出,克服较大的能量势垒。软驱动材料柔软性的内在限制,削弱了集成双稳态机器人的性能。可以采用具有更高工作密度和功率密度的软智能材料(如扭转人造肌肉[109])。 目前人类使用的硬件系统一直沿用冯·诺依曼结构,这种结构采用了二进制作为数字计算机的数制基础,如指令的发送和接收、数据的存储和读写都是二进制的[110]。尽管以电子晶体管和磁存储器为基础设计的硬件系统在计算速度以及存储密度方面都具有优势,但是机械逻辑系统具有强的鲁棒性,有利于在极端条件(如高温和强辐射)下应用[111]。由于双稳态结构可以提供2个不同的稳定构型,因此可以用机械状态表征0、1逻辑信息(字节),并设计出功能完备的逻辑运算(如AND、OR、NOT和NAND、NOR等)[42]。将双稳态单元组装成多稳态力学超构材料,可以提供丰富的可控稳定状态,在信息处理和逻辑运算中有重要的应用[16,43,112]。 2016年美国哈佛大学Bertoldi团队利用柔性介质中储存的弹性势能得到稳定传播的机械信号并实现了机械逻辑门操作[44],如图9(a)所示。该柔性介质采用了双稳态Von Mises桁架结构,并设计成链状结构,在具有不同耦合刚度的链状结构中能够实现机械二极管,通过调节系统的能量势垒可以实现机械逻辑操作(如“与”、“非”门)。力学超构材料的逻辑功能通常由其布局决定,一旦设计完成,在使用过程中很难改变。现有的力学超构材料逻辑系统大多功能不全或不能实现时序逻辑。因此,不具备较强的机械计算能力。由此,清华大学陈常青团队提出了一种可重编程的力学超构材料,包括基本逻辑的周期阵列和功能完整的机械逻辑门[42](图9(b))。在一系列电磁的连续激励下,这种超构材料可以实现重新编程。由双稳态弯曲梁阵列的开关状态分布确定加载位置,以执行不同的逻辑功能(如“与”、“或”、“非”等逻辑门)。试验演示了可重编程的力学超构材料在通用组合逻辑和时序逻辑(信息存储)方面的应用。 图9 多稳态力学超构材料在机械存储和逻辑运算方面的应用 此外,该系统的信息存储能力被证明有利于机械逻辑电路的集成化设计。美国劳伦斯利弗莫尔国家实验室Pascall和美国加州大学洛杉矶分校Hopkins团队提出了一种基于增材制造的微机械逻辑门的新型数字式机械计算方法[32](图9(c))。该团队利用3D打印技术制造了机械逻辑门,并能够执行任何一种逻辑运算。这种机械逻辑门利用可屈曲多稳态桁架结构实现布尔运算,以机械力为输入,位移为输出,无需电子组件。该机械逻辑门不受尺寸限制,可以缩小到几微米。这些3D打印的逻辑门可嵌入任何类型的架构材料中,与周围环境发生相互机械作用。由于该系统在内部处理和存储数字数据时不需要电力,非常适用于高辐射、高温、高压等电子设备很难发挥作用的场合。北京理工大学方岱宁和清华大学张一慧团队提出了一种用于三元逻辑运算和振幅调制的可扩展三稳态分层力学超构材料[113],如图9(d)所示。其基本单元是X形曲梁结构,在连接杆左/右移动下提供2个附加稳态,即具有三稳态。按照自下而上的方案对单元进行扩展所构建的分层力学超构材料能够实现稳态数量的指数增加。利用这种独特的三稳态结构设计了基本的机械三元逻辑门,以机械力作为输入,位移为输出,试验演示了基本的逻辑运算(如“或”、“与”、“非”门等)。这种独特的三稳态结构设计还展示了以前无法实现的复杂逻辑运算符。与二元逻辑门相比,三元/多值逻辑门可处理更多信息,可有效降低设计复杂度并加快串行算术运算速度。三元逻辑门在模糊逻辑电路、异步电路等中也具有独特的应用。英国伦敦帝国理工学院Myant团队提出了一种多平面力学超构材料,可以实现布尔与/或机械逻辑运算[89],如图9(e)所示。通过驱动各向异性3D单胞控制双稳态Von Mises桁架的屈曲响应以执行布尔逻辑,通过改变单胞之间的间距可以表现为与/或门特性。美国俄亥俄州立大学赵芮可团队(现美国斯坦福大学)和佐治亚理工学院Paulino团队将磁响应材料和双稳态Kresling折纸结构结合构成一种新型的多功能驱动器[114](图9(f))。在单一的外加磁场控制下,可以实现多个驱动单元的独立控制,并应用于信息存储。演示试验中,实现了模数转换和信息存储功能。该团队设计了一种三位存储器,在分布式控制驱动下实现了存储信息的改变,并用LED实时显示存储的信息。这种多功能驱动器可以被动地感应外界负载的大小,通过磁驱动主动地做出响应,集成驱动、传感和计算功能于一体,符合机器人的感应-决策-响应设计思路。 虽然最初的力学超构材料展示出了新奇的力学性能,但是它们一旦被编程之后便无法再改变,因此没有表现出类似数字设备(如硬盘驱动器)的可重编程性。瑞士洛桑联邦理工学院Pauly和Reis团队通过使用一种可平铺的力学超构材料设计框架克服了这一挑战。该材料在单胞级具有稳定记忆特性[16],如图9(g)所示。这种设计包括一组物理二进制元素(m位),类似于数字位,并清楚地描述了写入和读取阶段。每个m位都可以使用磁驱动在双稳态3D圆顶壳的平衡之间移动,从而在2个稳定状态(充当内存)之间独立且可逆地切换。在结构发生变形后,每一种状态下都具有显著不同的弹性力学响应,并且能够可逆循环,直到系统重新编程。将一组二进制指令编码到平铺阵列上会产生明显不同的力学性能,可以使刚度和强度在一个数量级上变化。基于软材料的柔性器件/设备正在被广泛应用,然而其控制系统依旧是刚性的硬阀和电子控制。美国哈佛大学Whitesides团队通过设计一种气动软双稳态阀来实现数字逻辑门操作[115](图9(h))。双稳态阀是由3D圆顶结构,通过控制其突弹跳变调整信号输入源,依靠3D圆顶膜的突弹跳变不稳定性来扭结内管,并以二进制高/低输入和输出压力运行。该结构实现了NOT、AND和OR数字逻辑门,可以用于制造置位/复位锁存器、双向移位寄存器、边缘检测器、数模转换器和拨动开关。这种气动软双稳态阀具有良好的可扩展性,在稳定状态下不消耗能量,并可以通过单一设计实现多功能性,为开发自主控制、不涉及电子接口和硬质组件的软设备提供了有效的策略。瑞士苏黎世联邦理工学院Studart和普渡大学Arrieta报道的由柔性板组成的力学超构材料不仅在软驱动器和软体机器人中具有良好的应用前景,在机械存储方面也展示出了一定的潜力[31]。在3D圆顶双稳态结构中可以存储局部弹性势能,并生成多个稳定的可重构几何形状。3D圆顶结构类似于计算机数据的“1”和“0”。通过按一定顺序在某些位置按下圆顶,然后根据柔性薄板的形状机械地“读取”数据。对这样的柔性薄板进行“编程”,就可以在没有电源或中央处理器的情况下实现机械计算。 相较电子形式的计算和信息处理而言,目前双稳态结构实现的机械存储和逻辑运算速度慢,小型化和集成化方面还不尽人意。然而,双稳态结构与周围环境相互作用,通过二进制状态(0、1)存储比特信息,不需要额外的电源,能源效率高。因此,机械存储和逻辑运算非常适用于高辐射、高温、高压等电子设备很难发挥作用的场合。此外,微纳制造技术(如微纳3D打印、光刻等)的发展促进了微纳器件的发展,有利于机械逻辑门的小型化。随着软驱动器和软体机器人的发展,双稳态结构的可逆二进制用作软机械逻辑门(AND、OR、NOT)设计的机械逻辑计算、机械存储器在软驱动器和软体机器人的自主控制中具有很好的潜在应用。融合信息处理、材料科学和机器人学的思想,增强了与环境交互、适应环境的能力[42,112,116]。 多稳态系统通常通过从一个稳态到另一个稳态的连续内部跃迁过程,以顺序方式释放能量来响应外部刺激[117,118](图10)。也就是说,双稳态结构在初始高能状态,输入信号推动第一稳态回到低能量状态,释放的能量推动下一个稳态单元到低能量状态,循环到最后,稳定非线性传输波以高的保真度和可控性在多稳态系统中传播。这一系统是内部互相关联的,类似于“多米诺效应”,一个很小的初始能量就可以产生一系列连锁反应[119,120]。 图10 多稳态力学超构材料在波调控方面的应用 美国加州理工学院Kochmann和Daraio团队设计了一组由双稳态单元组成的多稳态系统,其中心有一对磁铁,能够传播单向过渡波[121](图10(a))。阵列中的双稳态单元承受来自其相邻单元的磁铁的斥力,因此,当其中一个双稳态单元切换状态时,它会触发阵列中其余双稳态单元的顺序切换,产生1D过渡波。穿过该系统的过渡波速度是恒定的,可以通过改变磁体的强度或柔性双稳态单元之间的距离来调节。此外,该团队还提出了使用另一种双稳态结构对波传播进行调控。他们研究了由弹簧-质量块连接(类似于Von Mises桁架)的周期性双稳态单元链的非线性动力学行为,其约束排列会引起大变形突弹跳变的不稳定性[122](图10(b))。由此产生的负刚度效应在周期性介质中产生了3种不同的波传播方式,具体形式取决于振幅,即小振幅下是线弹性波,中等到大振幅下出现弱和强的非线性波。基于该结构所设计的新型力学超构材料在线性和非线性状态下具有可控波传播能力,超出了之前主要基于线性弹性波传播的概念。 美国哈佛大学Bertoldi团队也采用了双稳态Von Mises桁架结构,制备的柔性介质可以稳定传播机械信号[44](图9(a))。使用柔性材料制备可以产生大变形的双稳态屈曲梁,在行波波前的刺激下释放能量,从而使大振幅信号在没有外界激励下达到无损耗传播的效果。结构对能量的吸收和释放平衡导致波稳定的传播,并且由于材料内在的耗散性阻隔了其他信号,使得波的传播具有高保真、可预测和可控制的特点。通过调整等效弹簧的弹性常数,可以控制过渡波在系统中的传播速度,并对2.3节所述的3D打印机械二极管的驱动阈值进行编程。Bertoldi团队还研究了密封流体腔内双稳态3D圆顶壳阵列的过渡波传播[45],如图10(c)所示。由于2个双稳态圆顶壳之间的流体腔将保持恒定的体积,双稳态圆顶壳的突弹跳变过程将传播到其相邻的壳。传播过程中的能量耗散会影响传播距离,为了延长传播距离,该团队通过改变壳的厚度来调节能量势垒,以允许过渡波在有限距离上双向传播。过渡波通过双稳态壳的传播可以通过顺序扩展软体来模拟蛇的直线运动,从而在软体机器人运动中找到潜在的应用。另外,Bertoldi团队与瑞士苏黎世联邦理工学院Kochmann团队合作提出了2D多稳态力学超构材料,此类超构材料能够通过调整过渡波在其架构中的传播来实现可预测和可编程的运动[46](图10(d))。这些2D超构材料由单独的单稳态单胞组成,当排列成周期性晶格时,它们显示出了双稳态。最初处于拉伸(打开)状态,在一端扰动长阵列的单胞,以诱导超构材料局部转变为压缩(闭合)状态,从而触发转变波以恒定的方式通过材料传播速度。通过在这些力学超构材料的结构中引入缺陷,可以对过渡波传播进行编程以产生蛇形运动和功能形状变形。缺陷相对于力学超构材料边界的密度和位置可以控制过渡波的传播速度和方向。 美国宾夕法尼亚大学Raney团队用试验、数值和解析的方法研究了由三稳态元素链组成的力学超构材料中的过渡波(图10(e))。过渡波可以在高度可调的三稳态能量范围内从不同的稳定相启动。这些波通过耦合的平动和旋转运动传播,如果不相容类型的过渡波碰撞,就会形成静止畴壁。由于畴的形成和传播是完全可逆的,这种独特的非线性行为可以在新类别的可重构超构材料中加以利用。 由于多稳态系统可以产生互相关联的状态转换,在外界激励下以一定顺序释放能量。双稳态结构在2个状态之间切换可以用于过渡波在系统中传播。这种过渡波的速度和方向可以通过利用多稳态系统中的机械不稳定性来编程,从而增加力学超构材料的设计范围[123-125]。利用跨多稳态系统的过渡波控制,还可以实现可编程软体机器人运动、可调能量吸收和机械逻辑器件(如开关或滤波器)的设计。 多稳态结构展示出丰富的力学性能,除了应用于上述领域外,在可重构结构/器件、减震器、可展开结构/器件以及材料本构模拟器等诸多领域都有应用。 传统的超构材料一旦制备而成,结构便固定下来,无法进行重构。由于多稳态结构的形状变形能力以及复杂空间构型,可应用于可重构器件中(如可重构天线、可重构谐振器等)。可重构天线阵列中各单元之间根据实际情况灵活可变,通过调整可变器件,实现天线性能的可重构。天津大学陈焱团队通过设计一组具有特定运动范围的新型弹性铰链,并基于剪纸结构设计了一种新型三稳态单元及一系列可编程的多稳态超结构(图11(a)),并将该三稳态单元应用于频率可重构天线的设计中以实现5G三频段通讯[126]。此外,北京理工大学方岱宁、宋维力、陈浩森团队利用经典的方块-扭曲折纸结构展示了一种多材料3D打印的三稳态折纸结构[127],如图11(b)所示。通过调控聚合物异质结构的材料特性和几何参数,可以改变折纸结构折叠势能。该团队推导了在方块-扭曲折纸构型中获得多稳态结构的设计原理。在热激励条件下,可变形结构面内刚度快速大幅度降低,导致结构面内弯曲自由度增加,从而通过释放折痕处弹性势能来实现自展开。利用这种独特的特征和设计原理,该团队设计并制作了具有5种不同工作频率的可重构折纸天线,实现了可编程多输入/输出通信系统,可以大幅提高信道容量和通信可靠性,在大规模多输入/输出系统的5G关键技术中具有潜在应用。另外,浙江大学陈红胜和美国东北大学刘咏民团队设计了基于多稳态三浦折纸的振器[69],如图11(c)所示。三浦折纸单元沿着第3个方向变形,诱导了开口环谐振器的净电偶极子和磁偶极子相互平行或反向平行,从而导致强烈的手性响应。因此,可以通过切换该超构材料的稳态以控制电磁性能。 图11 多稳态力学超构材料在其他方面的应用 多稳态结构中的局部不稳定性在预定的作用力下发生,结构转换时,采用较低能量进入新的稳态构型,可以防止超过临界力的传递并消耗能量,基于这个原理可以将双稳态结构应用于隔振方面。哈尔滨工业大学王兵团队提出了一种实时可调的气动负刚度(分为单稳态和多稳态)力学超构材料[128],如图11(d)所示。这种超构材料的基本单元是3D圆顶壳结构,通过气动驱动可以实现多级模式转换,具有隔振性能。随着内部压强的增大,超构材料的共振频率降低,这主要是由超材料中的流固耦合引起的。随着内部压强的逐渐减小,共振频率增加。其原因在于随着超构材料的收缩,立方支撑结构相互连接,超构材料趋于刚体。以色列理工学院Givli团队受蛋白质结构的启发,精心设计多稳态力学超构材料以用作纳米级减震器[129],如图11(e)所示。利用结构不稳定性反复过滤掉超过允许水平的力(如来自振动环境的力),对“目标”进行机械保护。这利用了局部结构不稳定性的力敏感构建块,不稳定性被设计在预定的力水平下发生。在结构切换后,材料以较低能量进入新的亚稳态结构。因此,防止了超过临界水平的力传递并消耗了能量。 汕头大学杨楠团队受到显示器对像素编码的启发,设计了由许多单元构成的棋盘结构[130](图11(f)),每个单元都具有多稳态特性,可以独立改变状态。棋盘结构单元具有不同的模式及其声学特性,并在其中选取一些有趣的特性以及相应的编码方式,如:滤波特性、波导特性、透镜特性和隐形特性。也就是说通过利用多稳态的形状变形并结合不同的声学特性来构造可编程声子晶体,并通过试验和模拟进行了验证。 以色列理工学院Peretz团队将气体、液体和多稳态弹性胶囊结合起来,用于制造一种具有多种稳定状态的人造流体,如图11(g)所示。多稳态胶囊是多个连接的双稳态单元,由2个相反方向的不同圆锥截头体组合而成。通过一个截头体的倒置在展开和折叠状态之间切换实现双稳态性,这个过程会产生显著的体积变化。胶囊的弹性多重稳定性赋予流体多重稳定的热力学特性,包括在标准大气条件下捕获和储存能量的能力。 清华大学张一慧和黄永刚、美国西北大学Rogers团队提出的3D结构的机械引导组装方法因为在生物集成电子和光电器件中的广泛应用而受到越来越多的关注[131]。该方法将2D薄膜图案通过压缩力的作用变形成目标3D结构,并通过改变压缩变形的路径以实现3D结构在不同构型之间的可逆切换(即具有多稳态性),如图11(h)所示。此外还设计了二十多组不同结构构型,通过试验和有限元方法对可行性进行了验证。这一技术不但能应用于多种特征尺度的结构设计,还能与现代化微电子制备工艺相兼容,适用于导体、半导体、绝缘体等各种材料类型甚至集成电路系统的构建。 可展开系统可以将大型结构压缩到很小的体积,常见的包括由相互连接的杆单元组成的机构,这些杆单元可以同步展开和收缩,有时通过双稳态单元锁定结构。美国哈佛大学Hoberman和Bertoldi团队设计了可展开的、多稳态的可展开刚性壁结构。通过几何分析和试验,构建了一个可通过单一流体压力输入的可展开双稳态折纸图形库[132]。然后将这些单元结合,进一步实现了宏观尺度(米级别)功能结构的建筑,如拱门和应急避难所等,如图11(i)所示。这些系统在展开后会锁定在适当的位置,并通过其坚硬的表面提供坚固的外壳。 传统材料由于受到结构拓扑和复杂耦合作用,其力学性能是无法定制的。基于双稳态结构,北京航空航天大学陈玉丽、潘飞团队提出了一种新颖的“构建楼梯”策略,用于定制和重新定制力学超构材料的目标力学行为[33](图11(j))。类似于用砖块建造楼梯,定制或重新定制材料的目标应力-应变(力-位移)曲线,通过可视化地堆叠双稳态单元来实现多水平梯度加载曲线。 由于多稳态结构丰富的力学性能,多稳态结构显著拓宽了力学超构材料的应用领域。利用多稳态结构的丰富且可重复变形能力,在制备可重构器件(如可重构天线、可重构谐振器)上展示出优势。多稳态结构在状态切换时可以防止临界力的传递并消耗能量,因此在隔振方面也发挥着作用。通过将不同的声学特性编程到双稳态结构上,可以展示出丰富的声学性能。将多稳态结构设计成可展开系统,在折叠与展开时起到锁定的作用,用于设计宏观尺度的功能性建筑。此外,双稳态结构可以用于构建目标的应力-应变曲线。 本文综述了近十年来多稳态力学超构材料的研究进展。首先介绍了双稳态单元的特点及其设计原则。从能量角度分析了双稳态结构在状态转换过程中的稳定点与不稳定点,以及结构对能量的存储与释放。总结了双稳态结构的基本类型,包括:(1)梁、桁架、柔顺机构;(2)曲面和薄壳结构;(3)其他结构,如剪纸、卡扣结构等。详细讨论了多稳态力学超构材料的应用前景,包括能量吸收、软驱动器/软体机器人、机械逻辑门/存储、波调控等。 尽管多稳态力学超构材料的研究取得了重大进展,但在设计和应用过程中仍然存在许多挑战: 多稳态力学超构材料通常强度较低、无法自行恢复,限制了其可重复使用范围,同时其能量吸收能力较传统吸能材料较弱,在面对较高能量时应用受限。为此,可以通过优化结构设计、使用能量密度高的材料、与传统吸能结构结合、引入多级吸能结构等方法来解决强度较低、能量吸收弱的缺点。此外,可以在多稳态结构中引入外部刺激响应性材料,从而实现主动变形能力。 多稳态结构的快速变形为软驱动器/机器人提供了快速驱动方式。然而,多稳态结构在稳态转换时的突弹跳变不稳定性,给软驱动器/机器人的精确控制带来挑战。通过控制突弹跳变前后的跳变点可以提高对多稳态结构变形的控制精度。此外,多稳态结构的变形往往是单驱动下进行的,这使得结构控制变得复杂。这可以通过调控双稳态单元的能垒来调整单次驱动下的形状变形或施加外部约束控制互连单元的变形来解决。 虽然与电子形式的计算和信息处理相比,基于多稳态力学超构材料的机械存储和逻辑运算速度上非常缓慢,小型化和集成化程度也较低。然而,双稳态结构能够在不供电的情况下,通过二进制状态存储比特信息,这一特性使其可以适应高辐射、高温、高压等特殊服役环境。此外,将机械计算与软驱动器/机器人相结合,可以实现自主控制,增强了与环境交互和适应环境的能力。随着微纳制造技术(如微纳3D打印技术)的发展,机械计算的小型化和集成化也有望得到解决。 多稳态结构展示出丰富的力学性能,使其在其他领域也都有相应的应用。由于多稳态系统是互相关联的,一个很小的初始能量即可产生一系列连锁反应,以顺序方式释放能量来响应外部刺激。因此,双稳态结构在2个状态之间切换可以用于过渡波在系统中的传播控制。通过利用多稳态系统中的机械不稳定性来控制这种过渡波的速度和方向。因此,可以实现可编程软体机器人运动、可调能量吸收和机械逻辑器件(如开关或滤波器)的设计。此外,利用多稳态结构具有丰富且可重复变形的能力,可以制备可重构器件(如可重构天线、可重构谐振器)。多稳态结构也可以应用于隔振领域,主要因为其在状态切换时可以防止临界力的传递并消耗能量。将其他结构具有的特殊性能(如声学特性)编码到双稳态结构上,通过稳态转换可以展示出丰富的声学性能。多稳态结构的变形和锁定能力,结合可展开系统,可用于设计宏观尺度的功能性建筑。此外,双稳态结构也可以用于构建目标的应力-应变曲线。
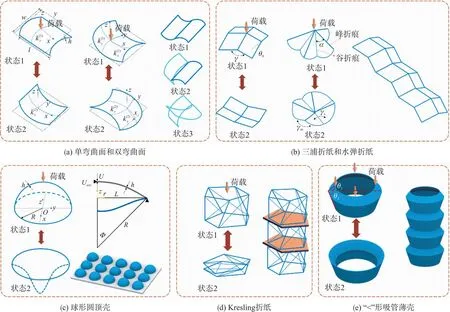


1.4 双稳态结构特性
1.5 多稳态超构材料的制备

2 多稳态力学超构材料的应用
2.1 能量吸收

2.2 软驱动器和软体机器人

2.3 机械存储和逻辑运算

2.4 波调控
2.5 其他应用
3 结论与展望
