不同粗骨料粒径混凝土动态压缩强度的离散性研究
2024-03-04丁俊升王江波高光发杜忠华董雪花
丁俊升,王江波,高光发,杜忠华,董雪花
(南京理工大学 1.理学院;2.机械工程学院,江苏 南京 210094)
混凝土作为一种重要的防护材料,被广泛应用于高层建筑、隧道、桥梁、大坝等民用和军用建筑。混凝土是由水泥、水、骨料、矿物掺合料和外加剂按一定比例搅拌、凝结硬化而成的一种复合材料,有较理想的抗冲击和承载力。作为一种复合材料,其力学性能比其他均质材料更为复杂,其中各组分占比与尺寸都影响着材料的动静态力学性能,最终表现出脆性破坏。因此,研究混凝土材料异质性引起的动静态力学响应问题显得尤为关键[1-3]。
混凝土材料中粗骨料通常占比很大,并且尺寸大出细骨料很多,所以不同的粗骨料粒径很大程度影响着其动静态力学性能的发挥。近年的研究中发现,粗骨料的体积分数和粒径大小直接影响混凝土材料的动静态力学性能。Hao等[4]对砂浆和骨料粒径为4 mm、8 mm的混凝土材料,以及19%、42%的不同粗骨料体积分数的混凝土材料进行对比研究,试验结果表明:粗骨料在混凝土材料中的贡献相当大,特别是在相对较高的应变率下。混凝土材料的动态强度总是高于不含粗骨料的砂浆样品,并且随着粗骨料尺寸增长,混凝土材料异质性也随之上升,最终导致动态增长因子(Dynamic increase factor,DIF)减小,试验结果更加分散。增加混凝土中粗骨料的体积分数会使混凝土材料在高应变率下具有更高的动态抗压强度。方秦等[5]基于粗骨料大小、形状及空间随机分布建立三维混凝土细观模型,得出结论:在相同粗骨料粒径条件下,骨料体积率越高,混凝土动态强度也越高;相同粗骨料体积含量条件下,粗骨料尺寸越大,混凝土动态强度越低。Kim等[6]对最大粗骨料粒径为13 mm、19 mm、25 mm的混凝土和砂浆试件进行动态压缩试验,分析认为:为避免粗骨料尺寸引起混凝土材料的异质性效应,至少保证混凝土材料截面直径为粗骨料最大粒径的3倍。王江波等[7]在不同强度砂浆及对应强度下不同粗骨料粒径混凝土材料的准静态压缩与劈裂试验中得出:粗骨料粒径的增大,对混凝土的抗压强度、抗拉强度、杨氏模量的影响均呈现为先增大后减小的趋势。Wu等[8]用ABAQUS建立二维中尺度模型,对骨料面积分数进行分析,结果表明:粗骨料含量较高会对混凝土的动态抗拉强度有不利影响,并且随着粗骨料面积分数增加,界面过渡区(Interfacial transition zone,ITZ)面积也会随之增加,混凝土抗冲击性降低。
综上所述,大多研究者只是针对粗骨料粒径与体积分数的影响进行了研究,少有考虑在材料测试这个尺度上粗骨料粒径对混凝土异质性的影响,基于此,本文分别进行准静态压缩试验和分离式霍普金森压杆(Split Hopkinson pressure bar,SHPB)动态压缩试验,定义粒径系数(粗骨料最大粒径与试件直径之比),并根据数理统计知识,针对混凝土动态力学性能试验中由于粗骨料粒径产生的异质性问题进行计算分析,给出参考粒径系数,作为试件加工的一个参考指标,提高后期试验数据的可靠度。这一离散性算法对其他复合材料试验中离散性问题分析具有参考价值。
1 力学性能试验
1.1 试验材料选取与制备
试验选用中强度砂浆和混凝土,试验材料由硅酸盐水泥、细骨料(河砂)、粗骨料、水、矿粉和减水剂等组成。试验材料为不同粗骨料粒径的混凝土与砂浆,砂浆选用除粗骨料之外的所有材料组成制备,混凝土根据粗骨料粒径不同制备出3种,各组分材料占比保持一致。
试验采用张家港海螺水泥有限公司生产的普通硅酸盐水泥;细骨料选用河砂,为保证混凝土(砂浆)强度,采用方孔筛进行细度模数试验,得到砂的细度模数为2.39;粗骨料选用灰色花岗岩,粗骨料在筛选时选择4 mm和8 mm、10 mm和14 mm、22 mm和26 mm的筛网,两两一组对粗骨料进行筛选,最终得到3种不同粗骨料粒径材料,尺寸为4~8 mm、10~14 mm和22~26 mm;矿粉选用中国青岛产S95级矿渣粉;减水剂选用聚羧酸高性能减水剂。
砂浆与混凝土试样的配比在表1中给出,3种混凝土试样除粗骨料粒径不同外,其他组分保持一致,粗骨料含量占比约为37%。样品制备参考Guo等[9]的制备流程:把各材料按表1比例搅拌混合、定型、养护28天、切割打磨试件。最终得到试件直径为68 mm,准静态和动态压缩试件长径比分别为2和0.5,即φ68×136±0.1 mm和φ68×34±0.1 mm。部分试样如图1所示。混凝土试样的命名由直径和骨料粒径两部分组成,例:D68-G8表示选用直径为68 mm和最大粒径为8 mm的粗骨料加工而成的混凝土材料。

图1 部分混凝土试样

表1 混凝土试样配合比
1.2 动静态压缩试验
采用816 Rock System MTS试验机对砂浆和3种混凝土试样分别进行准静态压缩试验,应变率设为10-4/s。将试件连接试验机,置于压头与底座之间。如图2所示,缓慢加载,采集整理试验数据,每种试样测得3组有效数据。
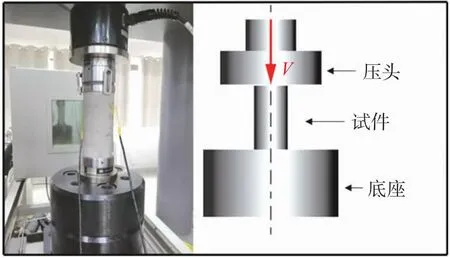
图2 准静态压缩试验
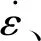
(1)
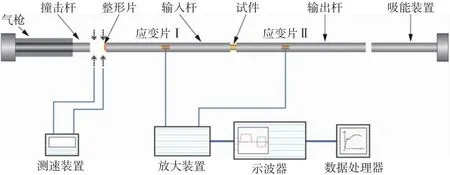
图3 霍普金森压杆测试系统示意图

图4 SHPB动态压缩试验

表2 SHPB装置的主要参数
式中:Ab是杆的横截面积;As和Ls分别为试件的横截面积和长度;Cb和Eb为杆的弹性波速和杨氏模量;εr(t)和εt(t)为反射波和透射波。
2 结果分析与讨论
2.1 应力-应变曲线
对准静态单轴压缩试验数据进行整理,得出4种试样的有效静态抗压强度数据各3组,并对每组数据分别求平均值,得到平均静态抗压强度如表3所示。

表3 试样平均静态抗压强度
根据测试系统绘制应力-应变曲线,如图5所示。每种试样测得3组有效数据,为了更清楚地展示应力-应变曲线图,选取每组试验中应力峰值在中间的曲线,作为有效曲线绘制成图。
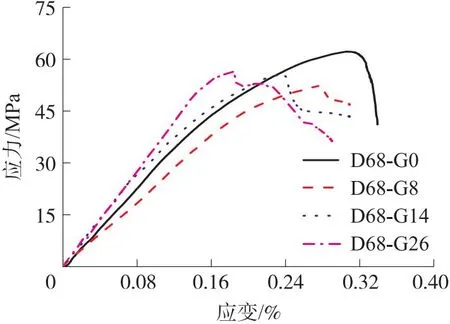
图5 准静态压缩应力-应变曲线
试验分析得出:(1)不同粗骨料粒径的混凝土材料具有类似的应力应变曲线特征;(2)加入粗骨料后,混凝土材料的极限压缩强度与极限应变均低于砂浆材料;(3)随着粗骨料粒径的增大,混凝土材料的单轴压缩强度随之提高。这说明粗骨料的加入引起了材料整体强度削弱,因为混凝土材料在水化过程中,会形成一种胶凝材料,粘附于粗骨料表面形成一层ITZ,过渡区属于混凝土强度薄弱区,一般强度只有水泥浆体的50%左右,其厚度在5~100 μm。在此认为混凝土在单轴压缩过程中,ITZ强度较低,是混凝土破坏的起始,裂纹的扩展也是从ITZ开始沿砂浆基体扩展直至破坏。
对动态压缩试验数据进行采集,并绘制4种试样的典型应力-应变曲线,如图6所示。

图6 4种试样的典型应力-应变曲线
由图6可知4种试样具有明显的应变率效应。试样在加载初期呈线性上升趋势,并且前期动静态试验的应力-应变曲线基本重合,认为试样的杨氏模量不受应变率效应影响。随着应力的不断增加,应力-应变曲线呈非线性增长,证明试样受压开始出现局部裂纹,裂纹的扩展影响到结构的整体性能,随后试样很快达到峰值应力,材料结构失效,应力-应变曲线迅速下降,直至失去承载能力。从图中可以看出:静态下应力-应变曲线的峰值应变在0.2%~0.3%之间;动态下应力-应变曲线的峰值高低受应变率影响,随着应变率的不断增加,应力-应变曲线的峰值应力不断提升,材料的峰值应变在0.3%~0.7%之间。
2.2 DIF
DIF由欧洲混凝土协会(CEB)[10]规定并开始使用,定义为单轴动态抗压强度σd与准静态抗压强度σs之比。随后广大研究者达成共识,将其作为评估混凝土材料应变率效应、材料抗冲击性能的重要指标。近30年众多研究者纷纷对应变率与DIF的关系进行研究,并总结了相关规律。本文借鉴众学者经验,进行对比,最终参考了CEB 1990、Bischoff、Chen和Liu等[10-13]论文中的对数曲线拟合经验,自定义拟合公式如下:过渡应变率选择30/s,经验公式前面选用指数型,后面选用对数型
(2)
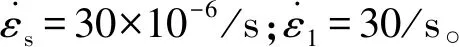

图7 68系列应变率与DIF关系图
从图7中发现,应变率在30/s~120/s区间时,DIF随应变率的增加而增加。用经验公式对数据进行拟合发现,D68-G0、D68-G8、D68-G14拟合曲线在同一应变率下的DIF差值在20%左右,D68-G26数据相比更为分散,应变率80/s~100/s区间内,DIF最高可达1.8左右,最低仅1.3左右,误差在35%左右,这是由于粗骨料粒径不同引起的材料异质性问题,最终导致试验阶段DIF的波动性较大,并且波动性有随应变率升高而扩大的趋势。为解决动态压缩强度下数据离散性较大的问题,引入数理统计知识,对离散性问题进行定量分析,研究粗骨料粒径与动态性能测定中离散性问题的内在联系。
2.3 数据离散性分析
2.3.1 变异系数与粒径系数
为分析离散性问题,引入了变异系数CV,定义为标准差与平均数的比值,在概率统计学中主要用于计算数据的离散程度,可以消除单位和(或)平均数不同对2个或多个资料变异程度比较的影响。本文考虑到影响因素有应变率与DIF 2者,最终采用多元CV计算方法,公式由Albert和Zhang共同提出[14]
(3)
式中:μ为应变率的对数与DIF值组成的平均向量;Σ为应变率的对数与DIF组成的协方差矩阵;T为转置符号。为了更好地反映粗骨料变化所带来的动态强度离散性问题,定义无量纲粒径系数λ为粗骨料最大粒径d与试件直径D的比值(λ=d/D)。
2.3.2 数据处理流程
下面以D68-G0试样为例,作以下处理,其他试样采用同样的方法进行拟合,如图8所示。
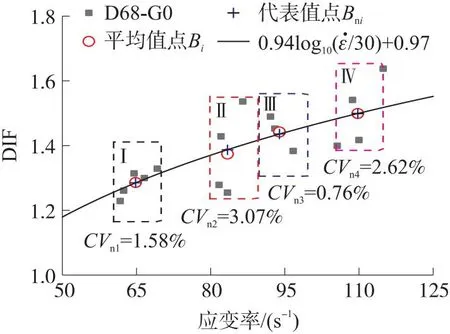
图8 拟合流程图
(1)以应变率为参考量,对相近的应变率区间进行分段处理,并求出每区间段的平均值点Bi(应变率,DIF)图中用红圈表示出,图中数据按应变率大小分为60~70、80~90、90~100、105~115这4段。
(2)将Bi点应变率代入拟合式(2)得到拟合曲线,然后把平均值点Bi的应变率代入拟合公式求得修正后的代表值点Bni图中用蓝色十字标出。
(3)对代表点Bni中的应变率取对数,DIF不变,整理作为平均向量μ,每分段内的数据与平均向量的差值组成协方差矩阵Σ,将其代入式(3)求变异系数CVni。
(4)对4个CVni求平均值,CV=(CVn1+CVn2+CVn3+CVn4)/4=2.01%,用于反映G0粒径系数下的离散度情况。
(5)根据每组试验中粗骨料的差异,做粒径系数λ与CV的关系图,进行分析。
2.4 λ与CV关系
运用上文提到的数据处理方法,计算得出D68-G0、D68-G8、D68-G14、D68-G26这4种试样的平均值点Bi和应变率与DIF曲线关系, 如图9所示,并且给出了经验公式系数A2、A3与不同粒径系数下CV见表4和表5。分析得出:(1)砂浆属于均质材料,没有粗骨料的掺入,所以对比混凝土材料在动态压缩试验中具有更小的离散性,CV最小;(2)随着粗骨料粒径的增大,混凝土材料异质性增加,导致动态压缩试验数据离散性增加。

图9 各试件应变率与DIF曲线

表4 经验公式系数A2、A3

表5 不同粒径系数下的CV
为了进一步分析离散性问题,参考了Kim等在文献[6]中的试验数据,以此加大试验数据量,用来分析在多种粒径系数下材料的CV,试验数据如图10所示。

图10 50系列、75系列应变率与DIF曲线(试验数据参考文献[6])
应用上文提到的方法,最终得到经验公式系数A2、A3与不同粒径系数下CV汇总于表4、表5。同时,绘制λ与CV关系图,如图11所示。选取砂浆CV最大值2.48%,作为离散性参考线,对高于参考线的点作线性拟合交参考线交于点(0.34,2.48)。可以看出混凝土材料粒径系数λ在0~0.34区间内异质性变化不明显,在0.34达到转折点,之后快速上升,试验数据表现出明显的离散,证明材料的异质性已经显著影响其动态力学性能。当粒径系数λ<0.34时,认为纯砂浆CV是其本身的属性决定的,而粗骨料的加入使材料特性发生改变,使试验数据出现波动,但整体都低于2.48%,所以认为粗骨料的加入并没有明显影响其材料的异质性;当粒径系数λ>0.34时,材料的异质性明显增强,砂浆和粗骨料的材料属性差异被放大,骨料与砂浆之间的ITZ属于强度薄弱区,裂缝会优先选择沿ITZ区域开展,导致材料力学性能下降,并且随着骨料粒径的增大,ITZ面积也会有所增大,最终强度的不均匀导致骨料的吸能效果被大大削弱,严重影响混凝土的动态响应[8,15,16]。

图11 异质性影响线曲线
结果表明:λ<0.34时,粒径系数对混凝土动态压缩强度离散性影响较弱,λ>0.34时,随粒径系数的增长,离散性明显增加,最终认为λ=0.34为混凝土材料异质性阈值。
针对本试验分析得出:(1)不同最大粗骨料粒径混凝土的应变率与DIF曲线均高于砂浆材料,认为粗骨料对混凝土材料的动态抗压强度有重要影响;(2)DIF随应变率的增加而增加;(3)当λ<0.34时,同等应变率下,粒径系数越大,DIF越大,材料动态压缩性能越好;(4)本试验中D68-G26试样的λ>0.34,认为试验离散性过大,已经影响到动态压缩性能测定,没有参考价值。
3 结论
利用φ80 mm口径的SHPB装置对最大粗骨料粒径分别为8 mm、14 mm、26 mm的混凝土与砂浆4种试件进行动静态压缩试验,对粗骨料粒径不同引起混凝土材料异质性与DIF变化的问题进行分析,主要得到以下结论:
(1)在准静态压缩试验中发现,砂浆的抗压强度高于不同粗骨料粒径混凝土的抗压强度,且随着粗骨料最大粒径的增加,混凝土的抗压强度也逐渐增大;在动态压缩试验中发现,在试件加载初期应力-应变曲线呈线性上升趋势,随着应力不断增加,曲线转变为非线性上升,当达到峰值应力后,曲线迅速下降;峰值应力与应变率大小有关,随应变率提高,峰值应力不断提高。
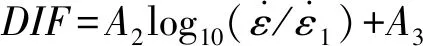
(3)定义无量纲粒径系数λ,通过计算得到异质性影响曲线,结果表明:当λ<0.34时,混凝土材料异质性变化不明显;当λ>0.34时,粗骨料粒径过大已经影响到了混凝土的动态响应,材料异质性明显增强。
(4)本文通过试验与数理统计方法,总结了混凝土动静态力学性能和制定了一套计算试验数据离散性的方法,并分析了粗骨料粒径变化所带来的试验离散性变化规律。离散性研究对今后工程与试验中粗骨料粒径的选取有指导意义。对于粗骨料百分比含量影响试验离散性问题、粒径系数λ对抗侵彻能力的影响问题以及其他复合材料异质性问题分析具有参考价值。
