基于FFT 的波动方程VOFFLC 控制

汪 洋, 江厚顺, 汪 杰 许冬进 尹 彪

(1.长江大学石油工程学院，武汉 430100; 2.扬州工业职业技术学院化学工程学院，扬州 225127)

0 引言

很多受控体系核心参数的变化规律，无法使用常微分方程(ODE)表述，必须使用偏微分方程(PDE)才能准确描述[1]。PDE 的无穷维特性使其几乎不能以封闭形式求解(除了一些特例)，而采用差分或有限维ODE 来近似PDE 是处理PDE 求解问题的有效方法[2]。例如，文献[3]利用本征正交分解(Proper Orthogonal Decomposition, POD)将PDE 降维成ODE，然后求解未知参数；文献[4–5]利用有限差分(FDM)将PDE 转为代数系统，文献[6]采用有限元法(Finite Element Method, FEM)将PDE 转为ODE，然后辨识未知参数。

在工程技术上，常常要求对某些物理量加以控制，使其变化规律满足技术上的要求[1]。方程模拟方面，由Cooley 和Tukey[7]提出并发展出来的快速傅里叶(FFT)技术的可用性强，在软件中有较好的植入性，可以实现周期性边界条件下的波动方程数值模拟。控制系统方面，文献[8–9]提出采用模糊控制(Fuzzy Logic Controller, FLC)和分数阶PID 控制(Fractional Order Proportional Integral Differential, FOPID)相关理论的变阶次分数阶模糊PID 控制VOFFLC；作为一个自适应系统，VOFFLC 可以实现在运行中不断测试误差e和误差导数ec，并根据模糊控制规则在线调整所有五个控制器参数，以增强系统。

本文采用FFT 算法将案例的波动方程从时域PDE 转化到频域ODE，利用VOFFLC控制器搭建简洁的自适应控制体系，以实现对波动方程的时域控制。这样，可以实现类似边界控制的结果；同时，在空间维度上可以实现向量级控制，即实现对该维度上任意函数形状、插值函数或者散点的向量级控制，而这是边界控制做不到的；同时，为实现复杂工程技术向量级核心参数的自适应控制研究提供有用的思路。

1 数值理论

1.1 FDM 理论

考虑一维波动方程问题

其中a为正常数，f(x,t)、φ(x)、ψ(x)和β(x)为已知函数。首先，以空间步长h=1/N、时间步长τ=T/M分别将x轴上区间[0,1]、t轴上区间[0,T]分成N、M等分，得xi=ih(0≤i ≤N)和tk=kτ(0≤k ≤M)。同时引入步长比s=ατ/h，并采用简写uki=u(xi,tk)，得差分格式

1.2 FDM 理论

对于在任一有限区间上满足Dirichlet 条件的函数u(x)(x ∈(−∞,∞))，傅里叶变换和其逆变换为[10]

后面采用简写ˆu(k)=F[u(x)]和u(x)=F−1[ˆu(k)]。此外，u(n)(x)表示为u(x)的n阶导数，则函数的求导运算在傅里叶变换的作用下，可以转化为相对简单的代数运算

基于上述法则，利用傅里叶变换将偏微分方程中空域或时域上的求导运算简化为频域上的代数运算，求解后再通过傅里叶逆变换得到空域或时域上的结果。

1.3 VOFFLC 控制

1.3.1 FOPID 控制

将波动方程的PDE 模型经过FFT 变换成ODE 模型后，尝试采用集中参数的理论，引入自整定强鲁棒控制器，以实现波动方程空间维度上向量参数的优化控制。这里优化控制是从一类允许的控制方案中找出一个最优的控制方案，使系统的运动在由某个原始状态转移到指定的目标状态的同时，其性能指标值为最优[11]。

首先，具有以下理想传输功能的PID：

进而，由Podlubny[12]提出FOPID 控制，格式为PIλDµ，传递函数为

其中λ和µ分别为积分阶次和微分阶次。

在实际分数阶PID 控制器中，因为积分环节是由滤波器逼近的，λ ＜1 时并不能完全消除稳态误差，所以最好用下面的形式重建积分器[13]

1.3.2 VOFFLC 控制器规则

本文采用VOFFLC 控制器来完成控制任务[8–9,14]。本文采用文献[8]的VOFFLC 模糊规则，允许FOPID 控制器的所有五个参数随着系统结构作为VOFFLC 输出的变换而变化。

通过实验总结的PID 参数增量(ΔKp,ΔKi,ΔKd)和阶次λ、µ参数增量(ΔKλ,ΔKµ)的调节方法如表1 和表2 所示[13]。其中模糊规则被分为7 个模糊集：负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)和正大(PB)。

表1 λ 和µ参数增量的模糊推理表

2 数值分析应用

本文采用文献[15]中的一维波动方程的模型：一根两端固定、没有受到外力的弦，若只研究其中的一段，在不太长的时间里，固定端来不及对这段弦产生影响，可以认为固定端是不存在的，弦的长度为无限大，且假定数值计算区间足够大，在一定时间内，弦的振动范围始终没有超出计算区间，则认为其为周期性边界条件；然而，当波动时间持续向前推进，弦的振动范围到达计算区间边界。此时，波动函数必须满足边界条件，并给波动方程的后续推进带来影响，这也将导致FDM 和FFT 模拟方法的结果呈现一些差异。

设定a= 1,f(x,t) = 0,u(x,0) = 2 sech(x),∂u(x,0)/∂t= 0,u(−40,t) =0,u(40,t)=0。需要指出，这里将前面FFT 理论中：左边界u(0,t)=0 扩展到u(−l,t)=0，右边界u(1,t) = 0 扩展到u(l,t) = 0，其中l= 40。将该模型条件引入公式(1)，可以得到

2.1 FDM 模拟

因为边界条件为u(−40,t)=0,u(40,t)=0，同时f(z,t)=0，则公式(5)变化为

利用有限差分法理论，结合公式(8)和公式(9)，编写FDM 程序并输出结果，如图1 所示。在图1 中，设置模拟时间t= 20 s，可以看到弦的振动范围没有超出计算区间；设定模拟时长为t= 160 s，以观察模拟不同时长情况下的振动状态，模拟结果如图2 所示。图2 中，模拟时间t= 40 s 时，可以看到弦的振动到达计算区间的边界，由于设置边界条件为u(−40,t) = 0,u(40,t) = 0，振动快速降低为0，并随时间的推移向负值传递。同时，为了方便和后续实验进行比较，对图2 的波动方程模拟经行绝对值化处理，结果如图3 所示。

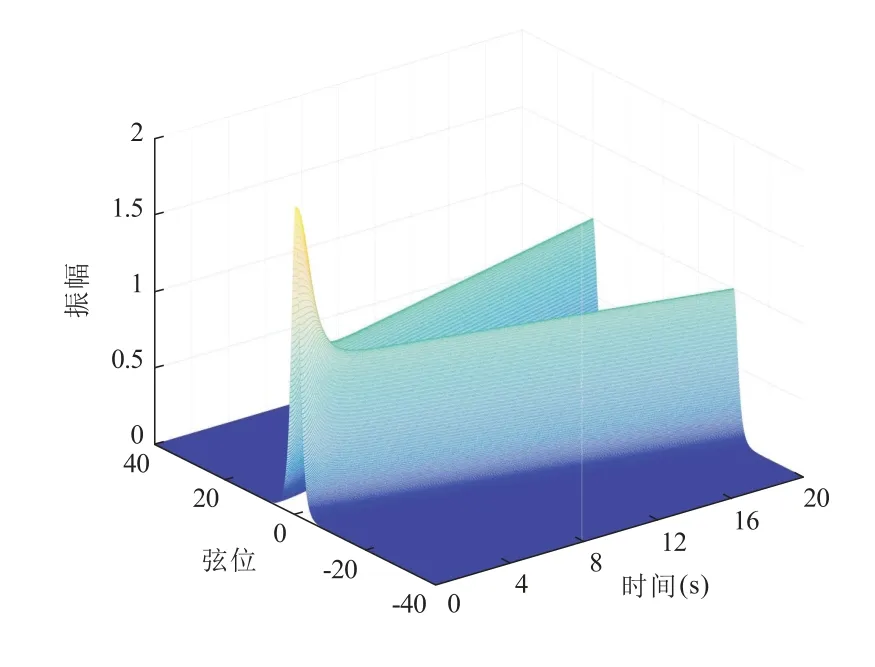
图1 一维波动方程FDM 模拟图(t=20 s)

图2 一维波动方程FDM 模拟图(t=160 s)

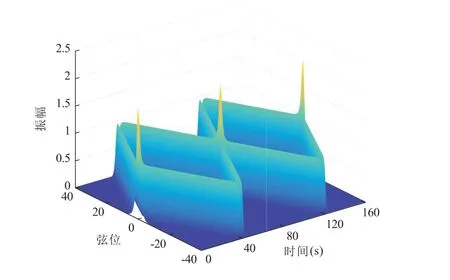
图3 |u|的一维波动方程FDM 模拟图(t=160 s)

2.2 FFT 模拟

对模型公式(8)经行FFT 变换

利用FFT 变换，将波动方程由时域系统的偏微分方程转变为频域系统的常微分方程。转换为频域系统后，初值条件也要转换到频域。由于该模型中初值ut、vt和−k2为向量，采用Simulink 搭建模型时要遵循矩阵运算规则。这样模拟信号经过积分器模块后，得到的输出仍然为向量化信号，如图4 和图5 所示。需要注意的是，积分器模块需要保证入口信号为实数；而频域系统初值ut、vt经过FFT 变换为复数，这就需要对复数特别处理：将复数分为实数和虚数两路信号并做积分运算，然后在IFFT 变换前将两路信号合并为复数信号；这个复数信号在积分前完成四则运算后再分为实数和虚数两路信号进入积分模块入口。经过实验发现，当虚数信号非常小的时候，直接取实数信号作模拟也能得到符合精度要求的模拟结果，这样做的原因是可以节约计算时间的成本，如图6 和图7 所示。这样的系统模型简洁，且不易出错，也易于维护[16]。

图4 一维波动方程的FFT 仿真图(实数域)

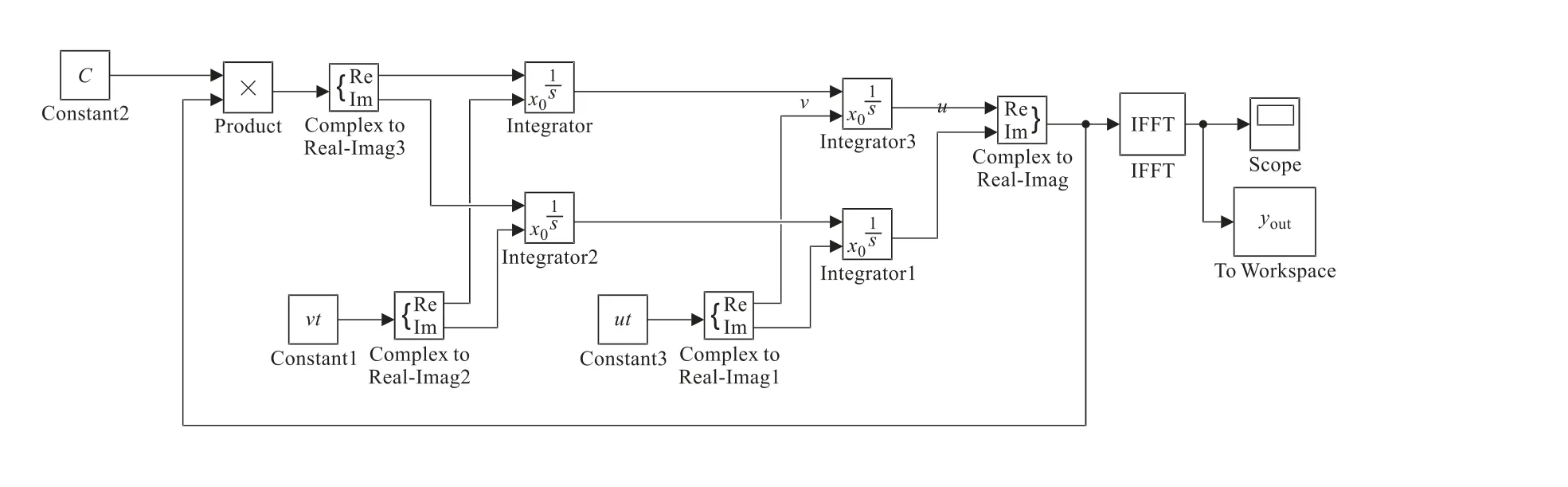
图5 一维波动方程的FFT 仿真图(复数域)

图6 |u|的一维波动方程FFT 模拟图(t=20 s)

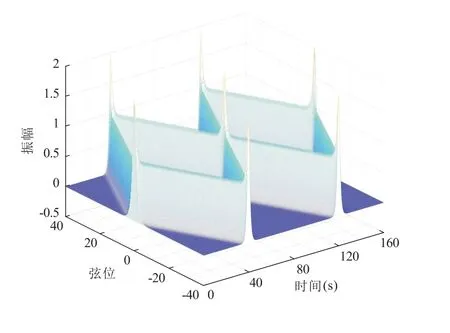
图7 |u|的一维波动方程FFT 模拟图(t=160 s)

对采用FDM 模拟的图1 至图3 和采用FFT 模拟的图6 和图7 进行比较：

1) 比较图1 和图6，模拟时长为t=20 s 时，两个数值方法模拟结果相同；

2) 比较图2 和图7，在函数计算区间边界处且时域t= 40 s 和t= 120 s 两点附近，图2 呈现出递减到0 的趋势，而图7 呈现出突然上扬的趋势；模拟时长为t ∈(40,120)，两个数值方法模拟结果显示数值大小一致，符号相反。其它模拟时长中，两个数值方法模拟结果基本一致；

3) 比较图3 和图7，除去函数计算区间边界处且时域t= 40 s 和t= 120 s 两点附近的差异，两个数值方法模拟结果基本一致。

对于图7 中呈现的突然上扬趋势，由于FFT 算法采用了周期性边界条件，其相当于将该函数强制转化为在边界处间断、周期为L的周期函数。该实验案例中，在时间t= 40 s 和t= 80 s 处，该函数在计算区间的边界附近迅速衰减到0，这时得到的模拟函数会在间断点附近产生震荡，出现吉布斯现象。从图7 和图2 的对比中可以清楚地观察到这一点；对于图7 中模拟时长为t ∈(40,120)函数出现和图2 模式值大小相等符号相反的现象，本文采用对u取绝对值进行处理；同时需要指出的是，对于x的离散方式进行修改，将是改变这种现象的一个思路。

2.3 VOFFLC 时域控制

利用FFT 理论将波动方程时域PDE 方程转化为频域ODE 方程，尝试利用VOFFLC控制器设计实现波动方程频域ODE 系统自适应控制的实验。

2.3.1 反馈信号乘法实验

通过前面对FFT 和成熟FDM 模拟实验结果的对比，说明基于Simulink 平台采用FFT 原理模拟PDE 波动方程的思路可行。在图4 和图5 的的基础上，尝试在IFFT 模块的出口实施一个基于VOFFLC 闭环控制，这里尝试对控制信号进行乘法处理：设定时域期望向量w=2·sin(x)，IFFT 模块出口向量为u；本文给定VOFFLC 控制器入口值的处理规则为(w −u)T(w −u)，以保证进入控制器的量为标量，同时，该规则有进一步优化的需要，有待研究；然后，该标量经过自适应VOFFLC 控制器的处理，进入PDE 波动方程的FFT 模拟系统，和C相乘。尝试对一维波动方程的VOFFLC 时域控制仿真，如图8 和图9 所示。

图8 一维波动方程的VOFFLC 控制的乘法实验仿真图(实数域)

图9 一维波动方程的VOFFLC 控制的乘法实验仿真图(复数域)

设定时域期望向量w= 2·sin(x)，模拟时长为t= 20 s 和t= 160 s，其模拟结果如图10 和图11 所示。

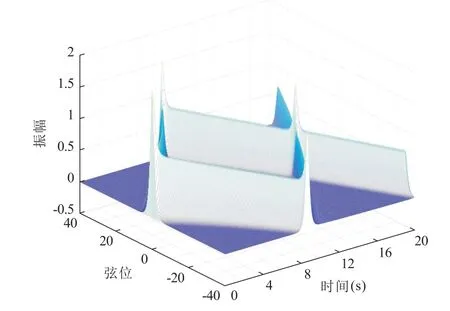
图10 一维波动方程的VOFFLC 控制的乘法实验模拟图(t=20 s)

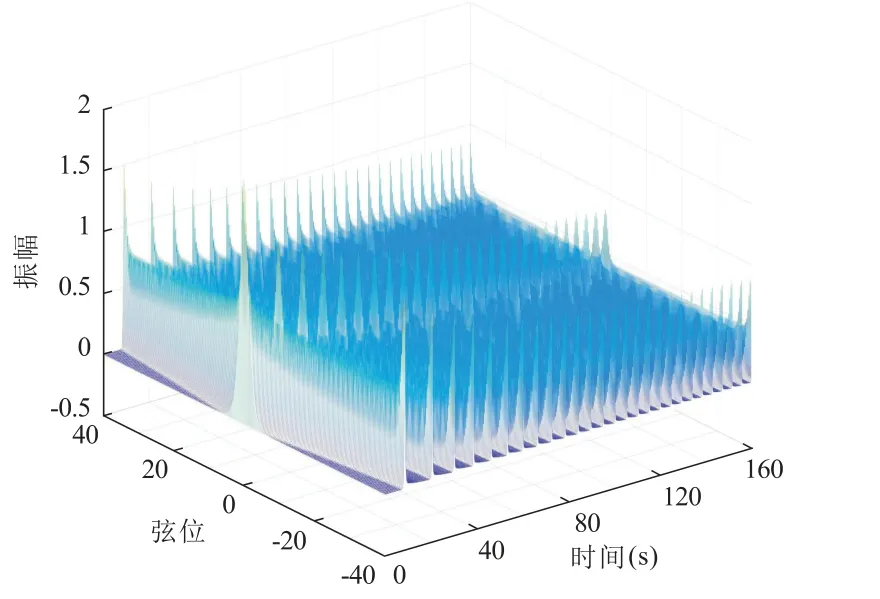
图11 一维波动方程的VOFFLC 控制的 乘法实验模拟图(t=160 s)

对图10 和图11 和图7 进行比较：

1) 比较图10 和图7，模拟时长为t=20 s 时，波动形态一致，图10 周期缩短；

2) 比较图11 和图7，模拟时长为t= 160 s 时，波动形态一致，图11 周期缩短的速率加快，且u的值随时间的增加在逐渐的减小。

由上述现象来看，虽然该乘法实验表现出一定的规律，但是并没有达到时域控制的基本要求。

2.3.2 控制条件为0 的反馈信号减法实验

基于上述一维波动方程的VOFFLC 时域控制的乘法实验，做出修正：设置时域控制条件为0，为了程序实现将其离散为w= 0·sin(x)，IFFT 模块出口向量为u；给定VOFFLC 控制器入口值的处理规则同上；然后，经过自适应VOFFLC 控制器的处理，进入PDE 波动方程的FFT 模拟系统，和C相减，模拟时长为t=20 s 和t=100 s。构建模拟仿真图12，尝试对一维波动方程的VOFFLC 时域控制仿真，结果如图13 和图14 所示。

图12 一维波动方程的VOFFLC 控制的减法实验仿真图(实数域)

图13 一维波动方程的VOFFLC 时域控制的模拟图(t=20 s)

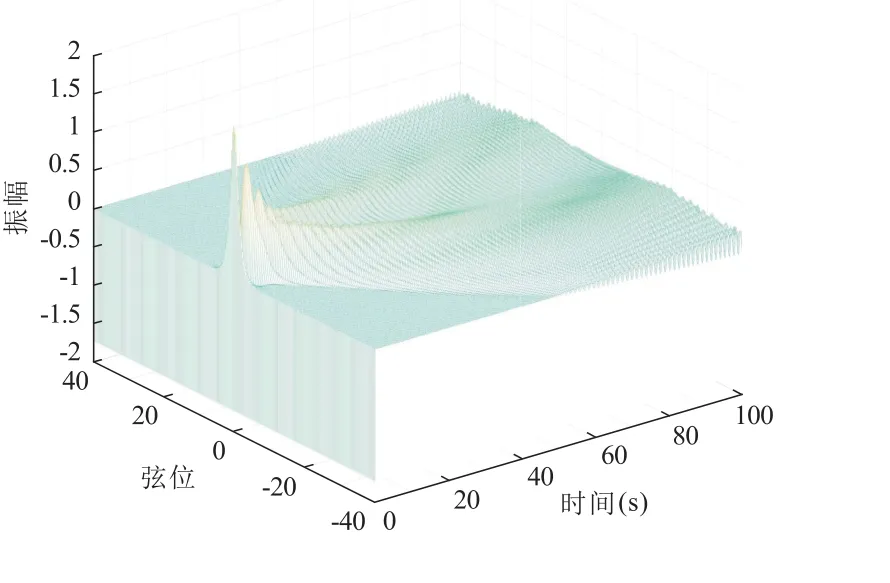
图14 一维波动方程的VOFFLC 时域 控制的模拟图(t=100 s)

对图13、图14 和图7 进行比较：

1) 比较图13 和图7，模拟时长为t=20 s 时，图13 出现类似水纹能量衰减的震荡，且为逆向圆弧的形状；

2) 比较图14 和图7，模拟时长为t= 100 s 时，图14 类似水纹能量衰减震荡，向远方趋于停止震荡，直到静止为0。

由上述现象来看，控制效果更加清晰，可以认为VOFFLC 达到时域控制的基本要求。

2.3.3 控制条件为w=2·sin(x)的反馈信号减法实验

设置控制条件为w= 2·sin(x)，模拟时长为t= 20 s 和t= 100 s，结果如图15 和图16 所示。

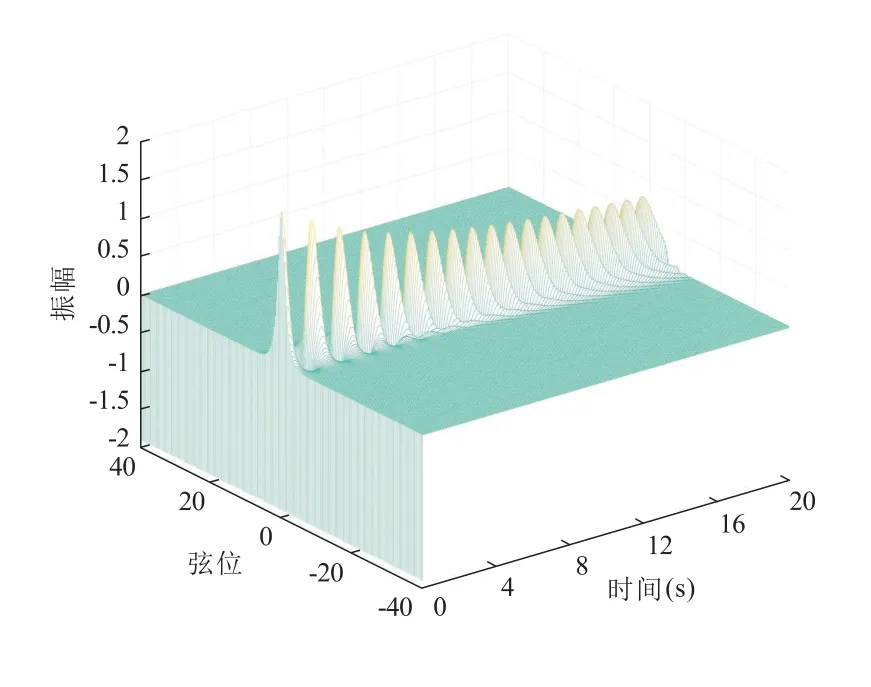
图15 一维波动方程的VOFFLC 控制的 减法实验模拟图(t=20 s)

图16 一维波动方程的VOFFLC 控制的 减法实验模拟图(t=100 s)

对图15、图16 和图7 进行比较：

1) 比较图15 和图7，模拟时长为t=20 s 时，图15 的波形呈现正弦化的趋势，且没有呈现快速向边界振动的趋势；

2) 比较图16 和图7，模拟时长为t= 100 s 时，随着时间的推移，波动在呈现正弦化的同时，趋于正弦形态的稳定。

由上述现象来看，VOFFLC 达到时域控制的基本要求。

3 结论

通过以上实验，总结出一些需要进一步处理的问题：

1) 由于FFT 方法采用周期性边界条件，将函数从时域函数强制转化为在边界处间断、周期为L的频域周期函数，当波动震荡到计算边界时，会在边界间断点产生震荡且出现吉布斯现象，并在通过边界后的时间里影响到波动的数值符号，因而需要采取进一步的改进措施并作实验验证。同时，对边界函数不为0 的条件，在使用FFT 变换的时候需要补充处理规则；

2) 文中为保证进入控制器的参数从向量变为标量，设计VOFFLC 控制器入口值的处理规则为(w −u)T(w −u)；然而从控制效果来，实现控制条件的见效时间比较长，需要作进一步的优化；

3) 从图8 可知，波动方程仿真系统的状态变量为256 元素的向量且在经过FFT 变换后由实数域变成复数域。因此，在Simulink 中模拟而模拟步长较小时就会出现仿真速度慢且数据庞大的弊端；而从本文案例来看，虚数域可以技术性舍弃；因此，如何界定虚数域舍弃标准和设计高效复数域计算算法，需要进一步的研究。

然而，实验也取得了一些有用的发现：

通过FDM 模拟结果的比较验证，基于Simulink 平台实现了利用FFT 方法将波动方程从空域PDE 模型转化为频域ODE 模型，并在频域上搭建类似于集中参数的控制系统，实现的方法是在频域ODE 模型出口添加IFFT 模块，这样IFFT 出口参数将被转换成原来时域上的波动函数，再对波动函数施加自适应VOFFLC 闭环控制，并给定VOFFLC 控制器入口值的处理规则为(w −u)T(w −u)，以保证进入控制器的参数从向量变为标量；然后对控制型号的处理采用了乘法和减法两种反馈法则。

其中，采用乘法法则的VOFFLC 控制时，波动呈现了和原来的形态一致，而周期缩短和振幅减小的现象。而采用减法法则的VOFFLC 控制时，设计时域控制条件为w= 0·sin(x)时，波动呈现类似水纹能量衰减的震荡且为逆向圆弧的形状，并向远方趋于震荡减弱直到静止为0，可以实现类似边界控制的结果；设定时域控制条件w=2·sin(x)时，随着时间的推移，波动在呈现正弦化的同时，趋于正弦形态的稳定，可以在空间维度(x轴)上实现向量级控制，即对x轴任意函数形状、插值函数或者散点的向量级别控制，这个是边界控制做不到的。因而，基于FFT 的波动方程VOFFLC 控制有进一步的研究意义和广阔的实用价值。