基于多尺度Transformer的多视图三维形状分析方法

卫 鑫, 孙 剑

(西安交通大学数学与统计学院，西安 710049)

0 引言

三维形状分析是计算机视觉领域中最基础且重要的问题之一，在众多应用中发挥着关键的作用，例如自动驾驶[1–2]、考古学[3]、生物学[4]、虚拟现实和增强现实[5]等。三维形状分析的核心挑战之一是如何获取三维形状的有效特征表示。根据三维形状的不同表示方法，基于深度学习的三维形状分析方法可分为三类：基于体素的方法、基于点云的方法和基于多视图的方法。基于体素的三维形状分析方法[6–7]直接在规则的三维体素网格上进行操作，与传统的二维卷积神经网络(Convolutional Neural Network, CNN)具有一定的相似性。尽管这些方法通常能够获得较好的结果，但它们常常受到计算复杂度和数据稀疏性的限制。相比之下，基于点云的三维形状分析方法[8–13]以无序的点集作为输入，使用点云处理网络来输出三维形状的类别。与其他两种方法不同，基于多视图的三维形状分析方法[14–20]使用二维图像特征的集合来进行三维形状的分类，能够充分利用深度学习在二维图像特征提取方面的强大能力，通常在三类方法中表现出最佳的性能。因此，本文利用基于多视图的方法进行三维形状的分析与研究。

在基于多视图的三维形状分析中，一项主要挑战是如何有效地将多视图特征聚合以获得一个强有力的全局三维形状描述符。传统方法，如MVCNN[14]和GVCNN[15]，使用最大池化来聚合多视图的特征，这种方法虽然保证了排列不变性，但忽略了视角之间的空间关系，从而导致学习到的特征丢失了一部分判别能力。而VERAM[16]将多个视图建模为序列，使用循环神经网络(Recurrent Neural Network, RNN)处理多视图特征。View-GCN[17]和View-GCN++[18]则提出使用视角图来建模多视图之间的关系，并设计了图卷积神经网络来探索多视图之间的关联性。

另一方面，基于Transformer[21]的多视图三维形状分析方法，如CVR[19]和MVT[20]，利用Transformer 在建模集合关系上的强大能力，使用Transformer 编码器来建模多视图之间的关系。然而，这些方法在建模多视图关系时忽略了不同视图的投影视角坐标所蕴含的空间关系，仅仅使用具有全局感受野的Transformer 编码器对多视图特征进行处理。

在实际中，根据View-GCN[17]提出的理论，投影视角坐标中蕴含的信息编码了三维物体的潜在几何形状，为形状识别提供了有价值的线索。通常情况下，投影视角坐标距离越近的图像，应当具有更相似的特征。如果多个相邻连续投影视角下的图像是相同的，那么该物体更可能是一个圆柱形的水杯，而不是一把椅子。因此，利用投影视角坐标的距离来调整Transformer 感受野的范围，能够获得比全局Transformer 更精细的特征表示。然而，如何确定感受野的大小仍然是一个需要解决的问题。使用较小的感受野可能只能捕捉到视角关系的局部信息，丧失了如对称性等全局的信息，而使用较大的感受野可能导致特征变得过于复杂，视角关系的学习难以处理。

为了解决上述问题，受到多尺度学习方法[22–24]的启发，本文提出了一种新的基于多尺度Transformer 的多视图三维形状分析方法(MVMST)，用于更有效地聚合多视图特征。该方法引入了多个不同尺度感受野的Transformer，允许多视图特征同时获得大范围全局信息和小范围局部细节信息。如图1 所示，MVMST 由特征提取骨干网络、多尺度Transformer 模块、多尺度融合模块和视角池化模块四部分构成。三维形状的多视图首先经过一个特征提取骨干网络，生成各个视角下的多视图特征。然后，多个不同尺度感受野上的Transformer 分别对多视图特征进行处理。不同尺度下的多视图特征通过多尺度融合模块进行融合，生成一个更为丰富的多尺度表示。最后，通过视角池化模块，每个视角下的特征被整合为三维形状的整体特征表示。本研究的主要贡献总结如下：

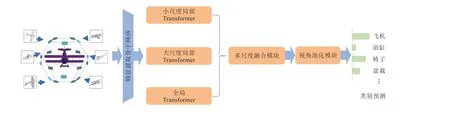
图1 MVMST 的主要结构

1) 引入了投影视角坐标的距离作为Transformer 感受野的限制，更好地建模了多视图特征之间的局部关系；

2) 提出了一种基于多尺度Transformer 的三维形状分析方法，充分利用大尺度感受野Transformer 和小尺度感受野Transformer 在处理多视图特征的优势，将多尺度Transformer 处理后的多视图特征融合为一个更为有效的整体形状表示；

3) 在人工合成和真实扫描的三维形状分类数据集上进行实验，证明了本文所提出的方法在三维形状分类问题中具有令人满意的性能。

本文的结构如下：首先，在第1 节中回顾了基于多视图的三维形状分析和计算机视觉中的Transformer 网络的相关工作；第2 节介绍了基于多视图的三维形状分析问题的设置以及本文所提出的基于多尺度Transformer 的多视图三维形状分析方法的具体结构；第3 节对基于多尺度Transformer 的多视图三维形状分析方法在多个三维形状分类数据集上进行了实验；第4 节总结了本文的主要思想和方法。

1 相关工作

1.1 基于多视图的三维形状分析

基于多视图的三维形状识别方法使用二维卷积神经网络对渲染的三维形状的图像进行卷积，能够在不依赖复杂的三维特征的情况下实现出色的性能。最早的工作MVCNN[14]方法开创性地使用二维卷积神经网络来提取每个视图的特征，然后通过最大池化层融合特征以生成全局描述符。在MVCNN 的基础上，GVCNN[15]对视图进行分组，为包含更多关键信息的组分配更高的权重，并据此融合所有组的特征，生成全局描述符。另一个值得注意的工作是3D2SeqViews[25]，它通过聚合连续视图来学习三维全局特征。View-GCN[17]和View-GCN++[18]则通过图卷积神经网络逐层融合不同视图之间的特征。RCPCNN[26]也将视图分为多个组，并将各组的特征串联以生成全局描述符。RN[27]通过在网络中引入特征增强模块，使用来自所有视图的信息增强每个图像块的特征。MHBN[28]探索了如何聚集图像块级特征，将三维形状识别问题转化为集合对集合的匹配问题。MVT[20]和CVR[19]则利用Transformer 进行视角特征之间的信息交互。这些基于多视图的三维形状识别方法在不同程度上利用了多视图信息，结合了二维卷积神经网络和其他技术，以生成高效的全局描述符。与上述方法相比，本文在多视图三维形状分析中引入了一种全新的方法MVMST，通过多尺度Transformer 来进行特征聚合，更好地捕获多视图特征之间的关系。具体而言，MVMST 引入了多个不同大小感受野的Transformer，并设计了多尺度融合模块对不同尺度的多视图特征进行融合，这有助于细致地描述三维形状多视图之间的关系，从而提高了全局描述符的表达能力。

1.2 计算机视觉中的Transformer 网络

得益于Transformer[21]在自然语言处理领域取得的巨大成功，只依赖于Transformer模块的无卷积模型在计算机视觉领域中也得到了长足的发展。其中ViT[29]是第一个将Transformer 应用在图像分类的方法，证明了Transformer 在计算机视觉领域可以与卷积神经网络相媲美，甚至具有超越的潜力。之后的一系列改进的方法[30–33]进一步提升了Transformer 模型的性能和计算速度。相比于卷积神经网络，Transformer 网络可以通过自注意力机制自然而然地获取远距离信息，建模图像的全局关系。该优势同样体现在基于多视图的三维形状识别任务中。CVR[19]和MVT[20]使用Transformer 来建模多视图特征之间的关系，然而他们都是用Transformer 在全局上处理所有视角图的特征，没有考虑到不同视角图的投影视角坐标在空间上蕴含的关系。与CVR[19]和MVT[20]不同，本文根据投影视角的空间关系定义了多个不同尺度感受野下的Transformer 模块，使得学习到的多视图特征既包含大尺度的全局信息，又包含小尺度的局部细节信息。

2 基于多尺度Transformer 的多视图三维形状分析方法

2.1 问题设置

2.2 方法框架

本节介绍基于多尺度Transformer 的多视图三维形状分析方法(MVMST)。如图1 所示，MVMST 由四个主要模块组成，包括特征提取骨干网络、多尺度Transformer 模块、多尺度融合模块和视角池化模块。对于输入的三维形状的多视图图像，首先，使用特征提取骨干网络分别提取其特征。随后，多尺度Transformer 根据多视图之间的关联性，对不同尺度下的多视图特征进行处理和融合。紧接着，多尺度融合模块将不同尺度下的多视图特征进行融合。最终，通过视角池化模块，生成一个全局形状描述符。在接下来的2.2.1、2.2.2、2.2.3 和2.2.4 小节中，将详细介绍这四个模块的设计细节。

2.2.1 特征提取骨干网络

给定N个不同视角下的多视图图像{Ii}Ni=1以及它们对应的视角{vi}Ni=1，特征提取骨干网络E提取多视图特征{fi}Ni=1，其中fi=E(Ii;θE)，特征fi是d维向量，参数θE在所有视角之间共享。为了在性能和计算速度之间取得平衡，特征提取骨干网络E采用ImageNet 上经过预训练的卷积神经网络ResNet-18。多视图{Ii}Ni=1在经过ResNet-18 的最后一个全连接层之前的特征，向量化后被定义为视图特征。

2.2.2 多尺度Transformer 模块

在介绍多尺度Transformer 的具体结构之前，首先，给出Transformer[21]的基本定义。在本文中，我们使用Transformer 编码器来处理多视图特征矩阵F，矩阵F ∈RN×d的行向量是集合{fi}Ni=1中的d维向量。在Transformer 编码器中，查询矩阵、键矩阵和值矩阵都是多视图特征矩阵F经过线性变换得到的。具体而言，查询矩阵Q、键矩阵K和值矩阵V可以被定义为

这里的WQ ∈Rd×d,WK ∈Rd×d以及WV ∈Rd×d，都是可以学习的参数矩阵。Q、K和V上的自注意力机制可以定义为

基于自注意力机制，Transformer 编码器可以进一步定义为

其中headh=Attention(Q,K,V)，Concat 为矩阵串联操作，将h个N×d维度的矩阵串联为N×hd维度的矩阵，WO ∈Rdh×d也是一个可学习的参数矩阵，将d·h维的多视图特征映射回d维。

在Transformer 编码器的基础上，本工作提出了使用投影视角坐标的距离来定义不同尺度下的Transformer 模块，以学习不同尺度下视角之间的关系信息。考虑多视图特征矩阵F ∈RN×d和视角坐标矩阵V ∈RN×3，可以定义一个掩码矩阵M ∈RN×N，矩阵M的元素定义如下

其中k-NN 代表k-最近邻，用于寻找与给定视角坐标vi在视角空间中欧氏距离最接近的k个视角坐标。I(·)是一个指示函数。通过计算视角之间的欧氏距离，掩码矩阵M用于标识视角vi的k个最近邻居，这有助于捕捉不同视角之间的关联性。具体来说，掩码矩阵M的元素Mij表示了视角vj是否位于视角vi的k个最近邻之内。如果是，则Mij为1，否则为0。在多尺度Transformer 模块中，我们使用不同的k值来控制不同尺度下的关系建模。较小的k值可以实现更局部的关系建模，而较大的k值则可以捕获全局的关系。这允许我们在不同尺度下灵活地探索视角之间的关系，以获得更丰富的特征表示。因此，k尺度下的Transformer 编码器可以定义为

其中⊙表示两个矩阵的哈达玛积操作。以上方法将Transformer 的自注意力机制限制在一定尺度视角范围内，从而更好地捕捉不同尺度下的视角关系信息。

总而言之，基于Transformer 编码器和投影视角坐标的距离关系，我们引入了多尺度Transformer 模块，用于学习不同尺度下的多视图特征之间的关系，这有助于更好地理解三维形状并提高三维形状分析的性能。

2.2.3 多尺度融合模块

不同尺度下的特征可以提供关于三维形状从局部细节到全局结构的不同方面的信息。多尺度融合模块将通过多尺度Transformer 处理的多视图特征进行融合，生成更加全面的多尺度表示，是MVMST 中的一个关键组成部分。

在多尺度融合模块中，我们首先获得了多尺度Transformer 处理后的多视图特征矩阵的集合{ˆFk1, ˆFk2,···, ˆFkM}，这些特征分别表示了不同尺度下的关系信息。这些特征需要被合理地融合在一起，以形成一个更加强大和全面的多尺度表示。为了实现该目标，使用一个融合函数P将多尺度Transformer 处理后的多视图特征进行尺度融合

其中Concat 为串联操作，将M个N×d维度的矩阵串联为N×Md维度的矩阵。P为一个两层的多层感知机，其中的非线性激活函数为LeakyReLU，隐层节点数为d。多尺度融合模块可以合理地整合多尺度信息，从而提高多尺度表示的质量和表达能力。

2.2.4 视角池化模块

视角池化模块将多尺度特征融合后的表示进一步处理，生成最终的全局形状描述符，以便网络能够做出关于整体三维形状的决策。本文使用一种常见的多视图最大池化层对多视图特征进行融合

其中maxpool 代表跨视图的逐元素最大化操作，这种方法能有效地从多个视图中提取最显著的特征，最终输出d维向量Fglobal。全局形状描述符Fglobal是对整个三维形状的综合表示。这个描述符包含了来自多视图和多尺度信息的关键特征，它是网络用于进行三维形状分类、检索或识别的基础。

2.3 损失函数

全局描述符Fglobal被送入一个分类器Cψ和一个softmax 层，最终的损失函数定义为

其中y是类别标签的一个one-hot 编码，即将每个类别标签转换成一个C维的二进制向量，其中只有一个1 表示当前类别，其他位置都是0。

3 实验及对比分析

3.1 数据集

ModelNet40 ModelNet40[34]是由普林斯顿大学的研究人员提供的一个最常用的三维形状分类数据集，包含40 个类别共计12 311 个人工合成的三维形状，其中9 843 个形状用作训练，2 468 个形状用于测试。大量的基于各种表示的方法在该数据集上进行了三维形状分类实验，并报告了各自的结果。

ScanObjectNN ScanObjectNN[35]是三维形状分类另一个常用的数据集，包含15 个类别共计2 902 个不同的三维形状，其中80%用作训练集，20%用作测试集。与ModelNet[34]相比，ScanObjectNN[35]中的三维形状是由三维传感器在真实场景进行扫描获取的。

3.2 实现细节

训练细节：在所有实验中，我们在NVIDIA 3090 显卡上对网络进行了60 轮训练，批量大小为20，每个批次包含20 个形状和对应的400 张多视图图像。在训练神经网络的时候，本文采用的优化算法是使用动量的随机梯度下降算法，初始学习率为0.001，学习率按照余弦退火的方式在60 轮的周期后降至0.000 01。动量设置为0.9，权重衰减设置为0.001。

3.3 实验结果

表1 展示了多种基于多视图的三维形状识别模型在ModelNet40[34]和ScanObject[35]数据集上的分类结果，模型的性能评价指标为逐类别准确率和全局准确率。本文所提出的基于多尺度Transformer 的多视图三维形状分析方法(MVMST)在多个实验数据集上的表现可与其他现有方法进行有力的比较。我们的方法旨在克服多视图三维形状分析中的核心挑战，即如何更好地整合多视图信息和多尺度信息以实现更准确的三维形状分类。

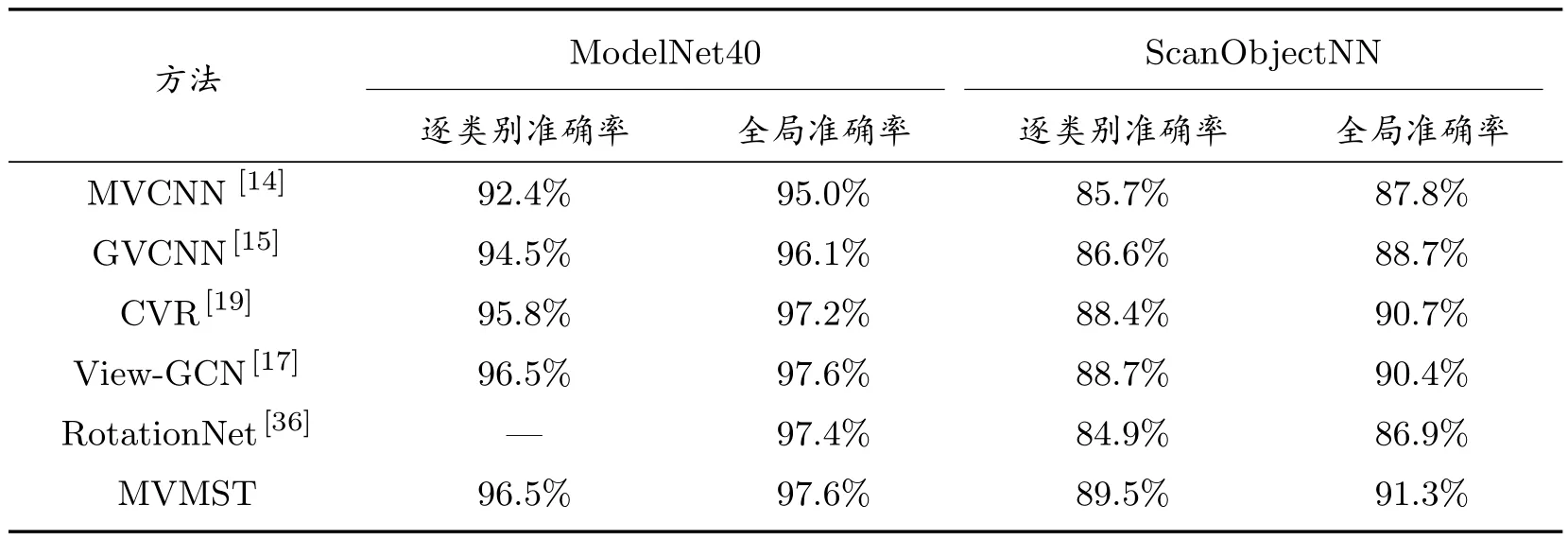
表1 多种基于多视图的三维形状识别方法在ModelNet40 和ScanObjectNN 数据集上的分类结果

首先在常见的合成三维形状数据集ModelNet40[34]上，可以看到MVMST 达到了与View-GCN[17]相媲美的最高逐类别准确率和全局准确率(96.5%和97.6%)。与其他方法相比，MVMST 的性能表现突出，尤其在逐类别准确率方面。这意味着MVMST 能够更好地识别不同类别的三维形状，具有更高的分类精度。我们还将其与经典的MVCNN[14]方法进行了详细的比较。MVCNN[14]作为本方法的基准方法，是多视图三维形状分析领域的一个重要代表。MVMST 在逐类别准确率和全局准确率方面都显著优于MVCNN，分别提升了4.1%和2.6%，这进一步说明了本方法中设计的多个模块的有效性。进一步，在更为复杂的人工扫描三维形状ScanObjectNN[35]数据集上，MVMST 再次表现出色，实现了最高的逐类别准确率和全局准确率(89.5%和91.3%)。相对于其他方法，MVMST 在ScanObjectNN[35]数据集上的性能提高尤为显著，证明了其对于处理具有挑战性的数据集的有效性。

MVMST 的的性能提升归因于其能够有效地学习不同视角之间的关系，将多视图特征聚合为一个更强大的整体描述符。通过引入多尺度Transformer，我们能够充分利用大尺度感受野和小尺度感受野的优势，实现更好的信息融合。同时，我们利用投影视角坐标的距离来限制Transformer 的感受野，以更好地捕捉视角之间的关系。这种方法使MVMST 能够在多视图和多尺度的情况下更好地建模三维形状，提高了分类性能。因此，MVMST 是一种有效的多视图三维形状分析方法，能够在多个数据集上展现出卓越的性能。它对于解决三维形状分类问题具有重要的实际意义，并为未来的三维计算机视觉研究提供了有力的参考。

4 结论

本文针对基于多视图的三维形状识别问题提出了一种新的方法，该方法使用多尺度Transformer 在不同尺度上对三维形状的多视图特征之间的关系进行建模。通过引入多尺度Transformer 和利用投影视角坐标的距离来限制Transformer 的感受野，MVMST 能够更好地捕捉不同尺度和视角之间的关系，从而实现更强大的特征表示。本文在多个三维形状分类基准数据集上对该方法进行了验证，结果表明本方法能够有效的将多视图的特征聚合为一个具有良好表征能力的整体表示符，在分类任务上达到了优于大部分方法的性能。这些结果证明了MVMST 在多视图三维形状分析中的有效性，并为未来的研究提供了一定的启发。