低秩张量填充的循环算法
2024-03-04王俊霞郭雄伟王川龙
王俊霞, 郭雄伟, 王川龙,
(1.太原师范学院数学与统计学院,晋中 030619;2.智能优化计算与区块链技术山西省重点实验室,晋中 030619;3.北京交通大学数学与统计学院,北京 100044)
0 引言
张量填充问题是张量研究中最活跃的热点之一。张量填充可以应用于很多领域,如图像恢复[1–2]、信号处理、数据挖掘[3]、机器学习[4]、图像压缩、高阶网络链接分析[5]等。张量填充问题可以表述为
其中A和T都是N-模张量,且每个模的大小相同,rank(A)表示张量A的某种秩,PΩ是集合Ω上的正交投影,Ω是基数等于m的随机子集,其中m是采样元素的个数。所以,当(i1,i2,···,iN)∈Ω时,PΩ(A)的第(i1,i2,···,iN)个元素等于Ti1i2···iN,否则等于0。关于张量的秩的定义并不唯一,如有基于张量Tucker 分解定义的Tucker 秩,基于张量CP 分解定义的CP 秩,Tubal 秩等,并且张量的秩的计算是NP-难问题。Liu 等人[6]首次提出张量核范数的定义,并将模型(1)转化为
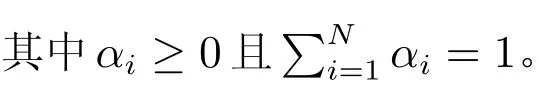
在张量填充的优化算法方面,已有一些研究成果。文献[6]中,Liu 等人给出了张量的核范数的定义,并基于模型(2)提出了三种有效算法:简单低秩张量填充算法(Simple Low Rank Tensor Completion algorithm, SiLRTC)、快速低秩张量填充算法(Fast Low Rank Tensor Completion algorithm, FaLRTC)以及高精度低秩张量填充算法(High accuracy Low Rank Tensor Completion algorithm,HaLRTC)。在文献[7]中,Gandy 等人用张量的秩作为稀疏表示,将其模型转换为更容易求解的凸模型,提出了张量恢复的Douglas-Rachford 分离算法以及交替方向乘子法。Ji 等人[8]基于文献[9],用非凸光滑能量函数logdet(X+εE)替代了张量的秩,提出了如下模型
其中Ei ∈RIi×Ii为单位矩阵,并提出了一种新的求解低秩张量填充问题的算法(LRTCLogdet)。受矩阵填充算法的启发,Tan 等人[10]将张量填充问题化为矩阵填充问题,提出了低多线性秩张量填充算法。为了保持张量原有的内部结构以及避免矩阵化的计算花费,Kilmer 和Martin[11]提出了张量的奇异值分解,且能够很好的保留张量原有的内部结构信息。基于张量的奇异值分解和Tubal 秩的定义,Zhang 等人[12]利用交替方向乘子法框架,给出了相应的算法。此外,还有很多学者研究张量的CP 秩以及基于CP 秩的张量填充算法,详见文献[13–14]。
本文主要研究张量填充问题,基于交替方向乘子法以及子问题循环更新的思想,提出了一种新的张量填充算法,并讨论了该算法的收敛性。通过数值实验,验证了新算法的有效性。
本文的结构安排如下:第1 节介绍张量及矩阵的相关符号说明和定义;第2 节基于交替方向乘子法,运用子问题循环更新的思想,给出了低秩张量填充的循环算法;第3 节给出算法的收敛性分析;第4 节通过数值实验将新算法与HaLRTC 算法、DR-TR 算法及LRTC-Logdet 算法进行了比较;最后,第5 节对全文进行总结。
1 符号说明和定义
本节给出矩阵和张量的相关符号说明及定义。

定义1(奇异值分解)[15]秩为r的矩阵X ∈Rn1×n2的奇异值分解(Singular Value Decomposition, SVD)为
其中U ∈Rn1×r和V ∈Rn2×r是列正交矩阵,σ1≥σ2≥···≥σr >0。
定义2(张量的Tubal 秩)[12]X ∈RI1×I2×I3,对X进行张量奇异值分解(T-SVD),X=U·S·VT,S中非零奇异管的数量称为张量X的Tubal 秩。
定义3(张量展开)[12]张量展开,又称张量矩阵化,是将张量按照一定规律重新排序为矩阵。张量X ∈RI1×I2×···×IN的模-k展开表示为
与其相反的运算定义为foldk(X(k))=X。
2 算法
在这一节中,主要研究张量填充算法。在迭代过程中,通过对子问题的循环更新,减少了在迭代过程中张量展开、矩阵折叠以及奇异值分解的计算花费。
张量填充模型(3)的增广拉格朗日函数为
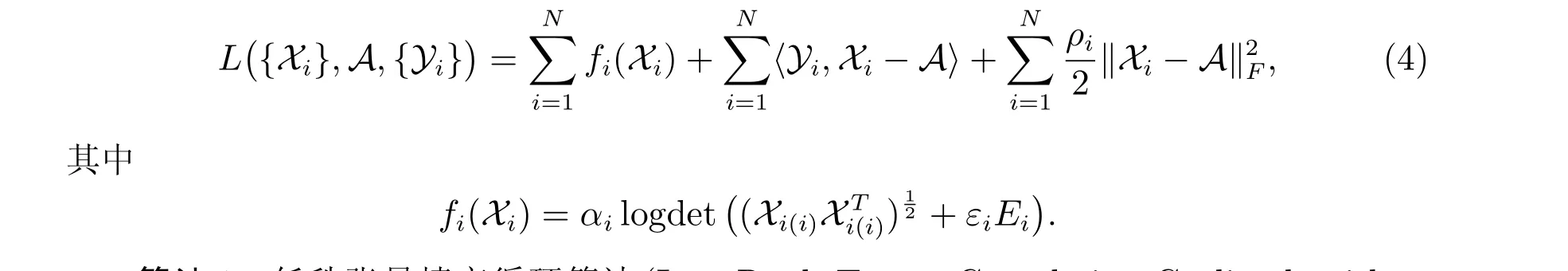
算法1 低秩张量填充循环算法(Low Rank Tensor Completion Cyclic algorithm,简称LRTCC)

引理1 给定矩阵X ∈Rm×n,考虑如下问题

不失一般性,考虑函数

其中ε+wi >0。令g(wi) = (wi −ΣX(i,i))(ε+wi)+τ,利用原函数与其一阶导数的关系,得证。
3 收敛性分析
基于文献[16]提出的关于交替方向乘子非凸问题的收敛性分析,在合理的假设条件下,证明了算法的收敛性。
为表述方便,用s(i)表示变量Xi在第k+1 次迭代前最新的一次迭代。
假设1 给定张量X,Z ∈RI1×I2×···×IN,∀i=1,2,···,N,存在常数Li,满足
其中l{i=Rk+1}为指示函数,即当i=Rk+1时,l{i=Rk+1}=1,否则等于0。
对于给定的参数γi(ρi)及γ,L({Xi},A,{Yi})是分别关于Xi和A的强凸函数。由强凸函数的性质,可得
由子问题的最优性条件,有

上式中,Li是一个常数,ρiγi(ρi)是单调递增的。因此,总可以找到一个足够大的ρi,使得ρiγi(ρi)≥2L2i,∀i=1,2,···,N成立。此时,拉格朗日函数为单调递减函数。
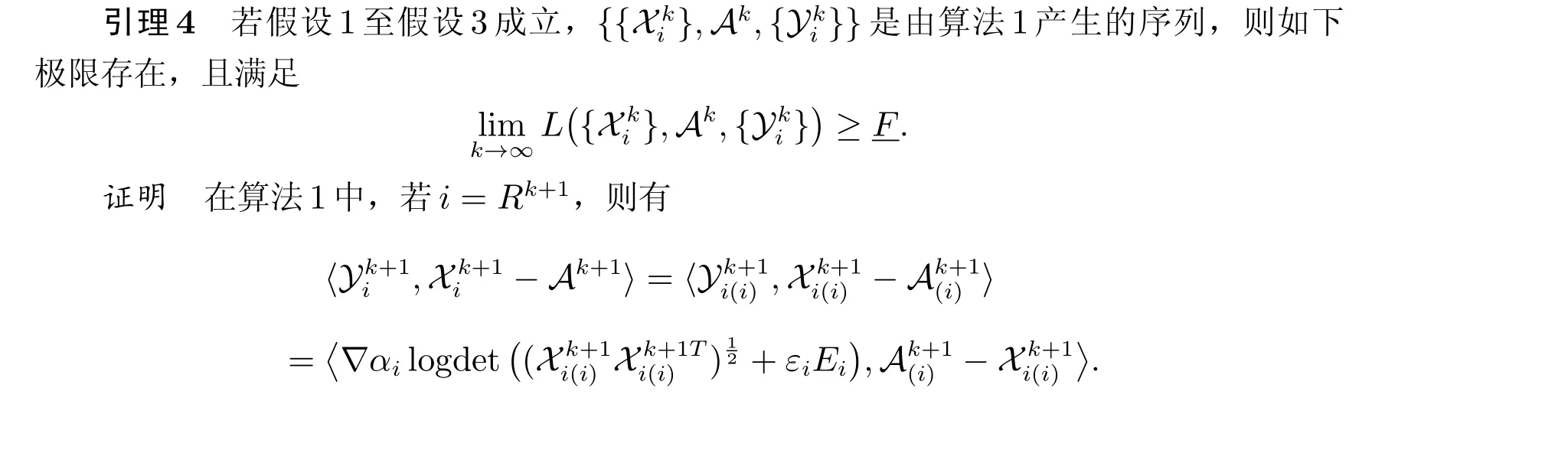
若i/=Rk+1,则根据

定理1 若假设1 至假设3 成立,则有

由于M=N是有限的,且有

4 数值实验
在本节中,通过随机张量填充及图像修复,将低秩张量填充循环算法与HaLRTC 算法、DR-TR 算法及LRTC-Logdet 算法进行比较。所有的数值实验均在Intel(R)Core(TM)i5-1135G7@2.40 GHz,内存16.0 GB,Windows 10 系统下进行,程序在Matlab R2013a上实现。算法1 的参数设置为αi= 1/N,ρi= 10−7,εi= 0.01,t= 1.1,τ=10−7。HaLRTC 算法的参数设置与算法1 相同,DR-TR 算法与LRTC-Logdet 算法的参数,除τ=10−7以外,其余参数分别采取文献[7]和文献[8]的建议。
4.1 随机张量填充
通过随机产生的张量进行算法比较,随机张量通过张量的Tucker 分解生成
其中G ∈Rr1×r2×···×rN是核张量,Un ∈RIn×rn,n= 1,2,···,N为矩阵。实验中,核张量G和矩阵Un由Matlab 中命令randn(r1,r2,···,rN)和randn(rn,In)生成。因此,这样生成的随机张量T ∈RI1×I2×···×IN的秩为(r1,r2,···,rN)。
其中T和A分别表示原始张量和算法输出的最优解。
表1 至表3 为不同采样率下新算法与HaLRTC 算法、DR-TR 算法及LRTC-Logdet 算法的张量填充的实验结果,从表1 至表3 可以看出,在满足误差估计条件下,新算法在时间花费上要明显优于HaLRTC 算法、DR-TR 算法及LRTC-Logdet 算法,体现出新算法的优越性。
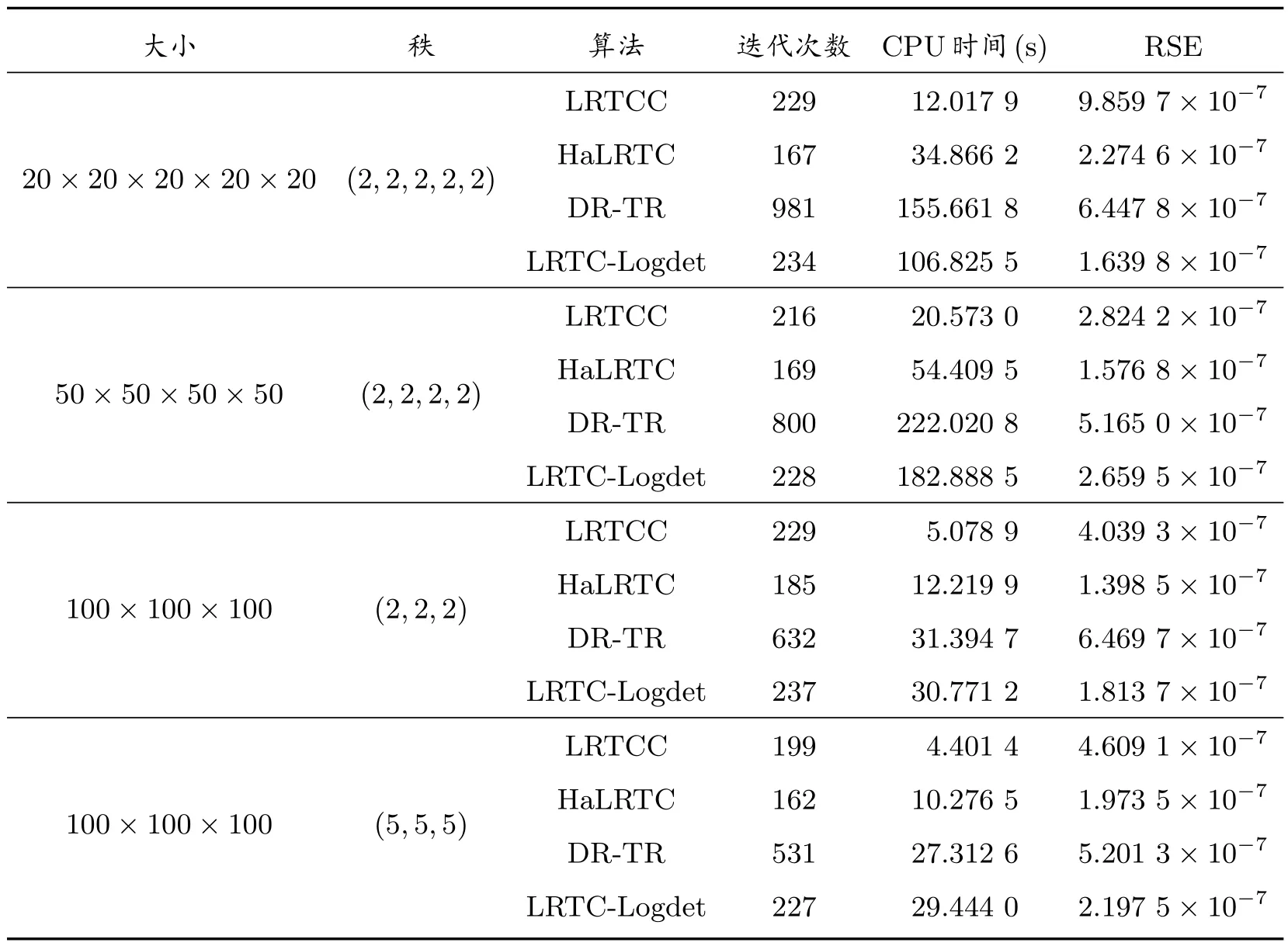
表1 当p=0.2 时,新算法LRTCC 与HaLRTC、DR-TR 和LRTC-Logdet 的比较
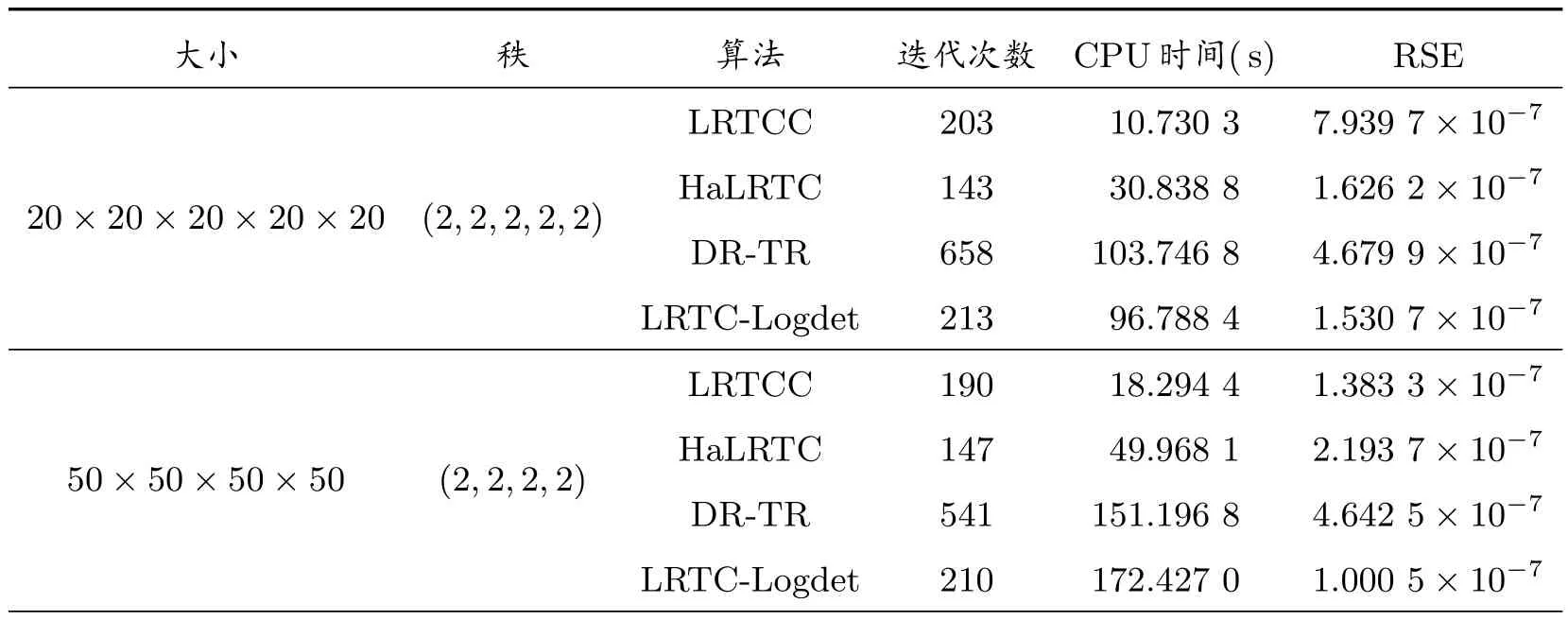
表2 当p=0.3 时,新算法LRTCC 与HaLRTC、DR-TR 和LRTC-Logdet 的比较
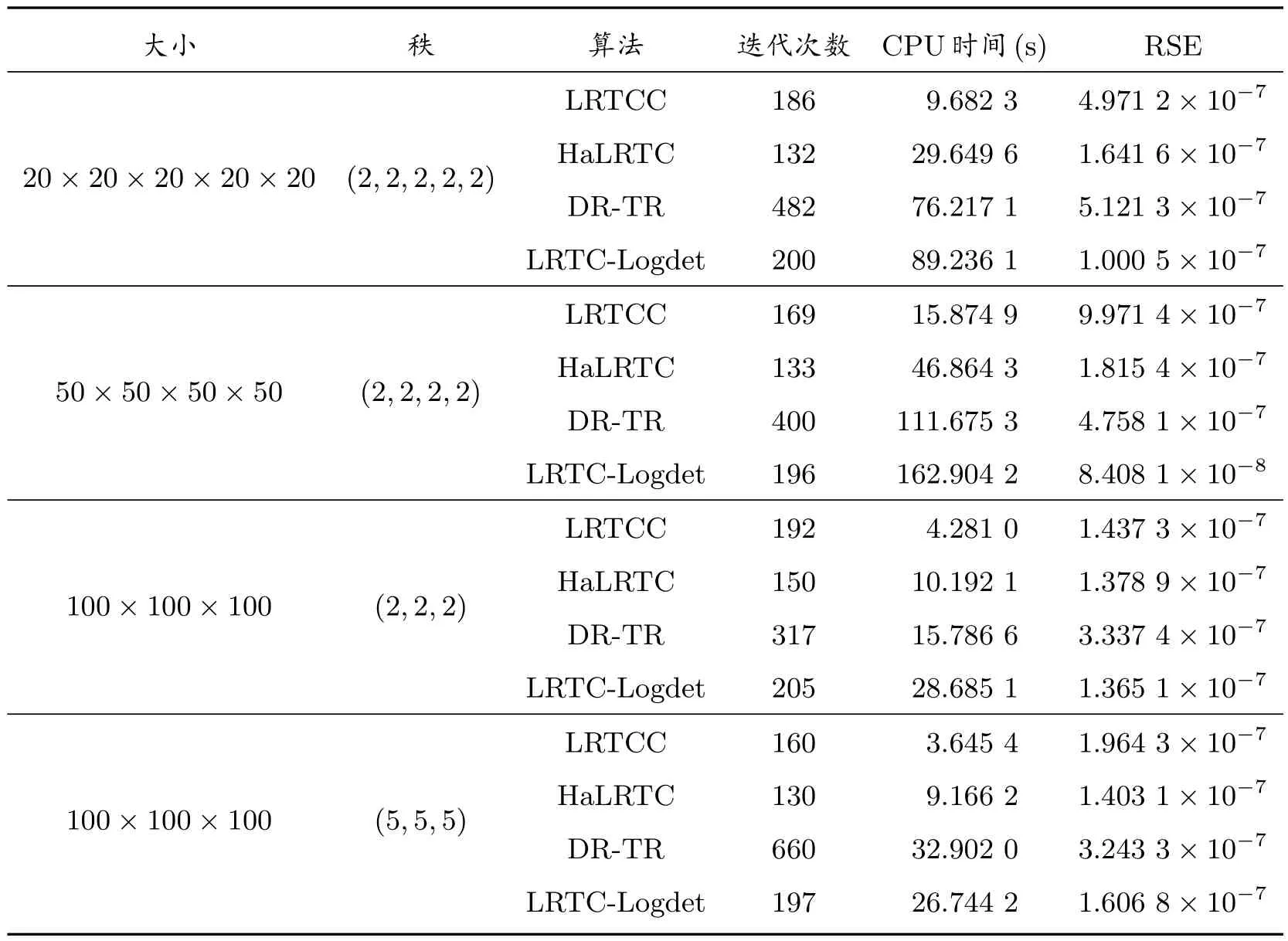
表3 当p=0.4 时,新算法LRTCC 与HaLRTC、DR-TR 和LRTC-Logdet 的比较
4.2 图像修复
使用维数为181×217×181 的MRI 数据比较新算法与HaLRTC 算法、DR-TR 算法及LRTC-Logdet 算法的图像填充效果。为展示其填充效果,随机选取MRI 的某一正向切片,在不同采样率的情况下,其填充效果图见图1 至图6。其中图1 为原始切片图像,图2(a)、图2(b)和图2(c)分别为采样0.2、0.3 和0.4 的图像,图3 为LRTCC 算法修复的图像,图4 为HaLRTC 算法修复的图像,图5 为DR-TR 算法修复的图像,图6 为LRTCLogdet 算法修复的图像。从图1 至图6 可看出,在不同采样率下,四种算法都有较好的图像填充效果。为了体现新算法在时间花费上的优势,在表4 中给出了图像填充的时间花费,并用峰值信噪比(Peak Signal to Noise Ratio, PSNR)体现填充效果,其表达式为
图1 原始切片图像

图2 采样0.2、0.3 和0.4 的图像
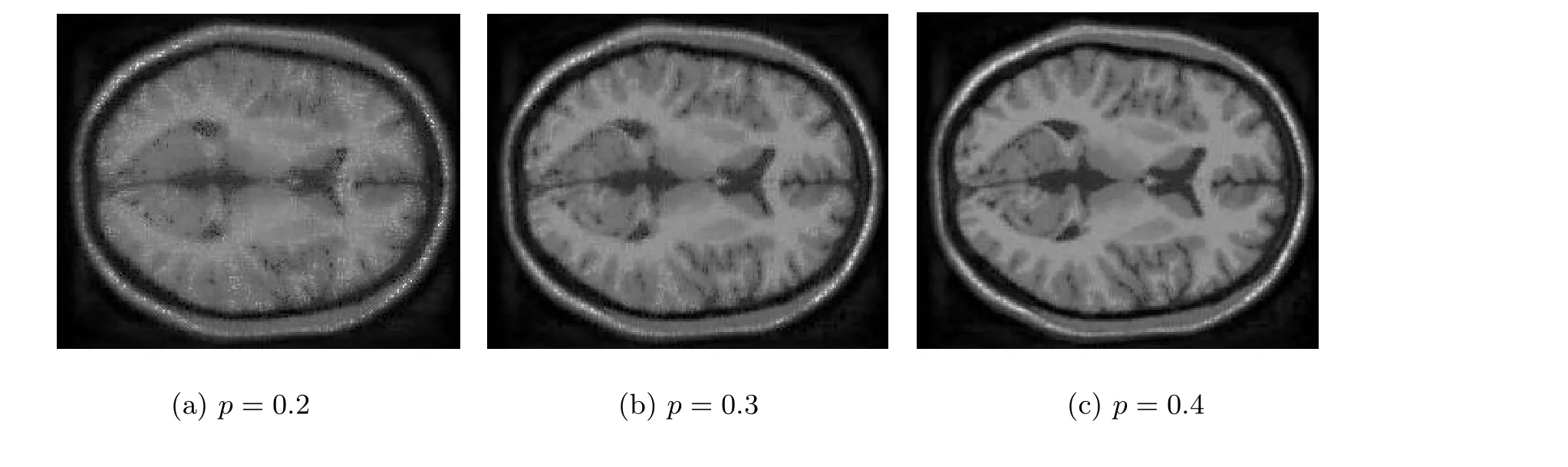
图3 LRTCC 算法修复的图像

图4 HaLRTC 算法修复的图像
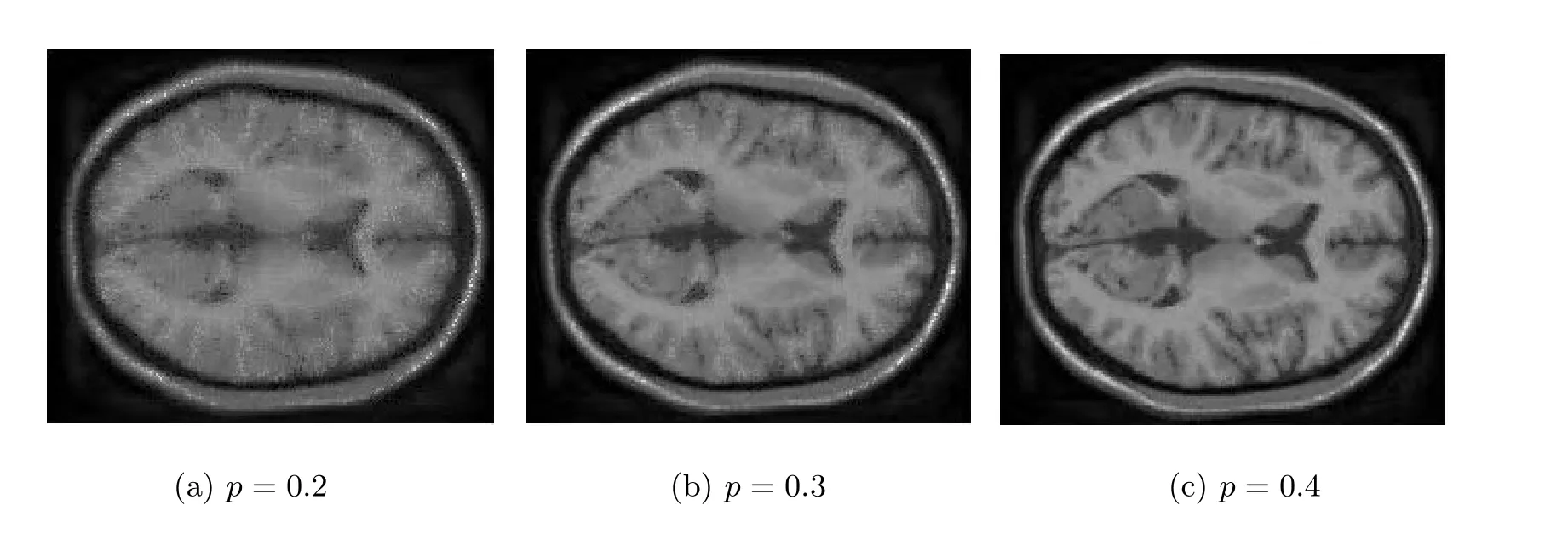
图5 DR-TR 算法修复的图像
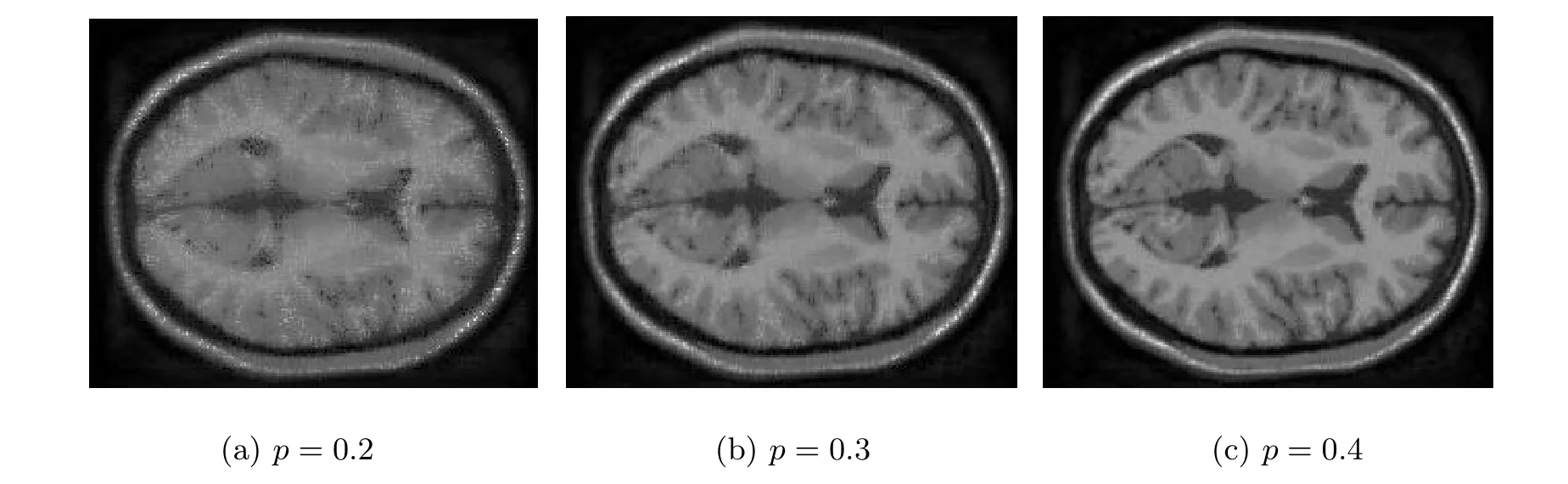
图6 LRTC-Logdet 算法修复的图像
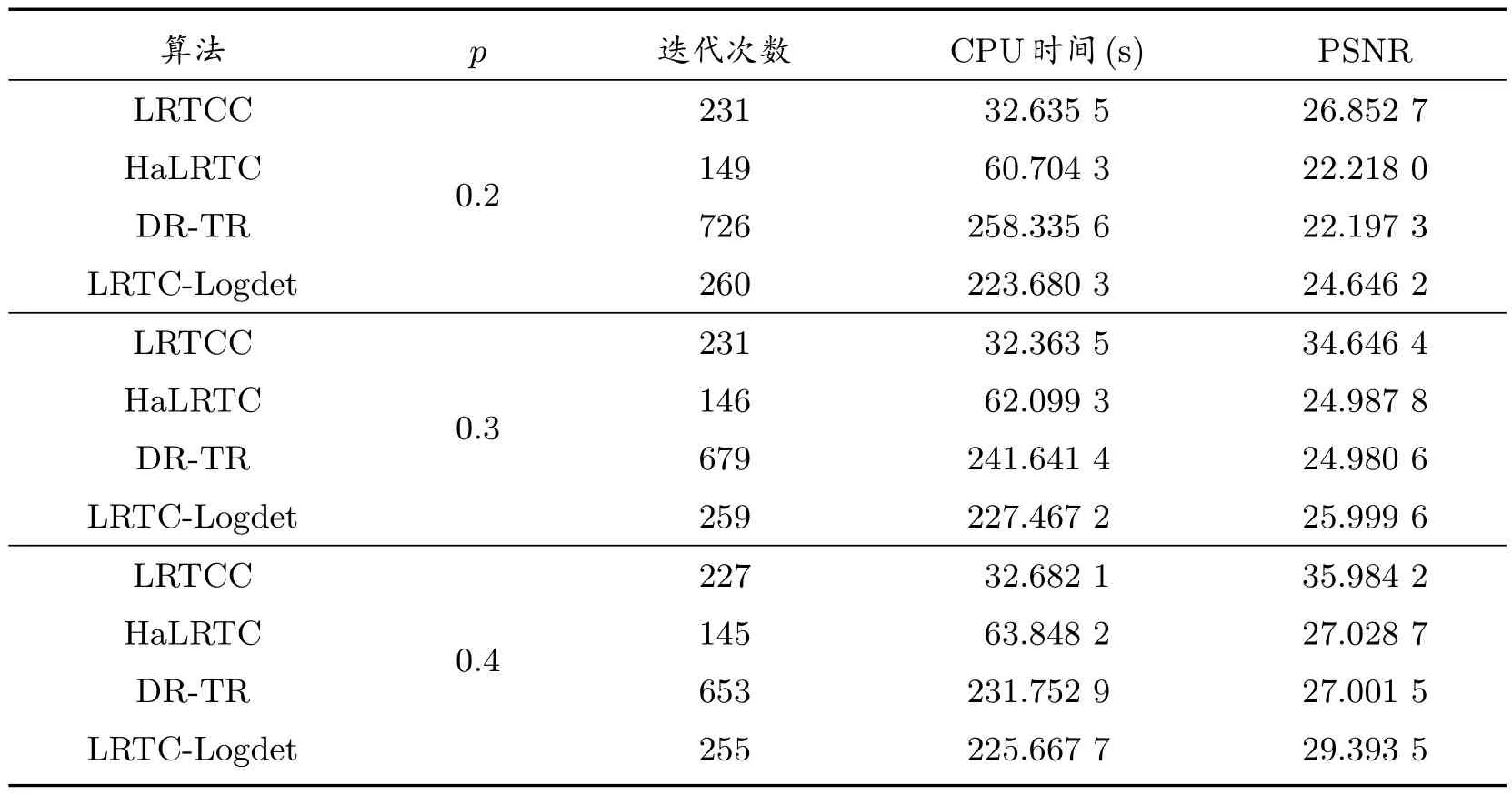
表4 MRI 在不同采样率下的算法比较
其中n表示张量中像素的个数,Tmax表示原始张量的最大像素值。
从表4 中可看出,新算法的时间花费最少,且峰值信噪比值要高于HaLRTC 算法、DR-TR 算法及LRTC-Logdet 算法,进一步验证了新算法的有效性。
5 结论
本文提出了一种新的低秩张量填充算法。该算法基于交替方向乘子法框架,对子问题采取循环更新的方法,减少了在迭代过程中张量展开、矩阵折叠及奇异值分解的计算花费。通过随机张量填充和图像修复试验与HaLRTC 算法、DR-TR 算法及LRTCLogdet 算法进行对比,新算法显示出较强的优越性。
