解题教学:关注学生“五见”意识的培养和强化

杨利刚

(江苏省苏州中学 215007)

解题教学是数学教学中的一个重要组成部分,是教师最为熟悉、最为常用的教学形式之一．数学解题教学是解题活动的教学,解题活动是一种有意识的思维活动,既要有结果也要有过程．解题思路的探求和解答过程的呈现主要反映了思维活动的过程,解题答案主要反映了解题活动的结果．解题教学不仅要获得解题活动的结果(答案),更要呈现解题活动的必要过程,即暴露数学解题的思维活动过程[1],并且让学生积极主动地参与其中、感受其中．

本文中的“五见”是指:思考有主见、审题有预见、答题有远见、卡题有另见、答毕有回见．通过具体的教学实践,笔者以为,在数学解题教学活动中教师是学生思考的引领者、启发者,是学生思维的评价者、调控者;学生是积极主动的思考参与者,是知识内容、数学方法的习得者．教学的本质不仅仅在于传授更在于激励、唤醒、鼓舞,关注学生解题思考中“五见”意识的培养,使学生在解题思考中自发、自觉地领悟,进一步提高数学解题的水平和能力,提升数学素养,促进个体的思维发展．

1 在数学解题思考中,树立主见意识

“学之道,在于悟”,学好数学的关键在于对学习内容和方法的内化与领悟,而不是简单模仿和机械做题．学生应该具有自己的想法、自己的主见(尽管是不太成熟的)．

数学学习强调学生的独立思考和智力参与,形成自己的思考主见.学习的自主性尤为重要,可以说,真正深入、高质量的数学学习必然含有探究的成分[2]．立足于学生的日常学习,教学方法的设计中要特别关注学生的自主性、能动性和创造性,使学生拥有更多的主见和信心．

因此,解题教学中,教学素材要能够自然地吸引全体学生,问题思考能让所有的学生主动参与,学生的学习过程是独立思考基础上的合作交流和相互启发,教学节奏是教师有备而来、张弛适度的科学调控从而渐入佳境．

下面结合一道涉及函数导数不等式恒成立以及求解参数最值的习题教学过程,谈些体会,以期与读者交流切磋．

(2)若关于x的不等式F(x)≤mx-1对任意的x>0恒成立,求整数m的最小值．

2 在数学审题中,唤起预见意识

题目条件提示我们解题应从何处下手、预示“可知”,并启发解题手段．弄清条件就等于弄清行动的起点、明确解题行动的方向．题目的求解结论暗示着求解结果,便于我们在解题过程中进行调整和优化．

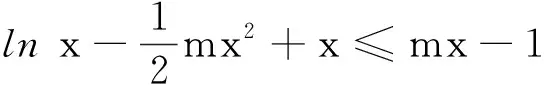
课堂教学中,教师首先引导学生读题分析,明确题意,并且开始初步的独立思考．接下来了解学生的解题想法,得到了如下的初步解题思路．

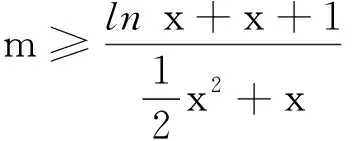
预见瞭望解答过程中避免了对参数m的分类讨论,但回顾以往的解题经历,此做法未必能得到预期结果,最终可能无功而返,比如函数h(x)在区间(0,+∞)上是单调函数(让学生回想之前做过的相关问题,起到预警的作用)．

(1)若m≤0时,φ′(x)>0,则函数φ(x)是(0,+∞)上的单调增函数,且当x→+∞时,φ(x)→+∞,所以不满足φ(x)max≤0.

说明在数学审题中,打开学生的思路,引导学生自觉预见解题的方向,初步确定解题的基本程序、可能用到的数学方法,强化对问题处理的理性决策意识,进而逐步提升对问题解决的整体驾驭能力．

3 在问题作答中,提升远见能力

课堂教学中停顿一定的时间,提醒学生思考,鼓励学生去体会和感悟:

说明题目的结论告诉我们向何方前进、预告“需知”,并引导解题方向．弄清了结论就等于弄清了行动的目标,也随身带上了纠正偏差的指南针．解答过程中的远见是在审题预见的基础上、在解题推进中的积极思维监控,针对出现的结果而采取的应对策略,避免了走弯路和错路,提高了解题的正确率和解题效率．

4 在解答受困时,诱发另见灵感

解题思考时会受到以往经验的迁移和影响,但面对变化了的问题,可能需要另辟蹊径,灵活应对,采取新办法才能突破困局,使问题获解．

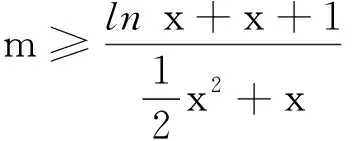
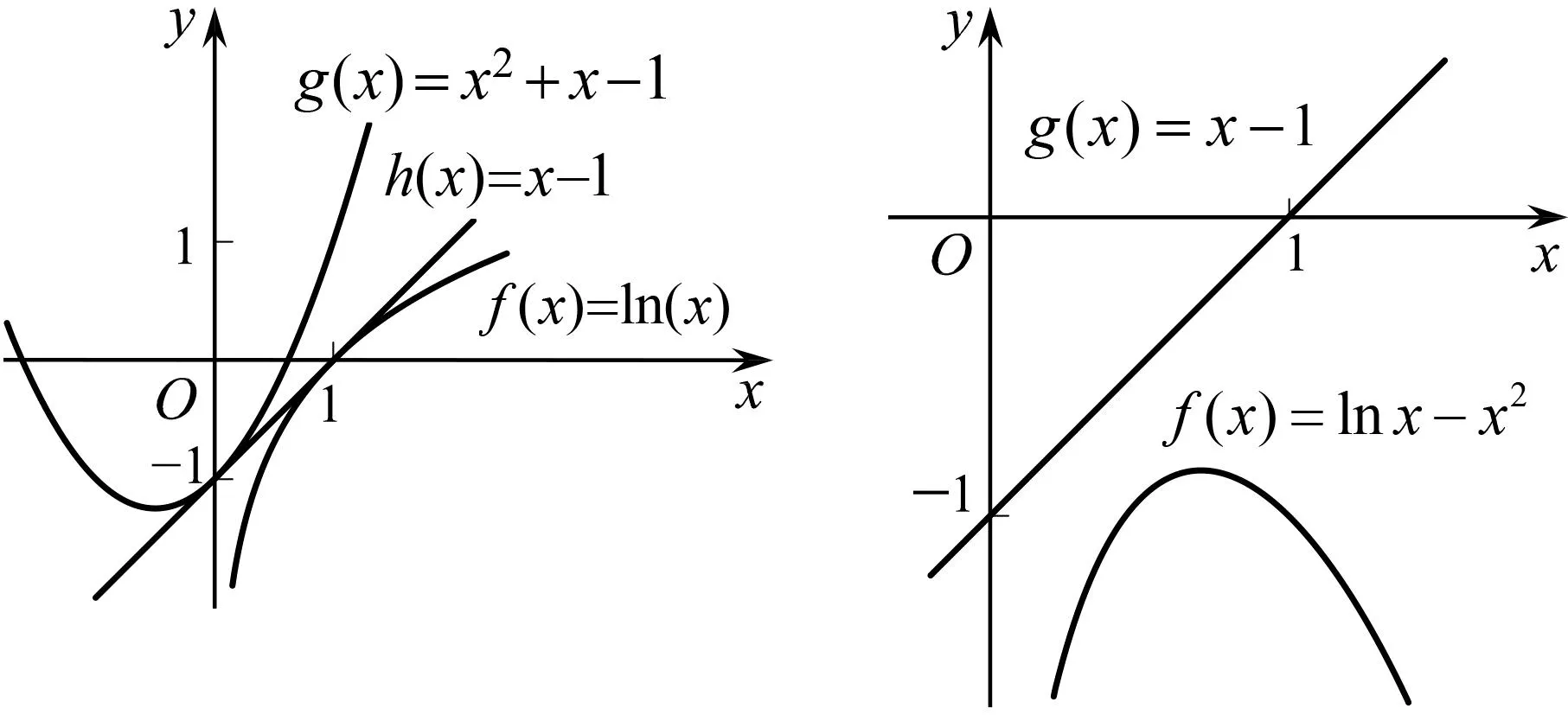
图1

如果待证不等式lnx≤x2+x-1变形为 lnx-x2≤x-1的话,则由函数图象可以直观地感受(图2)．

5 在解题完成后,养成回见习惯

历经上述问题的思考作答过程后,教师应趁热打铁,引导学生作解题回顾,体会、巩固解题成果,培养学生自觉的解题回见习惯．具体地说:回见解题方法,领会数学思想;梳理解题过程,体悟解题策略;重温难点突破,培养意志品质．

(1)回顾解题的通性通法,如题解中的参变分离、整体构造函数的带参讨论(预见2的思路方法),使学生扎实掌握相应的解题方法．

(2)对比解题方法和策略,体会面对具体受阻问题时的灵活应变．如先控制参数m的取值范围,而后猜想、确定相应的值,再进行充分性的证明,丰富解题经验,拓展解题视野,优化思维品质．

(3)感悟数学学习应该具备坚韧不拔的顽强意志,敢于发表自己的主见,发扬勇于探索的科学精神,进一步激发、强化对数学学习的兴趣和热情．

解题教学实践表明:分析典型例题的解题过程是学生学会解题的有效途径,解题教学中的例子应尽可能是范例,具有典型性、教育性,少而精,学生才能记得住,才容易领悟．解题教学是师生再发现与再创造的过程,不仅要把“题”作为研究的对象,把“解”作为研究的目标,而且要把“解题活动”作为对象,把学会“数学地思维”、促进“人的思维发展”作为目标．