基于“教学评一体化”的数学整体思维的培养——以2023年新高考Ⅱ卷第21题为例*

沈 臻

(江苏省常州市北郊高级中学 213031)

王 强

(江苏省常州市第二中学 213003)

在教育改革不断深化的背景下,“教学评一体化”越来越受到关注．教学评一体化是指在教育过程中,教学、学习和评价应相互协调,共同完成教育目标．其中,教学是手段,学习是过程,评价是反馈,三者形成一个完整的教育系统．在数学教学中,这种一体化思想对于培养学生整体思维具有重要意义．通过适切的教学行为,教师可以引导学生掌握数学知识、发展思维能力,同时利用评价手段及时获得教学反馈,不断完善教学方式．

章建跃博士指出:数学中的整体性既体现在代数、几何、三角等各部分内容之间的相互联系上,也体现在同一部分内容知识的前后逻辑关系上．“整体性”一词在课程标准中共出现16次,主要聚焦于数学课程内容、数学核心素养的培育、数学教材编写、数学教育评价等方面[1]．培根曾说“数学是思维的体操”.整体思维是指将数学知识和方法作为一个整体来理解和把握,发现其中的内在联系,形成全面的、多角度的思考方式．新高考中压轴题的突破同样需要整体思维,如函数中的同构、解析几何中的齐次化等．本文以2023年新高考Ⅱ卷第21题的根与系数关系不对称问题为例,基于教学评一体化就解析几何教学中如何培养学生的整体思维,谈一点我们的思考,恳请读者不吝赐教．

1 创建适切环境,观察整体结构

崔允漷教授基于教学评一致性设计出一个由六大要素构成的教师教学行为框架[2]．六大要素分别是:创建促进学习的环境;研究并理解学生;明晰目标与组织内容;提供多样的学习机会;促使学生学会学习;持续的教学反思与创新．良好的课堂氛围可以促进教学评一体化的实现,教师需要关注学生的情感需求和体验,营造积极和谐的课堂氛围．解析几何教学中,利用信息技术创建探究环境可以丰富教学内容和形式,帮助学生确立研究方向．

解析几何中的运算是建立在几何背景下的代数运算,所以先用几何眼光观察、分析几何图形的要素及其基本关系再用代数语言表达,在运算过程中时刻注意利用图形的几何特征及图形间的关系来简化运算,这是解析几何教学中突破运算难点的关键举措[3]．椭圆、双曲线和抛物线本身关于坐标轴对称,利用图形的整体结构(对称性),通过动态几何软件的直观呈现,可以明确运算方向．

(1)求C的方程;

(2)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于M,N两点,M在第二象限,直线MA1与NA2交于点P,证明:点P在定直线上．

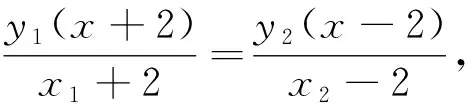
2 组织有效活动,实施整体运算

组织有效的学习活动是教师教学关键行为,包括教学目标落实、教学内容处理、教学活动实施三个方面．明确的教学目标是教学评一体化的基础,解题教学的目标不能局限于得到正确答案,还应关注方法的掌握程度(一题多解)和灵活运用(多题一解)．教学内容是培养学生数学整体思维的核心,教师应注重知识的纵横联系和拓展延伸,帮助学生建立知识的网络结构．教学活动的有效实施是实现教学评一体化的关键,教师需要积极采用启发式、探究式、合作交流等方式,引导学生主动参与到学习活动中．

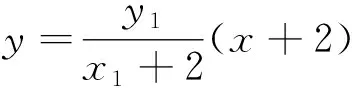
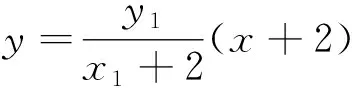
3 进行持续反思,培养整体视角

多元化评价是教学评一体化的重要环节,包括学生自评、学生互评、师评等．教师要熟练掌握各种评价方法,灵活运用在教学过程中．教学评一体化强调评价的实时性,教师要根据学生的课堂表现进行适当反馈和评价,为学生提供针对性的指导,同时反思教学过程并及时调整教学策略．教师应注重评价的育人导向功能,坚持以评促教、 以评促学,还应引导学生及时反思自己的学习过程,评估自己的学习成果,从而认识自己的优点和不足．

章建跃博士指出:“对数学对象的研究,要注重让学生经历以‘一般观念’(big idea)为引导发现规律、获得猜想,并通过数学的推理、论证证明结论(定理、性质等)的过程,提升逻辑推理、数学运算等素养．”[5]将原问题进行推广、类比、特殊化、联系是进一步研究问题的一般观念,教学中应培养学生从联系的、整体的视角看问题．可设计学生活动,对2023年新高考Ⅱ卷第21题这类定值问题进行推广,合作探究,得到其在双曲线中的一般化结论即定理1,并进一步将结论类比推广到椭圆得到定理2,推广的过程中可应用动态几何软件GeoGebra进行辅助验证．

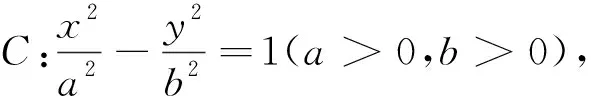
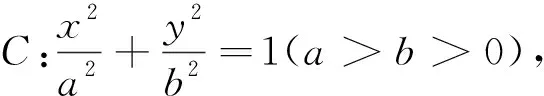
定理2的证明与定理1的证明相似,由定理2令a=b也容易推得圆中的相关结论．

用整体的眼光进一步看问题,定理1和定理2都是由定点得到定直线,那么自然思考交换条件和结论,由定直线能否得到定点呢?经过学生课后进一步探究,可得到定理3和4,证明过程不再赘述．

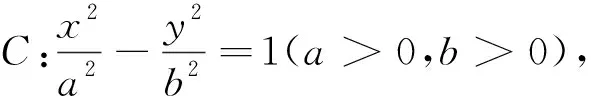
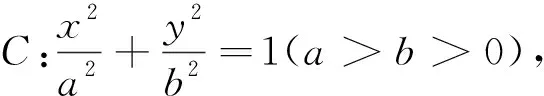
4 结束语

解析几何是运用代数运算解决几何问题,涉及到“形”与“数”的合理转化、“数”与“式”的灵活整合．在运算的设计阶段,我们需要用好图形的整体结构如充分利用圆锥曲线的对称性辅助解题,也需要结合所求问题分析式子的代数结构进行整体处理,从而明确更简便的运算方向．在运算的实施阶段,我们需要围绕代数结构和图形结构从多角度实施整体运算,感受整体运算的简便性,形成整体运算的成功体验．在运算的反思阶段,我们需要利用“推广、类比、特殊化、联系”的一般观念进一步研究问题,从解“一道题”向解“一类题”转变,提高从整体角度发现和提出问题的能力、分析和解决问题的能力．应在运算的各阶段加强整体思维的培养,从而帮助学生积累数学运算活动经验,增强数学运算的信心,提升数学运算素养．

教育的根本任务是落实立德树人,发展学生的学科核心素养．教师作为教学过程中的组织者、指导者和引领者,要确定课堂教学“教什么”“怎么教”,要指导学生“学什么”“怎么学”,最后通过评价知晓学生“会什么”的最终效果．基于教学评 一体化的数学整体思维培养是一项系统的工程,教师在教学过程中不断探索和实践．通过“创建适切环境,观察整体结构”“组织有效活动,实施整体运算”“进行持续反思,培养整体视角”等教学措施,可以有效地培养学生的数学整体思维,提升他们的数学素养和创新能力,为提高数学教学质量和培养创造型人才奠定坚实的基础．