高速铁路钢轨波磨激扰下动车组转向架振动特性
2024-03-03张茂轩周谦李连东刘金朝
张茂轩 周谦 李连东 刘金朝
1.中国铁道科学研究院集团有限公司 基础设施检测研究所, 北京 100081; 2.北京铁科英迈技术有限公司, 北京 100081
车辆高速运行时,车辆和轨道之间由于轮轨接触面的初始不平顺而产生振动,导致钢轨受力面产生不均匀磨耗和塑性变形。轨道不平顺和钢轨受力面的不均匀磨耗和塑性变形会加剧车辆-轨道系统的振动,使钢轨不均匀磨耗和塑性变形持续扩大,反复循环下,钢轨受力面波浪形磨耗逐步形成[1]。高速铁路波磨波长一般为120 ~ 150 mm,在低速区段约为60 ~80 mm。钢轨波磨是一种动态发展的钢轨表面周期性短波病害,可导致钢轨、扣件、轨下基础、轮对、构架等振动加剧[2-3],甚至会引发扣件断裂等严重后果[4]。
波长1 m 以下的短波病害往往通过轴箱加速度予以识别[5-6]。一些学者对短波不平顺幅值与轴箱加速度振动幅值的关系进行了分析,并利用轴箱加速度控制波磨等短波病害的发展[7-8]。另一些学者利用时频分析方法处理轴箱加速度数据,有效地识别轨道短波病害[9-10]。文献[11]通过轴箱加速度数据计算得到的波磨指数(Rail Corrugation Index,RCI)和能量因子(Energy Factor,EF)两个指标,识别高速铁路上波长40 ~ 300 mm 的钢轨波磨病害。文献[12]对钢轨波磨指数和能量因子的计算方法进行了改进,使之适应变速区段的计算,并能够反映钢轨波磨的幅值。
一般认为构架加速度数据较适用于处理波长8 m以上的轨道高低不平顺[13]。但考虑构架加速度计在传感器选型、后期维护等方面的优势[14],也有学者利用构架加速度进行轨道短波病害的识别。文献[15]采用SIMPACK 和ANSYS 建立刚柔耦合动力学仿真模型,模拟轨面低塌和钢轨波磨工况下的构架加速度信号,并基于时频分析方法对轨面低塌和钢轨波磨进行了识别验证。可见,利用构架加速度信号来识别波磨等钢轨短波不平顺是可行的。
本文基于实测构架垂向加速度数据,对钢轨波磨区段的数据时频特性展开研究,探索基于构架加速度信号的钢轨波磨识别方法,并通过实例进行验证。
1 测试系统及数据处理
1.1 测试系统简介
所使用数据来自于安装在一高速综合检测车的车辆动态响应检测系统。该检测系统从车下到车上分别由测试传感器、线缆、测试设备、数据处理主机、数据分析主机、显示器等组成,可测量左轴箱横向及垂向加速度,右轴箱垂向加速度,构架横向及垂向加速度,车体纵向、横向及垂向加速度,共计8 个通道,见图1。
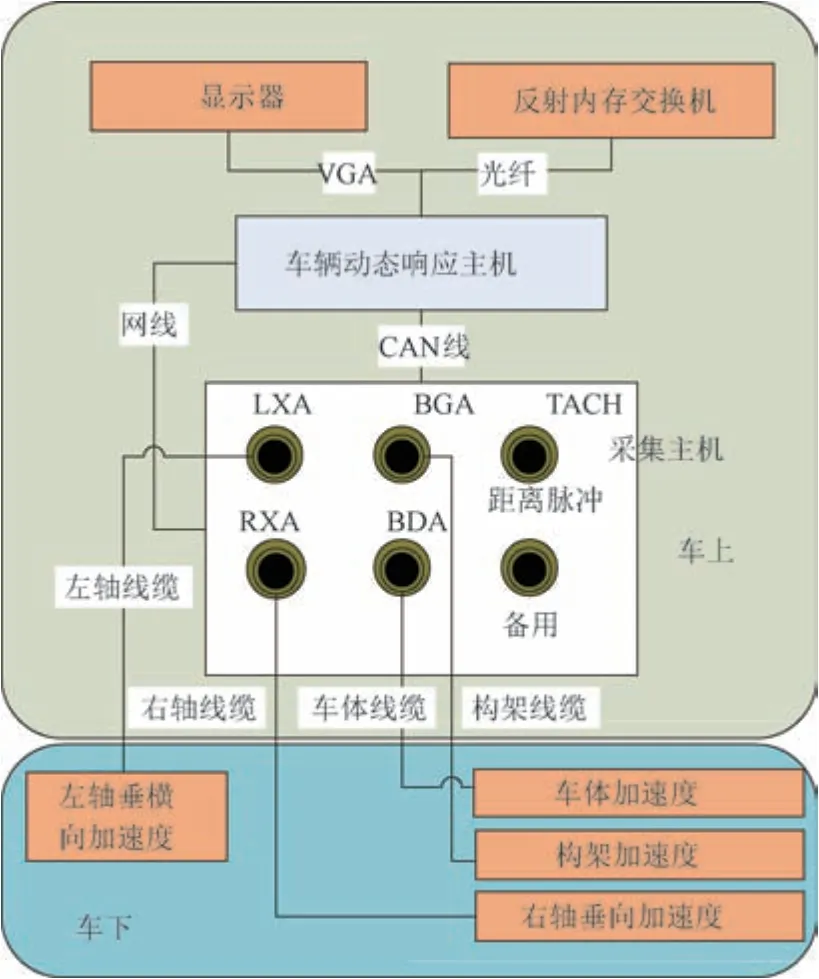
图1 车辆动态响应检测系统框架
如图2 所示,轴箱加速度计安装在被测断面的两侧轴箱上方,根据轴箱特点设计的传感器安装平台通过螺栓与轴箱连接,传感器通过4 根螺栓与平台紧密相连;构架加速度计安装在轴箱加速度计侧上方转向架构架上,同样通过特制的安装平台与构架紧密连接;车体加速度计安装在被测断面与车体纵向对称轴虚交叉点外移1 m处的车厢地板位置。

图2 加速度计安装部位
1.2 数据处理
各个通道的采样频率均为5000 Hz,涵盖了高速动车组有效的振动频率范围和钢轨波磨病害能够引起的振动频率范围。
钢轨波磨属于周期性短波病害,可引起车辆的周期性高频振动。可能引起车辆周期性高频振动的还有车轮缺陷,如车轮扁疤、擦伤、多边形等,会对车辆运行造成更大的激扰。本文不考虑车轮缺陷引起的周期性高频振动。
2 钢轨波磨区域构架振动特点
利用某型高速综合检测列车在经过不同工况区域时测试得到的垂向振动加速度,对比分析不同波磨波长以及非波磨条件下动车组垂向振动传递规律及构架垂向振动特点。
2.1 轴箱-构架-车体传递规律
2.1.1 数据处理
利用统计方法和傅里叶变换,计算波磨区域和非波磨区域动车组振动加速度幅值变化情况。采用75%分位数作为一组振动数据的大值代表,借助该指标评价列车在经过不同区段时的车辆整体振动幅值自下而上的衰减规律。对不同工况下加速度时域抽样数据进行快速傅里叶变换(Fast Fourier Transform,FFT),采用文献[16]中的功率谱能量指标,表示特定频带的加速度功率谱能量,以计算特定频带的能量占比。信号x(t)进行FFT处理后的功率谱[Pxx(eiω)]为
式中:ω为角频率;rxx(t)为信号x(t)的自相关函数;t为时间。
总均方根加速度(Grms)可表述为
式中:Re、Im分别为变换数据对应的实部、虚部;n为输入序列的长度。
2.1.2 对比分析
综合检测列车高速通过某300 km/h 速度等级无砟高速铁路线路时,轴箱-构架-车体的垂向加速度时域波形见图3。可知:列车高速通过时,波磨区段轴箱和构架加速度的幅值明显大于非波磨区段,而车体的振动信号则未表现出明显区别。

图3 轴箱-构架-车体垂向加速度时域波形
1)波磨区段
经现场复核,波磨区段的波长约为150 mm,可推算其理论振动频率为556 Hz。波磨区段轴箱-构架-车体垂向加速度箱形图见图4。可知:综合检测列车经过波磨区段时,轴箱、构架和车体垂向加速度幅值75%分位数分别为42.59g、1.64g和0.08g,由此推断总体振动衰减幅度分别为96.15%(由轴箱到构架)和95.12%(由构架到车体)。
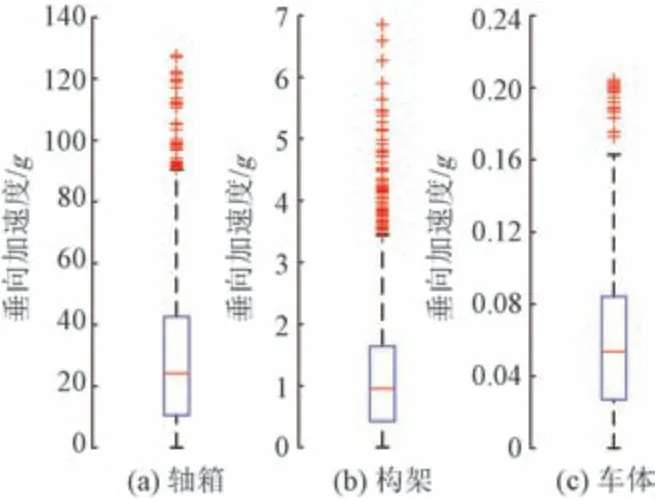
图4 波磨区段轴箱-构架-车体垂向加速度箱形图
波磨区段的轴箱-构架-车体垂向加速度频谱见图5。可知,轴箱和构架在理论波长556 Hz 范围附近存在一处明显峰值,而车体加速度频谱能量则主要集中在0 ~ 200 Hz。选取500 ~ 600 Hz 频带的总均方根加速度作为波磨引起的振动能量,该频带范围内构架的总均方根加速度为0.57g,占全频带范围内总均方根加速度的65.12%。
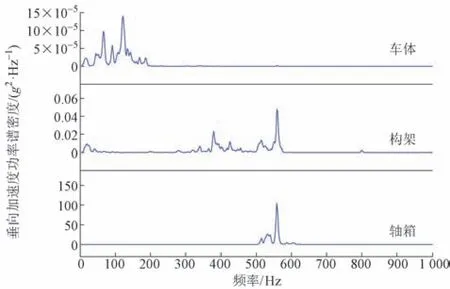
图5 波磨区段轴箱-构架-车体垂向加速度频谱
2)非波磨区段
在非波磨区段(无其他轨面短波病害),轴箱-构架-车体垂向加速度箱形图见图6。可知:综合检测列车在经过非波磨区段时,轴箱、构架和车体垂向加速度幅值75%分位数分别为5.86g、0.46g和0.07g,由此推断总体振动衰减幅度分别为92.15%(由轴箱到构架)和84.78%(由构架到车体)。

图6 非波磨区段轴箱-构架-车体垂向加速度箱形图
非波磨区段轴箱-构架-车体垂向加速度频谱见图7。可知,轴箱位置的垂向振动频率主要分布在500 ~ 700 Hz 以及20 ~ 50 Hz,构架垂向振动频率主要分布在5 ~ 50 Hz 以及340 ~ 480 Hz,车体垂向振动频率主要分布在0 ~ 200 Hz。500 ~ 600 Hz 频带内构架垂向加速度的总均方根加速度为0.0086g,占全频带范围内的总均方根加速度的4.56%。

图7 非波磨区段轴箱-构架-车体垂向加速度频谱
2.2 振动幅值与频次
选取动车组运行时速均为300 km 的波磨区段和非波磨区段轴箱、构架和车体加速度数据进行对比分析,其振动幅值见图8。

图8 轴箱-构架-车体振动幅值
由图8可知:无论是波磨区段还是非波磨区段,三个部位的振动幅值和频次均成反比。对于波磨区段,轴箱、构架和车体垂向加速度最大幅值分别为121.20g、6.50g和0.19g,从轴箱到构架最大幅值的下降幅度为1865%,从构架到车体最大幅值的下降幅度为3421%;对于非波磨区段,轴箱、构架和车体垂向加速度最大幅值分别为25.93g、3.46g以及0.25g。从轴箱到构架最大幅值的下降幅度为747%,从构架到车体最大幅值的下降幅度为1388%。由此可知,波磨区段轴箱和构架的振动能量更大,衰减更快,总体下降幅度是非波磨区段的250%。无论波磨区段还是非波磨区段,从轴箱到构架的下降幅度约为从构架到车体下降幅度的54%,表明从构架到车体的能量衰减更迅速。同时,相同运行速度下,波磨区段相比非波磨区段构架垂向加速度最大幅值增大约88%。
2.3 钢轨波磨区段构架振动时频特征
短时傅里叶变换是在信号x(t)做傅里叶变换前乘以窗函数[h(t)]。通过将窗函数在时间轴上滑动,对信号逐段进行分析,得到信号x(t)的一组局部频谱。时频分析的优点在于能够同时考虑信号在时域和频域两个方面的性能,从而更好地分析信号的特征。信号x(t)的短时傅里叶变换[F(t,f)]表达式为
式中:f为频率;τ为窗函数中心。
该波磨区段构架垂向加速度信号时频图见图9。可知:波磨区段构架垂向加速度在556、520、380 Hz 三个频率附近能量较为集中,其中520 Hz 频带只在区段前部的能量较高,区段后部则较弱。同时,考虑到波磨波长为150 mm,结合该区段运行速度,其理论振动频率约为556 Hz。因此,判断556 Hz 频段为波磨引起的特定振动频率。
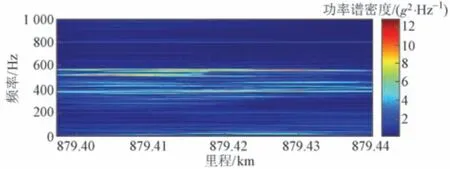
图9 波磨区段构架垂向加速度时频图
3 利用构架垂向加速度识别钢轨波磨
高速铁路钢轨波磨会导致构架加速度信号出现周期性变化,但其特征不如轴箱加速度明显,须使用特定方法进行提取。本文使用基于自适应噪声的完备总体经验模态分解(CEEMDAN)和平滑伪Wigner‑Ville 分布(SPWVD)的时频分析方法(CEEMDAN‑SPWVD),提取构架加速度信号中的波磨周期性成分。步骤如下。
1)对构架垂向加速度信号x(t)进行CEEMDAN 处理,得到14 个本征模态分量(Intrinsic Mode Functions,IMF),记为x1,x2,…,x14;
2)对IMF分量进行筛选,剔除噪声IMF分量;
3)对含有主要振动信息的IMF 分量进行二次去噪;
4)对去噪后的每一个主IMF 分量进行SPWVD处理;
5)将主IMF 分量的时频结果相加,得到原始信号的时频分布;
6)求解原始信号时频分布的时域边际谱;7)根据设定阈值进行超限判断。
3.1 CEEMDAN
CEEMDAN 是Torres 等[17]在经验模态分解(Empirical Mode Decomposition,EMD)和集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)基础上提出的一种能够有效分解出信号中局部和非线性特征的经验模态分解方法。该方法可通过自适应的方式添加噪声,更好地解决了经验模态分解中的模态混叠问题。
设Ei(*)为经EMD 处理后的第i个本征模态分量,为经CEEMDAN 处理后的第i个本征模态分量;v(j)为符合标准正态分布的白噪声,j= 1,2,…,N,N为添加白噪声次数;ε为白噪声的标准表;y(t)为待解析信号;ri(t)为残差。CEEMDAN算法步骤如下。
1)将原信号与白噪声叠加得到新信号,对新信号进行EMD处理得到一阶本征模态分量[C(j)1(t)]。计算式为
式中:q= 1、2,q= 1 表示待解析信号减去噪声信号,q= 2表示待解析信号加上噪声信号。
2)计算N个模态分量均值,得到经CEEMDAN 处理后的一阶本征模分量。计算式为
3)计算减去一阶本征模分量后的残差[r1(t)]。计算式为
4)将残差与白噪声叠加得到新信号,对其进行EMD 处理,得到模态分量[D(j)1(t)]。对N个模态分量求平均值,得到CEEMDAN 处理后的第2 个本征模态分量。计算式为
5)计算减去二阶本征模分量后的残差[r2(t)]。计算式为
6)循环执行上述步骤,直至残差信号为不可分解的单调函数。最终得到K个本征模态分量,而原始信号y(t)被分解为
3.2 SPWVD
非平稳信号时频分析方法SPWVD 可将信号y(t)进行时频分析,得到时间和频率的联合函数[p(t,f)]。其分布形式为
式中:Az(τ,ν)为模糊函数;φ(τ,ν)为核函数。
当核函数φ(τ,ν) = 1时,得到分布
由于WVD 处理后的信号存在交叉项,可通过对信号加窗处理进行消除,得到伪Wigner‑Ville 分布(PWVD),表达式为
式中:z(t)为原始信号y(t)的解析信号;h(τ)为一个矩形窗函数。
滑动窗可有效抑制交叉项,但另一方面该矩形窗也会降低频率分辨率。平滑伪Wigner‑Ville 分布(SPWVD)分别在时间域和空间域对u和τ加窗函数g(u)和h(τ),独立确定时间和尺度分辨率,几乎没有交叉项。其中,g(u)表示在时间点为u的时刻加窗函数[g(u)]。g(u) 和h(τ) 是两个实值函数,且g(0) =h(0) = 1。SPWVD表达式为
4 识别案例
利用CEEMDAN‑SPWVD 方法,分析高速铁路构架垂向加速度信号,识别钢轨波磨区段。
4.1 CEEMDAN分解
对构架垂向加速度(Bogie Acceleration,BA)信号进行CEEMDAN 处理,得到14个IMF分量。图10自上而下依次为构架垂向加速度信号经CEEMDAN 处理后的第1—第8阶IMF分量。

图10 前8阶IMF分量
4.2 SPWVD分布
对前8 阶IMF 分量进行去噪,并进行SPWVD 变换,得到各IMF 分量的时频分布结果,见图11。可知,第2—第3 阶IMF 分量在500 Hz 主频附近存在能量集中现象;第4—第8 阶IMF 分量主频在400 Hz 以下,阶数越高,其主频越低。

图11 前8阶IMF分量SPWVD分布(时频)
4.3 原始信号时频分布
为排除低频振动影响,不考虑4阶后的IMF 分量,将前3 阶IMF 分量的时频结果相加,得到原始信号的时频分布,并计算其时域边际谱和频域边际谱,见图12。可知:构架垂向加速度在该区段范围内的时域边际谱能量较高,其功率谱密度最大为12.13g2Hz-1,为正常工况(5g2Hz-1)的2倍以上,推断该区段存在波磨。通过频域边际谱可知,主频约为490 Hz,理论振动波长约为170 mm。现场复核发现,该区段存在波磨病害(图13),波长为150 mm,与理论计算频率接近。
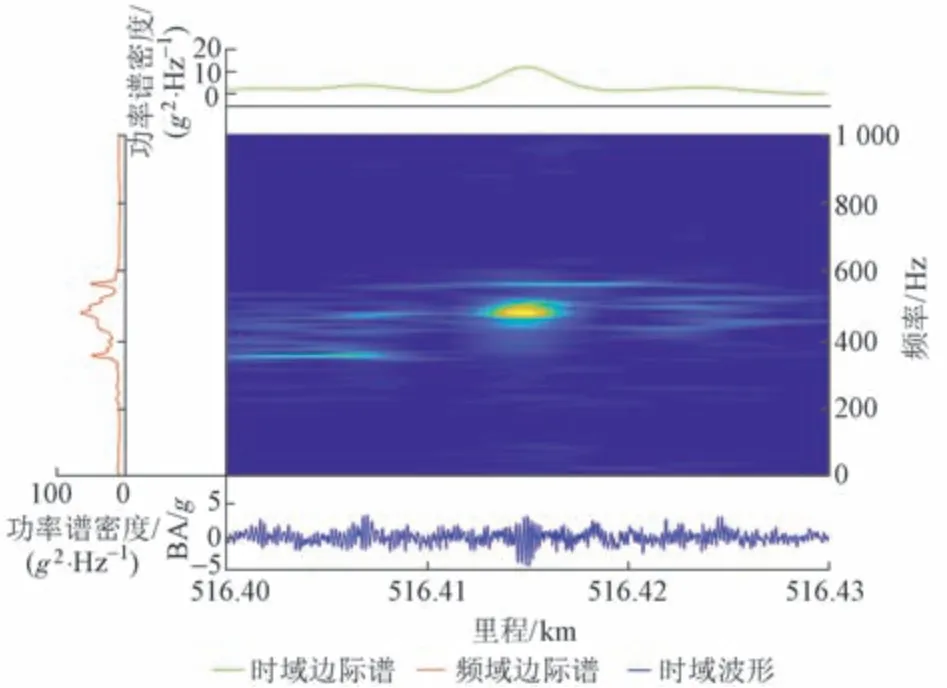
图12 构架垂向加速度时频分布

图13 现场复核图片
5 结论
1)相同运行速度下,波磨区段相比非波磨区段构架垂向加速度最大幅值增大约88%,且波磨区段500 ~ 600 Hz 频带范围内的总均方根加速度在全频带范围内的总均方根加速度占比65.12%,远大于非波磨区段的4.56%。
2)波磨区段轴箱和构架的振动能量更大,从轴箱到构架的振动能量衰减更快,加速度总体下降幅度是非波磨区段的250%。无论波磨区段还是非波磨区段,从轴箱到构架的衰减倍数约为从构架到车体衰减倍数的54%。
3)基于自适应噪声的完备总体经验模态分解(CEEMDAN)和平滑伪Wigner‑Ville 分布(SPWVD)的时频分析方法能够有效分离构架垂向加速度中的不同振动成分,便于波磨区段的构架垂向振动特征提取。
4)基于重构后的SPWVD 分布时域边际谱,能够有效识别钢轨波磨区段。经现场复核,验证了算法的有效性。
