把握数学概念本质 发展学生数据意识

作者简介：张艳华，辽宁省实验学校高级教师。

摘要：平均数是统计学中的一个重要概念，是培养学生数据意识的重要载体。对于平均数，教材的教学指向非常明确，即在具体情境中不仅要会计算一组数据的平均数，更应理解其概念本质，感悟平均数的统计意义。教学中，教师要进行学情检测，把握学习起点；分层建构，发展数据意识；运用拓展，研判平均数的价值。

关键词：平均数；概念本质；数据意识

数据意识是《义务教育数学课程标准（2022年版）》（以下通称“新课标”）中提出的学生在义务教育阶段数学课程中特别需要培养的数学基本素养之一，数据意识主要指对数据的意义和随机性的感悟。“平均数”是人教版数学教材四年级下册第八单元“统计”例1、例2的学习内容。小学数学所研究的平均数指算术平均数，就是一组数据的总和除以总份数就能够得到一组数据的平均数，反映的是一组数据的整体水平，具有代表性、区间性、虚拟性和敏感性等特性。对于平均数，教材的教学指向非常明确，即在具体情境中不仅要会计算一组数据的平均数，更应理解其概念本质，感悟平均数的统计意义，发展数据意识。

一、学情检测，把握学习起点

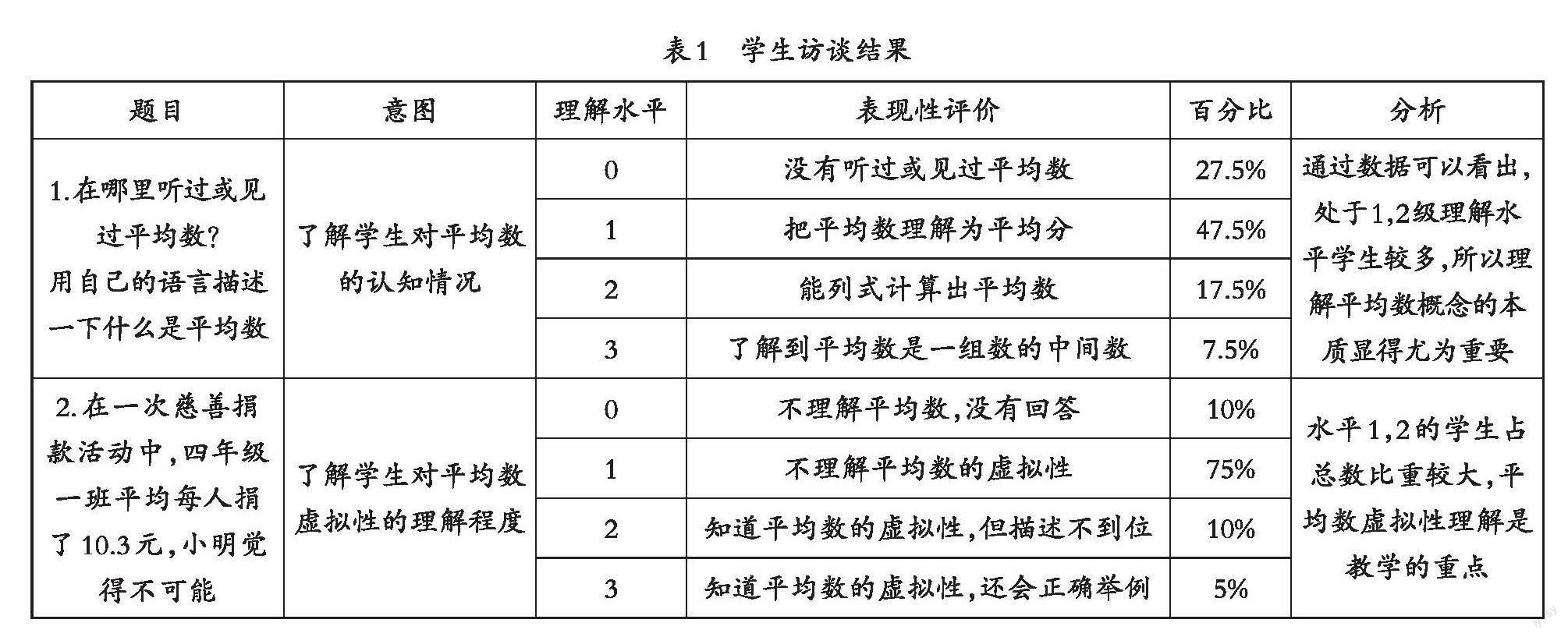
从统计的角度去理解平均数的意义，对于学生来说是有一定困难的。为了准确地把握学生的学习起点，教师对学生进行了学情检测，结果见下页表1所示。

通过表中两个题目的分层次分析我们可知，学生对于平均数的理解存在以下两个问题：一是平均数与平均分产生混淆。平均数是在学生理解了平均分和除法运算含义的基础上进行学习的，从第1，2题的解答可以看出，学生已有平均分的学习经验，但很容易把平均数与平均分等同起来；二是平均数的统计学意义理解不够。在学习平均数之前，四年级学生所认识数都是表示具体事物数量的数，具有现实性，而平均数不反映具体事物的多少，表示一组数据的总体水平，它可能等于一组数据中的某个数，也可能是一组数中不存在的，具有虚拟性。这对学生的认知来说是一个巨大的挑战。从第2题的解答可

以看出学生对平均数统计学意义的理解较为欠缺，需要借助合适的现实情境感悟。

二、分层建构，形成数据意识

基于以上分析，本课的教学应着重解决以下3个问题：一是通过创设贴近生活、生动有趣、指向数学概念本质的学习材料（以下简称“学材”），使学生感受平均数产生的必要性，会用移多补少、求和均分计算一组数据的平均数；二是引导学生经历观察、思考、计算、交流等一系列活动，理解平均数是代表一组数据整体（平均）水平的量值，体验平均数的虚拟性、敏感性、区间性；三是应该通过多维的变式练习使学生能用平均数解决简单的实际问题。

（一）优化学材，初步体会平均数的意义

“对数据的需要”是学生形成数据意识的起点，它要求学生在具体情境中认识到数据分析有助于问题解决，进而产生引进新的统计量的需求。在教学时，教师应准确把握学生这一起点，优化学材，引导学生主动参与学习活动。

师：看到“平均”两个字，你想到了什么？

生：我想到了分桃子，把10个桃子平均分给5个人，每人分到2个。

生：我想到了把一块蛋糕平均分成8块，我家4人，每人分得2块。

生：我想到了每人分得同样多。

师：那么，看到“平均数”三个字你又想知道些什么呢？

生：我想知道什么是平均数。平均數与平均分有什么关系？平均数怎么求？学习平均数有什么用？

师：提出问题比解决问题更重要。会提问题，说明你们会学习、会思考。

教师出示改编的例1：东东同学是学校环保小队的成员，四天来，他每天收集饮料瓶的数量分别是12，14，15，11个，请问他平均每天收集多少个饮料瓶？

【设计意图】通过回忆平均分激活学生已有经验，同时通过提问引发学生产生对于平均数的新思考。

（二）探究新知，分层建构平均数的计算方法

平均数的统计学意义（代表性、区间性、虚拟性、敏感性等）对于刚入四年级的学生来说很难理解，教学中除了引导他们掌握平均数的计算方法，教师更应重视通过多重辨析，使其经历观察、猜想、计算的过程，深入感知、感悟平均数的特征。

1. 看图理解含义，探求方法

教师出示任务：东东犯难了，请你帮他在任务单中写出建议的数据。

生：我填的是15，因为最多的是15。

生：我填的是14，因为最多的是15，最少的是11，如果这四天每天同样多，不可能比最多的多，也不可能比最少的少。

师：谁读懂他的意思了？

生：他的意思是平均数要比最多的少，比最少的多。

师：可能是16吗？可能是10吗？平均数在11到15之间，而这两个数之间有12，13，14，到底是哪个呢？怎么让别人一眼就能看出平均数是多少呢？

生：可以移动珠子。

师：你怎么想到移动珠子了呢？

生：我看到黑板上有珠子，而且珠子的高度不同，这样通过移动就能够让它们同样高，也就能看出平均数是多少了。

生：把14移动一个到12的上面，把15移动两个到11的上面，这样这四个数就都变成13了。也就是相当于每天都是13，达到了每天同样多。

师：这13个是第一天收集的饮料瓶数吗？

教师小结：像这样一组数据中，通过“移多补少”方法，得到相同的数13，13就是这几个数的平均数。

2. 思考辨析，感悟虚拟性

教师提出问题：“平均数‘13’是具体的数吗？你是怎么理解平均数（平均数介于最大数与最小数之间，反映的是这几个数平均后都相等而得到的数，可以等于其中的某个具体数，也可以不等于其中的任意一个数）13的？“观察四天的平均数与每天收集饮料瓶的数量，平均数代表的是整体水平，并不是这组数据中某个具体的数。

3. 举例估算，感悟敏感性

如果第五天东东收集了100个饮料瓶，平均数还会是13吗？会发生怎样的变化？

生：平均数不会是13，我认为大约是30多个，因为100相对于前几天的数据太大了。

生：我们也同意。

师：无论怎么样，会超过100吗？

生：不会，会介于11和100之间。

师：如果第五天只收集到2个饮料瓶呢？平均数会发生怎么样的变化？

生：会比13小。

生：会在2和15之间。

师：由此你们有什么发现？

生：平均数很敏感，每个数据的变化都会对它产生影响。

师：这位同学用到了“敏感”一词，事实上，每个数据的变化都会带来平均数的改变。

教师小结：通过刚才的探究我们发现，平均数很奇特，它不是具体每一天收集饮料瓶的数量，但却能反映出这四天的整体情况。而且我们发现，平均数介于最小数和最大数之间；同时，平均数又很敏感，任何一个数据的变化都能够引起平均数的改变。

4.丰富算法，理解运算本质

教师提出问题：有时候我们可以用“移多补少”方法计算平均数，但是也有些数据比如身高、体重或者较大的数据等不方便用“移多补少”方法，我们还有别的方法吗？

学生组间交流汇报：先把四天的数量加在一起，然后除以4。

师：有多少位同学是按照这种方法计算的？我们给这种方法起个名字可好？

生：先加后除法，先总后分法，先和后均法。

师：同学们真有智慧，为了方便交流，像这样先求总数再求平均数的方法，叫“先总后分”法，即平均数 = 总数量 ÷ 总份数。

【设计意图】教师注重使学生自主探索、合作交流，通过解决“东东平均每天收集多少个饮料瓶”的问题，引导学生思考并理解平均数的意义，掌握“移多补少”以及“先求和再平均分”的数学方法。

教师小结： 刚才我们通过“移多补少”和“先总后分”的方法，都求出了东东每天收集饮料瓶的平均数。我们来看，这个平均数13并不是每天真正收集的饮料瓶数量，而是一个“虚拟”的数，它反映了这几天平均每天收集饮料瓶数的一般情况。

（三）估算平均数，理解使用平均数的必要性

教师提出过渡问题：下面是第4小组男生队和女生队踢毽比赛的成绩。你认为哪个队成绩好（见图1）？

先交流：怎样判断两队中哪一队的成绩好？判断成绩好，能不能用总数来判断？为什么？用什么来判断更好呢？再猜测一下，哪个队的成绩会更好？然后，通过计算的方法验证谁猜测得更准确。

教师小结：当我们遇到“两个小组人数不等，踢毽数量也不等”的问题时，再比较总个数就不公平。这时，我们需要使用一个新的数来表示每组学生踢毽的整体水平，这个数就是平均数。

三、运用拓展，巩固数据意识

平均数在生活中运用非常广泛，教师要引导学生通过解决简单的实际问题，对数据信息进行后续推断、预测，提高对平均数概念的认知，感受平均数的合理性与独有价值，同时也认识到平均数的局限性，巩固数据意识。

（一）身边的平均数

教师提出问题：找班上的3名同学，了解、纪录其身高和体重情况。

（1）这3名同学的平均身高、平均体重各是多少？

（2）张俊才是现今中国最高的人，身高达到2.42米，如果这3名同学加上张俊才，4人的平均身高是多少？

【设计意图】调查计算班上3名同学的平均身高和平均体重，指向数据收集和计算平均数。第二小题中求4人的平均身高，可以使学生感受到极端数据会对平均数产生较大影响。

（二）生活中的平均数

教师提出问题：2022年，辽宁省平均每户3.25人。2022年，某地教师的人均预期寿命为79岁。

独立思考并交流：为什么有0.25个人？每户不到4人，你有什么想说的？已退休多年的李老师今年78岁，看到这则新闻很焦虑，你猜猜他是怎么想的？你会如何解释呢？

【设计意图】计算人的个数时应取整数，这里出现了0.25个人，也就是说平均数并不一定是现实中具体的某个数。消除李老师的焦虑可以从平均数的区间性来解释，在这个过程中可以使学生进一步感受平均数的意义和价值。

（三）比赛中的平均数

教师提出问题：读书节朗诵比赛中邀请了5名家长作评委，表2中是四年级一班的成绩，请你先去掉最高分和最低分，然后算一算，四年级一班在这次比赛中的平均分是多少？

【设计意图】在生活中常见的比赛计分情境中，通过去掉最高分和最低分，可降低极端数据对平均数的影响，增强学生解决问题的能力，提高应用意识。

（四）平均数的局限性

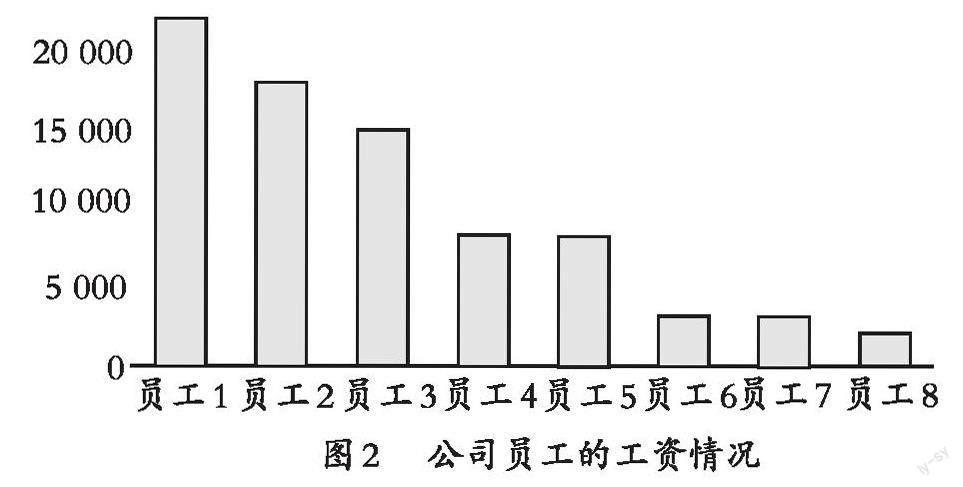
图2统计的是一个公司员工的工资情况，你能用手势比画一下这个公司员工的平均工资吗？这里的平均工资水平能反应每位员工的真实工资情况吗？

【设计意图】新课标在对数据意识的描述中提到：“感受到对于同样的一组数据可以有多种分析的方法，需要根据背景和需要，选择恰当的方法。”学生意识到现实生活中并不是每次数据的统计分析都适合用平均数来表示，其有局限性，也为后续的学习做出铺垫，巩固了数据意识。

通过“平均数”一课的教学，教师要引导学生把握概念本质，分层建构概念，發展数据意识，从而达成以生为本的课堂样态。

参考文献：

［1］牛献礼.从统计学的角度理解平均数［J］.小学教学研究，2017（4）.

［2］刘加霞.“平均数”的本质及小学生理解水平解析［J］.湖北教育（教育教学），2021（2）.

（责任编辑：杨强）