基于k-体分划的D-concurrence多体纠缠测度

崔世杰,黄 丽,王银珠,马瑞芬

(太原科技大学 应用科学学院,太原 030024)

量子纠缠被认为是量子系统之间的非经典相关性,已经引起了研究者越来越多的关注。量子纠缠的目的最初来自量子通信[1-2]。近年来,纠缠被认为是量子信息论的一种资源,并广泛应用于量子通信和信息处理中[3-5]。将量子纠缠作为一种资源的使用不仅涉及到如何检测量子纠缠的问题,同时还涉及到如何量化量子纠缠,为此人们耗费了大量的时间和精力去研究纠缠的检测和度量。经过几十年的发展,已经取得了大量成熟的理论结果。在判别量子态是否纠缠方面有著名的部分转置判据(PPT判据)[6],重排判据(RCCN判据)[7-9],约化判据[10]等。自从1997年Vedral[11]提出纠缠测度的概念后,在纠缠测度方面有了丰富的成果,Concurrence纠缠测度[12-15],形成纠缠度(EoF)[16-19]以及负性纠缠度(Negativity)[20].目前基于不同的角度定义了多种纠缠度量,然而其中大部分很难计算出来,或仅限于应用,所以寻找新的便于计算的纠缠测度是现在亟需研究的问题。

Ma.[22]等人引入了一种新的纠缠测度,称作D-concurrence.设H=HA⊗HB,对于H中的纯态|ψ〉而言,D-concurrence的定义为:

其中det为矩阵的行列式函数。

对于混合态ρ∈S(H)而言,D-concurrence的定义是通过凸顶(Convex-roof)结构定义的

其中最小值是取遍ρ的所有可能的系综分解(在这里,{Pj(|ψj〉)}称为ρ的系综分解,ρ=∑Pj(|ψj〉)(|ψj〉),以{Pj}为概率分布,{(|ψj〉)}为一族纯态)。

1 基本定义与主要结果

定义2(k-可分) 设存在一个k-体分划:

使得n体量子系统H中的一个纯态可以写成:

|ψ〉=|ψ1〉A2…|ψk〉Ak

则称|ψ〉为一k-可分态。其中|ψi〉Ak分别为对应子系统Ai中的量子态。

ρ=|ψi〉|ψi〉=

(*)

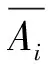
下面给出基于k-体分划的D-concurrence的定义.

其中下确界取遍ρ的所有可能的纯态分解。

下面证明k-ME D-concurrence多体纠缠测度是定义良好的。

Dk-ME(ρ)

证明:因为在局部酉算子的作用下不改变对应子系统上约化密度算子的特征值,从而在局部酉操作det(I-ρAi)不会改变,故Dk-ME(ρ)=0在局部酉操作下不改变。

Dk-ME(tρ+(1-t)σ)≤

tDk-ME(ρ)+(1-t)Dk-ME(σ)

下面证明k-ME D-concurrence在LOCC下的单调性,为此需要以下引理。

引理[24]设ρ∈S(H),H=HA⊗HB,dimH<+∞,设Λ为LOCC操作,则:

D(Λ(ρ))≤D(ρ)

Dk-ME(Λ(ρ))≤Dk-ME(ρ)

Di(Λ(ρ))≤Di(ρ)

从而:

2 结语