非绝对型Henstock 积分与Riemann－Stieltjes 积分之关系

李 伟

( 集美大学 理学院，福建 厦门361021)

继Riemann 积分［1］(简称R－积分)之后，1902 年在测度论［2］的基础上建立了Lebesgue 积分［3］(简称L－积分)，它推广了R－积分但不是R－积分的全部推广，比如广义R－可积不一定是L－可积，从空间完备化观点看，L－积分不过是C［a，b］(连续函数类)中函数R－积分的一种完备化扩张［4］．可见L－积分具有一定的局限性．因此，人们一直试图寻找一种新的积分．直到1957－1958 年，J．kurzweil 和R．Henstock 分别独立建立了一种完全Riemann 型的积分，称为Kurzweil－Henstock 积分［5］(简称KH－积分，也简称H－积分)．H－积分的本质是“非绝对型”的，因此，有时也称之为非绝对型积分．它既推广了L－积分，又包括了Newton 积分［6］和反常R－积分．此外，与有界变差函数类联系起来的有一类Riemann－Stieltjes 积分［3］(简称RS－积分)与H－积分又有什么关系呢?本文就H－积分与RS－积分之间的关系进行研究．首先给出δ(x)精细分划［7］的定义，然后引进区间［a，b］上的H－积分．利用Henstock 引理，给出Henstock 积分与Riemann－Stieltjes 积分之间的关系定理，并给予简捷证明．由此得到一推论，即定理3．

1 预备知识

定义1［7］设δ(x)为区间［a，b］上的正值函数，对区间［a，b］任作分划:

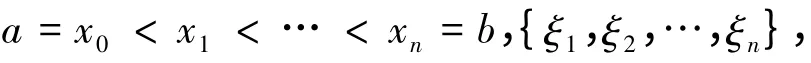
满足:ξi－δ(ξi)＜xi－1≤ξi≤xi＜ξi+δ(ξi)，i=1，2，…，n;即ξi∈［xi－1，xi］⊂(ξi－δ(ξi)，ξi+δ(ξi))，i=1，2，…，n．该分划D称之为δ(x)精细分划［6］．

定义2［5］实函数f(x)称为在区间［a，b］上Henstock 可积的，其积分值为A，如果∀ε＞0，∃实函数δ(x)＞0，对区间［a，b］上任作δ(x)精细分划D:

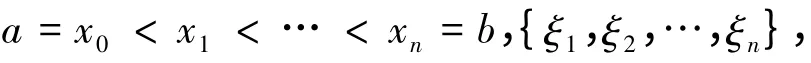
其中［u，v］为分划D中典型区间，满足:ξ－δ(ξ)＜u≤ξ≤v＜ξ+δ(ξ)，

则称f(x)在［a，b］上Henstock 可积［4］，记其积分为

定义3［8］设f(x)是［a，b］上的有限函数，在［a，b］上任取一组分点:

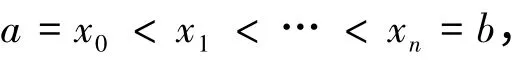
称之为f(x)对分点组x0，x1，…，xn的变差．

如果存在常数M，使，则称f(x)在［a，b］上的有界变差函数，并记:

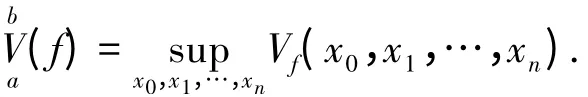
区间［a，b］上的有界变差函数全体记为V［a，b］，f(x)为［a，b］上有界变差函数，简记为f(x)∈V［a，b］．

定义4［9］设f(x)、g(x)为［a，b］上两有限函数，在［a，b］任作分划:

具有有限极限I，即:

则称f(x)关于g(x)在［a，b］上是Riemann－Stieltjes 可积的［3］(简称RS－可积)，而RS－积分值为I，记为:

特别的，当g(x)≡x时，RS－积分就是R－积分了．

2 定理及其推广

引理1(Henstock 引理)［10］若f(x)在［a，b］上Henstock 可积，且有原函数F(x)，即:

则∀ε＞0，∃δ(x)＞0，使得对［a，b］上的任何δ(x)精细子分划，即:

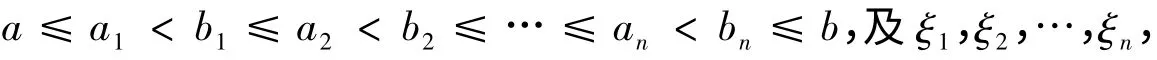
且ξi∈［ai，bi］⊂(ξi－δ(ξi)，ξi+δ(ξi))．(注意:所谓精细子分划是不要求［a，b］=∪［ai，bi］的精细分划)有:

证明 由于f(x)在［a，b］上(H)可积，故∀ε＞0，在［a，b］上有δ(x)＞0，凡δ(x)精细分划所对应的积分和，有:

［ai，bi］与ξi已经是δ(x)的精细子分划．再考虑以外的分划．

这样，每个Ji上的δi(x)精细分划，与ai，bi;ξi(i=1，2，…，n)构成［a，b］上的δ(x)精细分划．从而:

定理2 设函数g(x)在［a，b］上为有界变差函数，即g(x)∈V［a，b］，而F(x)为［a，b］上Henstock 可积函数f(x)的原函数，则:

证明 因为g(x)∈V［a，b］，又可知F在［［a，b］上连续，故右边积分存在．由RS积分定义，∀ε＞0，∃η＞0，当ξ∈［u，v］⊂(ξ－η，ξ+η)时，有:

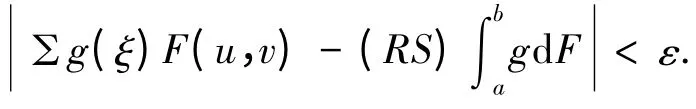
又因为f是H可积的，故∃δ(ξ)＞0，对所有的δ－精细分划，有:

由Henstock 引理，从而:

取0＜δ(ξ)≤min{δ(ξ)，η}，则对所有的δ－精细分划，有:

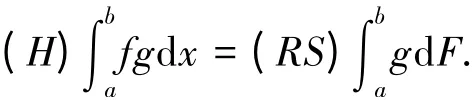
证毕．

由此可得下述分部积分公式．

定理3 若F(x)是f(x)在［a，b］上的H－原函数，g(x)是［a，b］上有界变差函数(即g(x)∈V［a，b］)，则:

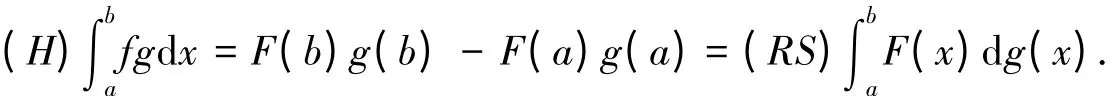
［1］ 华东师范大学数学系．数学分析［M］．4 版．北京:高等教育出版社，2010:201－203．

［2］ Donald L Cohn． Measure Theory［M］．The world book publishing company，2012:75－78．

［3］ 江泽坚，吴智泉．实变函数论［M］．3 版．北京:高等教育出版社，2010:59－75．

［4］ 李忠宁．关于R 可积函数空间的完备化［J］．河西学院学报，2010，26(5);14－18．

［5］ Henstock R．Lectures on the theory integration［M］．Singapore:World Scientific，1988:15－16．

［6］ 同济大学数学系．高等数学［M］．6 版．北京:高等教育出版社，2012:239－240．

［7］ 丁传松，李秉彝．广义黎曼积分［M］．北京:科学出版社，1989:5－8．

［8］ 包淑华．基于有界变差函数的研究［J］．廊坊师范学院学报:自然科学版，2011，11(2);16－18．

［9］ 王晟．Riemann－Stieltjes 可积的充要条件［M］．北京师范大学学报:自然科学版，2011，47(2):126－128．

［10］ Lee Peng Yee．Lanzhou Lectures on Henstock Integration［M］．Singapore:World Scientific，1989:15－28．