超高层建筑施工期结构静动态变形监测

高 珂 邓德员 朱宏平, 3 翁 顺, 3 高 飞, 3

超高层建筑施工期结构静动态变形监测

高 珂1邓德员2朱宏平1, 3翁 顺1, 3高 飞1, 3

(1. 华中科技大学土木与水利工程学院，武汉 430074；2. 中建钢构广东有限公司，广东惠州 516259；3. 控制结构湖北省重点实验室，武汉 430074)

针对超高层建筑施工期静动态变形实测研究不足的问题，在一座335 m的超高层建筑主体结构上搭建了施工期结构健康监测系统，进行主体结构施工期竖向变形、温度变形和动态位移的实测分析。探明了施工期主体结构的温度不均匀分布规律，分析了温度影响下的结构应变特点，结果表明：季节性温差引起的应变大于同时段内上部结构自重和混凝土收缩徐变引起的应变。阐释了主体结构施工期竖向变形与层间竖向变形差发展规律，层间不均匀竖向变形程度随高度和时间逐渐增大，同一层不同测点间的竖向变形差最大为5.3 mm。主梁轴向应力与其两端竖向构件的竖向应变差成正相关，外框–核心筒竖向变形差可能使主梁存在受拉开裂风险。提出一种基于卡尔曼滤波的结构动态位移估计方法，通过融合加速度数据与应变数据提高动态位移估计精度，能够准确估计超高层建筑在施工动荷载下的动态位移。

超高层建筑；结构健康监测；温度变形；竖向变形；动态位移估计

0 引 言

近十年我国超高层建筑的建造飞速发展，在各地兴建了大批超高层建筑[1]。超高层建筑变形同时受到外部和内部多种因素耦合影响，外部作用包括施工荷载、环境温湿度变化、强风及地震荷载等，内部作用包括结构自重、混凝土收缩徐变、各构件间的复杂边界约束、应力不均匀分布等。超高层建筑结构变形监测的现有研究主要集中在竖向变形、温度变形和振动位移三个方面[2]。

超高层建筑在施工阶段的结构体系、材料性能、荷载和边界条件都随时间变化，结构实际状态可能偏离设计值，结构内外竖向变形差会对主梁和楼板等横向构件产生拉应力或剪应力[3]。因此，竖向变形（差）是施工期结构健康监测的重点。Glisic等[4]采用长径光纤应变计跟踪和评估了一座高层建筑结构从施工到服役期10年间的结构的长期竖向变形。Choi等[5]监测一座72层高层建筑施工期不均匀竖向变形，给出不同构件的施工找平修正量。现有研究多集中于超高层基础沉降监测或竖向变形的有限元模拟和简化计算，缺少超高层建筑施工期竖向变形实测数据分析。

结构在日照作用下存在不均匀温度分布，产生不均匀变形。现有国家规范对结构温度做了均匀分布的简化假设，未考虑温度不均匀分布的影响[6]。Su等[7]的研究表明广州塔服役期在不均匀日照作用下一天中主塔顶部最大水平位移达16 cm，一年中因不均匀温度分布产生的最大水平位移超过30 cm，并研究了不同高度和方位的温度不均匀分布。施工期结构直接暴露于外界环境，没有保温层或幕墙隔离，更易产生不均匀温度变形。上述研究主要是超高层建筑服役期的温度变形监测，目前关于超高层施工期温度变形的实测研究仍不足。

强风和地震等动力荷载会使结构产生不同程度的振动位移，振动位移过大会导致结构不稳定甚至发生破坏。Pirner等[8]长期监测已服役30年的198 m天线塔的风致动态位移，用于评估结构性能和预测结构使用寿命。Breuer等[9]采用GPS测量已服役50年的电视塔顶部风致动态位移，并基于位移识别结构振动频率，评估结构是否存在性能退化。由于实际超高层工程体量大、设备使用受限、信号干扰等原因，难以通过常用的GPS、激光测距、机器视觉等方法直接且准确地测量动态位移[10-12]，间接测量其他相关物理量（应变、加速度等）再转换为位移的方式又存在较大的转换误差[13-14]。目前对施工期的超高层建筑的动态位移监测的研究还存在不足。

综上所述，超高层建筑施工期结构变形监测是超高层施工期安全诊断和评估的重要，目前还面临温度变形实测研究不足、动态位移测量不准确等问题。本文在一座实际超高层建筑上设计并安装了一套施工期结构健康监测系统，获取主体结构施工期的应变、温度、加速度、竖向变形等多种实测数据。基于实际监测数据，研究施工期结构温度不均匀分布特性和温度影响下结构竖向构件应变发展规律，分析结构施工期竖向变形规律，建立基于结构动态应变和加速度的结构动态位移估计方法。

1 长航大楼健康监测系统

武汉长江航运中心大楼（简称长航大楼）为框架–核心筒结构体系，建筑高度335 m。外框架为钢管混凝土柱和型钢混凝土柱组合框架，尺寸为50 m×50 m；核心筒为钢筋混凝土剪力墙，尺寸为30 m×30 m，外框和核心筒之间由钢筋混凝土主梁和楼板连接。长航大楼采用核心筒和外框架同步浇筑的施工方式，主体结构施工时间为2016年10月开始至2019年6月封顶。长航大楼截面形式较为规则，是中国中部地区框架–核心筒体系的超高层建筑结构健康监测的典型案例[15]。图1展示了主体结构在不同施工阶段的结构外形。

图1 超高层建筑的不同施工阶段

1.1 监测系统概况

长航大楼结构健康监测系统的目的包括三个方面：一是跟踪监测主体结构施工期的结构竖向变形，二是研究施工期的结构应力、应变分布情况和发展规律，三是监测施工期结构异常的发生。

该系统由4个子系统组成：传感器子系统、数据采集及传输子系统、数据管理子系统和结构状态评估子系统。其中，传感器子系统安装在主体结构的各类构件上，负责收集结构响应数据。选择6个楼层作为结构应变的监测层，传感器及采集系统布局、每个监测层的传感器测点布置如图2所示。每个监测层安装32个振弦应变计（内含温度传感元件），图中E、S、W、N分别表示东、南、西、北方向，编号1～5表示外框柱测点，6表示核心筒测点，I和II表示主梁测点。

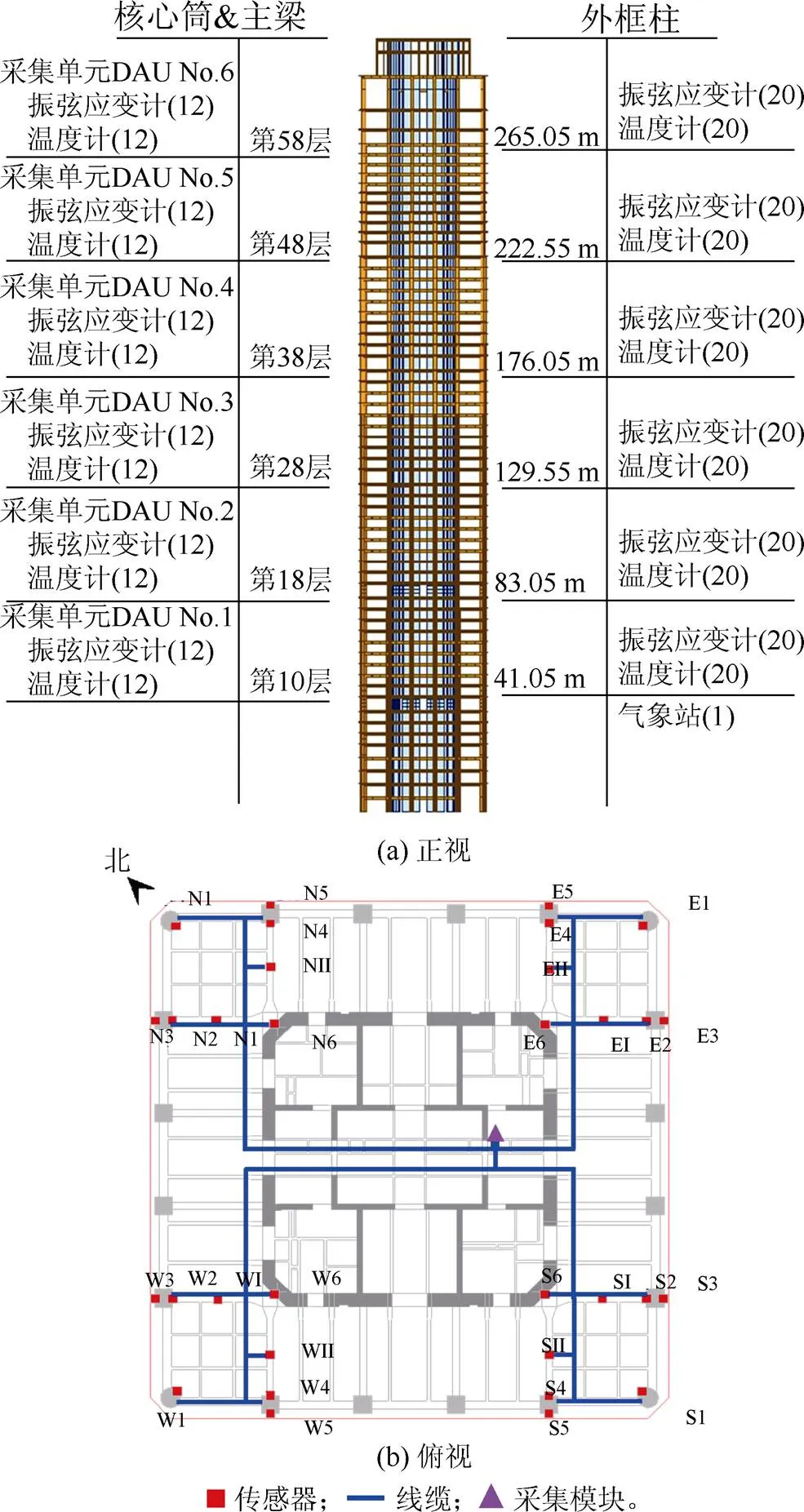
图2（a）中括号内数字为传感器的数量。

图2 传感器及采集系统布局

Fig.2 Arrangements of sensors and acquisition system

数据采集及传输子系统中包含6套分布在结构不同楼层数据采集单元（DAU）和数据传输单元（DTU），其中数据采集单元与周围传感器之间用线缆连接，负责采集监测楼层布设的传感器数据，数据传输单元则负责将采集仪所采集的信号通过无线通讯模块以无线网络的形式传到云服务器。每一套数据采集和传输单元之间相互独立，这种方式有效解决了大型结构传感器布置分散导致的集中采集困难的问题。

1.2 传感器说明

应变传感器采用BGK-4200型振弦式应变计，应变量程为±750×10–6，精度为1×10–6；其所含温度元件量程为–40～120 ℃，精度为0.1 ℃。在主体结构施工期，在被测构件（柱/墙/梁）上选取合适位置安装应变计，将传感器绑在柱/墙的中间高度处的钢筋上并保持两端自由，使得浇筑后的混凝土与传感器能紧密结合协同变形。应变传感器用于测量外框柱和核心筒剪力墙的竖向应变，以及主梁的轴向应变。

如图3所示，加速度计采用美国BDI公司的微机械电容式加速度传感器，可测量带宽范围为0～400 Hz，量程为±50 g，灵敏度为1 000 mv/g，工作温度范围为–55～125 ℃，防护等级超过IP67。加速度传感器安装在结构表面，测量结构的水平加速度。动态应变计采用美国BDI公司的电阻式应变计，量程为±2000×10–6，灵敏度为500×10–6/mV，有效标距为76.2 mm，工作温度范围为–55～80 ℃，防护等级超过IP67。这两种传感器可通过无线采集模块进行数据采集和传输，采集模块通过局域网技术将数据传至无线网关，然后通过无线网传至控制终端。

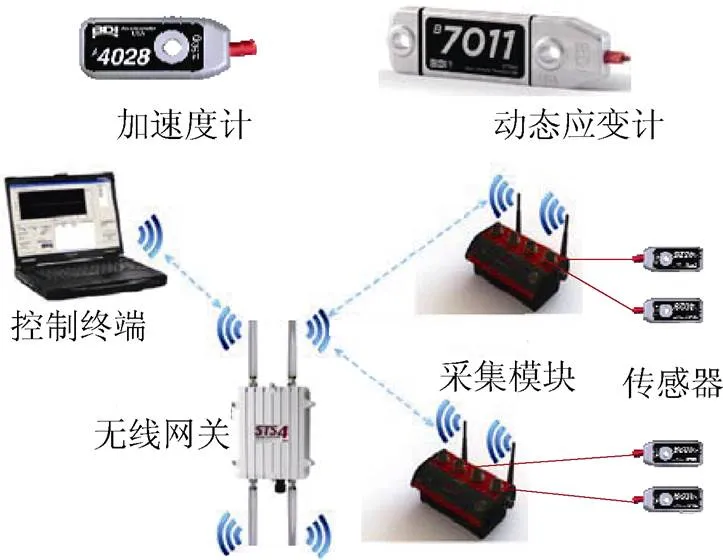
图3 动态响应监测系统

2 施工期结构温度变形监测

目前关于温度对超高层建筑施工期变形影响的研究主要依据数值模拟，实测分析不足[16]。因此，本研究基于实际监测数据分析超高层施工期温度变形规律。

2.1 施工期结构温度变化规律

主体结构第10和18层的监测分别开始于2017年7月和2017年9月。图4显示了这两层的南区测点S1从2017年7月—2018年8月期间的温度监测数据，采样间隔10 min。这两个监测楼层先经历了夏—冬的季节性降温，然后经历了冬—夏的季节性升温。环境温度变化范围−8～39 ℃，南区S1测点温度变化范围为−3～38 ℃。图5显示了第28层施工后2018年3月—2019年4月期间的温度变化。与第10层和第18层不同，第28层施工完成后先经历春—夏的季节性升温，再经历夏—冬的季节性降温。

结构不同区域受不均匀太阳辐射，结构存在温度不均匀分布的特点。以北区测点N1为基准，得S1、E1、W1测点相对于N1的温差，如图6所示。图6中温差在2017年10月—2018年5月期间基本为正值，即这期间北区温度低于其他区域；而在2018年6月—9月期间温差常为负值，说明这期间北区温度时常高于其他区域。南、北区之间平均温差最大，为9 ℃左右。另外，图中不同区域之间温差冬季最大，夏季最小。

图4 第10和18层施工期温度变化

图5 第28层测点施工期温度变化

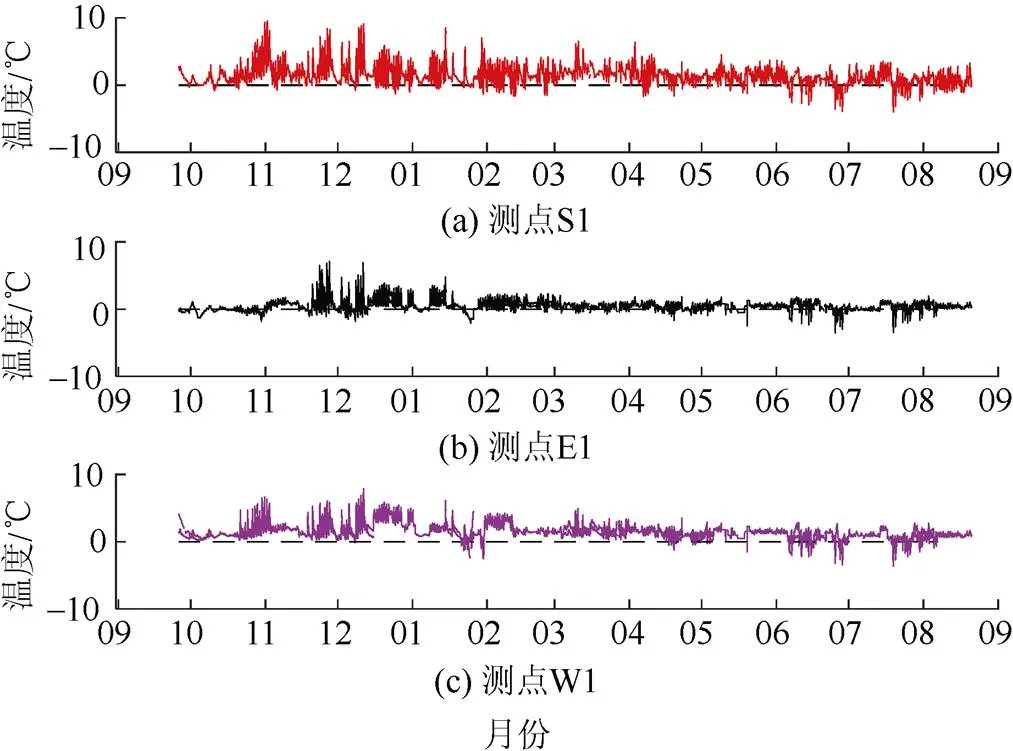
图6 各区域之间温度差异（第18层）

2.2 结构温度对应变的影响

以测点所在楼层混凝土浇筑后14天作为初始时间点，所测应变是弹性压缩、混凝土收缩徐变、温度变形这3种主要因素共同作用下的总应变。拉应变为正，压应变为负。

图7显示了第18层四根外框角柱施工后一年内的应变–时程曲线，分为两个阶段：2017年9月—2018年2月的下降段和2018年2月—2018年7月的上升段。下降段表示压应变逐渐增大，上升段表示压应变逐渐减小。3种因素中，上部自重和混凝土收缩徐变均使压应变增大，温度升高和降低则分别使压应变减小和增大。因此，曲线下降段经历季节性降温，3种因素均使压应变增大；曲线上升段，在经历季节性升温的同时压应变减小，说明升温引起的应变大于该时期弹性压缩和收缩徐变之和。此外，不同测点间存在应变差异，如S1测点从气温最低至气温最高期间应变变化约300×10–6，而相同时间段内W1测点应变变化200×10–6。

图7 第18层施工期应变发展

图8为第28层施工后四根外框角柱一年内的应变–时程曲线，主要分为三个阶段。南区S1测点和北区N1测点之间的最大应变差异为200×10–6左右。对比第18层S1测点和第28层的S1测点，第18层S1测点压应变从2018年1月—2018年7月（冬—夏）减小了290×10–6，而第28层S1测点压应变从2018年7月—2019年1月（夏—冬）增大了530×10–6。将图7、8与图4、5对比可知，温度变化曲线与应变发展曲线具有较强相关性，季节性温度变化引起的结构应变大于收缩徐变和自重荷载引起的应变。施工期内不同楼层经历了不同的季节性温度变化，具有不同的应变变化规律。

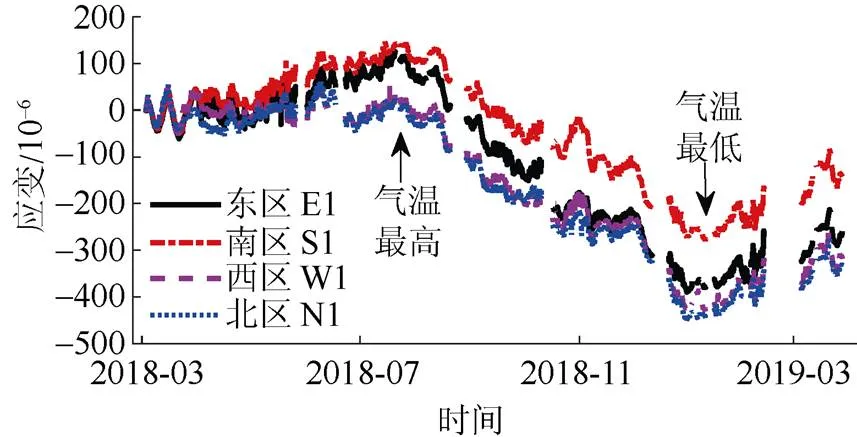
图8 第28层施工期应变发展

3 施工期主体结构竖向变形监测

结构的竖向荷载传递路径从上到下依次是楼板—梁—柱/墙—基础，结构的柱/墙受上部结构荷载和混凝土收缩徐变的共同作用，产生竖向变形。由于主体结构的外框–内筒的竖向刚度和所承受荷载存在差异，会产生内外竖向变形差。结构基础的不均匀沉降也会导致结构不同区域产生竖向变形差和附加应力，从而影响结构性能和安全。因此，需要对地面沉降、结构竖向变形以及外框–内筒竖向变形差进行监测，有利于控制结构标高和施工垂直度，提高施工质量。

结构施工过程中，每层楼的施工标高是楼层设计标高与标高补偿之和。标高补偿值根据JGJ 8—2016《建筑变形测量规范》[17]计算得出，先计算结构封顶后各层的竖向位移，然后确定各层标高差异和相应的补偿值。但结构实际变形与理论计算值存在差异，因此在施工期持续监测关键楼层的标高，可验证理论标高补偿值是否准确，作为调整标高的依据。

3.1 结构标高测量方法

长航大楼采用内外同步施工方案，第一层施工时间为2016年1月，至2018年12月，大楼施工至第57层。通过测量第1、5、10、15、20、25、30、35、40、45、50层的楼层标高相对于地面基准点的变化来计算第1层地面沉降和主体结构的竖向变形。从2017年7月25日—2018年12月26日，共进行8次测量，如表1所示。图9为每次竖向变形测量时对应的结构施工进度。

表1 竖向变形实际测量时间

每个观测层有12个测点，其中外框柱8个，核心筒4个，测点布置、标高测量方法以及测量仪器如图10所示。以施工高程控制点作为结构高程传递的基点，采用悬挂钢卷尺配合精密水准仪由下往上传递高程，计算标高时需对钢尺温度、尺带质量和尺带的张力进行修正。测点布置在被监测楼层的外框柱和核心筒墙体上。当被监测楼层的临时支撑脚手架拆除后，对该楼层进行标高监测，得到楼层标高随时间的变化。并在同一楼层采用闭合回路测量，监测同一层各测点标高变化差异，得到各测点的不均匀竖向变形。

图10 竖向变形测点布置、测量原理和测量仪器

图10（b）中1、1、2、2为水准仪观测到的读数，尺砣质量为5 kg，钢尺从下到上读数。第一层观测点高程为，第五层观测点的高程为，高程变化表示为：

Δ=(2–1)–(2–1) （1a）

=(2–1)–(2–1)+（1b）

式中：1和2需要根据实际监测时的环境温度、尺砣质量、1和2之间的长度等因素进行修正。为降低测量误差，进行三次测量取平均值。处理数据时，先将环境温度引起的钢卷尺温度变形进行扣除，从而得到结构真实的竖向标高变化。结构竖向变形测量所用仪器如图10（c）所示。采用徕卡TS60高精度全站仪测量不同楼层中固定测点的绝对和相对高程，测量精度0.5 mm。水准仪型号为FOIF-DSZ1，每公里往返测量高差中误差小于1.0 mm，用于高程传递测量。

3.2 竖向变形监测结果与分析

在分析主体结构自身的竖向变形之前，需要先分析地面沉降的影响。第1层的各个测点位于柱子或墙的底部，与地面平齐，因此第1层测点的标高变化表示主体结构的地面沉降。图11（a）显示了第1层各测点的地面沉降绝对值。以2017年7月25日第一次测量的标高作为初始值，随着施工进行，至2018年12月，结构第1层地面沉降从零逐渐增大到10 mm左右。图11（b）为第一层外框柱8个测点和核心筒4个测点的平均地面沉降，纵坐标负号表示沉降方向向下。由图可知：1）地面沉降与时间呈近似线性关系，2018年3月的测量值在拟合直线上方（实际沉降小于线性预测值）的原因是该阶段结构施工暂停了几个月，结构重量没有增加，沉降速度减缓；2）外框与核心筒两条线基本重合，可知第1层外框柱与核心筒之间的地面沉降基本相同。此外，还能计算出这期间基础的平均沉降速度为0.02 mm/d，该沉降速度在JGJ 8—2016《建筑变形测量规范》中规定的稳定沉降速率范围内（0.01～0.04 mm/d）。上述结果说明施工期主体结构地面均匀沉降，不会因地面不均匀沉降影响上部结构的标高测量，因此可忽略地面沉降对主体结构竖向变形的影响。

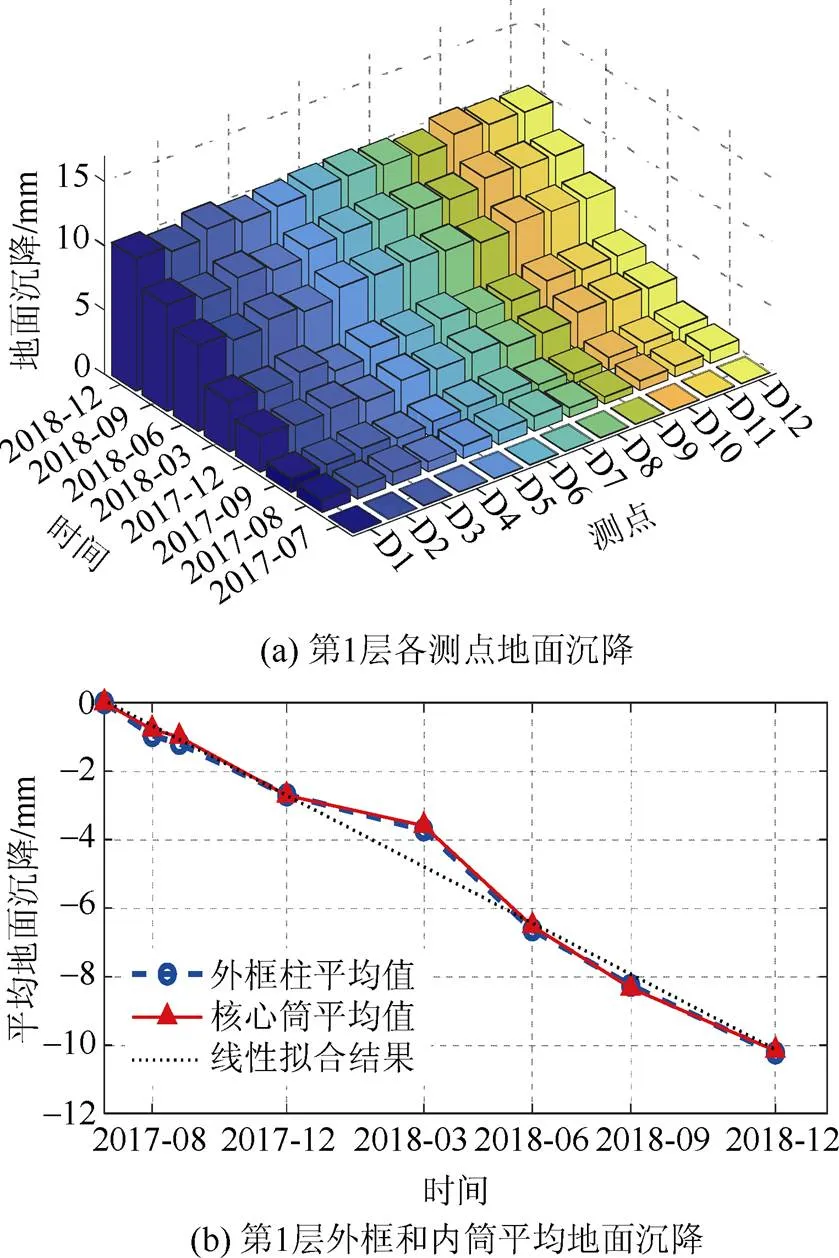
图11 第1层地面沉降

接着，研究主体结构前5层和前10层结构的施工期竖向变形。第5层首次测量时间为2017年7月25日，第10层首次测量时间为2017年8月31日。图12为前5层和前10层各测点的竖向变形随时间的累积。从2017年7月25日到2018年12月26日，前5层竖向变形从零逐渐增大至6 mm左右；从2017年7月25日到2018年9月5日，前10层竖向变形从零逐渐增大至13 mm左右。比较两图中同一层内各个测点之间的竖向变形值，可知不同测点之间存在一定的竖向变形差。将前5层和前10层外框测点和核心筒的测点分别取平均值，如图13所示。前5层的竖向变形从零逐渐增大至5 mm左右，前10层的竖向变形从零逐渐增大至11 mm左右。图中2017年12月至2018年3月期间竖向变形很小的原因是结构施工暂停，上部结构质量未发生变化。在内外变形差方面，前5层外框与核心筒的两条线基本重合，竖向变形差很小。前10层从2017年9月开始外框柱竖向变形稍大于核心筒，差异幅度在0.3 mm左右，占前10层总体竖向变形的2.7%。

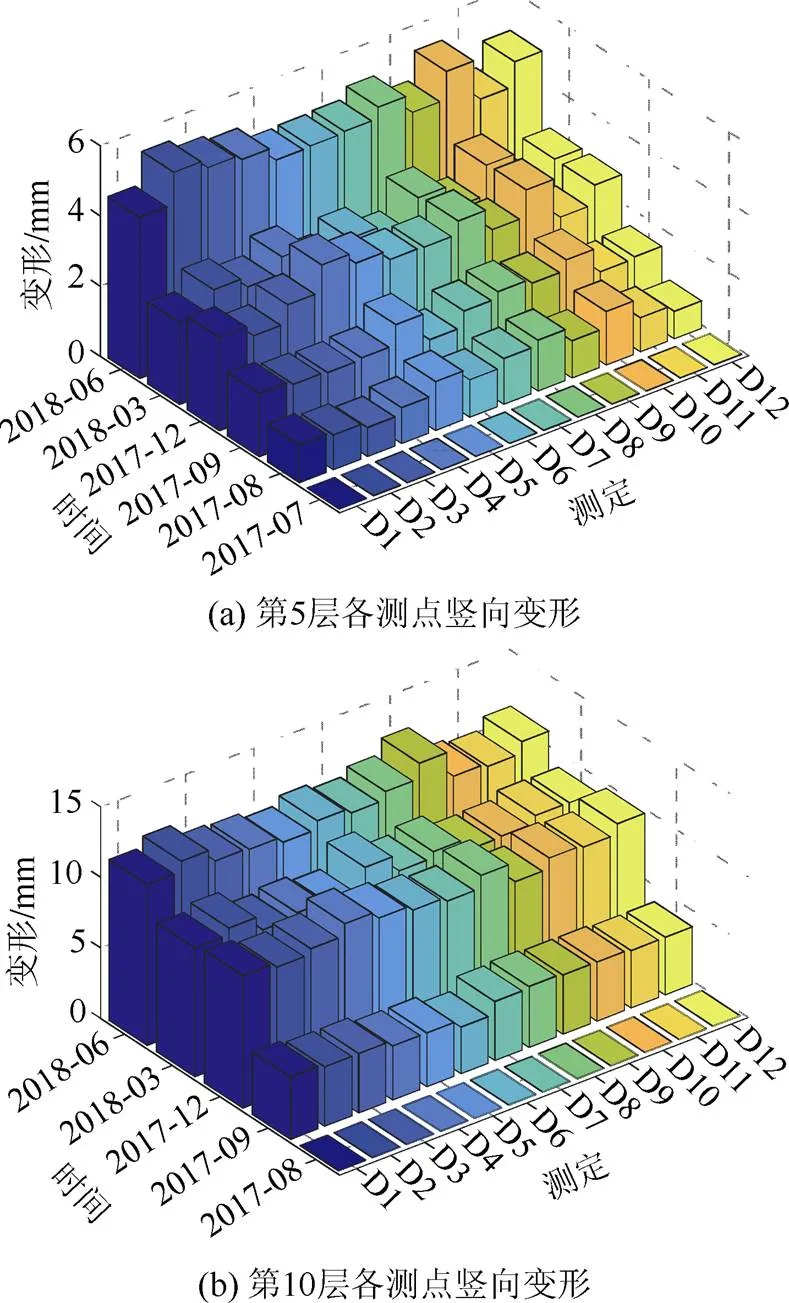
图12 第5层和第10层各测点竖向变形

图13 前5、10层外框柱与核心筒平均竖向变形

由于柱子和剪力墙会因为构件刚度差异、施工质量差异以及荷载分布不均等原因存在竖向变形差。长航大楼外框内筒同步施工且两者由主梁和楼板连为一整体，因此核心筒和外框柱所受上部荷载可视为均布荷载。以核心筒测点D11为相对基准点，计算其他测点相对于D11测点的标高变化，得到各测点之间的竖向变形差，如图14～图18所示。图中0轴黑色虚线表示初始状态，纵坐标为正表示该测点竖向变形小于基准点，为负则反之。

由图14可知，第5层各测点之间竖向变形差基本控制在1 mm以内，且D2～D8测点的变形值非常接近。各测点的竖向变形基本都为负值，说明第5层D11测点竖向变形最小。从第10层开始，各测点的层间竖向变形差相比之前变大，说明层间竖向变形的不均匀程度变大。

图14 第5层各测点相对竖向变形差

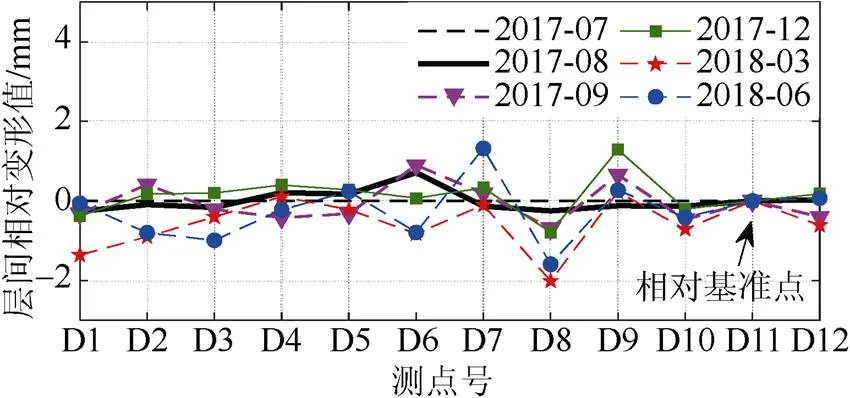
图15 第10层各测点相对竖向变形差

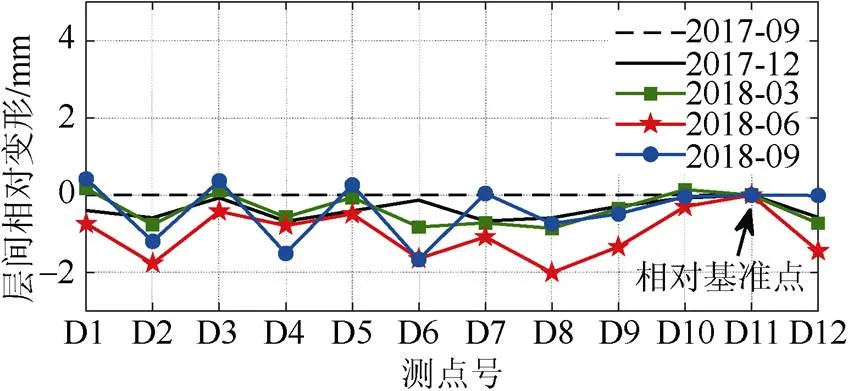
图16 第15层各测点相对竖向变形差

图17 第20层各测点相对竖向变形差

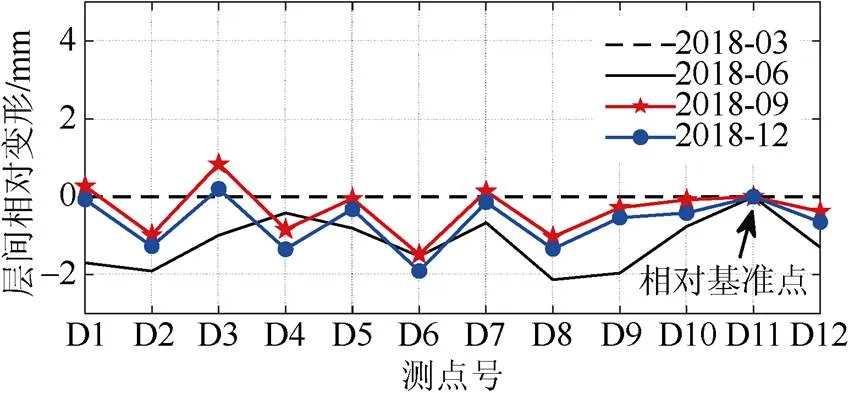
图18 第25层各测点相对竖向变形差

如图15～图18，第10层其他测点相对D11测点的最大差值为2 mm，各测点间最大差值为2.9 mm；第20层其他测点相对于D11的最大差值为3.2 mm，各测点间相对最大差值为5.3 mm（2018年12月曲线D1、D7两测点标高之差）；第15层和第25层的层间测点相对变形差小于2 mm。

计算每个监测层各个测点竖向变形差取绝对值的平均值，表示各测点竖向变形的不均匀程度，如图19所示。第1层测点的不均匀变形程度小于0.2 mm。第5～25层的层间不均匀竖向变形程度总体上随时间逐渐增大，也随结构高度而增大，但基本保持在1.5 mm范围内。

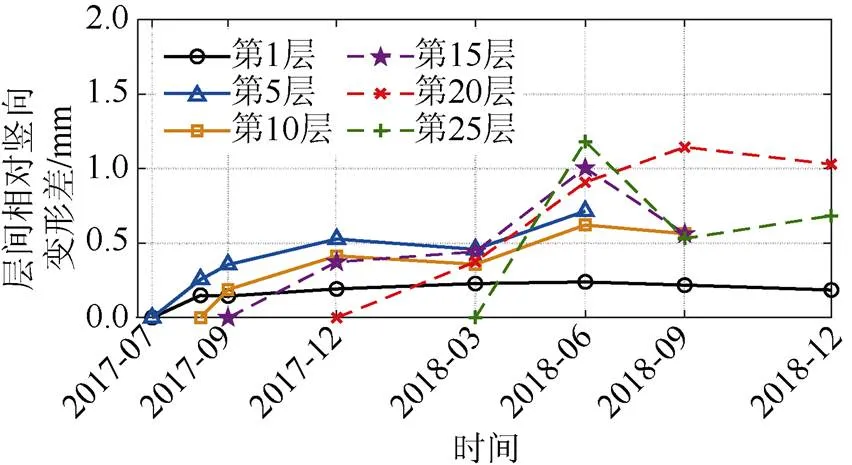
图19 各监测层的平均层间相对竖向变形差

主梁负责连接外框柱与核心筒，外框与核心筒之间的竖向变形差会引起主梁的轴向应力变化。图20为2018年2月—2018年7月期间第18层主梁两端外框柱与核心筒之间的竖向应变差，不同区域的内外竖向应变差异较大。内外竖向应变差会引起主梁剪切变形，主梁上表面产生轴向拉应力。图21为第18层主梁在2018年2月—2018年7月期间的轴向应力变化值，其中东区EI主梁的应力变化最大，拉应力增大了1.49 MPa。比较图20和图21可知，主梁的轴向应力变化与其两端的内外竖向应变差成正相关，竖向应变差越大，主梁轴向应力变化越大，可能存在受拉开裂风险。

图20 第18层主梁两端竖向应变差

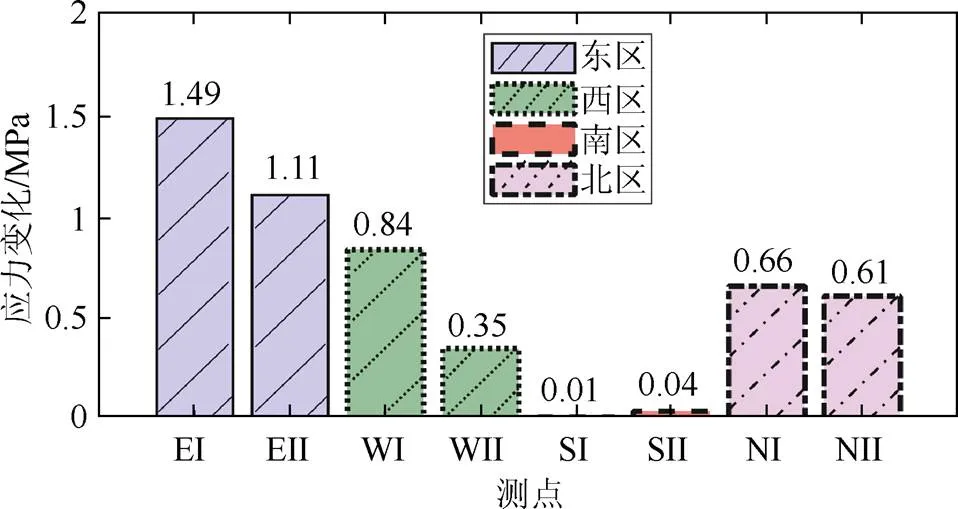
图21 第18层主梁的轴向应力变化

4 施工期结构水平动态位移监测

结构在施工期受到的动荷载分为环境激励和施工活荷载两类，其中环境激励包括地震动和风荷载，施工活荷载包括塔吊作业、施工电梯运行以及高压泵输送混凝土等等。动荷载引起结构水平向振动，使结构产生水平变形和水平加速度。

为了测量结构在施工阶段发生的动态位移，采用本人所在团队提出的一种适用于超高层建筑的结构动态位移估计方法进行长航大楼的施工期动态位移估计[18]。该方法基于卡尔曼滤波原理将应变数据与加速度数据融合得到高精度结构动态位移，其主要过程为：1）基于结构的几何变形原理，通过虚功原理和图乘法推导出结构局部应变与整体位移之间的应变–位移计算公式，通过分布式应变数据得到结构的应变–位移；2）建立结构位移的状态模型，并推导卡尔曼滤波预测和修正基本方程；3）通过加速度数据预测结构位移，计算预测误差，基于预测误差计算权重系数，最后将应变–位移和加速度–位移加权融合，提高结构动态位移的估计精度。

本文中，先进行长航大楼动态应变和加速度监测。动态应变计布置在结构的第1、5、11、16、25、35层，共6个楼层。在每个监测层，应变计对称布置在核心筒的外侧表面，测量核心筒的竖向动应变，拉应变为正，压应变为负。加速度计布置在主体结构第25层和第35层，测量该楼层的水平加速度。应变计与加速度计采用前文所述的BDI传感器，采样频率10 Hz，测点布置如图22所示。应变计最小分辨率为0.2×10–6，加速度计最小分辨率为0.001。

4.1 动态应变和加速度监测

图23（a）为施工荷载（该时间段内塔吊作业）作用下6个监测楼层的外框柱的动态应变，有动态施工荷载时结构动态应变幅值明显增大，振幅范围为±6×10–6。图23（b）为环境激励下不同楼层的动态应变响应，振幅范围为±3×10–6，应变幅度为施工荷载作用时的一半。

图24（a）为施工荷载作用下第35层水平加速度响应，响应范围是±1×10–3m/s2；图24（b）为环境激励下第35层水平加速度响应，响应范围是±5×10–4m/s2左右。对比两图可知，施工活荷载引起的结构动态响应最大幅值是环境激励下的2倍以上。通过快速傅里叶变换对动态数据进行处理识别结构频率，表2比较了基于第25和35这两个楼层的加速度和第25层动态应变的结构频率识别结果。其中，基于加速度数据识别出结构前两阶振动频率分别为0.230 7 Hz和0.759 3 Hz，基于应变识别的结构前两阶频率为0.228 3 Hz和0.760 5 Hz，前两阶频率识别结果差异分别为1.0%和0.2%。

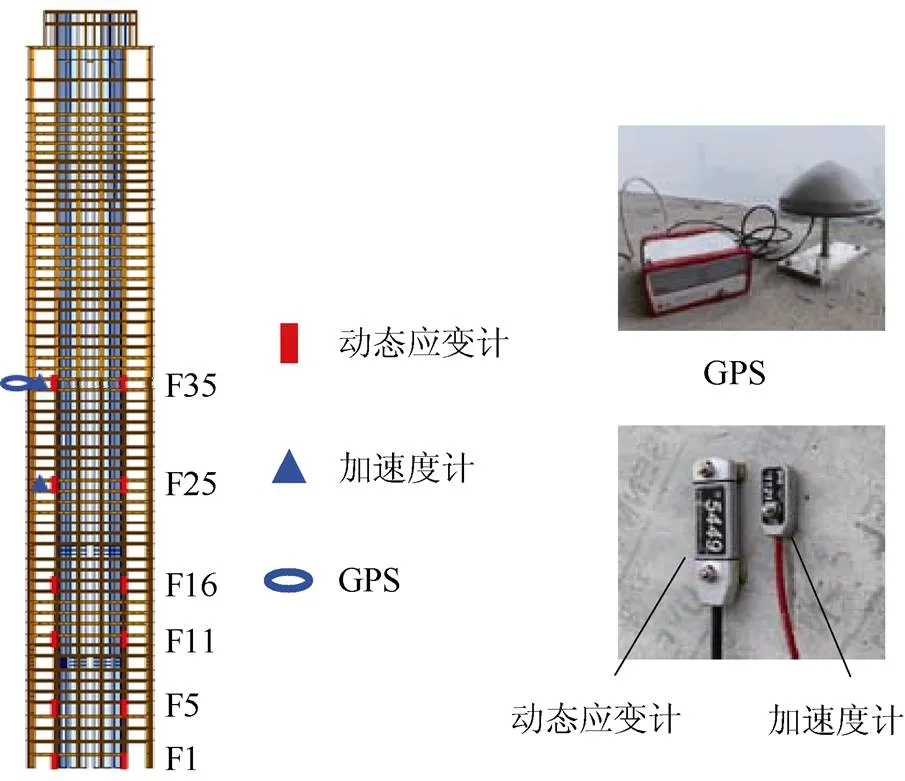
图22 结构动态响应传感器布置

图23 两种荷载下各楼层的动态应变响应

图24 两种荷载下下第35层水平加速度

表2 基于不同传感器数据的结构频率识别结果

4.2 水平动态位移估计

本文中，先基于应变–位移转换公式计算结构第35层的水平位移，然后与第35层加速度数据融合得到融合位移。图25比较了一段100 s时间窗口内的GPS所测位移和加速度–应变融合位移估计结果，融合位移曲线趋势与图23（a）中动态应变曲线前100 s的趋势基本一致，反映了结构在塔吊作业等施工荷载下发生的水平位移，最大水平位移在5 mm左右。相比之下，GPS位移曲线趋势与融合估计位移存在明显差异，这是由于施工期结构周围的爬模等临时支护结构遮挡了部分GPS卫星信号，使得GPS在测量动态位移时存在较大误差。

图25 施工荷载作用下第35层的水平动态位移

将融合位移与GPS位移进行快速傅里叶变换，识别结构的振动频率，如图26所示。基于融合位移识别出结构的两阶频率，分别为0.228 3 Hz和0.760 5 Hz。GPS位移在频域中未出现明显峰值，幅值最大处对应的频率为0.280 8 Hz。由于长航大楼在建造过程中未经历台风、地震等极端荷载作用，其动态位移量级较小，始终处于规范规定的安全范围内。

图26 基于位移的结构频率识别

5 结 论

本文基于实际超高层建筑的施工期健康监测系统，对超高层建筑主体结构的施工期竖向变形、温度变形和动态位移等静动态变形进行了实测研究，主要结论如下：

1）基于不同楼层不同区域的温度和应变数据，总结了施工期主体结构的温度不均匀分布规律，以及温度不均匀分布引起的结构应变差异，季节性温差引起的应变大于同时段内上部结构自重和混凝土收缩徐变引起的应变。

2）层间不均匀竖向变形程度随时间逐渐增大，也随结构高度而增大，前25层平均层间竖向变形差小于1.5 mm。主梁的轴向应力与其两端的外框柱与核心筒之间竖向应变差成正相关。

3）通过卡尔曼滤波融合超高层结构动态应变和加速度数据，能够准确估计结构动态位移并识别结构前两阶振动频率。

本文研究结果可为具有相似结构体系的超高层建筑施工期静态和动态变形监测提供有利参考，对于减小不均匀变形导致的施工误差等不利影响具有重要意义。

[1] 汪大绥, 包联进. 我国超高层建筑结构发展与展望[J]. 建筑结构, 2019, 49(19): 11–24.

[2] SU J Z, XIA Y, WENG S. Review on field monitoring of high-risestructures[J/OL]. Structural Control and Health Monitoring, 2020, 27(12). [2023-08-31]. https: //doi.org/10.1002/stc.2629.

[3] 王晓蓓, 高振锋, 伍小平, 等. 上海中心大厦结构长期竖向变形分析[J]. 建筑结构学报, 2015, 36(6): 108–116.

[4] GLISIC B, INAUDI D, LAU J M, et al. Ten-year monitoring of high-rise building columns using long-gauge fiber optic sensors[J/OL].Smart Materials and Structures, 2013, 22(5). [2023-08-31]. https: // iopscience.iop.org/article/10.1088/0964-1726/22/5/055030

[5] CHOI S W, KIM Y, KIM J M, et al. Field monitoring of columnshortenings in a high-rise building during construction[J]. Sensors, 2013, 13(11): 14321–14338.

[6] 中华人民共和国住房和城乡建设部. 高层建筑混凝土结构技术规程: JGJ 3—2010[S]. 北京: 中国建筑工业出版社, 2010.

[7] SU J Z, XIA Y, NI Y Q, et al. Field monitoring and numerical simulation of the thermal actions of a supertall structure[J/OL]. Structural Control and Health Monitoring, 2017, 24(4). [2023-08-31]. https: //doi.org/10.1002/stc.1900

[8] PIRNER M, FISCHER O. Long-time observation of wind and temperature effects on TV towers[J]. Journal of Wind Engineeringand Industrial Aerodynamics, 1999, 79(1–2): 1–9.

[9] BREUER P, CHMIELEWSKI T, GÓRSKI P, et al. The Stuttgart TV Tower: displacement of the top caused by the effects of sun and wind[J]. Engineering Structures, 2008, 30(10): 2771–2781.

[10] YU J, MENG X, YAN B, et al. Global Navigation Satellite System- based positioning technology for structural health monitoring: a review[J/OL]. Structural Control and Health Monitoring, 2019, 27(1). [2023-08-31]. https: //doi.org/10.1002/stc.2467

[11] ZHANG L, LIU P, YAN X, et al. Middle displacement monitoringof medium-small span bridges based on laser technology[J]. StructuralControl and Health Monitoring, 2020, 27(4). [2023-08-31]. https: // doi.org/10.1002/stc.2509

[12] LUO L, FENG M Q. Edge-enhanced matching for gradient-based computer vision displacement measurement[J]. Computer-Aided Civil and Infrastructure Engineering, 2018, 33(12): 1019–1040.

[13] JANG H L, HAN D H, HWANG M Y, et al. Displacement, strain and failure estimation for multi-material structure using the displacement-strain transformation matrix[J/OL]. Materials, 2020, 13(1). [2023- 08-30]. https: //doi.org/10.3390/ma13010190

[14] TEZCAN J, MARIN-ARTIEDA C C. Least Square Support Vector Machine based approach to obtain displacement frommeasured acceleration[J]. Advances in Engineering Software, 2018, 115: 357–362.

[15] GAO F, ZHOU H, LIANG H, et al. Structural deformation monitoring and numerical simulation of a supertall building during constru­ction stage[J]. Engineering Structures, 2020, 209. [2023-08-31]. https: //doi.org/10.1016/j.engstruct.2019.110033

[16] 朱宏平, 高珂, 翁顺, 等. 超高层建筑施工期温度效应监测与分析[J]. 土木工程学报, 2020, 53(11): 1–8.

[17] 中华人民共和国住房和城乡建设部. 建筑变形测量规范: JGJ 8—2016[S]. 北京: 中国建筑工业出版社, 2016.

[18] ZHU H P, GAO K, XIA Y, et al. Multi-rate data fusion for dynamic displacement measurement of beam-like supertall structuresusing acceleration and strain sensors[J]. Structural Health Monitoring, 2020, 19(2): 2520–2536.

Static and Dynamic Deformation Monitoring of Super High-Rise Buildings During the Construction Stage

GAO Ke1DENG Deyuan2ZHU Hongping1, 3WENG Shun1, 3GAO Fei1, 3

(1. School of Civil and Hydraulic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; 2. China Construction Steel Structure Guangdong Co., Ltd., Huizhou 516259, China; 3. Hubei Key Laboratory of Control Structure, Wuhan 430074, China)

To address the insufficient research on the measurement of static and dynamic deformations of super high- rise buildings during the construction stage, a structural health monitoring (SHM) system was installed on the main structure of a practical super high-rise building with a height of 335 m. Thus the temperature deformation, vertical deformation, and dynamic displacement of the main structure during the construction stage were measured and analyzed. The uneven distribution of temperature in the main structure during the construction stage was identified, and the strain characteristics of the structure under the influence of temperature were analyzed. The results showed that the strain caused by seasonal temperature difference was greater than the strain caused by the self-weight of the upper structure and the concrete shrinkage and creep over the same period. The developments of the vertical deformation and the inter-story uneven deformation during the construction stage were explained. The degree of uneven deformation increased with structural height and time. The maximum deformation difference among the points of the same floor was 5.3 mm. The axial stress of the girder was positive correlated with the difference in vertical strain between the twoends of the girder. The difference in vertical deformation between the outer frame and the core tube could lead to tensile cracking in the girder. A structural dynamic displacement estimation method based on Kalman filtering was proposed, which could improve could the accuracy of dynamic displacement estimation by fusing acceleration data and strain data, and could accurately estimate the dynamic displacement of super high-rise building under dynamic construction loads.

super high-rise building; structural health monitoring; temperature deformation; vertical deformation; dynamic displacement estimation

高珂, 邓德员, 朱宏平, 等. 超高层建筑施工期结构静动态变形监测[J]. 工业建筑, 2024, 54(1): 130-139. GAO K, DENG D Y, ZHU H P, et al. Static and Dynamic Deformation Monitoring of Super High-Rise Buildings During the Construction Stage[J].Industrial Construction, 2024, 54(1): 130-139 (in Chinese).

10.3724/j.gyjzG23081112

*国家重点研发计划项目（2021YFF501001）；国家自然科学基金（52308315，51838006）；中国博士后科学基金（2023M731206）；湖北省自然科学基金（2020CFA047）；华中科技大学交叉研究支持计划（2023JCYJ014）；中建钢构研发课题（CSCEC-PT-004-2022-KT-3.3）。

高珂，男，博士，助理研究员，从事结构健康监测和智能传感技术研究，gaoke06@hust.edu.cn。

翁顺，女，博士，教授，从事结构健康监测、损伤诊断和安全评估方法研究，wengshun@hust.edu.cn。

2023-08-11