基于卷积神经网络和交叉模型交叉模态方法的钢框架两阶段损伤识别研究

万 能 黄民水 朱宏平

基于卷积神经网络和交叉模型交叉模态方法的钢框架两阶段损伤识别研究

万 能1黄民水1朱宏平2

(1. 武汉工程大学土木工程与建筑学院，武汉 430073；2. 华中科技大学土木与水利工程学院，武汉 430074)

在结构损伤识别领域中，交叉模型交叉模态方法（CMCM）在求解含噪声的损伤识别问题时，受到系数矩阵不稳定的影响，往往导致损伤识别结果的精度下降。为了解决这一问题，提出了一种两阶段的损伤识别方法，旨在减少CMCM方法系数矩阵的冗余方程，提高CMCM方法的计算性能和噪声鲁棒性。首先，在第一阶段，通过卷积神经网络（CNN）进行结构损伤定位，以消除CMCM方法系数矩阵的冗余方程。其次，在第二阶段，求解已缩减的CMCM系数矩阵方程，得到更准确的损伤识别结果。通过数值和试验研究，验证了所提出的两阶段损伤识别方法的有效性，与传统的CMCM方法相比，所提方法在求解含噪声的损伤识别问题时，显著提高了损伤识别精度。

结构损伤识别；交叉模型交叉模态；卷积神经网络；两阶段方法

0 引 言

在土木工程领域，结构损伤识别（structural damage identification，SDI）作为结构健康监测（structural health monitoring，SHM）的重要组成部分，已成为维护结构安全的重要工具[1-2]。基于振动的结构损伤识别方法可分为基于数据与基于模型两大类，其中基于数据的方法涵盖机器学习等[3-4]，使用机器学习算法如深度学习来进行分析，无需建立有限元模型；基于模型的方法则包括基于模型修正的损伤识别等[5-6]，根据实验模态分析结果对比有限元模型进行损伤识别。

交叉模型交叉模态（cross model cross mode，CMCM）方法是基于模型修正的损伤识别方法之一，它无需对模态振型进行配对和迭代计算，即可直接修正或识别刚度矩阵和质量矩阵[7]。然而，该方法对于模态空间的完整性具有一定要求。Li等[8]利用模态缩聚和扩阶基于空间不完备信息进行损伤识别。贾辉等[9]提出了一种单元刚度矩阵优化储存方法，利用CMCM进行构损伤识别。占超等[10]提出将CMCM系数矩阵最小奇异值对应的右奇异向量作为损伤指示向量，避免了错误或不准确的假设给损伤识别结果带来的误差。王炎等[11]将CMCM拓展到随机领域，结合混合摄动–伽辽金方法提高CMCM的修正精度。Cong[12]将频响函数的极点和零点应用到CMCM中，同时修正结构的刚度、质量和阻尼矩阵。

以上研究证明了CMCM方法在结构损伤识别上的有效性，然而针对该方法在强噪的病态环境下的研究略显不足。本质上，CMCM方法旨在求解线性方程组，在噪声影响下，CMCM方程系数矩阵不稳定，会出现无实际意义的解。因此，Xu等[13]提出模态子集选择方法，消除了CMCM法中一些冗余方程，在实际结构中仅验证了结构的单损伤工况；Liu等[14]通过改变系数矩阵的形式，增加更多独立方程，来解决秩亏问题，但噪声鲁棒性较差。

针对以上问题，考虑到卷积神经网络（convolutional neural network，CNN）的强大局部特征提取能力和高效的识别分类功能[15]，其可作为损伤识别的前处理步骤。本研究提出了一种基于CNN和CMCM的两阶段结构损伤识别方法，旨在通过CNN识别潜在损伤位置，进一步消除CMCM方法中系数矩阵的冗余方程。通过美国土木工程师协会（ASCE）的Benchmark模型和三层框架的试验结构来验证所提方法的有效性及对噪声的鲁棒性。

1 理 论

1.1 卷积神经网络

随着人工智能快速发展，高效的机器学习模型已在土木工程领域占据重要地位。深度学习作为一种强大的人工智能框架为土木工程损伤识别提供了新的可能性。CNN是深度学习的代表性方法之一，相比于传统神经网络，它通过局部连接、权值共享和下采样等方式大大减少了参数数量，提高了计算效率。CNN主要由卷积层、池化层、全连接层组成，可以有效降低网络参数，防止过度拟合，提高局部特征提取效率。

卷积层是CNN的核心，通过将每个神经元的输入连接到前一层的局部感知区域来实现局部特征提取。池化层是特征映射层，它降低了卷积层的输出维度，实现了局部信息的下采样，有效防止了过拟合。最大池化是常见的池化方法之一，本文采用最大池化来表达局部特征，并采用多个卷积和池化层来实现特征提取。在全连接层中，每个神经元与前一层的所有神经元连接，通过层间权重系数的加权求和计算预测值。为了提高模型的表达能力，对全连接层和输出层分别采用ReLU和线性激活函数。本文采用的CNN结构如图1所示。

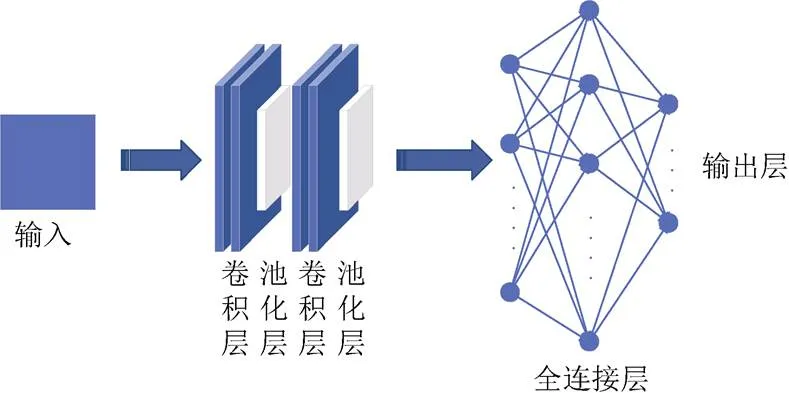
图1 CNN结构

1.2 交叉模型交叉模态

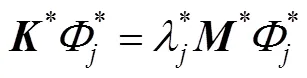
结构的刚度、质量矩阵关系为：

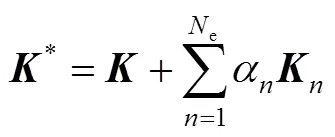
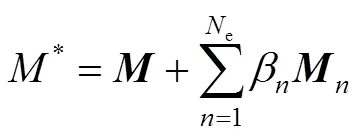
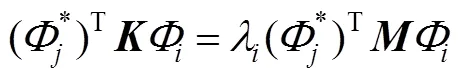
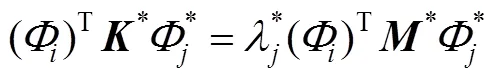
用式（3b）除以式（3a）的转置：

然后将式（2）代入式（4）中，整理后有：

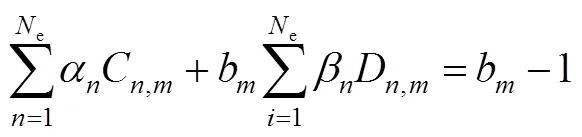
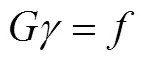
若结构质量不变，则CMCM方程简化为：

求解方程式（7）一般采用L1正则化[16]或L2正则化[17]。基于第一阶段CNN的定位结果，识别潜在损伤单元，可判断结构的损伤稀疏性，选择正确的正则化方式，提高CMCM方程的求解精度：当结构的损伤或者刚度变化往往发生在较少的单元或区域，使用L1正则化求解。

1.3 基于CNN与CMCM的两阶段损伤识别方法

为了解决CMCM方程的系数矩阵不稳定导致计算结果不准确的问题及提高在噪声影响下的鲁棒性，提出了一种基于CNN和CMCM的两阶段损伤识别方法，该研究方法步骤如下：

1）采用CNN构建振型与相应损伤位置的映射关系：将振型数据输入到CNN中，利用多重卷积和池化操作实现特征提取，并将其展开输入到全连接层，通过回归层映射到结构损伤。

2）将测量的实际振型输入到已训练好的CNN中，识别潜在损伤位置。

3）基于前一阶段的损伤定位结果，确定结构损伤稀疏性，选择合适的正则化方法求解已缩减的CMCM系数矩阵方程，准确计算结构损伤程度，并通过数值和试验研究验证所提方案的有效性。

研究方法的流程如图2所示。

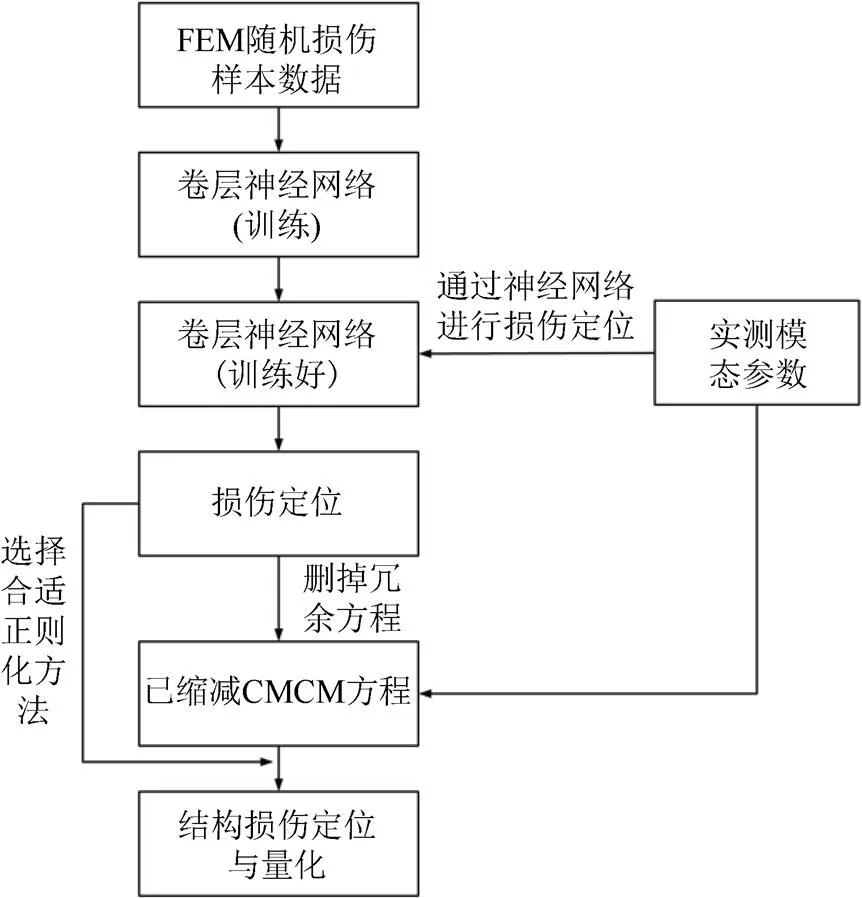
图2 两阶段方法流程

2 数值算例

通过ASCE的Benchmark模型进行数值算例研究，以证明所提方法的有效性。将采用CNN和传统CMCM分别进行损伤识别，并与所提出的两阶段方法进行对比。

该结构是一个4层的2跨×2跨钢框架模型，平面尺寸为2.5 m×2.5 m，每层层高为0.9 m。每层包含9根柱、12根梁和8根对角斜撑，柱、梁和对角支撑截面分别为B100×9、S75×11和L25×25×3（标称屈服强度300 MPa）[18]。基于MATLAB的数值模型和单元编号如图3所示。

图3 ASCE基准模型

2.1 样本数据生成

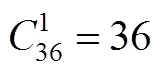
为考虑实际工程中的噪声影响，同阶振型的噪声相同，不同阶振型的噪声相互独立。通过在振型数据中添加随机变量，对测量噪声进行仿真，以验证所提方法的鲁棒性：

2.2 CNN性能评估

CNN输入的数据由前四阶的振型数据组成，数据维度为120×4，输出为结构损伤单元编号，数据维度为1×36。数据集随机分为三个部分：80%的数据用于训练，10%的数据用于验证，10%的数据用于测试。基于验证损失，逐步叠加各结构层并调整网络参数，训练曲线如图4所示。

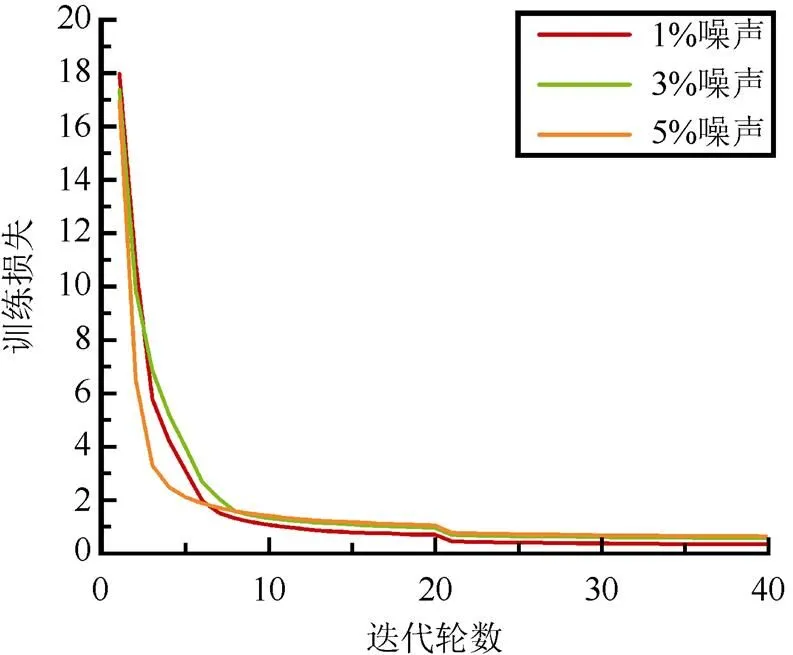
图4 ASCE基准框架的训练曲线

利用训练数据集和验证数据集的损失值及测试集的回归值（，0≤≤1）来定量评估训练好的模型性能。综上所述，损失值越小，越大，训练得到的模型精度越高。

表1 CNN性能评估结果

由表1可知，随着噪声水平的增加，性能会略微下降，仍能保证良好的模型精度。因此，基于特征向量训练的CNN模型可以提供准确损伤单元位置。

2.3 CNN损伤定位

利用表2所示的三个损伤工况展示训练好的CNN损伤定位性能，损伤定位结果如表2所示。

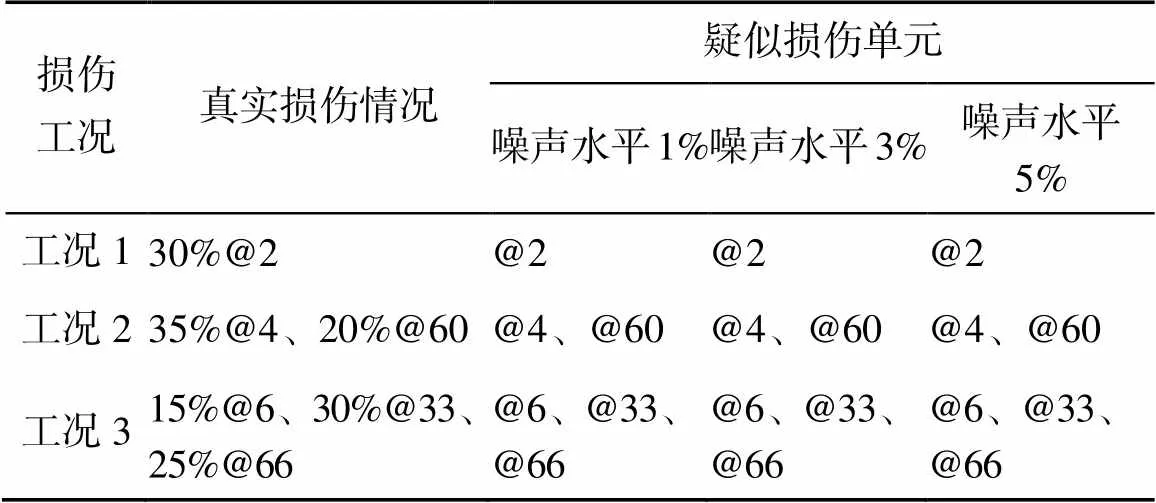
表2 损伤定位结果

2.4 CMCM损伤定量

通过第一阶段的CNN对结构损伤单元进行定位后，知悉损伤单元数远小于结构单元数，减少了CMCM系数方程的冗余方程，再利用L1正则化求解已缩减的CMCM系数矩阵方程，得到损伤识别结果。为进一步验证所提出方法的优势，将所提出的两阶段识别方法（方法1）分别与单独使用CNN（方法2）及单独使用CMCM（方法3）进行对比。针对三种损伤工况，损伤对比结果见图5～7。

根据对比结果看出，在噪声影响下，方法1在所有损伤工况下均能准确识别实际损伤，最大误差为2.1%；方法2损伤识别效果随着损伤单元和噪声水平增加而降低，最大误差为19.7%；而方法3，即传统的CMCM方法在求解含噪声损伤识别问题时，系数矩阵不稳定会导致线性方程组出现无实际意义的解。因此，所提出的两阶段损伤识别方法具有更高的准确性和鲁棒性。

图5 噪声1%损伤识别结果对比

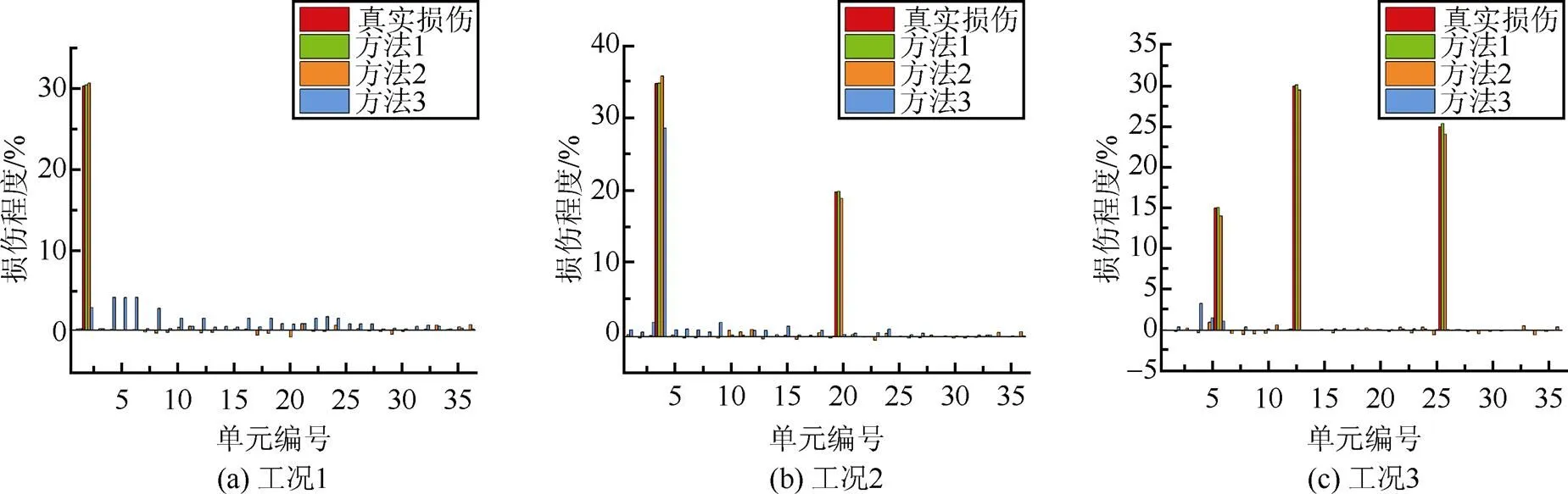
图6 噪声3%损伤识别结果对比

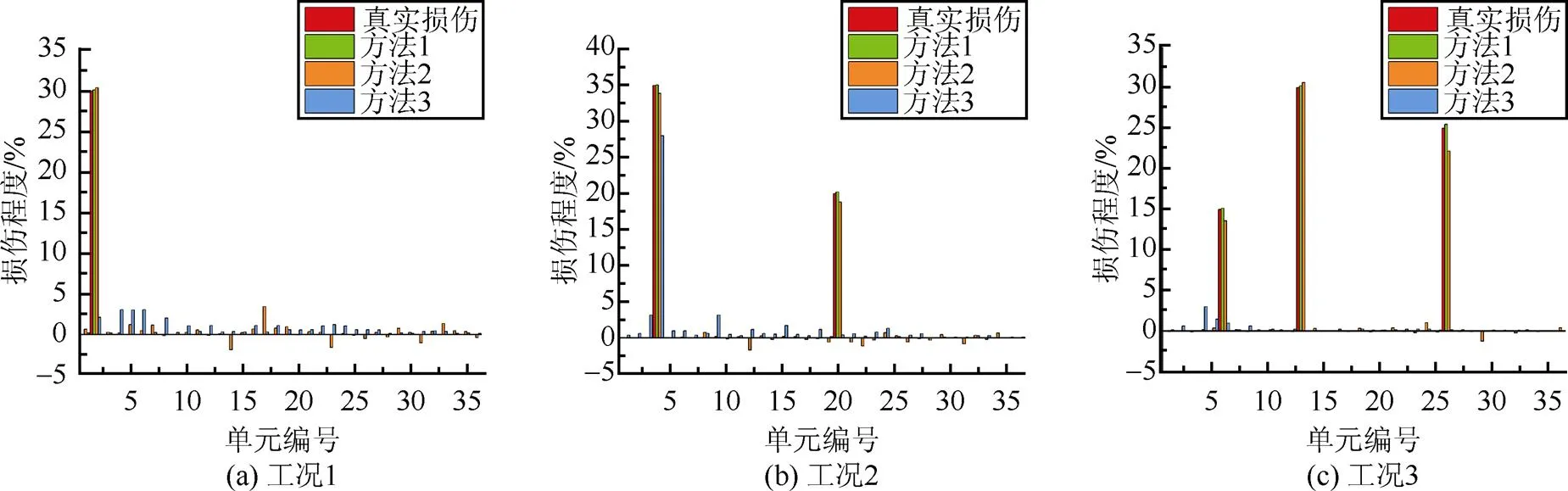
图7 噪声5%损伤识别结果对比

3 物理试验

为了通过真实数据验证本文所提出CNN与CMCM结合的损伤识别方法的适用性，采用如图8所示的三层框架结构作为试验结构[19]，验证所提算法的适用性。结构振动测试详情及物理参数可参考文献[19]。该结构由铝角柱和不锈钢钢板组成，它们通过铝支架连接。每个钢板的横向刚度可以独立改变，而不会永久损坏结构，这是通过用支架轻松更换柱子来实现的。不锈钢板的厚度和尺寸分别为4.0 mm和650 mm×650 mm。每层楼的柱高为0.7 m，其末端用两个螺栓固定在铝支架上。铝角柱的厚度和尺寸分别为4.5 mm 和30 mm×30 mm，每个用两个螺栓固定在板上。该结构安装在20 mm胶合板上，并用10 mm螺栓固定在振动台上。将厚度为4.5 mm的铝角柱更换为更薄的3.0 mm，以此引入损坏。传感器测点如图8所示。

3.1 模型修正

建立该框架结构的有限元模型，基于无损状态下测得的固有频率和振型，对结构单元刚度进行修正，以获得精确的有限元模型。图9中展示了试验和有限元模型无损状态下的振型。表3列出了试验和有限元模型的频率和MAC的修正结果，由表3可知，修正后的频率与实测频率之间的最大误差仅为0.05%，且MAC值均大于0.99，表明有限元模型与试验模型具有较好的相关性。因此，可以将修正后的有限元模型确定为基准有限元模型。

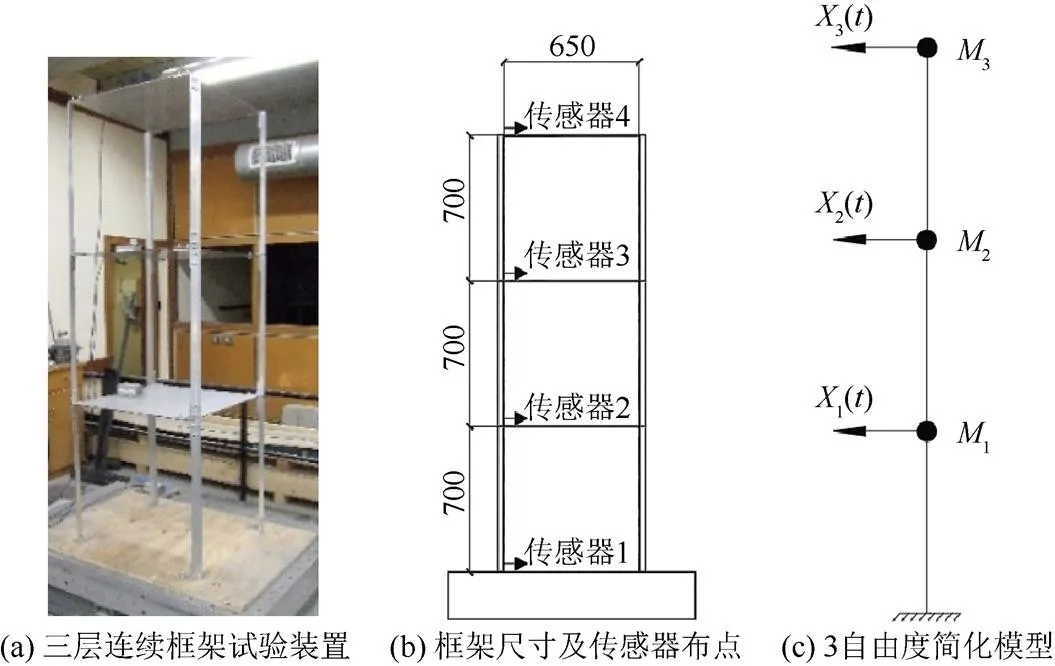
图8 三层连续框架结构及简化后3自由度体 mm

3.2 损伤定位

根据物理试验工况，对于结构的单工况和双工况损伤情况，单损和双损分别随机生成30 000个数据集。刚度折减系数随机取值，范围为[0，0.8]。

将损伤后的振型输入到CNN进行特征学习，输出结构损伤位置。此外，用于训练网络的数据拆分比例、网络架构和超参数与3.1节相同。由图10可知，该曲线具有良好的收敛性能，最终测试损失值为0.014。

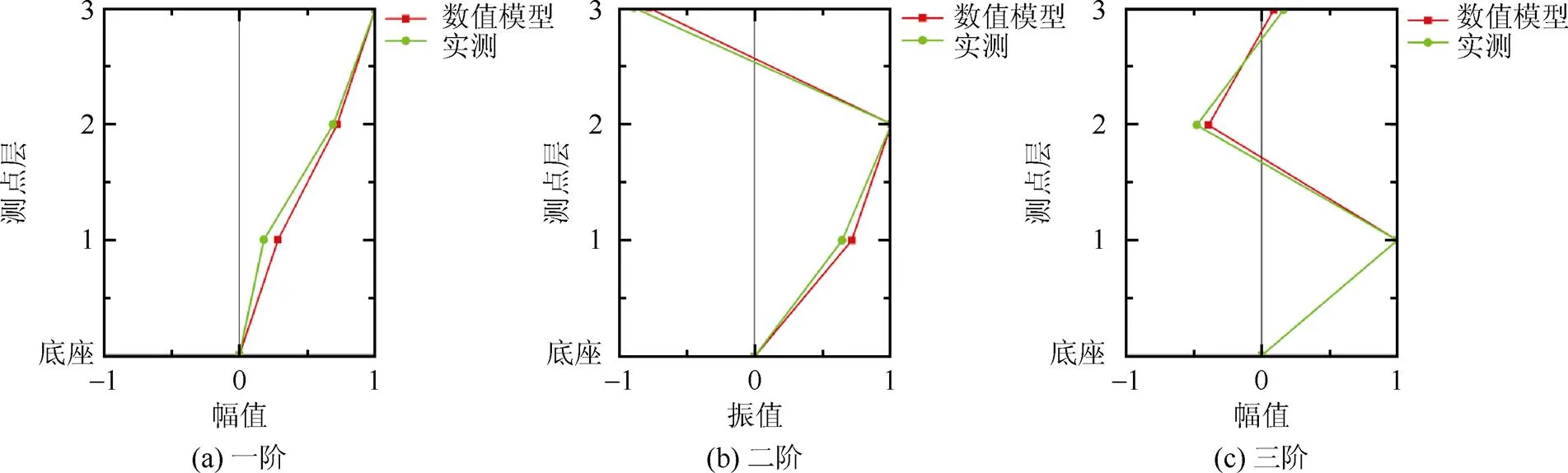
图9 无损状态下数值模型和实测的振型数据

表3 试验模型和数值模型的频率及MAC值

在实验室测试以下3种损伤工况进行验证：工况1，第一层刚度折减7%；工况2，第二层刚度折减10%；工况3，第一层刚度折减7%，第二层刚度折减10%。将实测的振型数据输入到已训练好的CNN中，3种工况均能准确识别损伤单元位置。

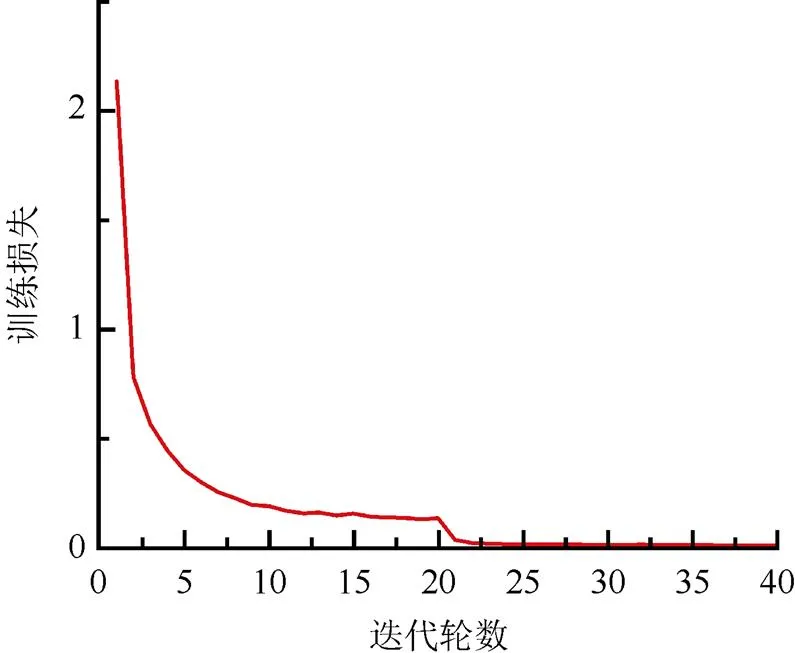
图10 三层连续框架结构的训练曲线

3.3 损伤定量

通过CNN识别结构潜在的损伤单元，进一步消除CMCM算法中系数矩阵的冗余方程，进行定量计算，平均损伤识别结果及相应误差如图11所示。

图11 三层框架结构的损伤识别结果及误差

从图11可以看出，基于CNN和CMCM的两阶段损伤识别方法，在单损与多损的情况下损伤识别的最大误差均不超过4%；传统CMCM方法，在单损与多损的情况下损伤识别的最大误差为12.8%。综上，三种损伤工况的试验验证表明所提方法在实际结构中的准确性及适用性。

4 结 论

通过研究ASCE的Benchmark框架模型和一个三层试验框架，验证了所提方法的有效性和准确性，并得出如下结论：

1）基于以上框架模型的研究，结果表明了所提出的两阶段损伤识别方法在5%的噪声下，针对多损伤单元，损伤识别的最大误差为2.1%，且可以应用于实际框架结构中。

2）所提出的两阶段研究方法基于传统的CMCM引入CNN，通过CNN识别损伤单元位置，确定损伤单元稀疏性，选择合适的正则化方法求解已缩减CMCM方程，解决了CMCM方法在噪声影响下的不适用性问题，提高了CMCM方法的损伤精度。

3）所提出的两阶段研究方法结合了CNN和CMCM算法的优点，能准确识别损伤，并提高了对噪声的鲁棒性，可解决实际工程中因环境噪声引起损伤识别结果不准确的问题。

[1] 周奎, 王琦, 刘卫东, 等. 土木工程结构健康监测的研究进展综述[J]. 工业建筑, 2009, 39(3): 96–102.

[2] GATTI M. Structural health monitoring of an operational bridge: a case study[J]. Engineering Structures, 2019, 195: 200–209.

[3] 温利明, 黄奕辉. 神经网络用于结构损伤识别的几个关键问题研究[J]. 工业建筑, 2002, 32(8): 39–40, 49.

[4] 顾箭峰, 向春燕, 陶甫先, 等. 基于深度学习和IHPO的桥梁结构模型修正方法[J]. 广西大学学报(自然科学版), 2022, 47(05): 1147–1159.

[5] 翁顺, 朱宏平. 基于有限元模型修正的土木结构损伤识别方法[J]. 工程力学, 2021, 38(3): 1–16.

[6] 雷勇志, 黄民水, 顾箭峰, 等. 环境温度影响下基于支持向量机与强化飞蛾扑火优化算法的结构稀疏损伤识别[J]. 计算力学学报, 2022, 39(2): 170–177.

[7] HU S L J, LI H, WANG S. Cross-model cross-mode method for model updating[J]. Mechanical Systems and Signal Processing, 2007, 21(4): 1690–1703.

[8] LI H, WANG J, HU S L J. Using incomplete modal data for damage detection in offshore jacket structures[J]. Ocean Engineering, 2008, 35(17/18): 1793–1799.

[9] 贾辉. 基于改进交叉模型交叉模态法的损伤识别研究[D]. 大连: 大连理工大学, 2011.

[10] 占超, 李东升, 任亮, 等. 基于改进交叉模型交叉模态法的局部损伤识别方法[J]. 振动与冲击, 2015, 34(7): 127–133.

[11] 王炎, 陈辉, 黄斌, 等. 利用改进交叉模型交叉模态的随机模型修正方法[J]. 振动工程学报, 2023, 36(2): 498–506.

[12] CONG S, HU S L J, LI H J. FRF-based pole-zero method for finite element model updating[J/OL]. Mechanical Systems and Signal Processing, 2022, 177[2022-05-05]. https://doi.org/10. 1016/j.ymssp. 2022.109206.

[13] XU M, WANG S, JIANG Y. Structural damage identification by a cross modal energy sensitivity based mode subset selection strategy[J/OL]. Marine Structures, 2021, 77[2021-02-24]. https:// doi.org/10.1016/j.marstruc.2021.102968

[14] LIU K, YAN R J, SOARES C G. An improved model updating technique based on modal data[J]. Ocean Engineering, 2018, 154: 277–287.

[15] LE C Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436–444.

[16] ZHOU X Q, XIA Y, WENG S. L1 regularization approach to structural damage detection using frequency data[J]. Structural Health Monitoring, 2015, 14(6): 571–582.

[17] TIKHONOV A N, ARSENIN V Y. Solutions of ill-posed problems[M]. Preston: Winston Press, 1977.

[18] JOHNSON E A, LAM H F, KATAFYGIOTIS L S, et al. Phase I IASC-ASCE structural health monitoring benchmark problem using simulated data[J]. Journal of engineering mechanics, 2004, 130(1): 3–15.

[19] OMENZETTER P, LAUTOUR O R D. Detection of Seismic Damage in Buildings Using Structural Responses: UNI/535[R]. Wellington: Earthquake Commission of New Zealand, 2008.

Research on Two-Stage Damage Identification of Steel Frame Based on CNN and CMCM

WAN Neng1HUANG Minshui1ZHU Hongping2

(1. School of Civil Engineering and Architecture, Wuhan Institute of Technology, Wuhan 430073, China; 2. School of Civil and Hydraulic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

In the field of structural damage identification, the Cross Model Cross Mode (CMCM) Method is constrained by the rank deficiency of the coefficient matrix when solving noise-inclusive damage identification problems, leading to a decrease in the accuracy of damage identification results. To address this issue, this study proposes a two-stage damage identification method aimed at reducing the redundant equations in the CMCM method’s coefficient matrix, thereby enhancing the computational performance and noise robustness of the CMCM method. In the first stage, a Convolutional Neural Network (CNN) is employed for structural damage localization to eliminate the redundant equations in the coefficient matrix of the CMCM method. Subsequently, in the second stage, the reduced CMCM coefficient matrix equation is solved to obtain more accurate damage identification results. The effectiveness of the proposed two-stage damage identification method is validated through numerical and experimental studies. Compared with the traditional CMCM method, the method proposed in this paper significantly improves the accuracy of damage identification in solving noise-inclusive damage identification problems, demonstrating its superior performance.

structural damage identification; CMCM; CNN; a two-stage method

万能, 黄民水, 朱宏平. 基于卷积神经网络和交叉模型交叉模态方法的钢框架两阶段损伤识别研究[J]. 工业建筑, 2024, 54(1): 123-129. WAN N, HUANG M S, ZHU H P. Research on Two-Stage Damage Identification of Steel Frame Based on CNN and CMCM[J]. Industrial Construction, 2024, 54(1): 123-129 (in Chinese).

10.3724/j.gyjzG23072612

*国家自然科学基金项目（52178300）。

万能，硕士研究生，主要从事结构健康监测研究。

黄民水，博士，教授，主要从事结构健康监测研究，huangminshui@tsignhua.org.cn。

2023-07-26